人教版数学八年级上册 13.3.1等腰三角形(二)课件(共13张PPT)
文档属性
| 名称 | 人教版数学八年级上册 13.3.1等腰三角形(二)课件(共13张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 461.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-15 19:33:30 | ||
图片预览

文档简介
(共14张PPT)
13.3.1等腰三角形(二)
等腰三角形有哪些什么性质?
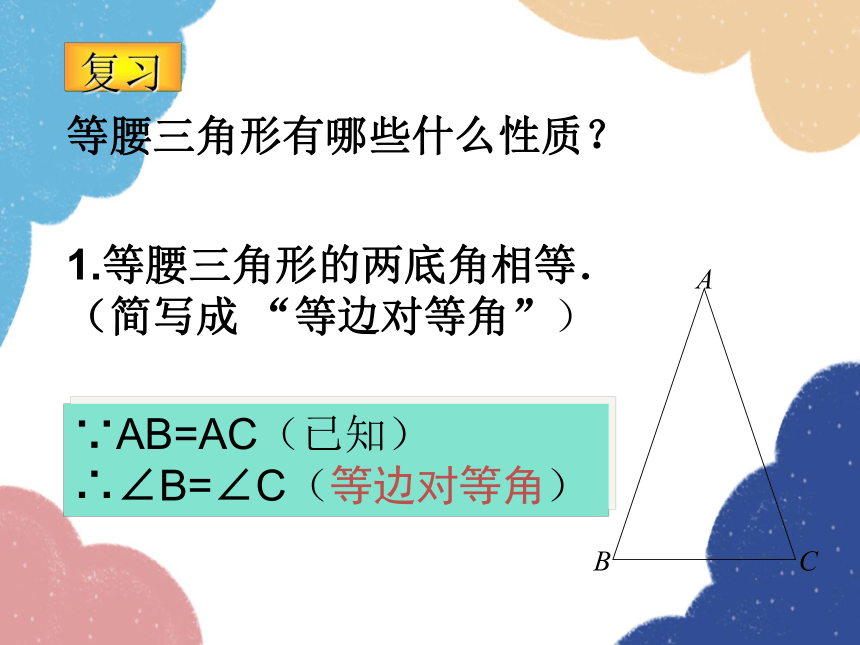
1.等腰三角形的两底角相等.
(简写成 “等边对等角”)
A
B
C
∵AB=AC(已知)
∴∠B=∠C(等边对等角)
复习
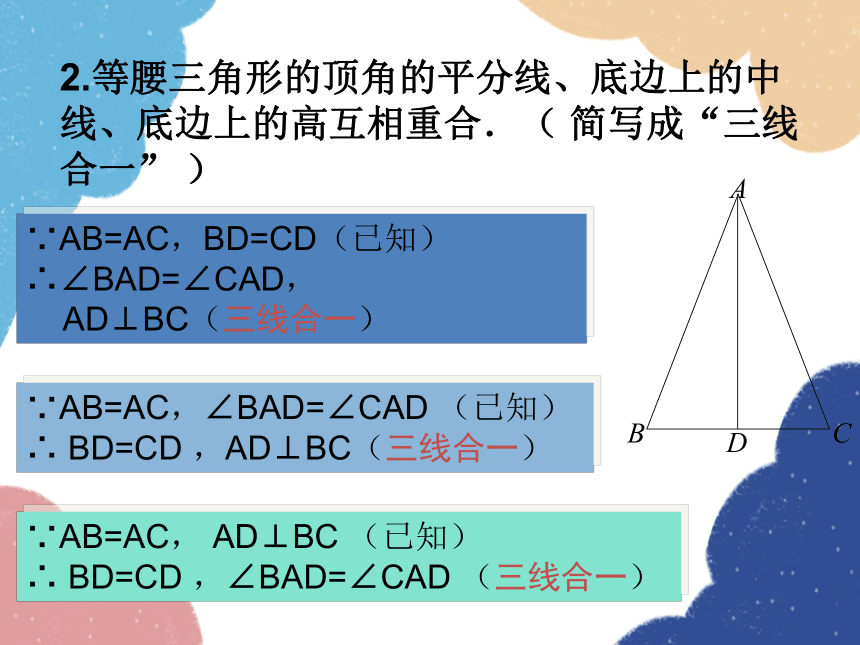
2.等腰三角形的顶角的平分线、底边上的中线、底边上的高互相重合.( 简写成“三线合一” )
A
B
C
D
∵AB=AC,BD=CD(已知)
∴∠BAD=∠CAD,
AD⊥BC(三线合一)
∵AB=AC,∠BAD=∠CAD (已知)
∴ BD=CD ,AD⊥BC(三线合一)
∵AB=AC, AD⊥BC (已知)
∴ BD=CD ,∠BAD=∠CAD (三线合一)
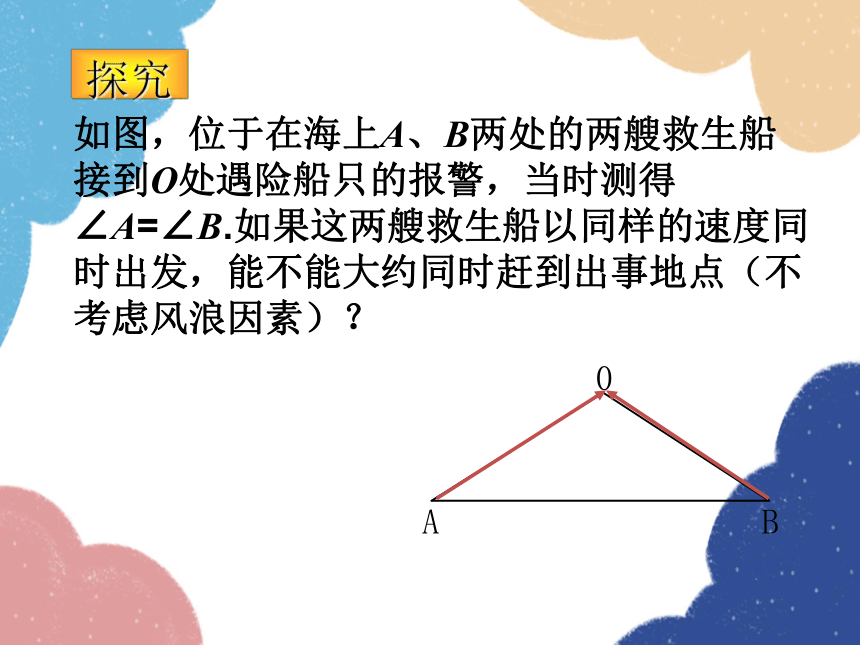
如图,位于在海上A、B两处的两艘救生船接到O处遇险船只的报警,当时测得∠A=∠B.如果这两艘救生船以同样的速度同时出发,能不能大约同时赶到出事地点(不考虑风浪因素)?
探究
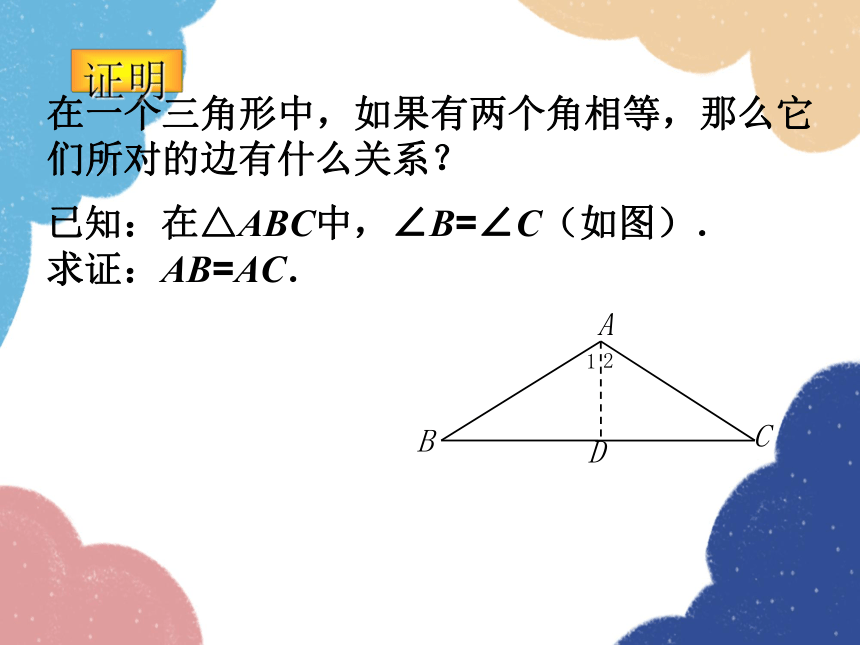
在一个三角形中,如果有两个角相等,那么它们所对的边有什么关系?
已知:在△ABC中,∠B=∠C(如图).
求证:AB=AC.
2
1
D
C
A
B
证明
C
A
B
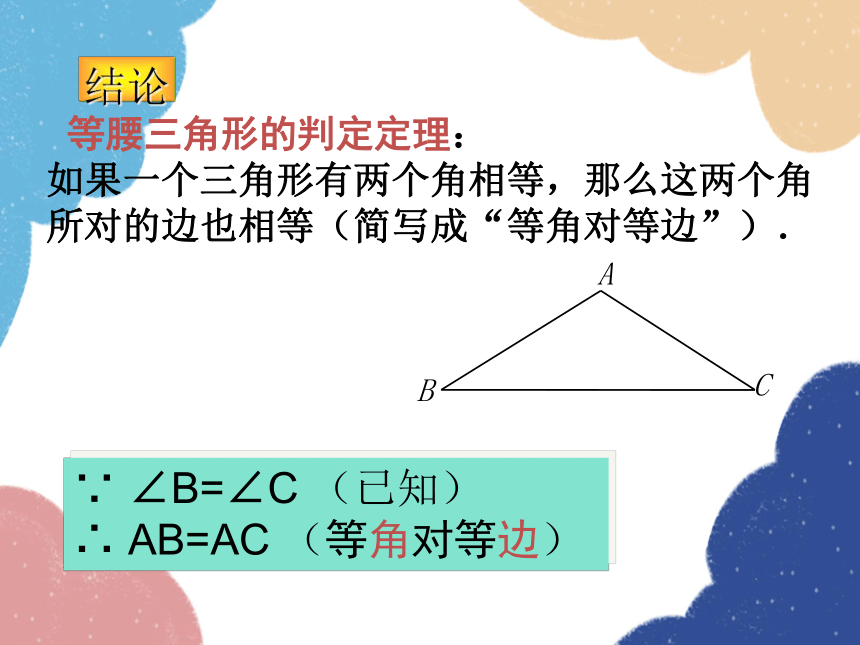
等腰三角形的判定定理:
如果一个三角形有两个角相等,那么这两个角所对的边也相等(简写成“等角对等边”).
结论
∵ ∠B=∠C (已知)
∴ AB=AC (等角对等边)
[例2]求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形.
已知: 如图, ∠CAE是△ABC的外角,∠1=∠2,AD∥BC.
求证:AB=AC.
应用
证明:∵AD∥BC,
∴∠1=∠B(两直线平行,同位角相等),
∠2=∠C(两直线平行,内错角相等).
又∵∠1=∠2,
∴∠B=∠C,
∴AB=AC(等角对等边).
角等
边等
判定
归纳
已知:如图,AD∥BC,BD平分∠ABC.
求证:AB=AD.
应用
例3 已知等腰三角形底边长为a,底边上的高的长为h,求作这个等腰三角形。
作法:1,作线段AB=a
2,作线段AB的垂直平分线MN,
与AB相交于点D。
3,在MN上取一点C,使DC=h.
4,连接AC,BC,则△ABC即为所求。
a
h
c
A
B
D
N
M
思考:在△ABC中,已知 ,BO平分∠ABC,CO平分∠ACB.
(1)请问图中有多少个等腰三角形 说明理由.
(2)线段EF和线段EB,FC之间有没有关系 若有是什么关系
AB=AC
AB≠AC
B
0
C
A
E
F
过点O作直线EF//BC交AB于E,交AC于F.
这节课你学到了什么
同学们再见
13.3.1等腰三角形(二)
等腰三角形有哪些什么性质?
1.等腰三角形的两底角相等.
(简写成 “等边对等角”)
A
B
C
∵AB=AC(已知)
∴∠B=∠C(等边对等角)
复习
2.等腰三角形的顶角的平分线、底边上的中线、底边上的高互相重合.( 简写成“三线合一” )
A
B
C
D
∵AB=AC,BD=CD(已知)
∴∠BAD=∠CAD,
AD⊥BC(三线合一)
∵AB=AC,∠BAD=∠CAD (已知)
∴ BD=CD ,AD⊥BC(三线合一)
∵AB=AC, AD⊥BC (已知)
∴ BD=CD ,∠BAD=∠CAD (三线合一)
如图,位于在海上A、B两处的两艘救生船接到O处遇险船只的报警,当时测得∠A=∠B.如果这两艘救生船以同样的速度同时出发,能不能大约同时赶到出事地点(不考虑风浪因素)?
探究
在一个三角形中,如果有两个角相等,那么它们所对的边有什么关系?
已知:在△ABC中,∠B=∠C(如图).
求证:AB=AC.
2
1
D
C
A
B
证明
C
A
B
等腰三角形的判定定理:
如果一个三角形有两个角相等,那么这两个角所对的边也相等(简写成“等角对等边”).
结论
∵ ∠B=∠C (已知)
∴ AB=AC (等角对等边)
[例2]求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形.
已知: 如图, ∠CAE是△ABC的外角,∠1=∠2,AD∥BC.
求证:AB=AC.
应用
证明:∵AD∥BC,
∴∠1=∠B(两直线平行,同位角相等),
∠2=∠C(两直线平行,内错角相等).
又∵∠1=∠2,
∴∠B=∠C,
∴AB=AC(等角对等边).
角等
边等
判定
归纳
已知:如图,AD∥BC,BD平分∠ABC.
求证:AB=AD.
应用
例3 已知等腰三角形底边长为a,底边上的高的长为h,求作这个等腰三角形。
作法:1,作线段AB=a
2,作线段AB的垂直平分线MN,
与AB相交于点D。
3,在MN上取一点C,使DC=h.
4,连接AC,BC,则△ABC即为所求。
a
h
c
A
B
D
N
M
思考:在△ABC中,已知 ,BO平分∠ABC,CO平分∠ACB.
(1)请问图中有多少个等腰三角形 说明理由.
(2)线段EF和线段EB,FC之间有没有关系 若有是什么关系
AB=AC
AB≠AC
B
0
C
A
E
F
过点O作直线EF//BC交AB于E,交AC于F.
这节课你学到了什么
同学们再见
