人教版八年级上册 11.1.2三角形的高、中线和角平分线课件(共23张PPT)
文档属性
| 名称 | 人教版八年级上册 11.1.2三角形的高、中线和角平分线课件(共23张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 950.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-15 20:01:21 | ||
图片预览





文档简介
(共23张PPT)
第十一章11.1.2
三角形的高、中线和角平分线
学习目标:
一:理解三角形的高、中线和角平分线的定义, 会画出这三种重要的线段。
二:了解三角形的高、中线和角平分线的性质,并能应用它来解决实际问题。
重点与难点
重点:理解三角形的高、中线和角平分线的定义以及画法。
难点:了解各种线在三角形中所分得的角和线段之间的倍分关系。
2.线段中点的定义:
3.角平分线的定义:
1.垂线的定义:
一条射线把一个角分成两个相等的角,
这条射线叫做这个角的平分线。
把一条线段分成两条相等的线段的点。
当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线。
相关知识回顾
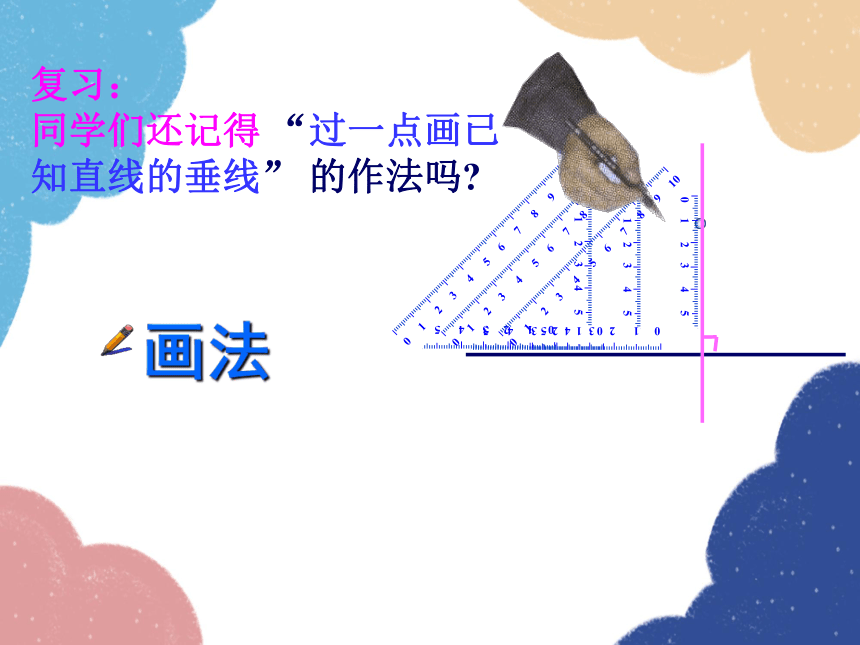
复习:
同学们还记得 “过一点画已知直线的垂线” 的作法吗
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
画法
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
三角形的高
A
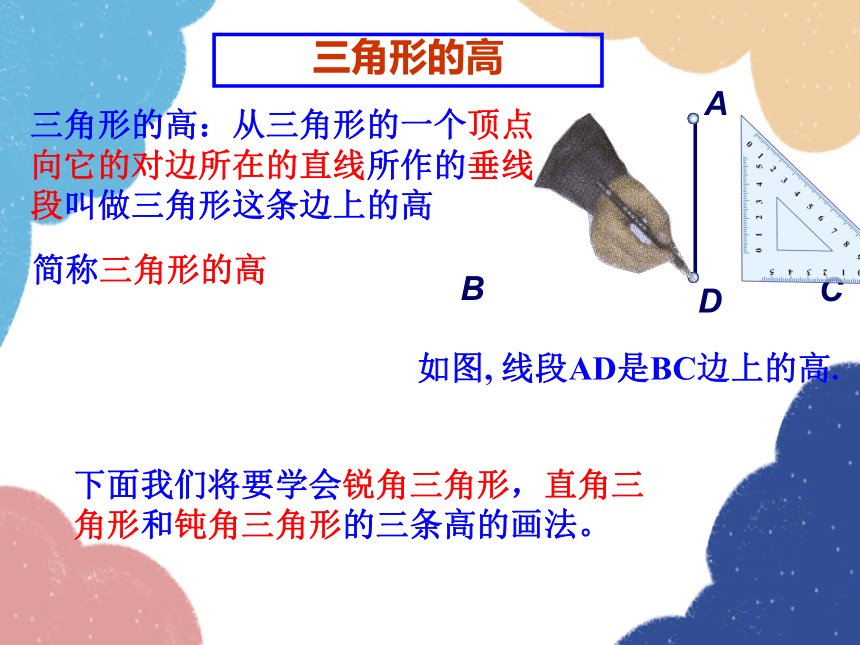
三角形的高:从三角形的一个顶点
向它的对边所在的直线所作的垂线段叫做三角形这条边上的高
B
C
D
简称三角形的高
如图, 线段AD是BC边上的高.
下面我们将要学会锐角三角形,直角三角形和钝角三角形的三条高的画法。
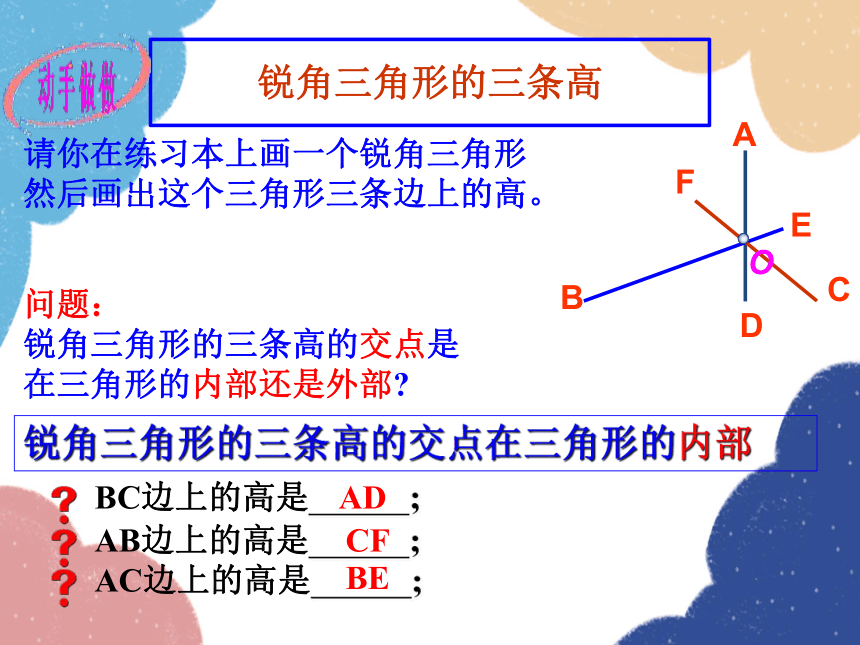
锐角三角形的三条高
请你在练习本上画一个锐角三角形
然后画出这个三角形三条边上的高。
O
问题:
锐角三角形的三条高的交点是在三角形的内部还是外部
锐角三角形的三条高的交点在三角形的内部
A
B
C
D
E
F
BC边上的高是 ;
AB边上的高是 ;
AC边上的高是 ;
AD
CF
BE
直角三角形的三条高
请你在练习本上画出一个直角三角形,然后画出它三条边上高。
A
B
C
直角边BC边上的高是 ;
AB
直角边AB边上的高是 ;
CB
D
斜边AC边上的高是 ;
BD
●
直角三角形的三条高的交点在三角形的顶点上
问题:
直角三角形三条边上的高的交点是在
三角形的内部、外部还是在顶点上呢?
钝角三角形的三条高
A
B
C
D
E
F
议一议
(1) 钝角三角形的
三条高交于一点吗?
钝 角三角形的
三条高不相交于一点
(2)三条高所在的直线交于一点吗?
钝角三角形的三条高所在直线交于一点
O
BC边上的高是____
AB边上的高是____
AC边上的高是____
画出钝角三形三条边上高
AD
CE
BF
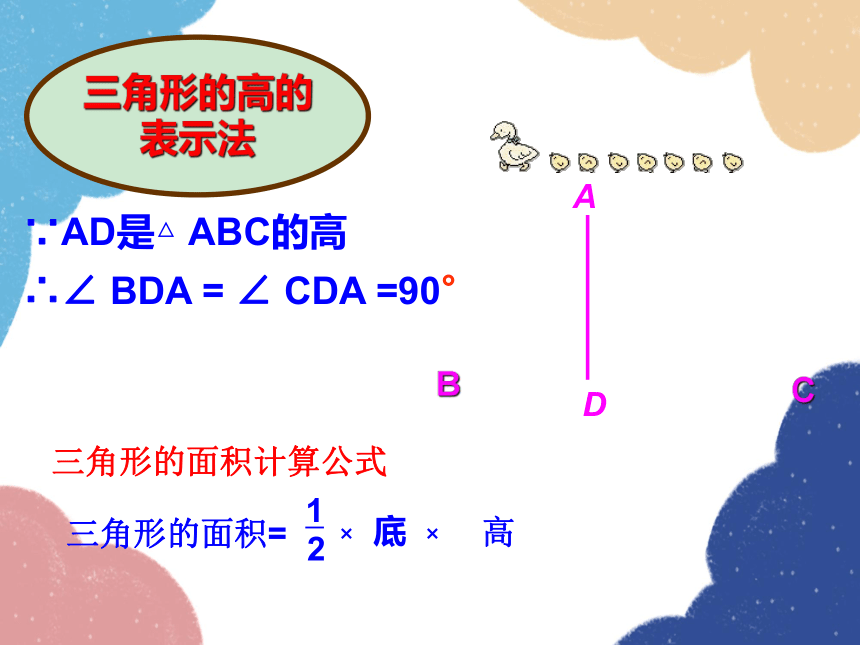
∵AD是△ ABC的高
A
B
C
D
∴∠ BDA = ∠ CDA =90°
三角形的高的
表示法
三角形的面积=
1
2
底
×
×
高
三角形的面积计算公式
拓展练习
2、 如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.锐角三角形
1、下列各组图形中,哪一组图形中AD是△ABC 的高( )
A
D
C
B
A
B
C
D
A
B
C
D
A
B
C
D
(A)
(B)
(C)
(D)
B
D
三角形的中线
在三角形中,从一个顶点向它所对的边的中点所连的线段叫做这条边的中线
A
B
C
D
∵AD是△ ABC的中线
∴BD=CD=
1
2
BC
●
●
三角形中线的理解
E
F
O
点D是BC中点
请你画出△ ABC的另外两条
边的中线
三角形的角平分线
叫做三角形的角平分线。
A
B
C
D
∵AD是 △ ABC的角平分线
∴∠ 1 = ∠ 2 =
1
2
∠BAC
任意画一个三角形,然后利用量角器画出
这个三角形三个角的角平分线,你发现了什么
●
●
在三角形中,一个
内角的角平分线与它的对边相交,
这个角的顶点与交点之间的线段,
三角形的三条角平分线相交于一点,交点在三角形的内部
︶
︶
1
2
A
C
B
F
E
D
O
∵BE是△ABC的角平分线
∴____=_____= _____
∴∠ACB=2______=2______
∠ABE
∠CBE
∠ABC
∠ACF
∵CF是△ABC的角平分线
∠BCF
角平分线的理解:
三角形的角平分线与角的平分线有什么区别?
思考
三角形的角平分线是一条线段 , 角的平分线是一条射线
拓展练习
3、填空:
(1)如图(1),AD,BE,CF是ΔABC的三条中线,则AB=2 ,BD=____,AE= 。
(2)如图(2), AD,BE,CF是ΔABC的三条角平分线,则∠1= , ∠3= _______ ∠ACB=2 。
AF
CD
AC
∠2
∠ABC
∠4
4.如图,在ΔABC中,AE是中线,AD是角平分线,AF是高。填空:
(1)BE= = ;
(2)∠BAD= = ;
(3)∠AFB= =90°;
拓展练习
CE
BC
∠CAD
∠BAC
∠AFC
拓展练习
5.如图1所示,在△ABC中,∠ACB=90°,把△ABC沿直线AC翻折180°,使点B 落在点B′的位置,则线段AC具有性质( )
A.是边BB′上的中线 B.是边BB′上的高
C.是∠BAB′的角平分线 D.以上三种性质合一
D
拓展练习
6.如图所示,D,E分别是△ABC的边AC,BC的中点,则
下列说法不正确的是( )
A.DE是△BCD的中线 B.BD是△ABC的中线
C.AD=DC,BE=EC D.CE=CD
D
今天我们学了什么呀?
1.三角形的高、中线、角平分线等有关概念
及它们的画法。
2. .三角形的高、中线、角平分线
几何表达及简单应用。
知识小结
三角形的
重要线段 概念 图形 表示法
三角形
的高线 从三角形的一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段 ∵AD是△ABC的BC上的高线.
∴AD⊥BC
∠ADB=∠ADC=90°.
三角形
的中线 三角形中,连结一个顶点和它对边中的
线段 ∵ AD是△ABC的BC上的中线.
∴ BD=CD= BC.
三角形的
角平分线 三角形一个内角的平分线与它的对边相交,这个角顶点与交点之间的线段 ∵.AD是△ABC的∠BAC的平分线
∴ ∠1=∠2= ∠BAC
知识归纳
作业:
习题11.1第4题
再见
第十一章11.1.2
三角形的高、中线和角平分线
学习目标:
一:理解三角形的高、中线和角平分线的定义, 会画出这三种重要的线段。
二:了解三角形的高、中线和角平分线的性质,并能应用它来解决实际问题。
重点与难点
重点:理解三角形的高、中线和角平分线的定义以及画法。
难点:了解各种线在三角形中所分得的角和线段之间的倍分关系。
2.线段中点的定义:
3.角平分线的定义:
1.垂线的定义:
一条射线把一个角分成两个相等的角,
这条射线叫做这个角的平分线。
把一条线段分成两条相等的线段的点。
当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线。
相关知识回顾
复习:
同学们还记得 “过一点画已知直线的垂线” 的作法吗
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
画法
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
三角形的高
A
三角形的高:从三角形的一个顶点
向它的对边所在的直线所作的垂线段叫做三角形这条边上的高
B
C
D
简称三角形的高
如图, 线段AD是BC边上的高.
下面我们将要学会锐角三角形,直角三角形和钝角三角形的三条高的画法。
锐角三角形的三条高
请你在练习本上画一个锐角三角形
然后画出这个三角形三条边上的高。
O
问题:
锐角三角形的三条高的交点是在三角形的内部还是外部
锐角三角形的三条高的交点在三角形的内部
A
B
C
D
E
F
BC边上的高是 ;
AB边上的高是 ;
AC边上的高是 ;
AD
CF
BE
直角三角形的三条高
请你在练习本上画出一个直角三角形,然后画出它三条边上高。
A
B
C
直角边BC边上的高是 ;
AB
直角边AB边上的高是 ;
CB
D
斜边AC边上的高是 ;
BD
●
直角三角形的三条高的交点在三角形的顶点上
问题:
直角三角形三条边上的高的交点是在
三角形的内部、外部还是在顶点上呢?
钝角三角形的三条高
A
B
C
D
E
F
议一议
(1) 钝角三角形的
三条高交于一点吗?
钝 角三角形的
三条高不相交于一点
(2)三条高所在的直线交于一点吗?
钝角三角形的三条高所在直线交于一点
O
BC边上的高是____
AB边上的高是____
AC边上的高是____
画出钝角三形三条边上高
AD
CE
BF
∵AD是△ ABC的高
A
B
C
D
∴∠ BDA = ∠ CDA =90°
三角形的高的
表示法
三角形的面积=
1
2
底
×
×
高
三角形的面积计算公式
拓展练习
2、 如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.锐角三角形
1、下列各组图形中,哪一组图形中AD是△ABC 的高( )
A
D
C
B
A
B
C
D
A
B
C
D
A
B
C
D
(A)
(B)
(C)
(D)
B
D
三角形的中线
在三角形中,从一个顶点向它所对的边的中点所连的线段叫做这条边的中线
A
B
C
D
∵AD是△ ABC的中线
∴BD=CD=
1
2
BC
●
●
三角形中线的理解
E
F
O
点D是BC中点
请你画出△ ABC的另外两条
边的中线
三角形的角平分线
叫做三角形的角平分线。
A
B
C
D
∵AD是 △ ABC的角平分线
∴∠ 1 = ∠ 2 =
1
2
∠BAC
任意画一个三角形,然后利用量角器画出
这个三角形三个角的角平分线,你发现了什么
●
●
在三角形中,一个
内角的角平分线与它的对边相交,
这个角的顶点与交点之间的线段,
三角形的三条角平分线相交于一点,交点在三角形的内部
︶
︶
1
2
A
C
B
F
E
D
O
∵BE是△ABC的角平分线
∴____=_____= _____
∴∠ACB=2______=2______
∠ABE
∠CBE
∠ABC
∠ACF
∵CF是△ABC的角平分线
∠BCF
角平分线的理解:
三角形的角平分线与角的平分线有什么区别?
思考
三角形的角平分线是一条线段 , 角的平分线是一条射线
拓展练习
3、填空:
(1)如图(1),AD,BE,CF是ΔABC的三条中线,则AB=2 ,BD=____,AE= 。
(2)如图(2), AD,BE,CF是ΔABC的三条角平分线,则∠1= , ∠3= _______ ∠ACB=2 。
AF
CD
AC
∠2
∠ABC
∠4
4.如图,在ΔABC中,AE是中线,AD是角平分线,AF是高。填空:
(1)BE= = ;
(2)∠BAD= = ;
(3)∠AFB= =90°;
拓展练习
CE
BC
∠CAD
∠BAC
∠AFC
拓展练习
5.如图1所示,在△ABC中,∠ACB=90°,把△ABC沿直线AC翻折180°,使点B 落在点B′的位置,则线段AC具有性质( )
A.是边BB′上的中线 B.是边BB′上的高
C.是∠BAB′的角平分线 D.以上三种性质合一
D
拓展练习
6.如图所示,D,E分别是△ABC的边AC,BC的中点,则
下列说法不正确的是( )
A.DE是△BCD的中线 B.BD是△ABC的中线
C.AD=DC,BE=EC D.CE=CD
D
今天我们学了什么呀?
1.三角形的高、中线、角平分线等有关概念
及它们的画法。
2. .三角形的高、中线、角平分线
几何表达及简单应用。
知识小结
三角形的
重要线段 概念 图形 表示法
三角形
的高线 从三角形的一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段 ∵AD是△ABC的BC上的高线.
∴AD⊥BC
∠ADB=∠ADC=90°.
三角形
的中线 三角形中,连结一个顶点和它对边中的
线段 ∵ AD是△ABC的BC上的中线.
∴ BD=CD= BC.
三角形的
角平分线 三角形一个内角的平分线与它的对边相交,这个角顶点与交点之间的线段 ∵.AD是△ABC的∠BAC的平分线
∴ ∠1=∠2= ∠BAC
知识归纳
作业:
习题11.1第4题
再见
