苏教版 五年级上册数学 面积那点事 课件(共21张PPT)
文档属性
| 名称 | 苏教版 五年级上册数学 面积那点事 课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-15 19:53:43 | ||
图片预览







文档简介
(共21张PPT)
面 积 那 点 事
义务教育阶段 苏教版五年级数学上册
课前准备
1.请准备好作业本、文具用品。
2.听课过程中可通过按暂停键进行思考和答题,完成后再继续观看。
公顷、平方千米
组合图形的面积
不规则图形的面积
回顾:本周主要学习了哪些知识呢?
内容回顾
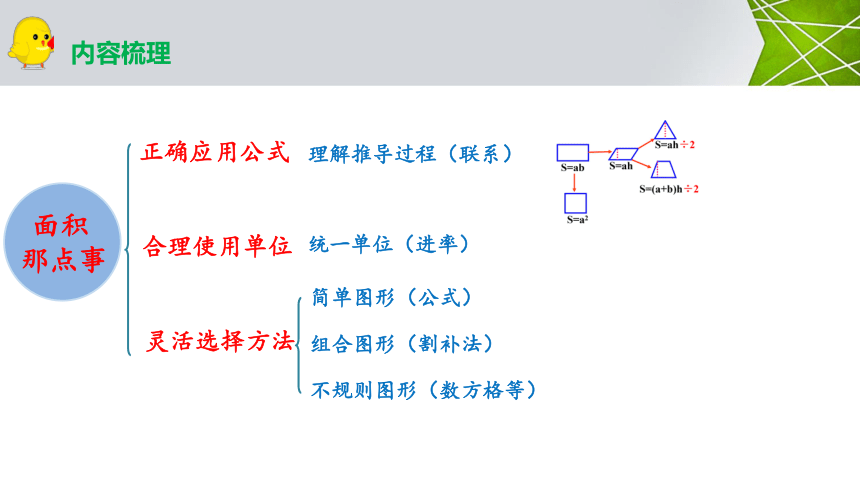
正确应用公式
内容梳理
合理使用单位
灵活选择方法
简单图形(公式)
组合图形(割补法)
不规则图形(数方格等)
统一单位(进率)
理解推导过程(联系)
面积
那点事
典型例题
1.填写合适的数。
3公顷=( )平方米 3600公顷=( )平方千米
2平方千米=( )公顷 500000平方米=( )公顷
7平方千米=( )平方米 8000000平方米=( )平方千米
高级单位
乘进率
除以进率
低级单位
典型例题
公 顷
平方厘米
平方分米
平方千米
平方米
100
100
100
10000
公 顷
平方厘米
平方分米
平方千米
平方米
100
100
100
10000
公 亩
100
100
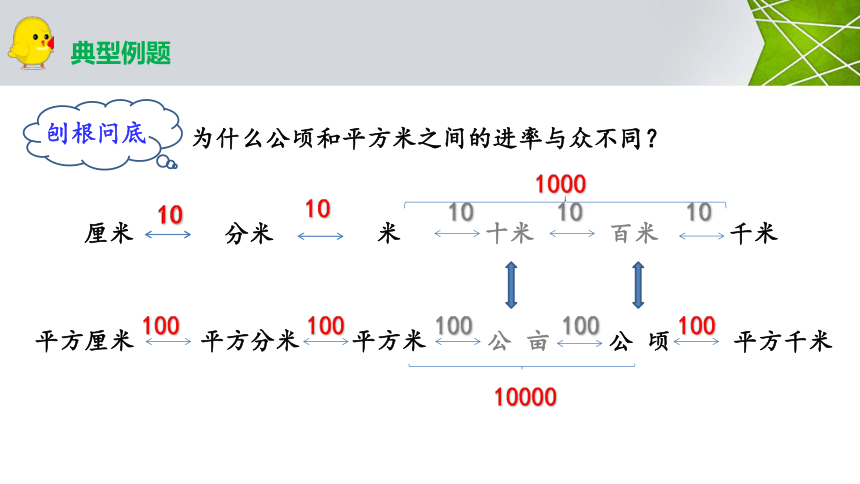
厘米
分米
米
10
10
十米
百米
千米
10
10
10
1000
典型例题
刨根问底
为什么公顷和平方米之间的进率与众不同?
10
典型例题
1.填写合适的数。
3公顷=( )平方米 3600公顷=( )平方千米
2平方千米=( )公顷 500000平方米=( )公顷
7平方千米=( )平方米 8000000平方米=( )平方千米
30000
36
200
50
×10000
÷100
×100
÷10000
7000000
8
÷1000000
×1000000
高级单位
乘进率
除以进率
低级单位
2.计算下面图形的面积。(单位:厘米)
典型例题
5×6=30(平方厘米)
30+15=45(平方厘米)
长方形面积:
梯形的面积:
总面积:
(5+10)×(8-6)÷2
=15×2÷2
=15(平方厘米)
分割
2.计算下面图形的面积。(单位:厘米)
典型例题
2.计算下面图形的面积。(单位:厘米)
典型例题
10×8=80(平方厘米)
80-35=45(平方厘米)
长方形面积:
梯形面积:
总面积:
(6+8)×(10-5)÷2
=14×5÷2
=35(平方厘米)
添补
典型例题
分割
分割
分割
添补
分割成几个简单图形,分别算出面积,再求和。
添补成简单的图形,从补成的图形中去掉一部分。
组合图形
转化
(割补法)
基本图形
典型例题
根据图形特点,选择合理、简便的方法
在利用割补法进行转化的过程中要注意什么?
组合图形
转化
(割补法)
基本图形
刨根问底
典型例题
3.不规则图形面积计算。
估算
只算整格,得到的结果比实际面积小。
不满整格当作整格,得到的结果比实际面积大。
(实际面积的范围在这两种结果之间。)
先数整格的,再数不满整格的,把不满整格的
按半格计算,让估算的结果更加接近实际面积。
典型例题
转化
转化
刨根问底
不规则图形面积的计算,只能用数方格的方法吗?
1.如果每间教室以50平方米计算,那么1公顷的地方相当于( )间这样的教室。
A. 20 B. 200 C. 2000 D. 50
巩固练习
10000÷50=200(间)
B
1公顷=10000平方米
巩固练习
2.下图是由两个正方形组成,求阴影部分的面积。(单位:米)
8
4
总:8×8+4×4=80(平方米)
三角形:(8+4)×8÷2=48(平方米)
阴影:80-48=32 (平方米)
整体思考
拓展练习
3.如图,在直角三角形内剪下了一个正方形,正方形的四个顶点均在直角三角形的边上,其中斜边上的顶点将斜边分成8厘米和5厘米两端。求两个阴影三角形的面积一共有多少平方厘米?
8
5
8×5÷2=20(平方厘米)
动态转化
探索新知
4.在下图中,平行四边形ABCD的边BC长10厘米,直角三角形ECB的直角边EC长8厘米,已知阴影部分的总面积比三角形EFG的面积大10平方厘米,求CG的长度。
阴影部分+中间白色梯形EFBC
利用“桥梁”
三角形EFG+中间白色梯形EFBC
平行四边形ABCD
大三角形BCG
平行四边形ABCD:10×8=80(平方厘米)
大三角形BCG:80-10=70(平方厘米)
CG:70×2÷10=14(厘米)
10
总结梳理
正确应用公式
合理使用单位
灵活选择方法
简单图形(公式)
组合图形(割补法)
不规则图形(数方格等)
统一单位(进率)
理解推导过程(关系)
面积
那点事
转化
整体、联系
合理、简便
通过今天的学习,你有哪些收获?
下课了!
再见!
面 积 那 点 事
义务教育阶段 苏教版五年级数学上册
课前准备
1.请准备好作业本、文具用品。
2.听课过程中可通过按暂停键进行思考和答题,完成后再继续观看。
公顷、平方千米
组合图形的面积
不规则图形的面积
回顾:本周主要学习了哪些知识呢?
内容回顾
正确应用公式
内容梳理
合理使用单位
灵活选择方法
简单图形(公式)
组合图形(割补法)
不规则图形(数方格等)
统一单位(进率)
理解推导过程(联系)
面积
那点事
典型例题
1.填写合适的数。
3公顷=( )平方米 3600公顷=( )平方千米
2平方千米=( )公顷 500000平方米=( )公顷
7平方千米=( )平方米 8000000平方米=( )平方千米
高级单位
乘进率
除以进率
低级单位
典型例题
公 顷
平方厘米
平方分米
平方千米
平方米
100
100
100
10000
公 顷
平方厘米
平方分米
平方千米
平方米
100
100
100
10000
公 亩
100
100
厘米
分米
米
10
10
十米
百米
千米
10
10
10
1000
典型例题
刨根问底
为什么公顷和平方米之间的进率与众不同?
10
典型例题
1.填写合适的数。
3公顷=( )平方米 3600公顷=( )平方千米
2平方千米=( )公顷 500000平方米=( )公顷
7平方千米=( )平方米 8000000平方米=( )平方千米
30000
36
200
50
×10000
÷100
×100
÷10000
7000000
8
÷1000000
×1000000
高级单位
乘进率
除以进率
低级单位
2.计算下面图形的面积。(单位:厘米)
典型例题
5×6=30(平方厘米)
30+15=45(平方厘米)
长方形面积:
梯形的面积:
总面积:
(5+10)×(8-6)÷2
=15×2÷2
=15(平方厘米)
分割
2.计算下面图形的面积。(单位:厘米)
典型例题
2.计算下面图形的面积。(单位:厘米)
典型例题
10×8=80(平方厘米)
80-35=45(平方厘米)
长方形面积:
梯形面积:
总面积:
(6+8)×(10-5)÷2
=14×5÷2
=35(平方厘米)
添补
典型例题
分割
分割
分割
添补
分割成几个简单图形,分别算出面积,再求和。
添补成简单的图形,从补成的图形中去掉一部分。
组合图形
转化
(割补法)
基本图形
典型例题
根据图形特点,选择合理、简便的方法
在利用割补法进行转化的过程中要注意什么?
组合图形
转化
(割补法)
基本图形
刨根问底
典型例题
3.不规则图形面积计算。
估算
只算整格,得到的结果比实际面积小。
不满整格当作整格,得到的结果比实际面积大。
(实际面积的范围在这两种结果之间。)
先数整格的,再数不满整格的,把不满整格的
按半格计算,让估算的结果更加接近实际面积。
典型例题
转化
转化
刨根问底
不规则图形面积的计算,只能用数方格的方法吗?
1.如果每间教室以50平方米计算,那么1公顷的地方相当于( )间这样的教室。
A. 20 B. 200 C. 2000 D. 50
巩固练习
10000÷50=200(间)
B
1公顷=10000平方米
巩固练习
2.下图是由两个正方形组成,求阴影部分的面积。(单位:米)
8
4
总:8×8+4×4=80(平方米)
三角形:(8+4)×8÷2=48(平方米)
阴影:80-48=32 (平方米)
整体思考
拓展练习
3.如图,在直角三角形内剪下了一个正方形,正方形的四个顶点均在直角三角形的边上,其中斜边上的顶点将斜边分成8厘米和5厘米两端。求两个阴影三角形的面积一共有多少平方厘米?
8
5
8×5÷2=20(平方厘米)
动态转化
探索新知
4.在下图中,平行四边形ABCD的边BC长10厘米,直角三角形ECB的直角边EC长8厘米,已知阴影部分的总面积比三角形EFG的面积大10平方厘米,求CG的长度。
阴影部分+中间白色梯形EFBC
利用“桥梁”
三角形EFG+中间白色梯形EFBC
平行四边形ABCD
大三角形BCG
平行四边形ABCD:10×8=80(平方厘米)
大三角形BCG:80-10=70(平方厘米)
CG:70×2÷10=14(厘米)
10
总结梳理
正确应用公式
合理使用单位
灵活选择方法
简单图形(公式)
组合图形(割补法)
不规则图形(数方格等)
统一单位(进率)
理解推导过程(关系)
面积
那点事
转化
整体、联系
合理、简便
通过今天的学习,你有哪些收获?
下课了!
再见!
