苏教版 五年级上册数学 巧用“弦图”解决面积问题 课件(共15张PPT)
文档属性
| 名称 | 苏教版 五年级上册数学 巧用“弦图”解决面积问题 课件(共15张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 5.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-15 19:55:13 | ||
图片预览



文档简介
(共15张PPT)
巧用“弦图”
解决面积问题
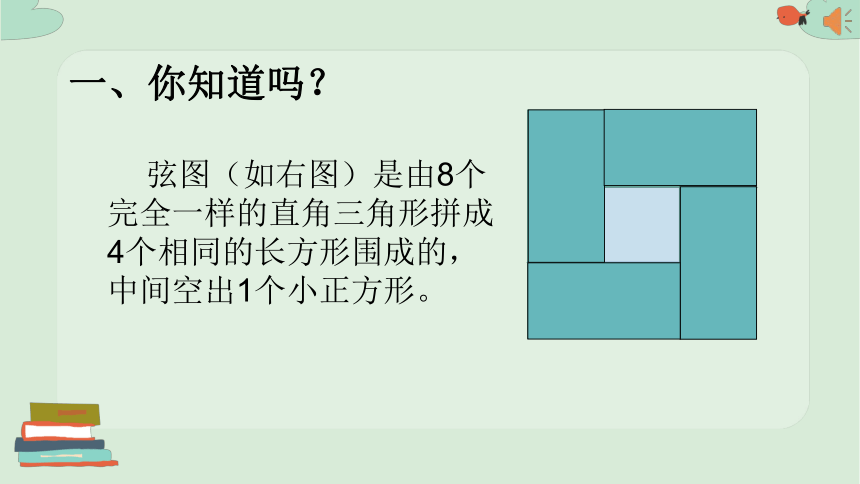
一、你知道吗?
弦图(如右图)是由8个完全一样的直角三角形拼成4个相同的长方形围成的,中间空出1个小正方形。
三国时期,中国数学家在对《周髀算经》作注释时,就利用“弦图”对勾股定理作出了严格而简明的证明。
一、你知道吗?
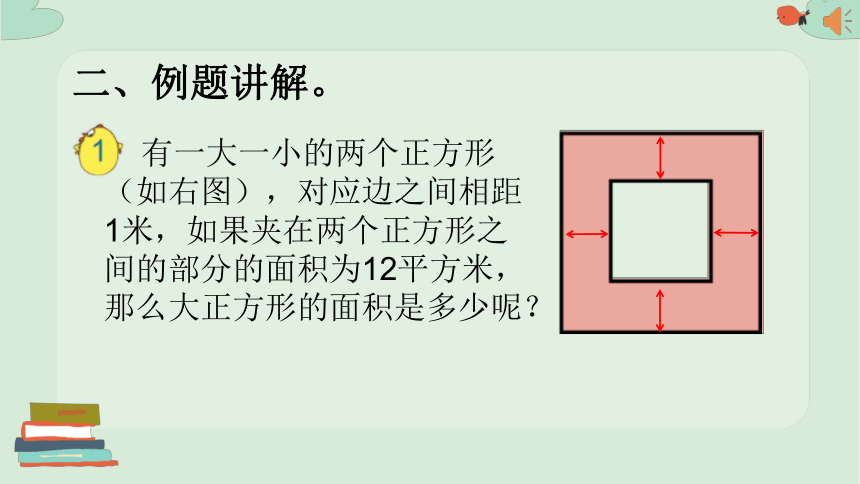
二、例题讲解。
有一大一小的两个正方形(如右图),对应边之间相距1米,如果夹在两个正方形之间的部分的面积为12平方米,那么大正方形的面积是多少呢?
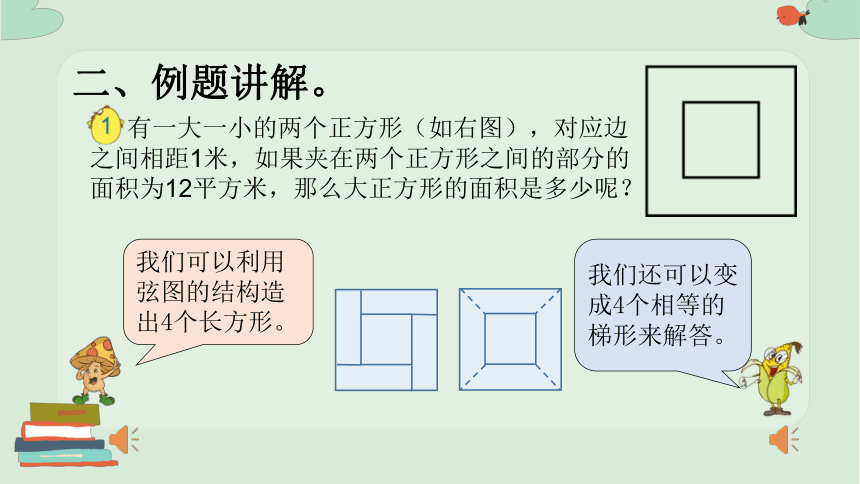
二、例题讲解。
有一大一小的两个正方形(如右图),对应边之间相距1米,如果夹在两个正方形之间的部分的面积为12平方米,那么大正方形的面积是多少呢?
我们可以利用弦图的结构造出4个长方形。
我们还可以变成4个相等的梯形来解答。
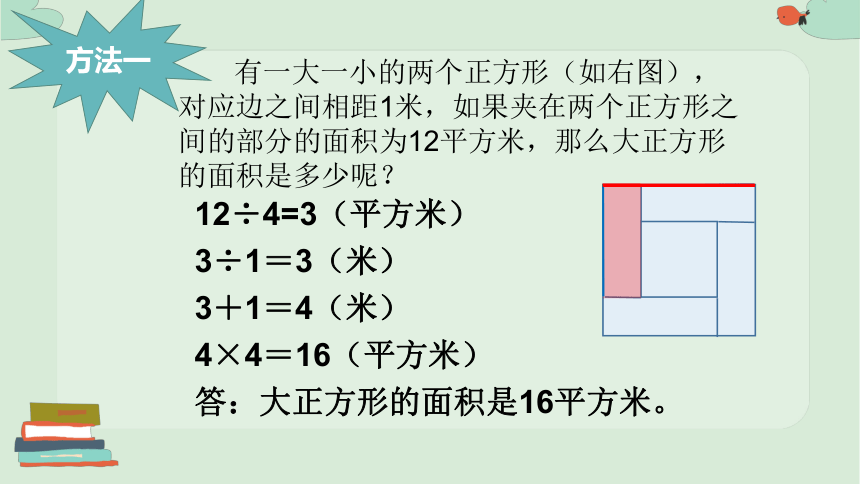
有一大一小的两个正方形(如右图),对应边之间相距1米,如果夹在两个正方形之间的部分的面积为12平方米,那么大正方形的面积是多少呢?
12÷4=3(平方米)
方法一
3÷1=3(米)
3+1=4(米)
4×4=16(平方米)
答:大正方形的面积是16平方米。
有一大一小的两个正方形(如右图),对应边之间相距1米,如果夹在两个正方形之间的部分的面积为12平方米,那么大正方形的面积是多少呢?
12÷4=3(平方米)
3×2÷1=6(米)
(6+2)÷2=4(米)
4×4=16(平方米)
答:大正方形的面积是16平方米。
方法二
上下底之和是6米,上下底之差是2米。
二、例题讲解。
有一大一小的两个正方形(如右图),对应边之间相距1米,如果夹在两个正方形之间的部分的面积为12平方米,那么大正方形的面积是多少呢?
12-1×4=8(平方米)
8÷4=2(平方米)
2÷1=2(米)
4×4=16(平方米)
答:大正方形的面积是16平方米。
2+1+1=4(米)
有一大一小的两个正方形(如右图),对应边之间相距1米,如果夹在两个正方形之间的部分的面积为12平方米,那么大正方形的面积是多少呢?
方法三
12÷2=6(平方米)
6×2÷2=6(米)
(6+2)÷2=4(米)
4×4=16(平方米)
答:大正方形的面积是16平方米。
有一大一小的两个正方形(如右图),对应边之间相距1米,如果夹在两个正方形之间的部分的面积为12平方米,那么大正方形的面积是多少呢?
方法四
上下底之和是6米,上下底之差是2米。
2米
观察例1,解决这个问题关键要做什么
在求面积过程中我们可以根据“弦图”巧添辅助线,关键是将图形转化成已学过的图形,从而解决问题。
三、美丽的“弦图”
四、练习巩固。
6米
有一大一小的两个正方形试验田(如右图),它们的周长相差40米,面积相差220平方米,那么小正方形试验田的面积是多少平方米?
A
B
C
D
D:40÷4=10(米)
B、C:220-100=120(平方米)
10米
A:60÷10=6(米)
答:小正方形试验田的面积是36平方米。
10×10=100(平方米)
120÷2=60(平方米)
6×6=36(平方米)
如图,用四个相同的长方形拼成一个面积为100平方厘米的大正方形,每个长方形的周长是多少厘米?
因为100=10×10
所以大正方形的边长=10厘米
长方形的长+宽=大正方形的边长=10厘米
每个长方形的周长=10×2=20厘米
答:每个长方形的周长是20厘米。
10厘米
四、练习巩固。
谢谢大家
巧用“弦图”
解决面积问题
一、你知道吗?
弦图(如右图)是由8个完全一样的直角三角形拼成4个相同的长方形围成的,中间空出1个小正方形。
三国时期,中国数学家在对《周髀算经》作注释时,就利用“弦图”对勾股定理作出了严格而简明的证明。
一、你知道吗?
二、例题讲解。
有一大一小的两个正方形(如右图),对应边之间相距1米,如果夹在两个正方形之间的部分的面积为12平方米,那么大正方形的面积是多少呢?
二、例题讲解。
有一大一小的两个正方形(如右图),对应边之间相距1米,如果夹在两个正方形之间的部分的面积为12平方米,那么大正方形的面积是多少呢?
我们可以利用弦图的结构造出4个长方形。
我们还可以变成4个相等的梯形来解答。
有一大一小的两个正方形(如右图),对应边之间相距1米,如果夹在两个正方形之间的部分的面积为12平方米,那么大正方形的面积是多少呢?
12÷4=3(平方米)
方法一
3÷1=3(米)
3+1=4(米)
4×4=16(平方米)
答:大正方形的面积是16平方米。
有一大一小的两个正方形(如右图),对应边之间相距1米,如果夹在两个正方形之间的部分的面积为12平方米,那么大正方形的面积是多少呢?
12÷4=3(平方米)
3×2÷1=6(米)
(6+2)÷2=4(米)
4×4=16(平方米)
答:大正方形的面积是16平方米。
方法二
上下底之和是6米,上下底之差是2米。
二、例题讲解。
有一大一小的两个正方形(如右图),对应边之间相距1米,如果夹在两个正方形之间的部分的面积为12平方米,那么大正方形的面积是多少呢?
12-1×4=8(平方米)
8÷4=2(平方米)
2÷1=2(米)
4×4=16(平方米)
答:大正方形的面积是16平方米。
2+1+1=4(米)
有一大一小的两个正方形(如右图),对应边之间相距1米,如果夹在两个正方形之间的部分的面积为12平方米,那么大正方形的面积是多少呢?
方法三
12÷2=6(平方米)
6×2÷2=6(米)
(6+2)÷2=4(米)
4×4=16(平方米)
答:大正方形的面积是16平方米。
有一大一小的两个正方形(如右图),对应边之间相距1米,如果夹在两个正方形之间的部分的面积为12平方米,那么大正方形的面积是多少呢?
方法四
上下底之和是6米,上下底之差是2米。
2米
观察例1,解决这个问题关键要做什么
在求面积过程中我们可以根据“弦图”巧添辅助线,关键是将图形转化成已学过的图形,从而解决问题。
三、美丽的“弦图”
四、练习巩固。
6米
有一大一小的两个正方形试验田(如右图),它们的周长相差40米,面积相差220平方米,那么小正方形试验田的面积是多少平方米?
A
B
C
D
D:40÷4=10(米)
B、C:220-100=120(平方米)
10米
A:60÷10=6(米)
答:小正方形试验田的面积是36平方米。
10×10=100(平方米)
120÷2=60(平方米)
6×6=36(平方米)
如图,用四个相同的长方形拼成一个面积为100平方厘米的大正方形,每个长方形的周长是多少厘米?
因为100=10×10
所以大正方形的边长=10厘米
长方形的长+宽=大正方形的边长=10厘米
每个长方形的周长=10×2=20厘米
答:每个长方形的周长是20厘米。
10厘米
四、练习巩固。
谢谢大家
