江苏省安宜高级中学2013-2014学年高一上学期期中考试数学试题
文档属性
| 名称 | 江苏省安宜高级中学2013-2014学年高一上学期期中考试数学试题 |

|
|
| 格式 | zip | ||
| 文件大小 | 177.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-11-09 00:00:00 | ||
图片预览



文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
江苏省安宜高级中学2013-2014学年高一上学期期中考试数学试题
一、填空题(本大题共14小题,每小题5分,计70分)
1、设集合,,则 ▲ .
2、用列举法表示集合,其结果应为A= ▲ .
3、设,,则= ▲ .
4、下列各组函数中,是同一个函数的有 ▲ .(填写序号)
①与 ②与
③与 ④与
5、函数的定义域是 ▲ .
6、式子用分数指数幂表示为 ▲ .
7、计算:= ▲ .
8、函数在区间上的最大值是,则 ▲ .
9、已知,则这三个数的大小关系是 ▲ .
(按从小到大的顺序)
10、已知函数,若,则 ▲ .
11、下列对应关系中,是从A到B的映射的有 ▲ .(填写序号)
①,,
②,, A中的元素对应它除以3所得的余数;
③,
12、函数的单调减区间是 ▲ .
13、已知函数满足 且当时总有,其中. 若,则实数的取值范围是 ▲ .
14、已知函数是定义域为的奇函数,在区间上单调递增,且. 若,则的取值范围是 ▲ .
二、解答题 (共6道题,计90分)
15.(本题满分14分)
设全集为, 集合或,.
(1)求,;
(2)已知,若,求实数的取值范围.
16、(本题满分14分)
(1)解方程:
(2)解不等式:
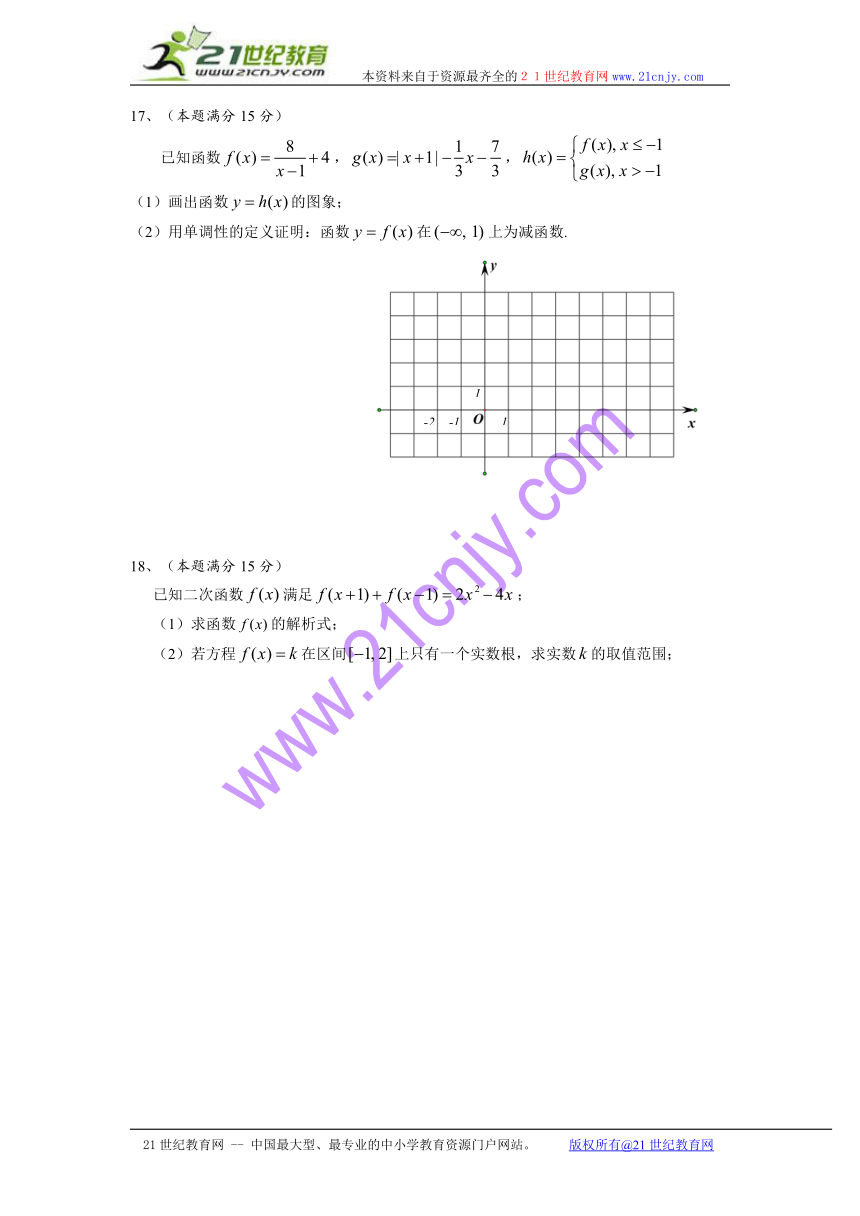
17、(本题满分15分)
已知函数,,
(1)画出函数的图象;
(2)用单调性的定义证明:函数在上为减函数.
18、(本题满分15分)
已知二次函数满足;
(1)求函数的解析式;
(2)若方程在区间上只有一个实数根,求实数的取值范围;
19、(本题满分16分)
提高过江大桥的车辆通行能力可改善整个城市的交通状况.在一般情况下,大桥上的车流速度(单位:千米/小时)是车流密度(单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时.研究表明:当时,车流速度是车流密度的一次函数,即(为常数).
(1)当时,求函数的表达式;
(2)当车流密度为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时) 可以达到最大,并求出最大值.(精确到1辆/小时)
20、(本题满分16分)
已知函数为偶函数.
(1)求实数的值;
(2)当时,恒成立,求m的取值范围.
高一数学期中考试答案20131105
一、填空题(本大题共14小题,每小题5分,计70分)
1、 2、 3、 4、③④ 5、
6、 7、 8、 9、 10、 11、①②
12、 13、 14、
二、解答题:
15、(本题满分14分)
解:(1)=R………………………3分(画数轴略,不画数轴不扣分)
, ∴…………9分
(2)∵,且, ∴…………12分
∴所求实数的取值范围是 …………14分
注:未考虑等号的,各扣1分,计扣2分。
16、(本题满分14分)
解:(1)原方程可化为: ………2分
由于, 所以只有 ………5分
所以原方程的根为 ………7分
(2)原不等式可化为:,
即: ………9分,
, ………12分
所以原不等式的解集为………14分
17、(本题满分15分)
解:(1)函数的图象
当时,
取点和,得射线;……3分
对,取点和
函数的图象如图所示。………7分
注:时的图象,未经过整点和的,扣1分;画到x轴下方的,扣1分,图象上凸画成上凹的,此段不得分,即扣4分。
射线部分,画成不经过整点和的,扣1分,点画成实点的,扣1分;
【建议】:教学中要强化对画图象的规范要求。教师示范,适当练习。
(2)任取,设,…………9分
因为
则 …………11分
而 又 …………13分
所以, 即: …………14分
所以函数在上为减函数. …………15分
18、(本题满分15分)
解:(1)设,所以,
,
…………2分
∴ …………4分
由条件得,
∴函数的解析式 …………7分
(2)函数 ,的图象如图所示 …………10分
当直线与图角的交点情况是:
当时,只有一个交点;
当时,有两个交点;
当时,只有一个交点;…………14分
所以,方程在区间上只有一个实数根,
此时或 …………15分
另解:
方程可化为:
当时,有两个实根: ………10分
时,
时,, 此时方程在区间上有两个根。
时,,此时方程在区间上只有一个根………14分
所以,若方程在区间上只有一个实数根,
的取值范围是。………15分
说明:用代数法讨论时,如果将两个相等的根,不认为是一个根,则不扣分。事实上,用代数法讨论时,注意到对称轴是,则大根在区间内,小根必在;小根不在区间,大根则必不在,这样讨论会很清晰。
19、(本题满分16分)
解:(1)由题意:当0≤x≤20时,v(x)=60;…………………2分
当20≤x≤200时,设v(x)=kx+b,
再由已知,得解得 …………………5分
故函数v(x)的表达式为…………………7分
(2)依题意并由(1)可得 …………………9分
当0≤x≤20时,f(x)为增函数,
故当x=20时,其最大值为60×20=1200; ………………… 11分
当20<x≤200时,f(x)=x(200-x) =
所以当且仅当x=100时,f(x) 最大值为
所以,当x=100时,f(x)在区间(20,200]上取得最大值 . ……14分
综上,当x=100时,f(x)在区间[0,200]上取得最大值≈3333,. ……15分
答:当车流密度为100 辆/千米时,车流量可以达到最大,最大值约为3333辆/小时.……………16分 .
20、(本题满分16分)
解:(1)因为,函数为偶函数.
由,得x(+a)=-x(+a),…………3分
2a=-(+)=1,…………5分
解得,a= 经检验 a=符合题意. …………7分
注:若由特殊值求出a=,一定要检验是否恒成立。否则扣3分.
(2)恒成立对恒成立,
∴
∴ …………8分
∵+在[1,3]上为减函数, …………10分
∴对恒成立 …………13分
∴ …………15分
所以m的取值范围是 …………16分
-2
-1
1
1
-2
-1
1
1
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
江苏省安宜高级中学2013-2014学年高一上学期期中考试数学试题
一、填空题(本大题共14小题,每小题5分,计70分)
1、设集合,,则 ▲ .
2、用列举法表示集合,其结果应为A= ▲ .
3、设,,则= ▲ .
4、下列各组函数中,是同一个函数的有 ▲ .(填写序号)
①与 ②与
③与 ④与
5、函数的定义域是 ▲ .
6、式子用分数指数幂表示为 ▲ .
7、计算:= ▲ .
8、函数在区间上的最大值是,则 ▲ .
9、已知,则这三个数的大小关系是 ▲ .
(按从小到大的顺序)
10、已知函数,若,则 ▲ .
11、下列对应关系中,是从A到B的映射的有 ▲ .(填写序号)
①,,
②,, A中的元素对应它除以3所得的余数;
③,
12、函数的单调减区间是 ▲ .
13、已知函数满足 且当时总有,其中. 若,则实数的取值范围是 ▲ .
14、已知函数是定义域为的奇函数,在区间上单调递增,且. 若,则的取值范围是 ▲ .
二、解答题 (共6道题,计90分)
15.(本题满分14分)
设全集为, 集合或,.
(1)求,;
(2)已知,若,求实数的取值范围.
16、(本题满分14分)
(1)解方程:
(2)解不等式:
17、(本题满分15分)
已知函数,,
(1)画出函数的图象;
(2)用单调性的定义证明:函数在上为减函数.
18、(本题满分15分)
已知二次函数满足;
(1)求函数的解析式;
(2)若方程在区间上只有一个实数根,求实数的取值范围;
19、(本题满分16分)
提高过江大桥的车辆通行能力可改善整个城市的交通状况.在一般情况下,大桥上的车流速度(单位:千米/小时)是车流密度(单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时.研究表明:当时,车流速度是车流密度的一次函数,即(为常数).
(1)当时,求函数的表达式;
(2)当车流密度为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时) 可以达到最大,并求出最大值.(精确到1辆/小时)
20、(本题满分16分)
已知函数为偶函数.
(1)求实数的值;
(2)当时,恒成立,求m的取值范围.
高一数学期中考试答案20131105
一、填空题(本大题共14小题,每小题5分,计70分)
1、 2、 3、 4、③④ 5、
6、 7、 8、 9、 10、 11、①②
12、 13、 14、
二、解答题:
15、(本题满分14分)
解:(1)=R………………………3分(画数轴略,不画数轴不扣分)
, ∴…………9分
(2)∵,且, ∴…………12分
∴所求实数的取值范围是 …………14分
注:未考虑等号的,各扣1分,计扣2分。
16、(本题满分14分)
解:(1)原方程可化为: ………2分
由于, 所以只有 ………5分
所以原方程的根为 ………7分
(2)原不等式可化为:,
即: ………9分,
, ………12分
所以原不等式的解集为………14分
17、(本题满分15分)
解:(1)函数的图象
当时,
取点和,得射线;……3分
对,取点和
函数的图象如图所示。………7分
注:时的图象,未经过整点和的,扣1分;画到x轴下方的,扣1分,图象上凸画成上凹的,此段不得分,即扣4分。
射线部分,画成不经过整点和的,扣1分,点画成实点的,扣1分;
【建议】:教学中要强化对画图象的规范要求。教师示范,适当练习。
(2)任取,设,…………9分
因为
则 …………11分
而 又 …………13分
所以, 即: …………14分
所以函数在上为减函数. …………15分
18、(本题满分15分)
解:(1)设,所以,
,
…………2分
∴ …………4分
由条件得,
∴函数的解析式 …………7分
(2)函数 ,的图象如图所示 …………10分
当直线与图角的交点情况是:
当时,只有一个交点;
当时,有两个交点;
当时,只有一个交点;…………14分
所以,方程在区间上只有一个实数根,
此时或 …………15分
另解:
方程可化为:
当时,有两个实根: ………10分
时,
时,, 此时方程在区间上有两个根。
时,,此时方程在区间上只有一个根………14分
所以,若方程在区间上只有一个实数根,
的取值范围是。………15分
说明:用代数法讨论时,如果将两个相等的根,不认为是一个根,则不扣分。事实上,用代数法讨论时,注意到对称轴是,则大根在区间内,小根必在;小根不在区间,大根则必不在,这样讨论会很清晰。
19、(本题满分16分)
解:(1)由题意:当0≤x≤20时,v(x)=60;…………………2分
当20≤x≤200时,设v(x)=kx+b,
再由已知,得解得 …………………5分
故函数v(x)的表达式为…………………7分
(2)依题意并由(1)可得 …………………9分
当0≤x≤20时,f(x)为增函数,
故当x=20时,其最大值为60×20=1200; ………………… 11分
当20<x≤200时,f(x)=x(200-x) =
所以当且仅当x=100时,f(x) 最大值为
所以,当x=100时,f(x)在区间(20,200]上取得最大值 . ……14分
综上,当x=100时,f(x)在区间[0,200]上取得最大值≈3333,. ……15分
答:当车流密度为100 辆/千米时,车流量可以达到最大,最大值约为3333辆/小时.……………16分 .
20、(本题满分16分)
解:(1)因为,函数为偶函数.
由,得x(+a)=-x(+a),…………3分
2a=-(+)=1,…………5分
解得,a= 经检验 a=符合题意. …………7分
注:若由特殊值求出a=,一定要检验是否恒成立。否则扣3分.
(2)恒成立对恒成立,
∴
∴ …………8分
∵+在[1,3]上为减函数, …………10分
∴对恒成立 …………13分
∴ …………15分
所以m的取值范围是 …………16分
-2
-1
1
1
-2
-1
1
1
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
同课章节目录
