沪科版八年级数学上册试题 第14章全等三角形 单元测试(含答案)
文档属性
| 名称 | 沪科版八年级数学上册试题 第14章全等三角形 单元测试(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1012.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-16 16:19:20 | ||
图片预览




文档简介
第14章全等三角形单元测试
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.下列说法正确的是
A.三个角对应相等的两个三角形全等
B.两角对应相等,且一条边也对应相等的两个三角形全等
C.两边和其中一边的对角对应相等的两个三角形全等
D.有两个角与一边相等的两个三角形不一定全等
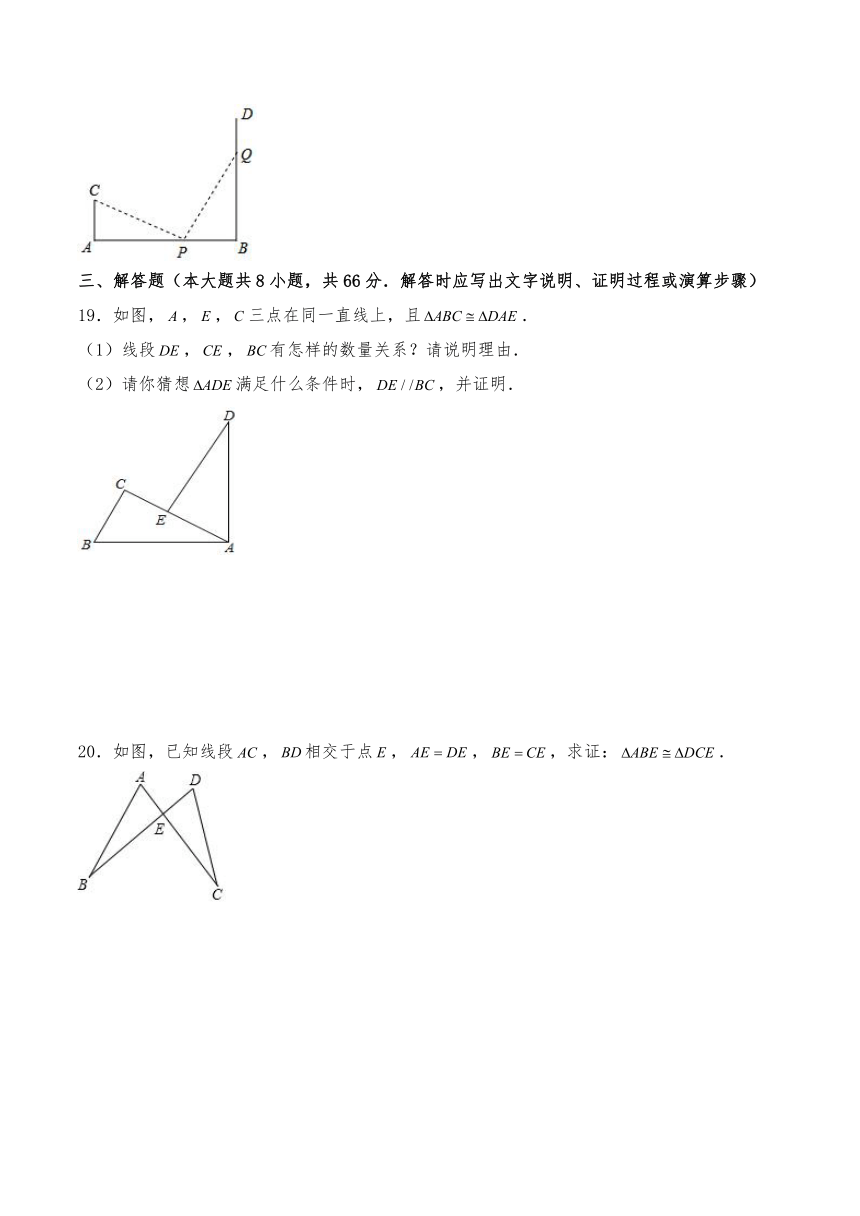
2.如图,,,要得到,只需添加
A. B. C. D.
3.如图,要测池塘两端,的距离,小明先在地上取一个可以直接到达和的点,连接并延长到,使;连接并延长到,使,连接并测量出它的长度,的长度就是,间的距离.那么判定和全等的依据是
A. B. C. D.
4.如图,在中,的垂直平分线交于点,交于点,连接.若,的周长为13,则的周长为
A.19 B.16 C.29 D.18
5.如图,在中,平分,,,,则的长为
A.3 B.11 C.15 D.9
6.如图,有一块三角形玻璃,小明不小心将它打破.带上这块玻璃,能配成同样大小的一块,其理由是
A. B. C. D.
7.下列判断正确的个数是
①三角形的三条高都在三角形的内部,并且相交于一点;②两边及一角对应相等的两个三角形全等;③两角及一边对应相等的两个三角形全等;④到三角形的三边所在的直线距离相等的点有三个;⑤两边及第三边上的高对应相等的两个三角形全等.
A.4 B.3 C.2 D.1
8.如图,在与中,,,,.若,下列结论正确的是
A. B. C. D.
9.如图,在和中,点、、在同一直线上,已知,,添加以下条件后,仍不能判定的是
A. B. C. D.
10.如图,在和中,,,与相交于点,与相交于点,与相交于点,.有下列结论:①;②;③;④.其中正确结论的个数是
A.1个 B.2个 C.3个 D.4个
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.已知,,,则 .
12.如图,已知,,请你添加一个条件,使得,你添加的条件是 .(不添加任何字母和辅助线)
13.如图,、相交于点,,请你补充一个条件,使得,你补充的条件是 .
14.如图,点是的角平分线上一点,分别连接、,添加一个条件就可以判定,这个条件是 .
15.如图,,,则 .
16.在中,是边上的中线,若,,则长的取值范围是 .
17.如图,已知,,添加下列哪个条件可以利用判断.正确的是: .
①;②;
③;④.
18.如图,,于,于,且,点从向运动,速度为,点从向运动,速度为,、两点同时出发,运动 秒后与全等.
三、解答题(本大题共8小题,共66分.解答时应写出文字说明、证明过程或演算步骤)
19.如图,,,三点在同一直线上,且.
(1)线段,,有怎样的数量关系?请说明理由.
(2)请你猜想满足什么条件时,,并证明.
20.如图,已知线段,相交于点,,,求证:.
21.如图,中,既是中线,又是角平分线,于点,于点.
(1)求证:;
(2)你认为还是的高吗?如果是,请给出证明;如果不是,请说明理由.
22.李华同学用11块高度都是的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个正方形,点在上,点和分别与木墙的顶端重合,求两堵木墙之间的距离.
23.如图所示,,,三点在同一直线上,且.
(1)求证:;
(2)当满足什么条件时,?
24.已知:点、、、在同一条直线上,,,.
(1)如图1,求证:.
(2)如图2,连接、、、,在不添加任何辅助线的情况下,请直接写出图2中所有全等的三角形(除全等于外).
25.如图,在中,,分别是,边上的高,在上截取,延长至点使,连接,.
(1)如图1,求证:;
(2)如图2,若恰好平分,过点作交的延长线于点,请直接写出图中所有的全等三角形并用全等符号连接.
26.如图,在长方形中,,,点从点出发,以秒的速度沿向点运动,设点的运动时间为秒:
(1) .(用的代数式表示)
(2)当为何值时,?
(3)当点从点开始运动,同时,点从点出发,以秒的速度沿向点运动,是否存在这样的值,使得与全等?若存在,请求出的值;若不存在,请说明理由.
答案
一、选择题
..........
二、填空题
11..
12.或或.
13..
14.
15..
16..
17.②.
18.4.
三、解答题
19.(1)解:.
理由:,
,.
,,三点在同一直线上,
,
;
(2)猜想:,
则.
,
,
.
又,
,
当满足时,.
20.证明:在和中
,
21.(1)证明:既是中线,又是角平分线,,,
,,,
在和中,
,
;
(2)还是的高,
证明:由(1),
,
既是中线,又是角平分线,
,,
在和中,
,
,
,
,
,
即还是的高.
22.解:,,
,
,
,
,
,
在和中,
,
,
,,
.
23.(1)证明:,
,,
又,
;
(2)解:,
,
又,
,
,
又,
,
即当满足为直角时,.
24.(1)证明:,
,
即,
,
,
在和中
,
;
(2)图2中的全等三角形有,,,,,
理由是:,
,,
在和中
,
,
,,
在和中
,
,
,
在和中
,
,
在和中
,
,
,
在和中
,
.
25.证明:(1)、分别是、两条边上的高,
,
,
,
在与中,,
,
;
(2)图中全等三角形有,由得出,
由得出,;.
26.解:(1)点从点出发,以秒的速度沿向点运动,点的运动时间为秒时,,
则;
故答案为:;
(2)当时,
则,
故,
解得:;
(3)①如图1,当,则,,
,
,
,
解得:,
,
,
解得:秒).
②如图2,当,则,.
,
,
,
,
解得:,
,
,
解得:;
综上所述:当秒或秒时与全等.
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.下列说法正确的是
A.三个角对应相等的两个三角形全等
B.两角对应相等,且一条边也对应相等的两个三角形全等
C.两边和其中一边的对角对应相等的两个三角形全等
D.有两个角与一边相等的两个三角形不一定全等
2.如图,,,要得到,只需添加
A. B. C. D.
3.如图,要测池塘两端,的距离,小明先在地上取一个可以直接到达和的点,连接并延长到,使;连接并延长到,使,连接并测量出它的长度,的长度就是,间的距离.那么判定和全等的依据是
A. B. C. D.
4.如图,在中,的垂直平分线交于点,交于点,连接.若,的周长为13,则的周长为
A.19 B.16 C.29 D.18
5.如图,在中,平分,,,,则的长为
A.3 B.11 C.15 D.9
6.如图,有一块三角形玻璃,小明不小心将它打破.带上这块玻璃,能配成同样大小的一块,其理由是
A. B. C. D.
7.下列判断正确的个数是
①三角形的三条高都在三角形的内部,并且相交于一点;②两边及一角对应相等的两个三角形全等;③两角及一边对应相等的两个三角形全等;④到三角形的三边所在的直线距离相等的点有三个;⑤两边及第三边上的高对应相等的两个三角形全等.
A.4 B.3 C.2 D.1
8.如图,在与中,,,,.若,下列结论正确的是
A. B. C. D.
9.如图,在和中,点、、在同一直线上,已知,,添加以下条件后,仍不能判定的是
A. B. C. D.
10.如图,在和中,,,与相交于点,与相交于点,与相交于点,.有下列结论:①;②;③;④.其中正确结论的个数是
A.1个 B.2个 C.3个 D.4个
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.已知,,,则 .
12.如图,已知,,请你添加一个条件,使得,你添加的条件是 .(不添加任何字母和辅助线)
13.如图,、相交于点,,请你补充一个条件,使得,你补充的条件是 .
14.如图,点是的角平分线上一点,分别连接、,添加一个条件就可以判定,这个条件是 .
15.如图,,,则 .
16.在中,是边上的中线,若,,则长的取值范围是 .
17.如图,已知,,添加下列哪个条件可以利用判断.正确的是: .
①;②;
③;④.
18.如图,,于,于,且,点从向运动,速度为,点从向运动,速度为,、两点同时出发,运动 秒后与全等.
三、解答题(本大题共8小题,共66分.解答时应写出文字说明、证明过程或演算步骤)
19.如图,,,三点在同一直线上,且.
(1)线段,,有怎样的数量关系?请说明理由.
(2)请你猜想满足什么条件时,,并证明.
20.如图,已知线段,相交于点,,,求证:.
21.如图,中,既是中线,又是角平分线,于点,于点.
(1)求证:;
(2)你认为还是的高吗?如果是,请给出证明;如果不是,请说明理由.
22.李华同学用11块高度都是的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个正方形,点在上,点和分别与木墙的顶端重合,求两堵木墙之间的距离.
23.如图所示,,,三点在同一直线上,且.
(1)求证:;
(2)当满足什么条件时,?
24.已知:点、、、在同一条直线上,,,.
(1)如图1,求证:.
(2)如图2,连接、、、,在不添加任何辅助线的情况下,请直接写出图2中所有全等的三角形(除全等于外).
25.如图,在中,,分别是,边上的高,在上截取,延长至点使,连接,.
(1)如图1,求证:;
(2)如图2,若恰好平分,过点作交的延长线于点,请直接写出图中所有的全等三角形并用全等符号连接.
26.如图,在长方形中,,,点从点出发,以秒的速度沿向点运动,设点的运动时间为秒:
(1) .(用的代数式表示)
(2)当为何值时,?
(3)当点从点开始运动,同时,点从点出发,以秒的速度沿向点运动,是否存在这样的值,使得与全等?若存在,请求出的值;若不存在,请说明理由.
答案
一、选择题
..........
二、填空题
11..
12.或或.
13..
14.
15..
16..
17.②.
18.4.
三、解答题
19.(1)解:.
理由:,
,.
,,三点在同一直线上,
,
;
(2)猜想:,
则.
,
,
.
又,
,
当满足时,.
20.证明:在和中
,
21.(1)证明:既是中线,又是角平分线,,,
,,,
在和中,
,
;
(2)还是的高,
证明:由(1),
,
既是中线,又是角平分线,
,,
在和中,
,
,
,
,
,
即还是的高.
22.解:,,
,
,
,
,
,
在和中,
,
,
,,
.
23.(1)证明:,
,,
又,
;
(2)解:,
,
又,
,
,
又,
,
即当满足为直角时,.
24.(1)证明:,
,
即,
,
,
在和中
,
;
(2)图2中的全等三角形有,,,,,
理由是:,
,,
在和中
,
,
,,
在和中
,
,
,
在和中
,
,
在和中
,
,
,
在和中
,
.
25.证明:(1)、分别是、两条边上的高,
,
,
,
在与中,,
,
;
(2)图中全等三角形有,由得出,
由得出,;.
26.解:(1)点从点出发,以秒的速度沿向点运动,点的运动时间为秒时,,
则;
故答案为:;
(2)当时,
则,
故,
解得:;
(3)①如图1,当,则,,
,
,
,
解得:,
,
,
解得:秒).
②如图2,当,则,.
,
,
,
,
解得:,
,
,
解得:;
综上所述:当秒或秒时与全等.
