沪科版八年级数学上册试题第14章 《全等三角形》 一课一练(含答案)
文档属性
| 名称 | 沪科版八年级数学上册试题第14章 《全等三角形》 一课一练(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 184.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-16 09:11:33 | ||
图片预览



文档简介
《全等三角形》
一、选择题
1.一块三角形玻璃样板不慎被张字同学碰破,成了四片完整碎片(如图所示),聪明的他经过仔细地考虑认为只要带其中的两块碎片去玻璃店就可以让师傅画一块与以前一样的玻璃样板,你认为下列四个答案中考虑最全面的是( )
A.带1,2或2,3去就可以了
B.带1,4或3,4去就可以了
C.带1,4或2,4或3,4去均可
D.带其中的任意两块去都可以
2.如图,有两个长度相同的滑梯靠在一面墙的两侧,已知左边滑梯的高度AC与右边滑梯水平方向的宽度DF相等,则这两个滑梯与墙面的夹角∠ACB与∠DEF的度数和为( )
A.60° B.75° C.90° D.120°
3.如图,有两个长度相同的滑梯靠在一面墙上.已知左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,则这两个滑梯与地面夹角∠ABC与∠DFE的度数和是( )
A.60° B.90° C.120° D.150°
4.如图,为了测量B点到河对面的目标A之间的距离,在B点同侧选择了一点C,测得∠ABC=75°,∠ACB=35°,然后在M处立了标杆,使∠CBM=75°,∠MCB=35°,得到△MBC≌△ABC,所以测得MB的长就是A,B两点间的距离,这里判定△MBC≌△ABC的理由是( )
A.SAS B.AAA C.SSS D.ASA
5.如图,要测量河两岸相对的两点A、B的距离,先在AB的垂线BF上取两点C、D,使BC=CD,再作出BF的垂线DE,使点A、C、E在同一条直线上(如图),可以说明△ABC≌△EDC,得AB=DE,因此测得DE的长就是AB的长,判定△ABC≌△EDC,最恰当的理由是( )
A.SAS B.HL C.SSS D.ASA
6.在测量一个小口圆柱形容器的壁厚时,小明用“X型转动钳”按如图方法进行测量,其中OA=OD,OB=OC,AD=BC,测得AB=a,EF=b,圆柱形容器的壁厚是( )
A.a B.b C.b﹣a D.(b﹣a)
7.工人师傅常用角尺平分一个任意角,做法如下:如图,∠AOB是一个任意角,在边OA、OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与点M、N重合,过角尺顶点C作射线OC,由此作法便可得△NOC≌△MOC,其依据是( )
A.SSS B.SAS C.ASA D.AAS
8.如图,把两根钢条AA′、BB′的中点连在一起,可以做成一个测量工件内槽宽的工具(卡钳),若测得AB=5米,则槽宽为( )
A.3 B.4 C.5 D.6
9.已知△ABC≌△DEF,BC=EF=6cm,△ABC的面积为18平方厘米,则EF边上的高是( )
A.6cm B.7cm C.8cm D.9cm
10.如图,将一根笔直的竹竿斜放在竖直墙角AOB中,初始位置为CD,当一端C下滑至C'时,另一端D向右滑到D',则下列说法正确的是( )
A.下滑过程中,始终有CC'=DD'
B.下滑过程中,始终有CC'≠DD'
C.若OC<OD,则下滑过程中,一定存在某个位置使得CC'=DD'
D.若OC>OD,则下滑过程中,一定存在某个位置使得CC'=DD'
二、填空题
11.如图,AC=DB,AO=DO,CD=20m,则A,B两点间的距离为 m.
12.如图,某人将一块三角形玻璃打碎成两块,带 块(填序号)能到玻璃店配一块完全一样的玻璃,用到的数学道理是 .
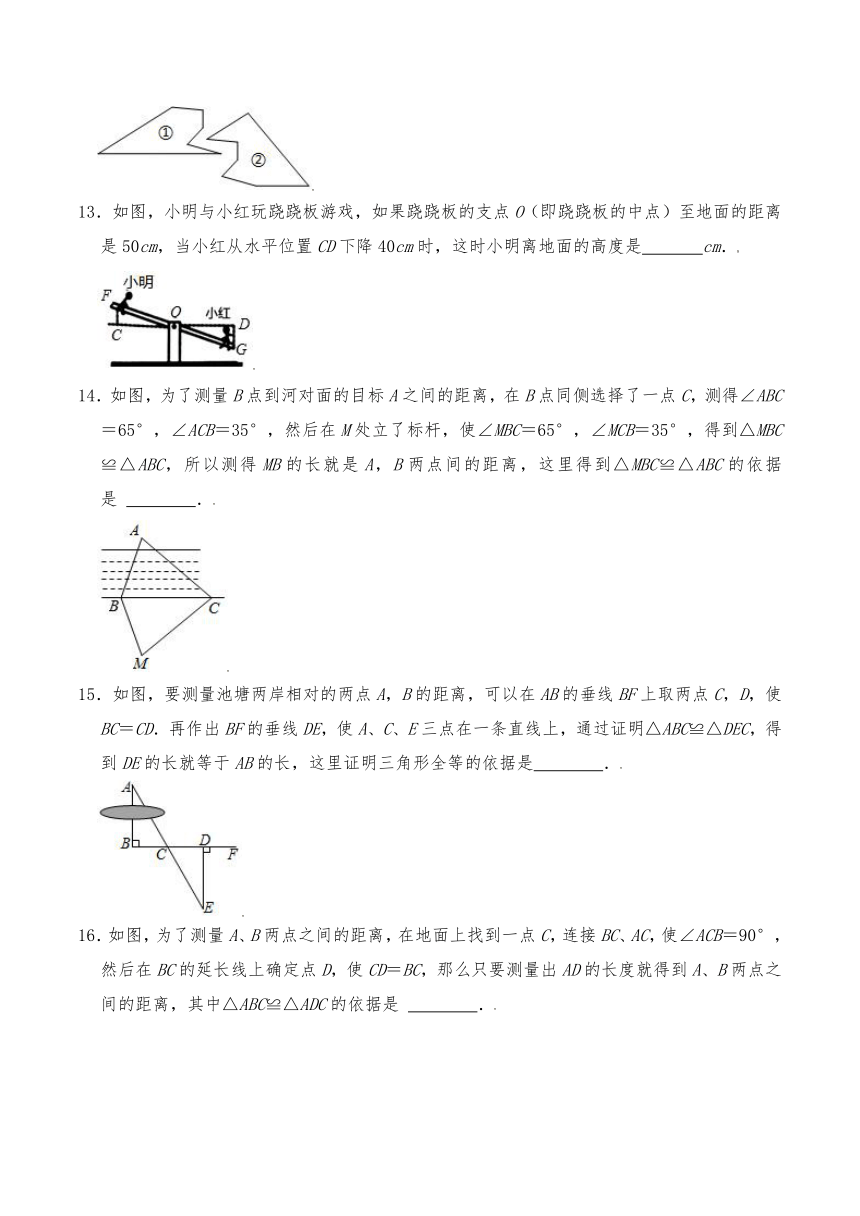
13.如图,小明与小红玩跷跷板游戏,如果跷跷板的支点O(即跷跷板的中点)至地面的距离是50cm,当小红从水平位置CD下降40cm时,这时小明离地面的高度是 cm.
14.如图,为了测量B点到河对面的目标A之间的距离,在B点同侧选择了一点C,测得∠ABC=65°,∠ACB=35°,然后在M处立了标杆,使∠MBC=65°,∠MCB=35°,得到△MBC≌△ABC,所以测得MB的长就是A,B两点间的距离,这里得到△MBC≌△ABC的依据是 .
15.如图,要测量池塘两岸相对的两点A,B的距离,可以在AB的垂线BF上取两点C,D,使BC=CD.再作出BF的垂线DE,使A、C、E三点在一条直线上,通过证明△ABC≌△DEC,得到DE的长就等于AB的长,这里证明三角形全等的依据是 .
16.如图,为了测量A、B两点之间的距离,在地面上找到一点C,连接BC、AC,使∠ACB=90°,然后在BC的延长线上确定点D,使CD=BC,那么只要测量出AD的长度就得到A、B两点之间的距离,其中△ABC≌△ADC的依据是 .
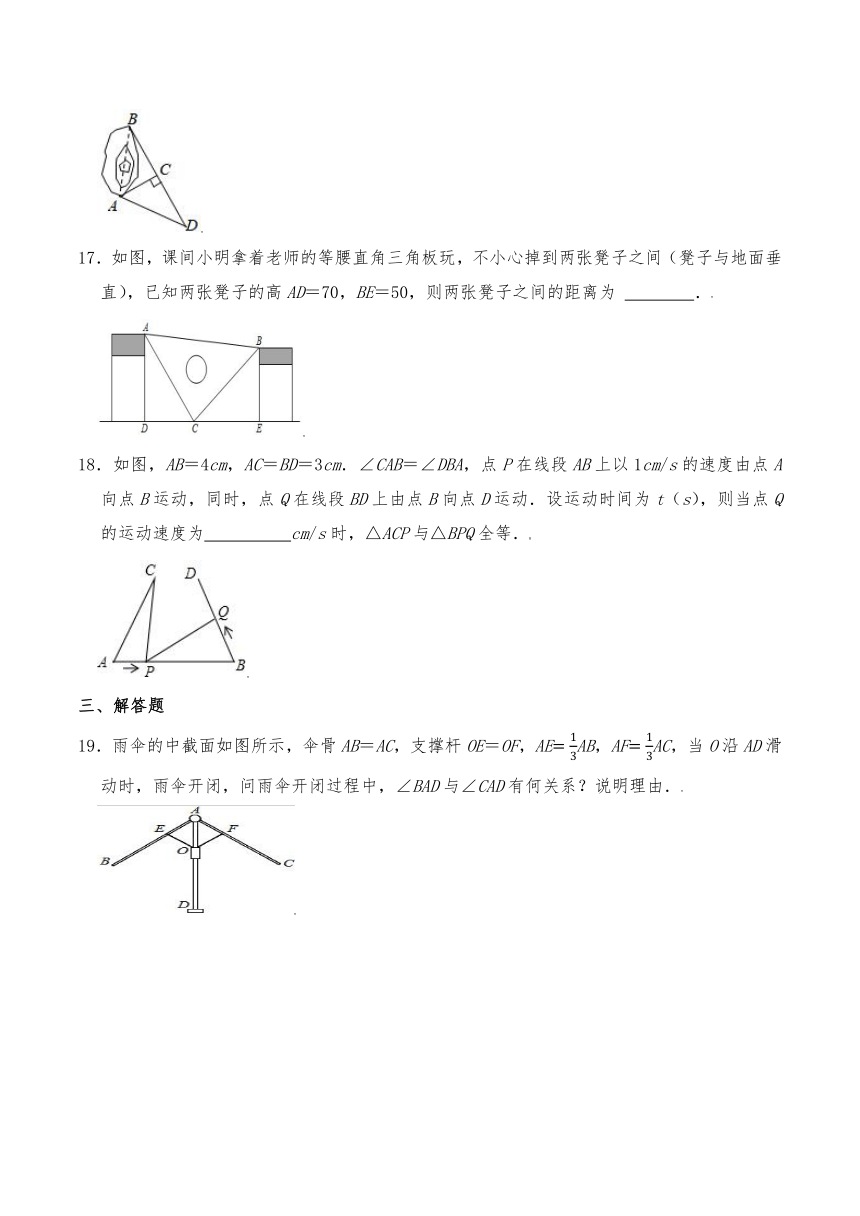
17.如图,课间小明拿着老师的等腰直角三角板玩,不小心掉到两张凳子之间(凳子与地面垂直),已知两张凳子的高AD=70,BE=50,则两张凳子之间的距离为 .
18.如图,AB=4cm,AC=BD=3cm.∠CAB=∠DBA,点P在线段AB上以1cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动.设运动时间为t(s),则当点Q的运动速度为 cm/s时,△ACP与△BPQ全等.
三、解答题
19.雨伞的中截面如图所示,伞骨AB=AC,支撑杆OE=OF,AEAB,AFAC,当O沿AD滑动时,雨伞开闭,问雨伞开闭过程中,∠BAD与∠CAD有何关系?说明理由.
20.小明与爸爸妈妈在公园里荡秋千,如图,小明坐在秋千的起始位置A处,OA与地面垂直,两脚在地面上用力一蹬,妈妈在距地面1.2m高的B处接住他后用力一推,爸爸在C处接住他,若妈妈与爸爸到OA的水平距离BD、CE分别为1.6m和2m,∠BOC=90°.
(1)△OBD与△COE全等吗?请说明理由;
(2)爸爸是在距离地面多高的地方接住小明的?
21.如图,点B、F、C、E在直线l上(F、C之间不能直接测量),点A、D在l异侧,测得AB=DE,AB∥DE,∠A=∠D.
(1)求证:△ABC≌△DEF;
(2)若BE=10m,BF=3m,求FC的长度.
22.如图,要测量河两岸相对两点A、B间的距离,在河岸BM上截取BC=CD,作ED⊥BD交AC的延长线于点E,垂足为点D.(DE≠CD)
(1)线段 的长度就是A、B两点间的距离
(2)请说明(1)成立的理由.
23.某中学计划为新生配备如图1所示的折叠凳,图2是折叠凳撑开后的侧面示意图(木条等材料宽度忽略不计),其中凳腿AB和CD的长度相等,O是它们的中点,为了使折叠凳坐着舒适,厂家将撑开后的折叠凳宽度AD设计为35cm,由以上信息能求出CB的长度吗?如果能,请求出CB的长度;如果不能,请说明理由.
24.一位经历过战争的老战士讲述了这样一个故事:在一次战役中,我军阵地与敌军碉堡隔河相望.为了炸掉这个碉堡,需要知道碉堡与我军阵地的距离,在不能过河测量又没有任何测量工具的情况下,一个战士想出来这样的办法:他面向碉堡的方向站好,然后调整帽子,使视线通过帽檐正好落在碉堡的底部;然后,他转过一个角度,保持刚才的姿态,这时视线落在了自己所在岸的某一点上,接着,他用步测的方法量出自己与那个点的距离,这个距离就是他与碉堡间的距离.
将这位战士看成一条线段,碉堡看成一点,示意图如下,你能根据示意图解释其中的道理吗
下面是彤彤同学写出的不完整的已知和求证,请你补全已知和求证,并完成证明.
已知:如图,AB⊥CD, .
求证: .
证明:
答案
一、选择题
C.C.B.D.D.D.A.C.A.D.
二、填空题
11.20.
12.②,ASA.
13.90.
14.ASA.
15.ASA.
16.SAS.
17.120.
18.1或1.5.
三、解答题
19.解:雨伞开闭过程中二者关系始终是:∠BAD=∠CAD,
理由如下:
∵AB=AC,AEAB,AFAC,
∴AE=AF,
在△AOE与△AOF中,
,
∴△AOE≌△AOF(SSS),
∴∠BAD=∠CAD.
20.解:(1)△OBD与△COE全等.
理由如下:
由题意可知∠CEO=∠BDO=90°,OB=OC,
∵∠BOC=90°,
∴∠COE+∠BOD=∠BOD+∠OBD=90°.
∴∠COE=∠OBD,
在△COE和△OBD中,
,
∴△COE≌△OBD(AAS);
(2)∵△COE≌△OBD,
∴CE=OD,OE=BD,
∵BD、CE分别为1.6m和2m,
∴DE=OD﹣OE=CE﹣BD=2﹣1.6=0.4(m),
∵AD=1.2m,
∴AE=AD+DE=1.6(m),
答:爸爸是在距离地面1.6m的地方接住小明的.
21.(1)证明:∵AB∥DE,
∴∠ABC=∠DEF,
在△ABC与△DEF中
∴△ABC≌△DEF;
(2)∵△ABC≌△DEF,
∴BC=EF,
∴BF+FC=EC+FC,
∴BF=EC,
∵BE=10m,BF=3m,
∴FC=10﹣3﹣3=4m.
22.解:(1)线段DE的长度就是A、B两点间的距离;
故答案为:DE;
(2)∵AB⊥BC,DE⊥BD
∴∠ABC=∠EDC=90°
又∵∠ACB=∠DCE,BC=CD
∴△ABC≌△CDE(ASA)
∴AB=DE.
23.解:∵O是AB、CD的中点,
∴OA=OB,OC=OD,
在△AOD和△BOC中,
,
∴△AOD≌△BOC(SAS),
∴CB=AD,
∵AD=35cm,
∴CB=35(cm),
答:CB的长度为35cm.
24.解:已知:如图,AB⊥CD,∠ABC=∠ABD.
求证:AD=AC.
证明:∵AB⊥CD,
∴∠BAD=∠BAC,
在△ABD与△ABC中,
,
∴△ABD≌△ABC(ASA),
∴AD=AC,
故答案为:∠ABC=∠ABD,AD=AC.
一、选择题
1.一块三角形玻璃样板不慎被张字同学碰破,成了四片完整碎片(如图所示),聪明的他经过仔细地考虑认为只要带其中的两块碎片去玻璃店就可以让师傅画一块与以前一样的玻璃样板,你认为下列四个答案中考虑最全面的是( )
A.带1,2或2,3去就可以了
B.带1,4或3,4去就可以了
C.带1,4或2,4或3,4去均可
D.带其中的任意两块去都可以
2.如图,有两个长度相同的滑梯靠在一面墙的两侧,已知左边滑梯的高度AC与右边滑梯水平方向的宽度DF相等,则这两个滑梯与墙面的夹角∠ACB与∠DEF的度数和为( )
A.60° B.75° C.90° D.120°
3.如图,有两个长度相同的滑梯靠在一面墙上.已知左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,则这两个滑梯与地面夹角∠ABC与∠DFE的度数和是( )
A.60° B.90° C.120° D.150°
4.如图,为了测量B点到河对面的目标A之间的距离,在B点同侧选择了一点C,测得∠ABC=75°,∠ACB=35°,然后在M处立了标杆,使∠CBM=75°,∠MCB=35°,得到△MBC≌△ABC,所以测得MB的长就是A,B两点间的距离,这里判定△MBC≌△ABC的理由是( )
A.SAS B.AAA C.SSS D.ASA
5.如图,要测量河两岸相对的两点A、B的距离,先在AB的垂线BF上取两点C、D,使BC=CD,再作出BF的垂线DE,使点A、C、E在同一条直线上(如图),可以说明△ABC≌△EDC,得AB=DE,因此测得DE的长就是AB的长,判定△ABC≌△EDC,最恰当的理由是( )
A.SAS B.HL C.SSS D.ASA
6.在测量一个小口圆柱形容器的壁厚时,小明用“X型转动钳”按如图方法进行测量,其中OA=OD,OB=OC,AD=BC,测得AB=a,EF=b,圆柱形容器的壁厚是( )
A.a B.b C.b﹣a D.(b﹣a)
7.工人师傅常用角尺平分一个任意角,做法如下:如图,∠AOB是一个任意角,在边OA、OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与点M、N重合,过角尺顶点C作射线OC,由此作法便可得△NOC≌△MOC,其依据是( )
A.SSS B.SAS C.ASA D.AAS
8.如图,把两根钢条AA′、BB′的中点连在一起,可以做成一个测量工件内槽宽的工具(卡钳),若测得AB=5米,则槽宽为( )
A.3 B.4 C.5 D.6
9.已知△ABC≌△DEF,BC=EF=6cm,△ABC的面积为18平方厘米,则EF边上的高是( )
A.6cm B.7cm C.8cm D.9cm
10.如图,将一根笔直的竹竿斜放在竖直墙角AOB中,初始位置为CD,当一端C下滑至C'时,另一端D向右滑到D',则下列说法正确的是( )
A.下滑过程中,始终有CC'=DD'
B.下滑过程中,始终有CC'≠DD'
C.若OC<OD,则下滑过程中,一定存在某个位置使得CC'=DD'
D.若OC>OD,则下滑过程中,一定存在某个位置使得CC'=DD'
二、填空题
11.如图,AC=DB,AO=DO,CD=20m,则A,B两点间的距离为 m.
12.如图,某人将一块三角形玻璃打碎成两块,带 块(填序号)能到玻璃店配一块完全一样的玻璃,用到的数学道理是 .
13.如图,小明与小红玩跷跷板游戏,如果跷跷板的支点O(即跷跷板的中点)至地面的距离是50cm,当小红从水平位置CD下降40cm时,这时小明离地面的高度是 cm.
14.如图,为了测量B点到河对面的目标A之间的距离,在B点同侧选择了一点C,测得∠ABC=65°,∠ACB=35°,然后在M处立了标杆,使∠MBC=65°,∠MCB=35°,得到△MBC≌△ABC,所以测得MB的长就是A,B两点间的距离,这里得到△MBC≌△ABC的依据是 .
15.如图,要测量池塘两岸相对的两点A,B的距离,可以在AB的垂线BF上取两点C,D,使BC=CD.再作出BF的垂线DE,使A、C、E三点在一条直线上,通过证明△ABC≌△DEC,得到DE的长就等于AB的长,这里证明三角形全等的依据是 .
16.如图,为了测量A、B两点之间的距离,在地面上找到一点C,连接BC、AC,使∠ACB=90°,然后在BC的延长线上确定点D,使CD=BC,那么只要测量出AD的长度就得到A、B两点之间的距离,其中△ABC≌△ADC的依据是 .
17.如图,课间小明拿着老师的等腰直角三角板玩,不小心掉到两张凳子之间(凳子与地面垂直),已知两张凳子的高AD=70,BE=50,则两张凳子之间的距离为 .
18.如图,AB=4cm,AC=BD=3cm.∠CAB=∠DBA,点P在线段AB上以1cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动.设运动时间为t(s),则当点Q的运动速度为 cm/s时,△ACP与△BPQ全等.
三、解答题
19.雨伞的中截面如图所示,伞骨AB=AC,支撑杆OE=OF,AEAB,AFAC,当O沿AD滑动时,雨伞开闭,问雨伞开闭过程中,∠BAD与∠CAD有何关系?说明理由.
20.小明与爸爸妈妈在公园里荡秋千,如图,小明坐在秋千的起始位置A处,OA与地面垂直,两脚在地面上用力一蹬,妈妈在距地面1.2m高的B处接住他后用力一推,爸爸在C处接住他,若妈妈与爸爸到OA的水平距离BD、CE分别为1.6m和2m,∠BOC=90°.
(1)△OBD与△COE全等吗?请说明理由;
(2)爸爸是在距离地面多高的地方接住小明的?
21.如图,点B、F、C、E在直线l上(F、C之间不能直接测量),点A、D在l异侧,测得AB=DE,AB∥DE,∠A=∠D.
(1)求证:△ABC≌△DEF;
(2)若BE=10m,BF=3m,求FC的长度.
22.如图,要测量河两岸相对两点A、B间的距离,在河岸BM上截取BC=CD,作ED⊥BD交AC的延长线于点E,垂足为点D.(DE≠CD)
(1)线段 的长度就是A、B两点间的距离
(2)请说明(1)成立的理由.
23.某中学计划为新生配备如图1所示的折叠凳,图2是折叠凳撑开后的侧面示意图(木条等材料宽度忽略不计),其中凳腿AB和CD的长度相等,O是它们的中点,为了使折叠凳坐着舒适,厂家将撑开后的折叠凳宽度AD设计为35cm,由以上信息能求出CB的长度吗?如果能,请求出CB的长度;如果不能,请说明理由.
24.一位经历过战争的老战士讲述了这样一个故事:在一次战役中,我军阵地与敌军碉堡隔河相望.为了炸掉这个碉堡,需要知道碉堡与我军阵地的距离,在不能过河测量又没有任何测量工具的情况下,一个战士想出来这样的办法:他面向碉堡的方向站好,然后调整帽子,使视线通过帽檐正好落在碉堡的底部;然后,他转过一个角度,保持刚才的姿态,这时视线落在了自己所在岸的某一点上,接着,他用步测的方法量出自己与那个点的距离,这个距离就是他与碉堡间的距离.
将这位战士看成一条线段,碉堡看成一点,示意图如下,你能根据示意图解释其中的道理吗
下面是彤彤同学写出的不完整的已知和求证,请你补全已知和求证,并完成证明.
已知:如图,AB⊥CD, .
求证: .
证明:
答案
一、选择题
C.C.B.D.D.D.A.C.A.D.
二、填空题
11.20.
12.②,ASA.
13.90.
14.ASA.
15.ASA.
16.SAS.
17.120.
18.1或1.5.
三、解答题
19.解:雨伞开闭过程中二者关系始终是:∠BAD=∠CAD,
理由如下:
∵AB=AC,AEAB,AFAC,
∴AE=AF,
在△AOE与△AOF中,
,
∴△AOE≌△AOF(SSS),
∴∠BAD=∠CAD.
20.解:(1)△OBD与△COE全等.
理由如下:
由题意可知∠CEO=∠BDO=90°,OB=OC,
∵∠BOC=90°,
∴∠COE+∠BOD=∠BOD+∠OBD=90°.
∴∠COE=∠OBD,
在△COE和△OBD中,
,
∴△COE≌△OBD(AAS);
(2)∵△COE≌△OBD,
∴CE=OD,OE=BD,
∵BD、CE分别为1.6m和2m,
∴DE=OD﹣OE=CE﹣BD=2﹣1.6=0.4(m),
∵AD=1.2m,
∴AE=AD+DE=1.6(m),
答:爸爸是在距离地面1.6m的地方接住小明的.
21.(1)证明:∵AB∥DE,
∴∠ABC=∠DEF,
在△ABC与△DEF中
∴△ABC≌△DEF;
(2)∵△ABC≌△DEF,
∴BC=EF,
∴BF+FC=EC+FC,
∴BF=EC,
∵BE=10m,BF=3m,
∴FC=10﹣3﹣3=4m.
22.解:(1)线段DE的长度就是A、B两点间的距离;
故答案为:DE;
(2)∵AB⊥BC,DE⊥BD
∴∠ABC=∠EDC=90°
又∵∠ACB=∠DCE,BC=CD
∴△ABC≌△CDE(ASA)
∴AB=DE.
23.解:∵O是AB、CD的中点,
∴OA=OB,OC=OD,
在△AOD和△BOC中,
,
∴△AOD≌△BOC(SAS),
∴CB=AD,
∵AD=35cm,
∴CB=35(cm),
答:CB的长度为35cm.
24.解:已知:如图,AB⊥CD,∠ABC=∠ABD.
求证:AD=AC.
证明:∵AB⊥CD,
∴∠BAD=∠BAC,
在△ABD与△ABC中,
,
∴△ABD≌△ABC(ASA),
∴AD=AC,
故答案为:∠ABC=∠ABD,AD=AC.
