沪科版八年级数学上册试题 15.1轴对称图形-一课一练(含答案)
文档属性
| 名称 | 沪科版八年级数学上册试题 15.1轴对称图形-一课一练(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 193.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-16 00:00:00 | ||
图片预览



文档简介
15.1轴对称图形
一、选择题
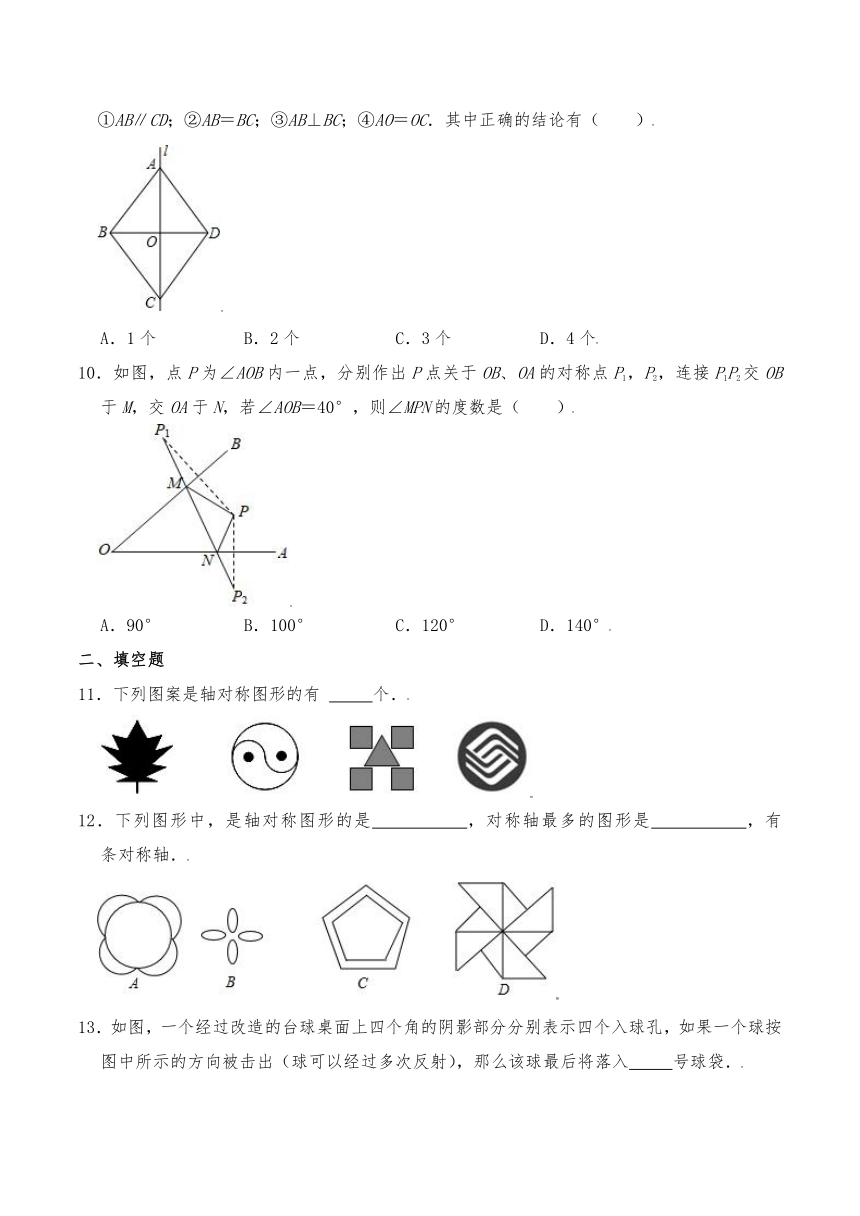
1.2020年的春节,对于所有人来说真的不一般.为了打好疫情攻坚战,医护人员在岗位上同时间赛跑,与病魔较量,而我们每个人都能为打赢这场仗贡献一份力量.勤洗手,戴口罩,少聚会,积极配合;防控工作,照顾好自己和家人,还有,说出一句简单的:中国加油!武汉加油!在“中国加油”这4个美术字中,可以看作轴对称图形的是( )
A.中 B.国 C.加 D.油
2.下列古钱币图案中,轴对称图形的个数是( )
A.1 B.2 C.3 D.4
3.下列微信表情图标属于轴对称图形的是( )
A. B. C. D.
4.剪纸是我国传统的民间艺术.将一张纸片按图中①,②的方式沿虚线依次对折后,再沿图③中的虚线裁剪,最后将图④中的纸片打开铺平,所得图案应该是( )
A. B. C. D.
5.如图,△ABC与△A′B′C′关于直线l对称,且∠A=102°,∠C′=25°,则∠B的度数为( )
A.35° B.53° C.63° D.43°
6.如图,若△ABC与△A'B'C'关于直线MN对称,BB'交MN于点O,则下列说法中,不一定正确的是( )
A.AC=A'C' B.AB∥B'C' C.AA'⊥MN D.BO=B'O
7.如图,△ABC与△DEF关于直线l对称,BE交l于点O,则下列说法不一定正确的是( )
A.AC=DF B.BO=EO C.AD⊥l D.AB∥EF
8.如图,△ABC与△A′B′C′关于直线l对称,若∠A=50°,∠C=20°,则∠B'度数为( )
A.110° B.70° C.90° D.30°
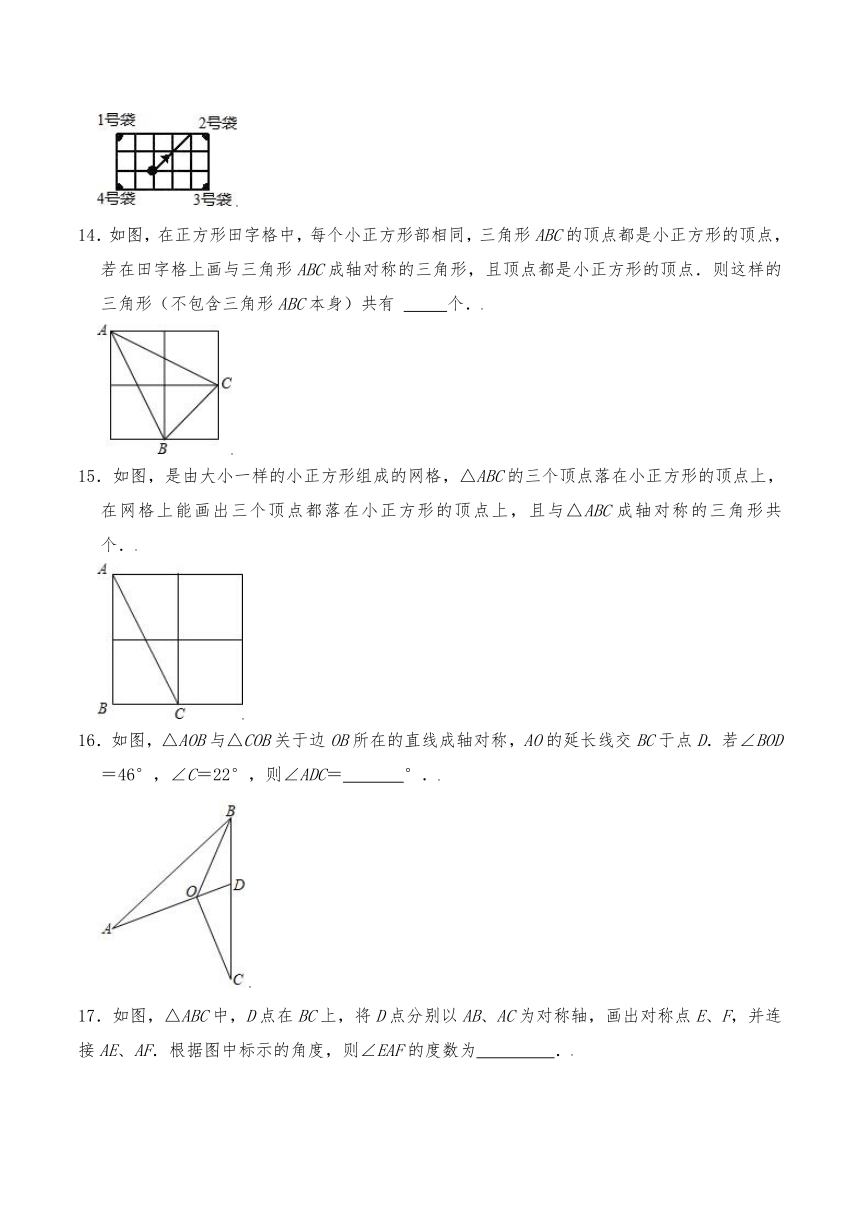
9.如图所示,l是四边形ABCD的对称轴,AD∥BC,现给出下列结论:
①AB∥CD;②AB=BC;③AB⊥BC;④AO=OC.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
10.如图,点P为∠AOB内一点,分别作出P点关于OB、OA的对称点P1,P2,连接P1P2交OB于M,交OA于N,若∠AOB=40°,则∠MPN的度数是( )
A.90° B.100° C.120° D.140°
二、填空题
11.下列图案是轴对称图形的有 个.
12.下列图形中,是轴对称图形的是 ,对称轴最多的图形是 ,有 条对称轴.
13.如图,一个经过改造的台球桌面上四个角的阴影部分分别表示四个入球孔,如果一个球按图中所示的方向被击出(球可以经过多次反射),那么该球最后将落入 号球袋.
14.如图,在正方形田字格中,每个小正方形部相同,三角形ABC的顶点都是小正方形的顶点,若在田字格上画与三角形ABC成轴对称的三角形,且顶点都是小正方形的顶点.则这样的三角形(不包含三角形ABC本身)共有 个.
15.如图,是由大小一样的小正方形组成的网格,△ABC的三个顶点落在小正方形的顶点上,在网格上能画出三个顶点都落在小正方形的顶点上,且与△ABC成轴对称的三角形共 个.
16.如图,△AOB与△COB关于边OB所在的直线成轴对称,AO的延长线交BC于点D.若∠BOD=46°,∠C=22°,则∠ADC= °.
17.如图,△ABC中,D点在BC上,将D点分别以AB、AC为对称轴,画出对称点E、F,并连接AE、AF.根据图中标示的角度,则∠EAF的度数为 .
18.如图,点P是∠AOB外一点,点M、N分别是∠AOB两边上的点,点P关于OA的对称点Q恰好落在线段MN上,点P关于OB的对称点R落在线段MN的延长线上.若PM=2.5cm,PN=3cm,MN=4cm,则线段QR的长为 .
三、解答题
19.在下列各图中分别补一个小正方形,使其成为不同的轴对称图形.
20.如图,将△ABC沿着DE折叠,使点A与点N重合,若∠A=65°,求∠1+∠2的度数.
21.如图,已知△ABC和△A'B'C'关于直线l成轴对称.
(1)在图中标出点A,B,C的对称点A',B',C';
(2)若AB=5,则对应线段A'B'= ;
(3)若∠A=50°,∠C'=20°,求∠B的度数.
22.如图,在△ABC中,直线l交AB于点M,交BC于点N,点B关于直线l的对称点D在线段BC上,且AD⊥MD,∠B=28°,求∠DAB的度数.
23.如图,点P在∠AOB的内部,点C和点P关于OA对称,点P关于OB对称点是D,连接CD交OA于M,交OB于N.
(1)①若∠AOB=60°,则∠COD= °;
②若∠AOB=α,求∠COD的度数.
(2)若CD=4,则△PMN的周长为 .
24.在△ABC中,∠BAC=90°,点D是BC上一点,将△ABD沿AD翻折后得到△AED,边AE交BC于点F.
(1)如图,当AE⊥BC时,写出图中所有与∠B相等的角: ;所有与∠C相等的角: .
(2)若∠C﹣∠B=50°,∠BAD=x°(0<x≤45).
①求∠B的度数;
②是否存在这样的x的值,使得△DEF中有两个角相等.若存在,并求x的值;若不存在,请说明理由.
答案
一、选择题
A.D.C.A.B.B.D.A.C.B.
二、填空题
11.2.
12.A、B、C;C,五.
13.1.
14.3.
15.5个.
16.70.
17.134°.
18.4.5cm.
三、解答题
19.如图所示:
20.∵△NDE是△ADE翻折变换而成,
∴∠AED=∠NED,∠ADE=∠NDE,∠A=∠N=65°,
∴∠AED+∠ADE=∠NED+∠NDE=180°﹣65°=115°,
∴∠1+∠2=360°﹣2×115°=130°.
21.(1)如图所示,A'、B'、C'、如图所示;
(2)A'B'=AB=5,
(3)∵△ABC与△A′B′C′关于直线l对称,
∴∠A=∠A′=50°,∠C=∠C′=20°;
∴∠B=180°﹣70°=110°.
故答案为:5;
22.∵点B关于直线l的对称点是点D,
∴直线l是线段DB的垂直平分线,
∴MD=MB,
∴∠MDB=∠B=28°,
∴∠AMD=∠MDB+∠B=56°,
在Rt△ADM中
∠DAB=90°﹣56°=34°.
23.(1)①∵点C和点P关于OA对称,
∴∠AOC=∠AOP,
∵点P关于OB对称点是D,
∴∠BOD=∠BOP,
∴∠COD=∠AOC+∠AOP+∠BOP+∠BOD=2(∠AOP+∠BOP)=2∠AOB=2×60°=120°,
故答案为:120°.
②∵点C和点P关于OA对称.
∴∠AOC=∠AOP,
∵点P关于OB对称点是D,
∴∠BOD=∠BOP,
∴∠COD=∠AOC+∠AOP+∠BOP+∠BOD=2(∠AOP+∠BOP)=2∠AOB=2α.
(2)根据轴对称的性质,可知CM=PM,DN=PN,
所以△PMN的周长为:PM+PN+MN=CM+DN+MN=CD=4,
故答案为:4
24.(1)∵∠BAC=90°,AE⊥BC,
∴∠CAF+∠BAF=90°,∠B+∠BAF=90°,
∴∠CAF=∠B,
由翻折可知,∠B=∠E,
∴∠B=∠CAF=∠E,
同理∠CAF+∠BAF=90°,∠C+∠CAF=90°,
∴∠C=∠BAF,
∵∠CAF=∠E,
∴AC∥DE,
∴∠C=∠CDE,
∴∠C=∠CDE=∠BAF.
故答案为:∠E、∠CAF;∠CDE、∠BAF;
(2)①∵∠C﹣∠B=50°,∠C+∠B=90°,
∴∠C=70°,∠B=20°;
②∠BAD=x°,则∠ADF=(20+x)°,
∴∠ADB=∠ADE=(160﹣x)°,
∴∠FDE=∠ADE﹣∠ADF=(140﹣2x)°,
∵∠B=∠E=20°,
∴∠DFE=180°﹣∠E﹣∠FDE=(2x+20)°,
当∠EDF=∠DFE时,140﹣2x=2x+20,
解得,x=30,
当∠DFE=∠E=20°时,2x+20=20,
解得,x=0,
∵0<x≤45,
∴不合题意,故舍去,
当∠EDF=∠E=20°,140﹣2x=20,
解得,x=60,
∵0<x≤45,
∴不合题意舍去.
综上可知,存在这样的x的值,使得△DEF中有两个角相等,且x=30.
一、选择题
1.2020年的春节,对于所有人来说真的不一般.为了打好疫情攻坚战,医护人员在岗位上同时间赛跑,与病魔较量,而我们每个人都能为打赢这场仗贡献一份力量.勤洗手,戴口罩,少聚会,积极配合;防控工作,照顾好自己和家人,还有,说出一句简单的:中国加油!武汉加油!在“中国加油”这4个美术字中,可以看作轴对称图形的是( )
A.中 B.国 C.加 D.油
2.下列古钱币图案中,轴对称图形的个数是( )
A.1 B.2 C.3 D.4
3.下列微信表情图标属于轴对称图形的是( )
A. B. C. D.
4.剪纸是我国传统的民间艺术.将一张纸片按图中①,②的方式沿虚线依次对折后,再沿图③中的虚线裁剪,最后将图④中的纸片打开铺平,所得图案应该是( )
A. B. C. D.
5.如图,△ABC与△A′B′C′关于直线l对称,且∠A=102°,∠C′=25°,则∠B的度数为( )
A.35° B.53° C.63° D.43°
6.如图,若△ABC与△A'B'C'关于直线MN对称,BB'交MN于点O,则下列说法中,不一定正确的是( )
A.AC=A'C' B.AB∥B'C' C.AA'⊥MN D.BO=B'O
7.如图,△ABC与△DEF关于直线l对称,BE交l于点O,则下列说法不一定正确的是( )
A.AC=DF B.BO=EO C.AD⊥l D.AB∥EF
8.如图,△ABC与△A′B′C′关于直线l对称,若∠A=50°,∠C=20°,则∠B'度数为( )
A.110° B.70° C.90° D.30°
9.如图所示,l是四边形ABCD的对称轴,AD∥BC,现给出下列结论:
①AB∥CD;②AB=BC;③AB⊥BC;④AO=OC.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
10.如图,点P为∠AOB内一点,分别作出P点关于OB、OA的对称点P1,P2,连接P1P2交OB于M,交OA于N,若∠AOB=40°,则∠MPN的度数是( )
A.90° B.100° C.120° D.140°
二、填空题
11.下列图案是轴对称图形的有 个.
12.下列图形中,是轴对称图形的是 ,对称轴最多的图形是 ,有 条对称轴.
13.如图,一个经过改造的台球桌面上四个角的阴影部分分别表示四个入球孔,如果一个球按图中所示的方向被击出(球可以经过多次反射),那么该球最后将落入 号球袋.
14.如图,在正方形田字格中,每个小正方形部相同,三角形ABC的顶点都是小正方形的顶点,若在田字格上画与三角形ABC成轴对称的三角形,且顶点都是小正方形的顶点.则这样的三角形(不包含三角形ABC本身)共有 个.
15.如图,是由大小一样的小正方形组成的网格,△ABC的三个顶点落在小正方形的顶点上,在网格上能画出三个顶点都落在小正方形的顶点上,且与△ABC成轴对称的三角形共 个.
16.如图,△AOB与△COB关于边OB所在的直线成轴对称,AO的延长线交BC于点D.若∠BOD=46°,∠C=22°,则∠ADC= °.
17.如图,△ABC中,D点在BC上,将D点分别以AB、AC为对称轴,画出对称点E、F,并连接AE、AF.根据图中标示的角度,则∠EAF的度数为 .
18.如图,点P是∠AOB外一点,点M、N分别是∠AOB两边上的点,点P关于OA的对称点Q恰好落在线段MN上,点P关于OB的对称点R落在线段MN的延长线上.若PM=2.5cm,PN=3cm,MN=4cm,则线段QR的长为 .
三、解答题
19.在下列各图中分别补一个小正方形,使其成为不同的轴对称图形.
20.如图,将△ABC沿着DE折叠,使点A与点N重合,若∠A=65°,求∠1+∠2的度数.
21.如图,已知△ABC和△A'B'C'关于直线l成轴对称.
(1)在图中标出点A,B,C的对称点A',B',C';
(2)若AB=5,则对应线段A'B'= ;
(3)若∠A=50°,∠C'=20°,求∠B的度数.
22.如图,在△ABC中,直线l交AB于点M,交BC于点N,点B关于直线l的对称点D在线段BC上,且AD⊥MD,∠B=28°,求∠DAB的度数.
23.如图,点P在∠AOB的内部,点C和点P关于OA对称,点P关于OB对称点是D,连接CD交OA于M,交OB于N.
(1)①若∠AOB=60°,则∠COD= °;
②若∠AOB=α,求∠COD的度数.
(2)若CD=4,则△PMN的周长为 .
24.在△ABC中,∠BAC=90°,点D是BC上一点,将△ABD沿AD翻折后得到△AED,边AE交BC于点F.
(1)如图,当AE⊥BC时,写出图中所有与∠B相等的角: ;所有与∠C相等的角: .
(2)若∠C﹣∠B=50°,∠BAD=x°(0<x≤45).
①求∠B的度数;
②是否存在这样的x的值,使得△DEF中有两个角相等.若存在,并求x的值;若不存在,请说明理由.
答案
一、选择题
A.D.C.A.B.B.D.A.C.B.
二、填空题
11.2.
12.A、B、C;C,五.
13.1.
14.3.
15.5个.
16.70.
17.134°.
18.4.5cm.
三、解答题
19.如图所示:
20.∵△NDE是△ADE翻折变换而成,
∴∠AED=∠NED,∠ADE=∠NDE,∠A=∠N=65°,
∴∠AED+∠ADE=∠NED+∠NDE=180°﹣65°=115°,
∴∠1+∠2=360°﹣2×115°=130°.
21.(1)如图所示,A'、B'、C'、如图所示;
(2)A'B'=AB=5,
(3)∵△ABC与△A′B′C′关于直线l对称,
∴∠A=∠A′=50°,∠C=∠C′=20°;
∴∠B=180°﹣70°=110°.
故答案为:5;
22.∵点B关于直线l的对称点是点D,
∴直线l是线段DB的垂直平分线,
∴MD=MB,
∴∠MDB=∠B=28°,
∴∠AMD=∠MDB+∠B=56°,
在Rt△ADM中
∠DAB=90°﹣56°=34°.
23.(1)①∵点C和点P关于OA对称,
∴∠AOC=∠AOP,
∵点P关于OB对称点是D,
∴∠BOD=∠BOP,
∴∠COD=∠AOC+∠AOP+∠BOP+∠BOD=2(∠AOP+∠BOP)=2∠AOB=2×60°=120°,
故答案为:120°.
②∵点C和点P关于OA对称.
∴∠AOC=∠AOP,
∵点P关于OB对称点是D,
∴∠BOD=∠BOP,
∴∠COD=∠AOC+∠AOP+∠BOP+∠BOD=2(∠AOP+∠BOP)=2∠AOB=2α.
(2)根据轴对称的性质,可知CM=PM,DN=PN,
所以△PMN的周长为:PM+PN+MN=CM+DN+MN=CD=4,
故答案为:4
24.(1)∵∠BAC=90°,AE⊥BC,
∴∠CAF+∠BAF=90°,∠B+∠BAF=90°,
∴∠CAF=∠B,
由翻折可知,∠B=∠E,
∴∠B=∠CAF=∠E,
同理∠CAF+∠BAF=90°,∠C+∠CAF=90°,
∴∠C=∠BAF,
∵∠CAF=∠E,
∴AC∥DE,
∴∠C=∠CDE,
∴∠C=∠CDE=∠BAF.
故答案为:∠E、∠CAF;∠CDE、∠BAF;
(2)①∵∠C﹣∠B=50°,∠C+∠B=90°,
∴∠C=70°,∠B=20°;
②∠BAD=x°,则∠ADF=(20+x)°,
∴∠ADB=∠ADE=(160﹣x)°,
∴∠FDE=∠ADE﹣∠ADF=(140﹣2x)°,
∵∠B=∠E=20°,
∴∠DFE=180°﹣∠E﹣∠FDE=(2x+20)°,
当∠EDF=∠DFE时,140﹣2x=2x+20,
解得,x=30,
当∠DFE=∠E=20°时,2x+20=20,
解得,x=0,
∵0<x≤45,
∴不合题意,故舍去,
当∠EDF=∠E=20°,140﹣2x=20,
解得,x=60,
∵0<x≤45,
∴不合题意舍去.
综上可知,存在这样的x的值,使得△DEF中有两个角相等,且x=30.
