沪科版八年级数学上册 15.2线段的垂直平分线 一课一练(含答案)
文档属性
| 名称 | 沪科版八年级数学上册 15.2线段的垂直平分线 一课一练(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 139.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-16 17:02:14 | ||
图片预览

文档简介
15.2线段的垂直平分线
一、选择题
1.如图,若记北京为A地,莫斯科为B地,雅典为C地,若想建立一个货物中转仓,使其到A、B、C三地的距离相等,则中转仓的位置应选在( )
A.三边垂直平分线的交点 B.三边中线的交点
C.三条角平分线的交点 D.三边上高的交点
2.如图,在△ABC中,∠BAC>90°,AB的垂直平分线交BC于点E,AC的垂直平分线交BC于点F,连接AE、AF,若△AEF的周长为2,则BC的长是( )
A.2 B.3 C.4 D.无法确定
3.如图:DE是△ABC中AC边的垂直平分线,若BC=8厘米,AB=10厘米,则△EBC的周长为( )厘米.
A.16 B.18 C.26 D.28
4.如图,在△ABC中,AC=4,BC边上的垂直平分线DE分别交BC、AB于点D,若△AEC的周长是11,则AB=( )
A.28 B.18 C.10 D.7
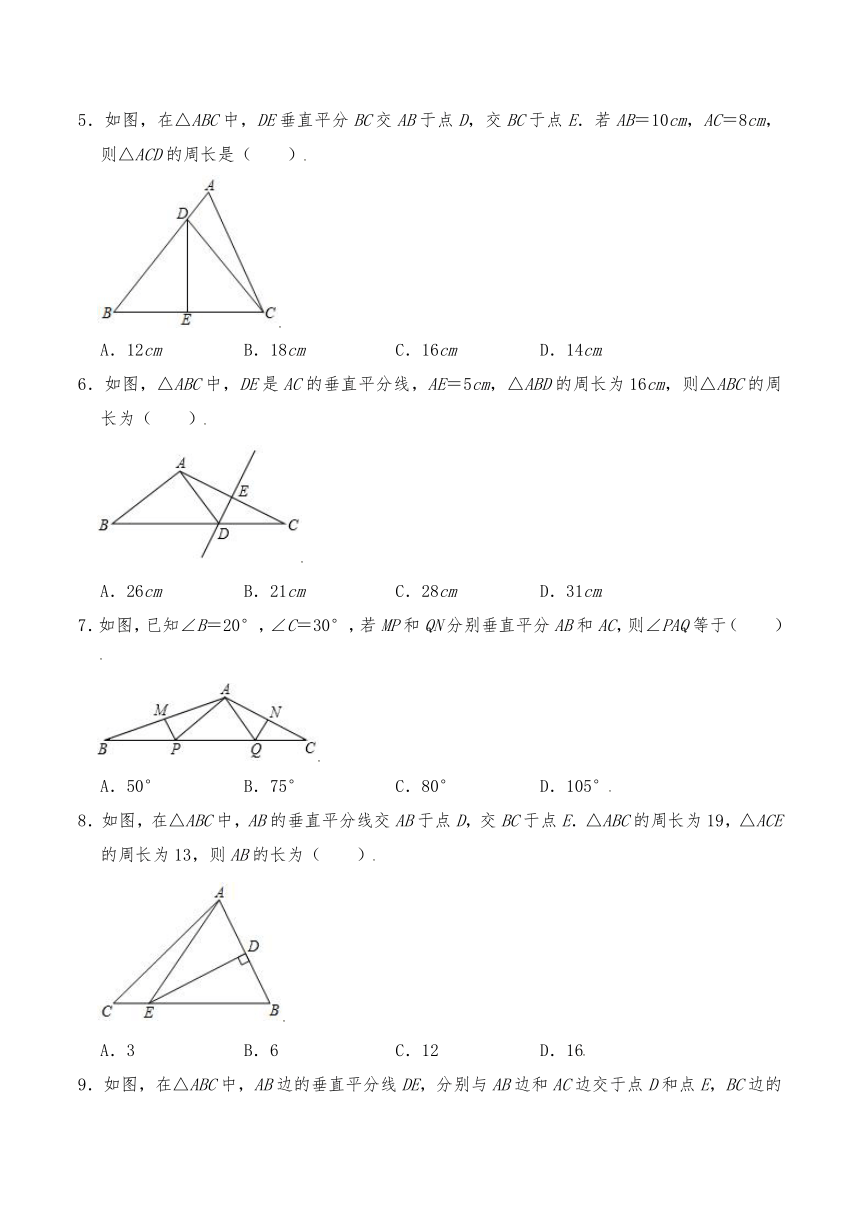
5.如图,在△ABC中,DE垂直平分BC交AB于点D,交BC于点E.若AB=10cm,AC=8cm,则△ACD的周长是( )
A.12cm B.18cm C.16cm D.14cm
6.如图,△ABC中,DE是AC的垂直平分线,AE=5cm,△ABD的周长为16cm,则△ABC的周长为( )
A.26cm B.21cm C.28cm D.31cm
7.如图,已知∠B=20°,∠C=30°,若MP和QN分别垂直平分AB和AC,则∠PAQ等于( )
A.50° B.75° C.80° D.105°
8.如图,在△ABC中,AB的垂直平分线交AB于点D,交BC于点E.△ABC的周长为19,△ACE的周长为13,则AB的长为( )
A.3 B.6 C.12 D.16
9.如图,在△ABC中,AB边的垂直平分线DE,分别与AB边和AC边交于点D和点E,BC边的垂直平分线FG,分别与BC边和AC边交于点F和点G,又△BEG的周长为16,且GE=1,则AC的长为( )
A.16 B.15 C.14 D.13
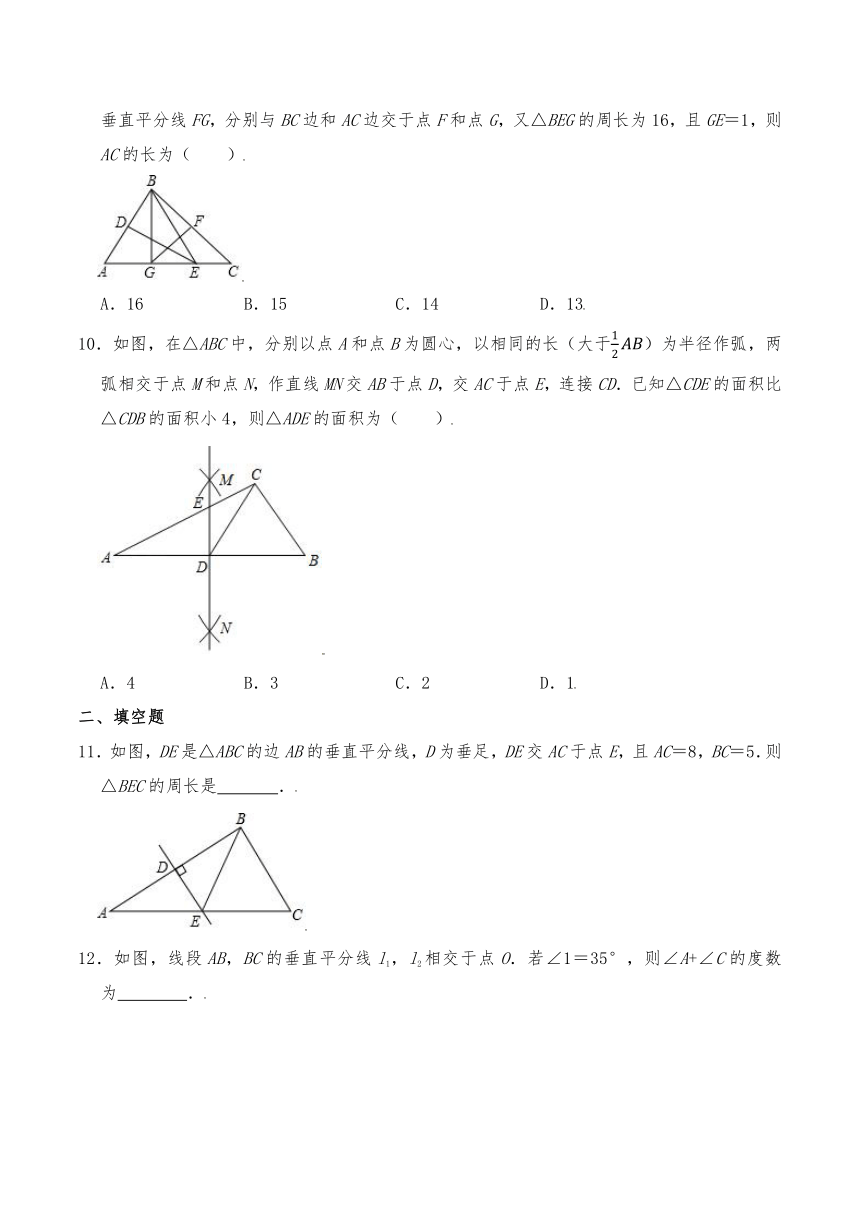
10.如图,在△ABC中,分别以点A和点B为圆心,以相同的长(大于)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交AC于点E,连接CD.已知△CDE的面积比△CDB的面积小4,则△ADE的面积为( )
A.4 B.3 C.2 D.1
二、填空题
11.如图,DE是△ABC的边AB的垂直平分线,D为垂足,DE交AC于点E,且AC=8,BC=5.则△BEC的周长是 .
12.如图,线段AB,BC的垂直平分线l1,l2相交于点O.若∠1=35°,则∠A+∠C的度数为 .
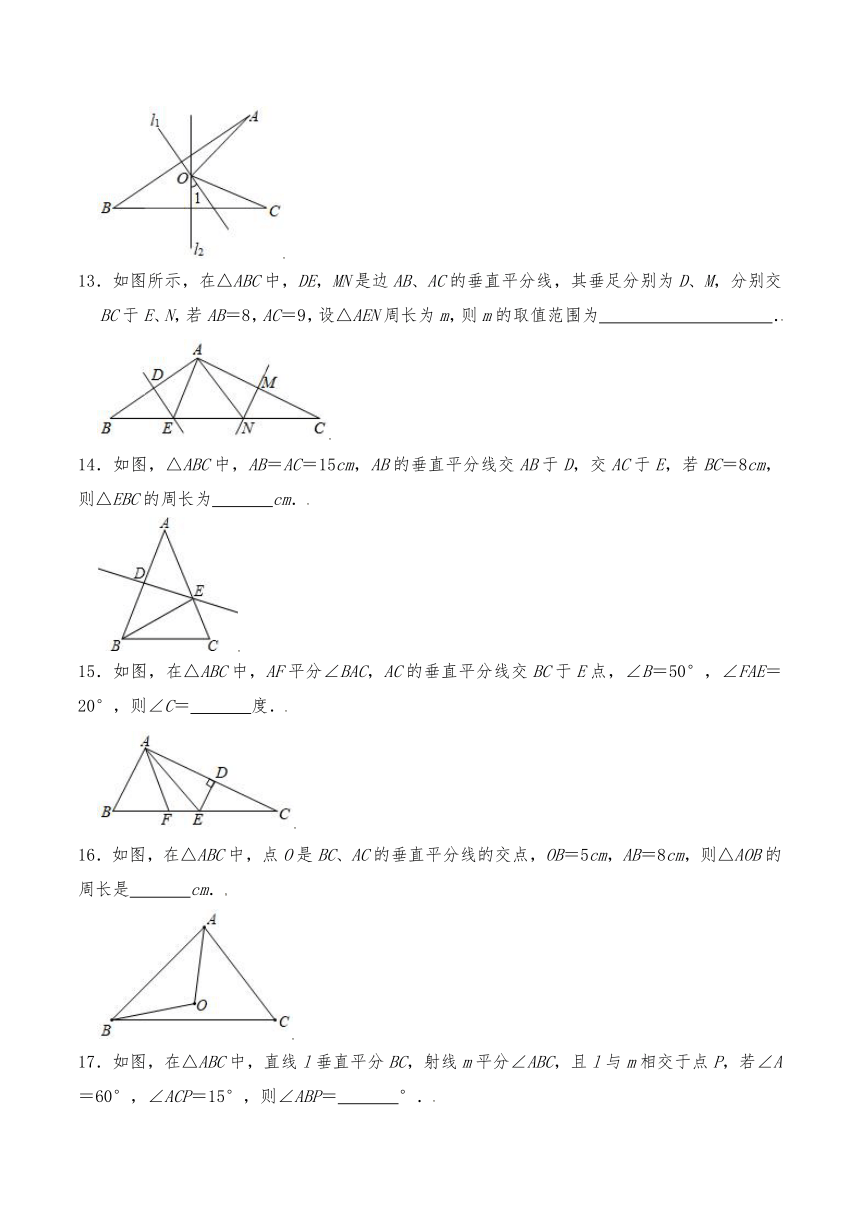
13.如图所示,在△ABC中,DE,MN是边AB、AC的垂直平分线,其垂足分别为D、M,分别交BC于E、N,若AB=8,AC=9,设△AEN周长为m,则m的取值范围为 .
14.如图,△ABC中,AB=AC=15cm,AB的垂直平分线交AB于D,交AC于E,若BC=8cm,则△EBC的周长为 cm.
15.如图,在△ABC中,AF平分∠BAC,AC的垂直平分线交BC于E点,∠B=50°,∠FAE=20°,则∠C= 度.
16.如图,在△ABC中,点O是BC、AC的垂直平分线的交点,OB=5cm,AB=8cm,则△AOB的周长是 cm.
17.如图,在△ABC中,直线l垂直平分BC,射线m平分∠ABC,且l与m相交于点P,若∠A=60°,∠ACP=15°,则∠ABP= °.
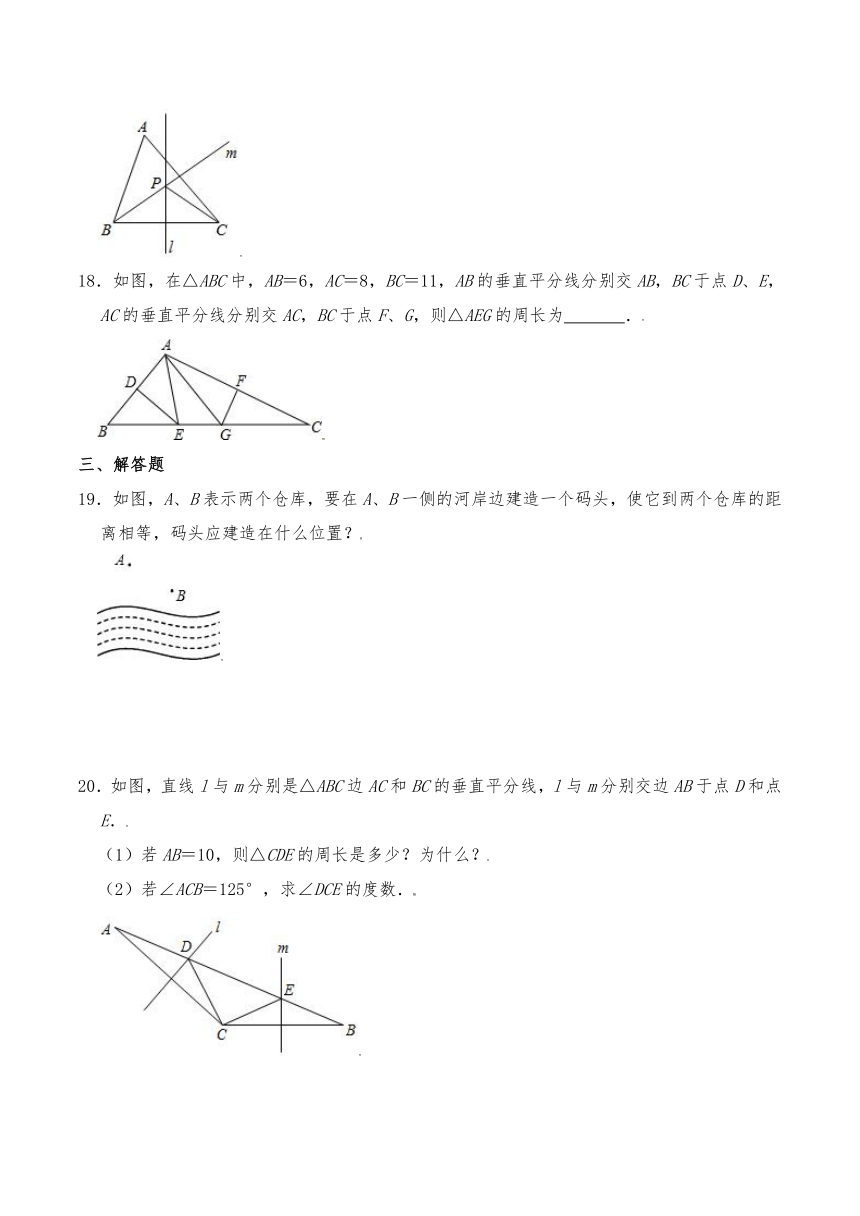
18.如图,在△ABC中,AB=6,AC=8,BC=11,AB的垂直平分线分别交AB,BC于点D、E,AC的垂直平分线分别交AC,BC于点F、G,则△AEG的周长为 .
三、解答题
19.如图,A、B表示两个仓库,要在A、B一侧的河岸边建造一个码头,使它到两个仓库的距离相等,码头应建造在什么位置?
20.如图,直线l与m分别是△ABC边AC和BC的垂直平分线,l与m分别交边AB于点D和点E.
(1)若AB=10,则△CDE的周长是多少?为什么?
(2)若∠ACB=125°,求∠DCE的度数.
21.如图,在△ABC中,∠C=90°,边AB的垂直平分线交AB,AC边分别为点D,点E,连接BE.
(1)若∠A=35°,求∠CBE的度数;
(2)若AB=10,BC=6,求△BCE的周长.
22.如图,在四边形ABCD中,BD所在的直线垂直平分线段AC,过点A作BC的平行线AF交CD于F,延长AB、DC交于点E.
求证:(1)AC平分∠EAF;
(2)∠FAD=∠E.
23.如图,在四边形ABCD中,点E是BC的中点,点F是CD的中点,且AE⊥BC,AF⊥CD.
(1)求证:AB=AD;
(2)请你探究∠EAF,∠BAE,∠DAF之间有什么数量关系?并证明你的结论.
24.如图,四边形ABCD中,∠A=∠B=90°,AB=25cm,DA=15cm,CB=10cm.动点
E从A点出发,以2cm/s的速度向B点移动,设移动的时间为x秒.
(1)当x为何值时,点E在线段CD的垂直平分线上?
(2)在(1)的条件下,判断DE与CE的位置关系,并说明理由.
答案
一、选择题
A.A.B.D.B.A.C.B.C.A.
二、填空题
11.13.
12.35°.
13.m<17.
14.23.
15.30.
16.18.
17.35.
18.11.
三、解答题
19.连接AB,码头应建在线段AB的垂直平分线与靠近A、B一侧的河岸的交汇点处.
如图:点P就是码头应建的位置.
20.(1)△CDE的周长为10.
∵直线l与m分别是△ABC边AC和BC的垂直平分线,
∴AD=CD,BE=CE,
∴△CDE的周长=CD+DE+CE=AD+DE+BE=AB=10;
(2)∵直线l与m分别是△ABC边AC和BC的垂直平分线,
∴AD=CD,BE=CE,
∴∠A=∠ACD,∠B=∠BCE,
又∵∠ACB=125°,
∴∠A+∠B=180°﹣125°=55°,
∴∠ACD+∠BCE=55°,
∴∠DCE=∠ACB﹣(∠ACD+∠BCE)=125°﹣55°=70°.
21.(1)∵∠C=90°,∠A=35°,
∴∠ABC=55°,
∵DE是边AB的垂直平分线,
∴EB=EA,
∴∠EBA=∠A=35°,
∴∠CBE=∠CBA﹣∠EBA=20°;
(2)∵AB=10,BC=6,
由勾股定理得,AC8,
∴△BCE的周长=BC+CE+EB=BC+CE+EA=BC+AC=14.
22.证明:(1)∵BD所在的直线垂直平分线段AC,
∴BA=BC,
∴∠BAC=∠BCA,
∵BC∥AF,
∴∠CAF=∠BCA,
∴∠CAF=∠BAC,即AC平分∠EAF;
(2)∵BD所在的直线垂直平分线段AC,
∴DA=DC,
∴∠DAC=∠DCA,
∵∠DCA是△ACE的一个外角,
∴∠DCA=∠E+∠EAC,
∴∠E+∠EAC=∠FAD+∠CAF,
∵∠CAF=∠EAC,
∴∠FAD=∠E.
23.(1)证明:连接AC,
∵点E是BC的中点,AE⊥BC,
∴AB=AC,
∵点F是CD的中点,AF⊥CD,
∴AD=AC,
∴AB=AD.
(2)∴∠EAF=∠BAE+∠DAF.
证明∵由(1)知AB=AC,
即△ABC为等腰三角形.
∵AE⊥BC,(已知),
∴∠BAE=∠EAC(等腰三角形的三线合一).
同理,∠CAF=∠DAF.
∴∠EAF=∠EAC+∠FAC=∠BAE+∠DAF.
24.(1)设AE=acm,则BE=(25﹣a)cm,
∵点E在线段CD的垂直平分线上,
∴DE=CE,
由勾股定理得:AD2+AE2=DE2,BC2+BE2=CE2,
∴AD2+AE2=BC2+BE2,
即152+a2=102+(25﹣a)2,
解得:a=10,
即AE=10(cm),
∴x5,
即当x=5时,点E在线段CD的垂直平分线上;
(2)DE与CE的位置关系是DE⊥CE,
理由是:∵△ADE≌△BEC,
∴∠ADE=∠CEB,
∵∠A=90°,
∴∠ADE+∠AED=90°,
∴∠AED+∠CEB=90°,
∴∠DEC=180°﹣(∠AED+∠CEB)=90°,
∴DE⊥CE.
一、选择题
1.如图,若记北京为A地,莫斯科为B地,雅典为C地,若想建立一个货物中转仓,使其到A、B、C三地的距离相等,则中转仓的位置应选在( )
A.三边垂直平分线的交点 B.三边中线的交点
C.三条角平分线的交点 D.三边上高的交点
2.如图,在△ABC中,∠BAC>90°,AB的垂直平分线交BC于点E,AC的垂直平分线交BC于点F,连接AE、AF,若△AEF的周长为2,则BC的长是( )
A.2 B.3 C.4 D.无法确定
3.如图:DE是△ABC中AC边的垂直平分线,若BC=8厘米,AB=10厘米,则△EBC的周长为( )厘米.
A.16 B.18 C.26 D.28
4.如图,在△ABC中,AC=4,BC边上的垂直平分线DE分别交BC、AB于点D,若△AEC的周长是11,则AB=( )
A.28 B.18 C.10 D.7
5.如图,在△ABC中,DE垂直平分BC交AB于点D,交BC于点E.若AB=10cm,AC=8cm,则△ACD的周长是( )
A.12cm B.18cm C.16cm D.14cm
6.如图,△ABC中,DE是AC的垂直平分线,AE=5cm,△ABD的周长为16cm,则△ABC的周长为( )
A.26cm B.21cm C.28cm D.31cm
7.如图,已知∠B=20°,∠C=30°,若MP和QN分别垂直平分AB和AC,则∠PAQ等于( )
A.50° B.75° C.80° D.105°
8.如图,在△ABC中,AB的垂直平分线交AB于点D,交BC于点E.△ABC的周长为19,△ACE的周长为13,则AB的长为( )
A.3 B.6 C.12 D.16
9.如图,在△ABC中,AB边的垂直平分线DE,分别与AB边和AC边交于点D和点E,BC边的垂直平分线FG,分别与BC边和AC边交于点F和点G,又△BEG的周长为16,且GE=1,则AC的长为( )
A.16 B.15 C.14 D.13
10.如图,在△ABC中,分别以点A和点B为圆心,以相同的长(大于)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交AC于点E,连接CD.已知△CDE的面积比△CDB的面积小4,则△ADE的面积为( )
A.4 B.3 C.2 D.1
二、填空题
11.如图,DE是△ABC的边AB的垂直平分线,D为垂足,DE交AC于点E,且AC=8,BC=5.则△BEC的周长是 .
12.如图,线段AB,BC的垂直平分线l1,l2相交于点O.若∠1=35°,则∠A+∠C的度数为 .
13.如图所示,在△ABC中,DE,MN是边AB、AC的垂直平分线,其垂足分别为D、M,分别交BC于E、N,若AB=8,AC=9,设△AEN周长为m,则m的取值范围为 .
14.如图,△ABC中,AB=AC=15cm,AB的垂直平分线交AB于D,交AC于E,若BC=8cm,则△EBC的周长为 cm.
15.如图,在△ABC中,AF平分∠BAC,AC的垂直平分线交BC于E点,∠B=50°,∠FAE=20°,则∠C= 度.
16.如图,在△ABC中,点O是BC、AC的垂直平分线的交点,OB=5cm,AB=8cm,则△AOB的周长是 cm.
17.如图,在△ABC中,直线l垂直平分BC,射线m平分∠ABC,且l与m相交于点P,若∠A=60°,∠ACP=15°,则∠ABP= °.
18.如图,在△ABC中,AB=6,AC=8,BC=11,AB的垂直平分线分别交AB,BC于点D、E,AC的垂直平分线分别交AC,BC于点F、G,则△AEG的周长为 .
三、解答题
19.如图,A、B表示两个仓库,要在A、B一侧的河岸边建造一个码头,使它到两个仓库的距离相等,码头应建造在什么位置?
20.如图,直线l与m分别是△ABC边AC和BC的垂直平分线,l与m分别交边AB于点D和点E.
(1)若AB=10,则△CDE的周长是多少?为什么?
(2)若∠ACB=125°,求∠DCE的度数.
21.如图,在△ABC中,∠C=90°,边AB的垂直平分线交AB,AC边分别为点D,点E,连接BE.
(1)若∠A=35°,求∠CBE的度数;
(2)若AB=10,BC=6,求△BCE的周长.
22.如图,在四边形ABCD中,BD所在的直线垂直平分线段AC,过点A作BC的平行线AF交CD于F,延长AB、DC交于点E.
求证:(1)AC平分∠EAF;
(2)∠FAD=∠E.
23.如图,在四边形ABCD中,点E是BC的中点,点F是CD的中点,且AE⊥BC,AF⊥CD.
(1)求证:AB=AD;
(2)请你探究∠EAF,∠BAE,∠DAF之间有什么数量关系?并证明你的结论.
24.如图,四边形ABCD中,∠A=∠B=90°,AB=25cm,DA=15cm,CB=10cm.动点
E从A点出发,以2cm/s的速度向B点移动,设移动的时间为x秒.
(1)当x为何值时,点E在线段CD的垂直平分线上?
(2)在(1)的条件下,判断DE与CE的位置关系,并说明理由.
答案
一、选择题
A.A.B.D.B.A.C.B.C.A.
二、填空题
11.13.
12.35°.
13.m<17.
14.23.
15.30.
16.18.
17.35.
18.11.
三、解答题
19.连接AB,码头应建在线段AB的垂直平分线与靠近A、B一侧的河岸的交汇点处.
如图:点P就是码头应建的位置.
20.(1)△CDE的周长为10.
∵直线l与m分别是△ABC边AC和BC的垂直平分线,
∴AD=CD,BE=CE,
∴△CDE的周长=CD+DE+CE=AD+DE+BE=AB=10;
(2)∵直线l与m分别是△ABC边AC和BC的垂直平分线,
∴AD=CD,BE=CE,
∴∠A=∠ACD,∠B=∠BCE,
又∵∠ACB=125°,
∴∠A+∠B=180°﹣125°=55°,
∴∠ACD+∠BCE=55°,
∴∠DCE=∠ACB﹣(∠ACD+∠BCE)=125°﹣55°=70°.
21.(1)∵∠C=90°,∠A=35°,
∴∠ABC=55°,
∵DE是边AB的垂直平分线,
∴EB=EA,
∴∠EBA=∠A=35°,
∴∠CBE=∠CBA﹣∠EBA=20°;
(2)∵AB=10,BC=6,
由勾股定理得,AC8,
∴△BCE的周长=BC+CE+EB=BC+CE+EA=BC+AC=14.
22.证明:(1)∵BD所在的直线垂直平分线段AC,
∴BA=BC,
∴∠BAC=∠BCA,
∵BC∥AF,
∴∠CAF=∠BCA,
∴∠CAF=∠BAC,即AC平分∠EAF;
(2)∵BD所在的直线垂直平分线段AC,
∴DA=DC,
∴∠DAC=∠DCA,
∵∠DCA是△ACE的一个外角,
∴∠DCA=∠E+∠EAC,
∴∠E+∠EAC=∠FAD+∠CAF,
∵∠CAF=∠EAC,
∴∠FAD=∠E.
23.(1)证明:连接AC,
∵点E是BC的中点,AE⊥BC,
∴AB=AC,
∵点F是CD的中点,AF⊥CD,
∴AD=AC,
∴AB=AD.
(2)∴∠EAF=∠BAE+∠DAF.
证明∵由(1)知AB=AC,
即△ABC为等腰三角形.
∵AE⊥BC,(已知),
∴∠BAE=∠EAC(等腰三角形的三线合一).
同理,∠CAF=∠DAF.
∴∠EAF=∠EAC+∠FAC=∠BAE+∠DAF.
24.(1)设AE=acm,则BE=(25﹣a)cm,
∵点E在线段CD的垂直平分线上,
∴DE=CE,
由勾股定理得:AD2+AE2=DE2,BC2+BE2=CE2,
∴AD2+AE2=BC2+BE2,
即152+a2=102+(25﹣a)2,
解得:a=10,
即AE=10(cm),
∴x5,
即当x=5时,点E在线段CD的垂直平分线上;
(2)DE与CE的位置关系是DE⊥CE,
理由是:∵△ADE≌△BEC,
∴∠ADE=∠CEB,
∵∠A=90°,
∴∠ADE+∠AED=90°,
∴∠AED+∠CEB=90°,
∴∠DEC=180°﹣(∠AED+∠CEB)=90°,
∴DE⊥CE.
