《中学教材全解》2013-2014学年八年级数学(上)(河北教育版)期中检测题(含答案)
文档属性
| 名称 | 《中学教材全解》2013-2014学年八年级数学(上)(河北教育版)期中检测题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 131.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-11-09 18:14:16 | ||
图片预览


文档简介
期中检测题
(本检测题满分:120分,时间:100分钟)
一、选择题(每小题3分,共36分)
1.化简的结果为( )
A. B. C. D.
2.两码头相距千米,一船顺水航行需小时,逆水航行需小时,那么水流速度为( )
A. B. C. D.
3.若表示一个整数,则整数n可取值的个数是( )
4.分式方程的解为( )
A. B. C. D.
5.甲计划用若干天完成某项工作,在甲独立工作两天后,乙加入此项工作,且甲、乙两人工效相同,结果提前两天完成任务.设甲计划完成此项工作的天数是,则的值为( )
A.5 B.6 C.7 D.8
6.如图,点在上,,,则全等三角形有 ( )
A.1对 B.2对 C.3对 D.4对
7.如图,在△ABC和△DEC中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是( )
A.BC=EC,∠B=∠E B.BC=EC,AC=DC
C.BC=DC,∠A=∠D D.∠B=∠E,∠A=∠D
8.若解分式方程产生增根,则( )
A.1 B.0 C.-4 D.-5
9.有下列说法:
(1)开方开不尽的数是无理数;
(2)无理数是无限不循环小数;
(3)无理数包括正无理数、零、负无理数;
(4)无理数都可以用数轴上的点来表示.
其中正确的说法的个数是( )
A.1 B.2 C.3 D.4
10.的平方根是( )
A. B. C. D.
11.若a,b为实数,且满足|-2|+=0,则b-的值为( )
A.2 B.0 C.-2 D.以上都不对
12.下列说法错误的是( )
A.5是25的算术平方根 B.1是1的一个平方根
C.的平方根是-4 D.0的平方根与算术平方根都是0
二、填空题(每小题3分,共24分)
13.化简:=______________.
14. 化简的结果为____________.
15.已知,则=______.
16.张明与李强共同清点一批图书,已知张明清点完本图书所用的时间与李强清点完 本图书所用的时间相同,且李强平均每分钟比张明多清点本,则张明平均每分钟清点图书 本.
17. 比较大小: (填“>”“<”或“=”).
18. 已知为两个连续的整数,且,则ab= .
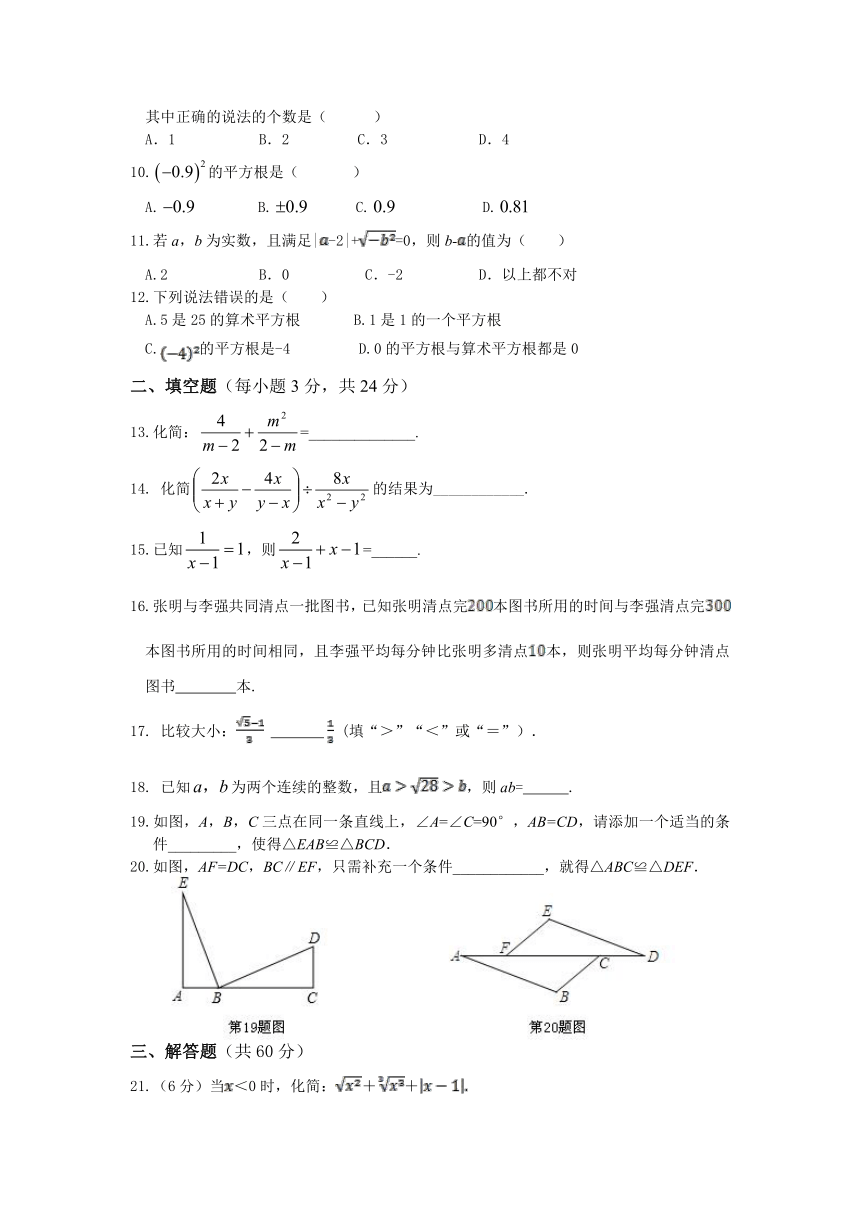
19.如图,A,B,C三点在同一条直线上,∠A=∠C=90°,AB=CD,请添加一个适当的条件_________,使得△EAB≌△BCD.
20.如图,AF=DC,BC∥EF,只需补充一个条件____________,就得△ABC≌△DEF.
三、解答题(共60分)
21.(6分)当<0时,化简:++
22.(6分)若, 求的值.
23.(6分)甲、乙两地相距,骑自行车从甲地到乙地,出发3小时20分钟后,骑摩托车也从甲地去乙地.已知的速度是的速度的3倍,结果两人同时到达乙地.求两人的速度.
24.(6分)已知求的值.
25.(6分)先化简,再求值:,其中
26.(8分)大家知道是无理数,而无理数是无限不循环小数,因此的小数部分我们不能全部地写出来,于是小平用-1来表示的小数部分,你同意小平的表示方法吗?
事实上小平的表示方法是有道理的,因为的整数部分是1,用这个数减去其整数部分,差就是小数部分.
请解答:已知:5+的小数部分是, 5-的整数部分是b,求+b的值.
27.(6分)如图,AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°,求∠3的度数.
28.(8分)如图,AB=AE,∠1=∠2,∠C=∠D.求证:△ABC≌△AED.
29.(8分)解答下列应用题:
⑴某房间的面积为17.6 m2,房间地面恰好由110块相同的正方形地砖铺成,每块地砖的边长是多少?
⑵已知第一个正方体水箱的棱长是60 cm,第二个正方体水箱的体积比第一个水箱的体积的3倍还多81 000 cm3,则第二个水箱需要铁皮多少平方米?
期中检测题参考答案
1.B 解析:
2.A 解析:因为两码头相距千米,一船顺水航行需小时,逆水航行需小时,
所以这艘船顺水航行的速度为,逆水航行的速度为.
所以水流的速度为
3.A 解析:若表示一个整数,则的取值可以是,所以整数的取值可以是,共6个.
4.C 解析:方程两边同乘,得,解得 .
经检验:是原方程的解.所以原方程的解是.
5.B 解析:由题意,得,解得.
6.C 解析:因为,,,所以△≌△,
所以.又因为,,所以△≌△.
所以.又因为,,所以△≌△.共有3对.
故选C.
7.C 解析:A.已知AB=DE,再加上条件BC=EC,∠B=∠E可利用SAS证明△ABC≌△DEC,故此选项不合题意;B.已知AB=DE,再加上条件BC=EC,AC=DC可利用SSS证明△ABC≌△DEC,故此选项不合题意;C.已知AB=DE,再加上条件BC=DC,∠A=∠D不能证明△ABC≌△DEC,故此选项符合题意;D.已知AB=DE,再加上条件∠B=∠E,∠A=∠D可利用ASA证明△ABC≌△DEC,故此选项不合题意;故选C.
8.D 解析:方程两边都乘,得又由题意知分式方程的增根为,把增根代入方程,得.
9.C 解析:本题考查对无理数的概念的理解.由于0是有理数,所以(3)应为无理数包括正无理数和负无理数.
10.B 解析:=0.81,0.81的平方根为
11.C 解析:∵ |-2|+=0,∴ =2,b=0,∴ b-=0-2=-2.故选C.
12.C 解析:A.因为=5,所以本说法正确;
B.因为±=±1,所以1是1的一个平方根,本说法正确;
C.因为±=±=±4,所以本说法错误;
D.因为=0, =0,所以本说法正确.
故选C.
13. 解析:
14. 解析:
15.3 解析:因为,所以,所以
16. 20 解析:设张明平均每分钟清点图书本,则李强平均每分钟清点图书(本,由题意列方程得,解得=20.经检验=20是原方程的解.
17. 解析:因为54,所以,所以所以即
18.30 解析:∵,,b为两个连续的整数, 又<<,∴ ∴ab=30.
19. AE=CB或EB=BD或∠EBD=90°或∠E=∠DBC等
解析:∵∠A=∠C=90°,AB=CD,∴若利用“SAS”,可添加AE=CB,
若利用“HL”,可添加EB=BD,
若利用“ASA”或“AAS”,可添加∠EBD=90°,
若添加∠E=∠DBC,可利用“AAS”证明.
综上所述,可添加的条件为AE=CB(或EB=BD或∠EBD=90°或∠E=∠DBC等).
20.BC=EF 解析:补充条件BC=EF,∵ AF=DC,∴ AF+FC=CD+FC,即AC=DF.
∵ BC∥EF,∴∠EFC=∠BCF,
在△ABC和△DEF中, ∵ EF=BC ,∠EFC=∠BCF, AC=DF ,
∴ △ABC≌△DEF(SAS).故答案为BC=EF.
21.解:++=.
因为所以原式=-
22.解:因为所以
所以
23.解:设的速度为千米/时,则的速度为千米/时.
根据题意,得方程
解这个方程,得.
经检验是原方程的根.
所以.
答:两人的速度分别为千米/时千米/时.
24.解:
把代入,得
25.解:
当时,
26. 解:∵ 4<5<9,∴ 2<<3,∴ 7<5+<8,∴ =-2.
又∵ -2>->-3,∴ 5-2>5->5-3,∴ 2<5-<3,∴ b=2,
∴ +b=-2+2=.
27.解:在△ABD与△ACE中,
∵ ∠1+∠CAD=∠CAE +∠CAD,∴ ∠1=∠CAE.
又∵ AB=AC,AD=AE,∴ △ABD ≌△ACE(SAS).∴ ∠2=∠ABD.
∵ ∠3=∠1+∠ABD=∠1+∠2,∠1=25°,∠2=30°,∴ ∠3=55°.
28.证明:∵∠1=∠2,∴∠1+∠EAC=∠2+∠EAC,即∠BAC=∠EAD.
在△ABC和△AED中,
∵ ∠D=∠C ,∠BAC=∠EAD, AB=AE,
∴ △ABC≌△AED(AAS).
29. 解:(1)每块地砖的面积为
所以正方形地砖的边长为
答:每块地砖的边长是0.4 m.
(2)由题意可知,第一个正方体水箱的体积为.
所以第二个正方体水箱的体积为
所以第二个正方体水箱的棱长为
所以需要铁皮.
(本检测题满分:120分,时间:100分钟)
一、选择题(每小题3分,共36分)
1.化简的结果为( )
A. B. C. D.
2.两码头相距千米,一船顺水航行需小时,逆水航行需小时,那么水流速度为( )
A. B. C. D.
3.若表示一个整数,则整数n可取值的个数是( )
4.分式方程的解为( )
A. B. C. D.
5.甲计划用若干天完成某项工作,在甲独立工作两天后,乙加入此项工作,且甲、乙两人工效相同,结果提前两天完成任务.设甲计划完成此项工作的天数是,则的值为( )
A.5 B.6 C.7 D.8
6.如图,点在上,,,则全等三角形有 ( )
A.1对 B.2对 C.3对 D.4对
7.如图,在△ABC和△DEC中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是( )
A.BC=EC,∠B=∠E B.BC=EC,AC=DC
C.BC=DC,∠A=∠D D.∠B=∠E,∠A=∠D
8.若解分式方程产生增根,则( )
A.1 B.0 C.-4 D.-5
9.有下列说法:
(1)开方开不尽的数是无理数;
(2)无理数是无限不循环小数;
(3)无理数包括正无理数、零、负无理数;
(4)无理数都可以用数轴上的点来表示.
其中正确的说法的个数是( )
A.1 B.2 C.3 D.4
10.的平方根是( )
A. B. C. D.
11.若a,b为实数,且满足|-2|+=0,则b-的值为( )
A.2 B.0 C.-2 D.以上都不对
12.下列说法错误的是( )
A.5是25的算术平方根 B.1是1的一个平方根
C.的平方根是-4 D.0的平方根与算术平方根都是0
二、填空题(每小题3分,共24分)
13.化简:=______________.
14. 化简的结果为____________.
15.已知,则=______.
16.张明与李强共同清点一批图书,已知张明清点完本图书所用的时间与李强清点完 本图书所用的时间相同,且李强平均每分钟比张明多清点本,则张明平均每分钟清点图书 本.
17. 比较大小: (填“>”“<”或“=”).
18. 已知为两个连续的整数,且,则ab= .
19.如图,A,B,C三点在同一条直线上,∠A=∠C=90°,AB=CD,请添加一个适当的条件_________,使得△EAB≌△BCD.
20.如图,AF=DC,BC∥EF,只需补充一个条件____________,就得△ABC≌△DEF.
三、解答题(共60分)
21.(6分)当<0时,化简:++
22.(6分)若, 求的值.
23.(6分)甲、乙两地相距,骑自行车从甲地到乙地,出发3小时20分钟后,骑摩托车也从甲地去乙地.已知的速度是的速度的3倍,结果两人同时到达乙地.求两人的速度.
24.(6分)已知求的值.
25.(6分)先化简,再求值:,其中
26.(8分)大家知道是无理数,而无理数是无限不循环小数,因此的小数部分我们不能全部地写出来,于是小平用-1来表示的小数部分,你同意小平的表示方法吗?
事实上小平的表示方法是有道理的,因为的整数部分是1,用这个数减去其整数部分,差就是小数部分.
请解答:已知:5+的小数部分是, 5-的整数部分是b,求+b的值.
27.(6分)如图,AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°,求∠3的度数.
28.(8分)如图,AB=AE,∠1=∠2,∠C=∠D.求证:△ABC≌△AED.
29.(8分)解答下列应用题:
⑴某房间的面积为17.6 m2,房间地面恰好由110块相同的正方形地砖铺成,每块地砖的边长是多少?
⑵已知第一个正方体水箱的棱长是60 cm,第二个正方体水箱的体积比第一个水箱的体积的3倍还多81 000 cm3,则第二个水箱需要铁皮多少平方米?
期中检测题参考答案
1.B 解析:
2.A 解析:因为两码头相距千米,一船顺水航行需小时,逆水航行需小时,
所以这艘船顺水航行的速度为,逆水航行的速度为.
所以水流的速度为
3.A 解析:若表示一个整数,则的取值可以是,所以整数的取值可以是,共6个.
4.C 解析:方程两边同乘,得,解得 .
经检验:是原方程的解.所以原方程的解是.
5.B 解析:由题意,得,解得.
6.C 解析:因为,,,所以△≌△,
所以.又因为,,所以△≌△.
所以.又因为,,所以△≌△.共有3对.
故选C.
7.C 解析:A.已知AB=DE,再加上条件BC=EC,∠B=∠E可利用SAS证明△ABC≌△DEC,故此选项不合题意;B.已知AB=DE,再加上条件BC=EC,AC=DC可利用SSS证明△ABC≌△DEC,故此选项不合题意;C.已知AB=DE,再加上条件BC=DC,∠A=∠D不能证明△ABC≌△DEC,故此选项符合题意;D.已知AB=DE,再加上条件∠B=∠E,∠A=∠D可利用ASA证明△ABC≌△DEC,故此选项不合题意;故选C.
8.D 解析:方程两边都乘,得又由题意知分式方程的增根为,把增根代入方程,得.
9.C 解析:本题考查对无理数的概念的理解.由于0是有理数,所以(3)应为无理数包括正无理数和负无理数.
10.B 解析:=0.81,0.81的平方根为
11.C 解析:∵ |-2|+=0,∴ =2,b=0,∴ b-=0-2=-2.故选C.
12.C 解析:A.因为=5,所以本说法正确;
B.因为±=±1,所以1是1的一个平方根,本说法正确;
C.因为±=±=±4,所以本说法错误;
D.因为=0, =0,所以本说法正确.
故选C.
13. 解析:
14. 解析:
15.3 解析:因为,所以,所以
16. 20 解析:设张明平均每分钟清点图书本,则李强平均每分钟清点图书(本,由题意列方程得,解得=20.经检验=20是原方程的解.
17. 解析:因为54,所以,所以所以即
18.30 解析:∵,,b为两个连续的整数, 又<<,∴ ∴ab=30.
19. AE=CB或EB=BD或∠EBD=90°或∠E=∠DBC等
解析:∵∠A=∠C=90°,AB=CD,∴若利用“SAS”,可添加AE=CB,
若利用“HL”,可添加EB=BD,
若利用“ASA”或“AAS”,可添加∠EBD=90°,
若添加∠E=∠DBC,可利用“AAS”证明.
综上所述,可添加的条件为AE=CB(或EB=BD或∠EBD=90°或∠E=∠DBC等).
20.BC=EF 解析:补充条件BC=EF,∵ AF=DC,∴ AF+FC=CD+FC,即AC=DF.
∵ BC∥EF,∴∠EFC=∠BCF,
在△ABC和△DEF中, ∵ EF=BC ,∠EFC=∠BCF, AC=DF ,
∴ △ABC≌△DEF(SAS).故答案为BC=EF.
21.解:++=.
因为所以原式=-
22.解:因为所以
所以
23.解:设的速度为千米/时,则的速度为千米/时.
根据题意,得方程
解这个方程,得.
经检验是原方程的根.
所以.
答:两人的速度分别为千米/时千米/时.
24.解:
把代入,得
25.解:
当时,
26. 解:∵ 4<5<9,∴ 2<<3,∴ 7<5+<8,∴ =-2.
又∵ -2>->-3,∴ 5-2>5->5-3,∴ 2<5-<3,∴ b=2,
∴ +b=-2+2=.
27.解:在△ABD与△ACE中,
∵ ∠1+∠CAD=∠CAE +∠CAD,∴ ∠1=∠CAE.
又∵ AB=AC,AD=AE,∴ △ABD ≌△ACE(SAS).∴ ∠2=∠ABD.
∵ ∠3=∠1+∠ABD=∠1+∠2,∠1=25°,∠2=30°,∴ ∠3=55°.
28.证明:∵∠1=∠2,∴∠1+∠EAC=∠2+∠EAC,即∠BAC=∠EAD.
在△ABC和△AED中,
∵ ∠D=∠C ,∠BAC=∠EAD, AB=AE,
∴ △ABC≌△AED(AAS).
29. 解:(1)每块地砖的面积为
所以正方形地砖的边长为
答:每块地砖的边长是0.4 m.
(2)由题意可知,第一个正方体水箱的体积为.
所以第二个正方体水箱的体积为
所以第二个正方体水箱的棱长为
所以需要铁皮.
同课章节目录
