【中学教材全解】2014届九年级数学(下)(青岛版)期中检测题(含答案)
文档属性
| 名称 | 【中学教材全解】2014届九年级数学(下)(青岛版)期中检测题(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 263.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-11-09 00:00:00 | ||
图片预览



文档简介
期中检测题
(本检测题满分:120分,时间:120分钟)
一、选择题(每小题3分,共36分)
1.已知一次函数的图象经过点,则该函数图象必经过点( )
A. B.
C. D.
2.下列函数中,随增大而减小的是( )
A. B.
C. D.
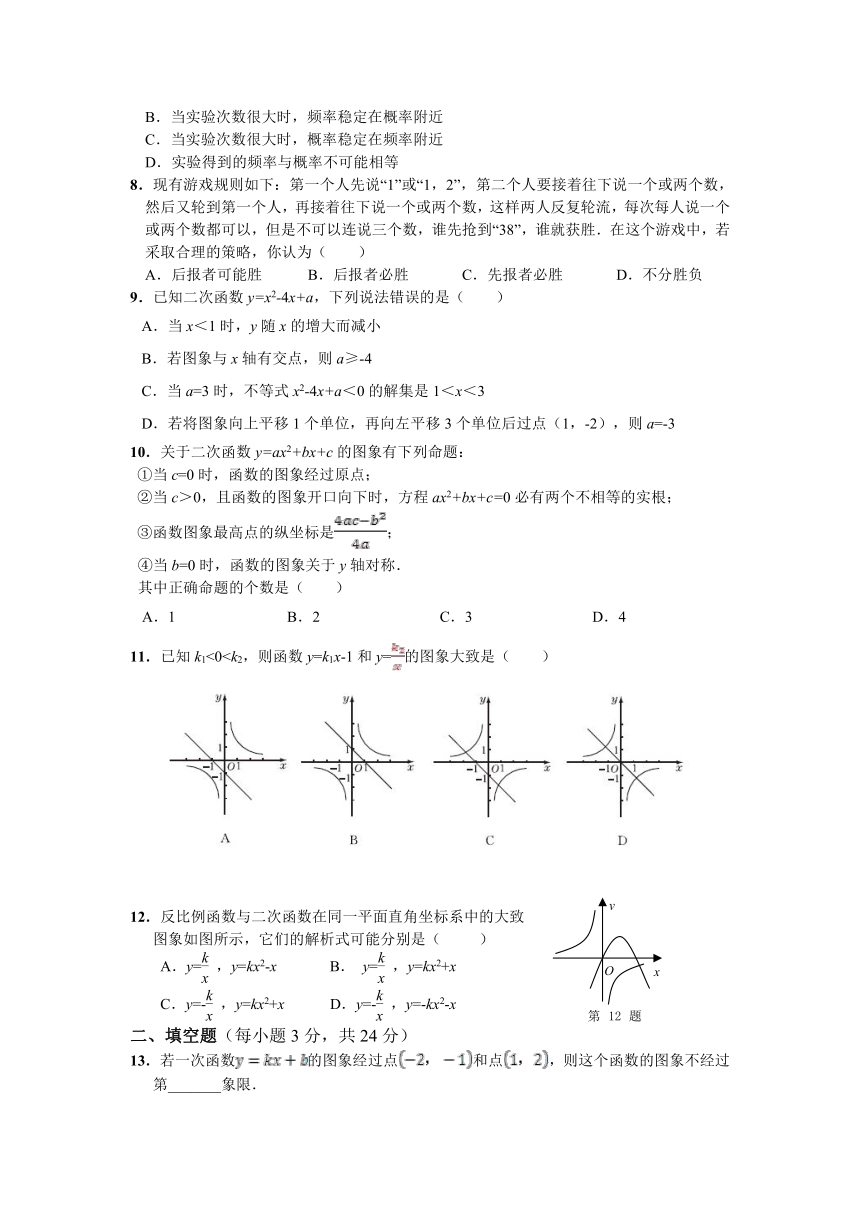
3. 甲、乙两辆摩托车同时分别从相距20 km的A,B两地出发,相向而行.图中l1,l2分别表示甲、乙两辆摩托车到A地的距离s(km)与行驶时间t(h)之间的函数关系.则下列说法错误的是( )
A.乙摩托车的速度较快
B.经过0.3 h甲摩托车行驶到A,B两地的中点
C.经过0.25 h两摩托车相遇
D.当乙摩托车到达A地时,甲摩托车距离A地km
4.已知正比例函数的图象上的两点,当时,有,那么的取值范围是( )
A. B.
C. D.
5.若一次函数的函数值随的增大而减小,且图象与轴的负半轴相交,那么对和的符号判断正确的是( )
A. B.
C. D.
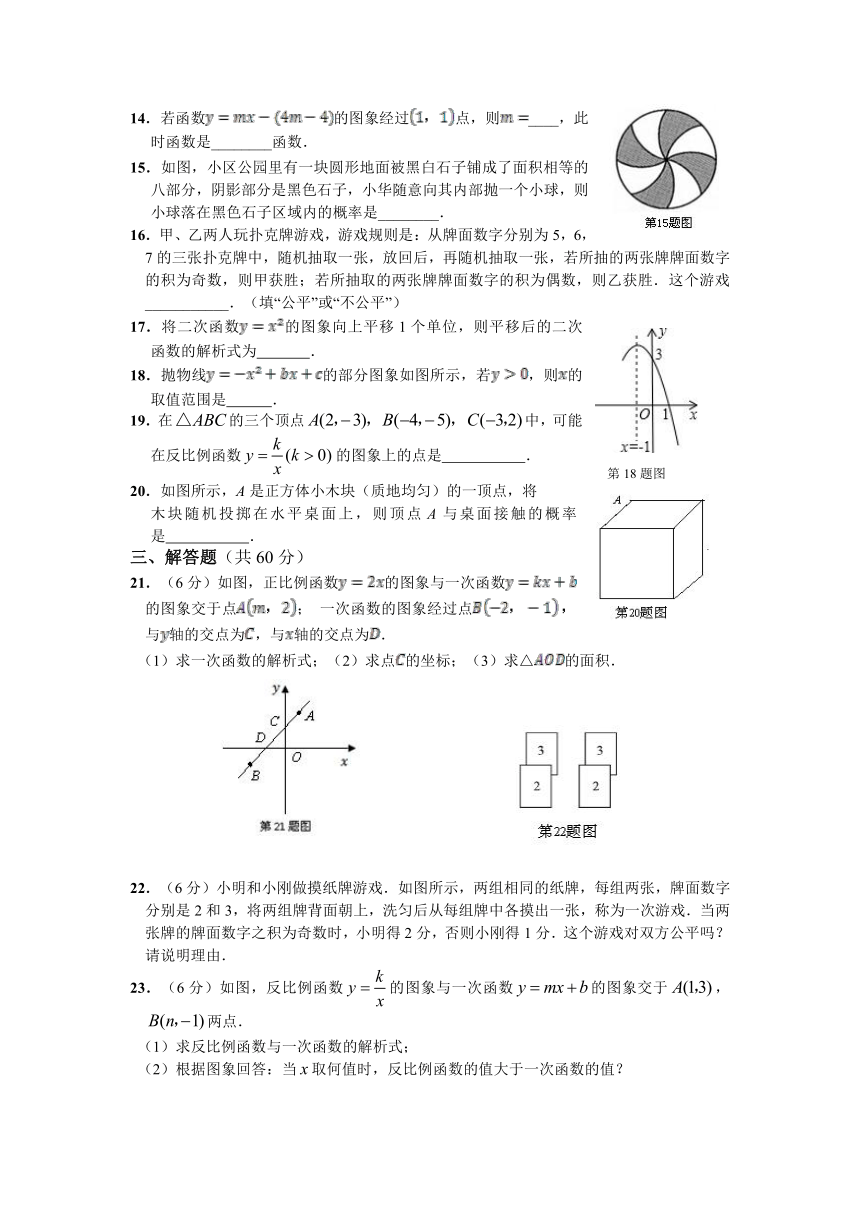
6. 一列快车从甲地驶往乙地,一列特快车从乙地驶往甲地,快车的速度为100千米/小时,特快车的速度为150千米/小时,甲、乙两地之间的距离为1 000千米,两车同时出发,则图中折线大致表示两车之间的距离y(千米)与快车行驶时间t(小时)之间的函数图象的是( )
7.关于频率和概率的关系,下列说法正确的是( )
A.频率等于概率
B.当实验次数很大时,频率稳定在概率附近
C.当实验次数很大时,概率稳定在频率附近
D.实验得到的频率与概率不可能相等
8.现有游戏规则如下:第一个人先说“1”或“1,2”,第二个人要接着往下说一个或两个数,然后又轮到第一个人,再接着往下说一个或两个数,这样两人反复轮流,每次每人说一个或两个数都可以,但是不可以连说三个数,谁先抢到“38”,谁就获胜.在这个游戏中,若采取合理的策略,你认为( )
A.后报者可能胜 B.后报者必胜 C.先报者必胜 D.不分胜负
9.已知二次函数y=x2-4x+a,下列说法错误的是( )
A.当x<1时,y随x的增大而减小
B.若图象与x轴有交点,则a≥-4
C.当a=3时,不等式x2-4x+a<0的解集是1<x<3
D.若将图象向上平移1个单位,再向左平移3个单位后过点(1,-2),则a=-3
10.关于二次函数y=ax2+bx+c的图象有下列命题:
①当c=0时,函数的图象经过原点;
②当c>0,且函数的图象开口向下时,方程ax2+bx+c=0必有两个不相等的实根;
③函数图象最高点的纵坐标是;
④当b=0时,函数的图象关于y轴对称.
其中正确命题的个数是( )
A.1 B.2 C.3 D.4
11.已知k1<012.反比例函数与二次函数在同一平面直角坐标系中的大致
图象如图所示,它们的解析式可能分别是( )
A.y=,y=kx2-x B. y=,y=kx2+x
C.y=-,y=kx2+x D.y=-,y=-kx2-x
二、填空题(每小题3分,共24分)
13.若一次函数的图象经过点和点,则这个函数的图象不经过第_______象限.
14.若函数的图象经过点,则____,此时函数是________函数.
15.如图,小区公园里有一块圆形地面被黑白石子铺成了面积相等的八部分,阴影部分是黑色石子,小华随意向其内部抛一个小球,则小球落在黑色石子区域内的概率是________.
16.甲、乙两人玩扑克牌游戏,游戏规则是:从牌面数字分别为5,6, 7的三张扑克牌中,随机抽取一张,放回后,再随机抽取一张,若所抽的两张牌牌面数字的积为奇数,则甲获胜;若所抽取的两张牌牌面数字的积为偶数,则乙获胜.这个游戏___________.(填“公平”或“不公平”)
17.将二次函数的图象向上平移1个单位,则平移后的二次 函数的解析式为 .
18.抛物线的部分图象如图所示,若,则的取值范围是 .
19.在的三个顶点中,可能在反比例函数的图象上的点是 .
20.如图所示,A是正方体小木块(质地均匀)的一顶点,将
木块随机投掷在水平桌面上,则顶点A与桌面接触的概率是 .
三、解答题(共60分)
21.(6分)如图,正比例函数的图象与一次函数的图象交于点; 一次函数的图象经过点与轴的交点为,与轴的交点为.
(1)求一次函数的解析式;(2)求点的坐标;(3)求△的面积.
22.(6分)小明和小刚做摸纸牌游戏.如图所示,两组相同的纸牌,每组两张,牌面数字分别是2和3,将两组牌背面朝上,洗匀后从每组牌中各摸出一张,称为一次游戏.当两张牌的牌面数字之积为奇数时,小明得2分,否则小刚得1分.这个游戏对双方公平吗?请说明理由.
23.(6分)如图,反比例函数的图象与一次函数的图象交于,两点.
(1)求反比例函数与一次函数的解析式;
(2)根据图象回答:当取何值时,反比例函数的值大于一次函数的值?
24.(6分)某公司市场营销部营销员的个人月收入与该营销员每月的销售量成一次函数关系,其图象如图所示.根据图象提供的信息,解答下列问题:
(1)求营销员个人月收入元与该营销员每月的销售量万件之间的函数解析式;
(2)已知该公司某营销员月份的销售量为1.2万件,求该营销员月份的收入.
25.(8分)某块实验田里的农作物每天的需水量y(千克)与生长时间x(天)之间的关系如图所示.这些农作物在第天、第天的需水量分别为千克、千克,在第天后每天的需水量比前一天增加千克.
(1)分别求出和时,与之间的函数解析式;
(2)如果这些农作物每天的需水量大于或等于千克时需要进行人工灌溉,那么应从第几天开始进行人工灌溉?
26.(8分)一只口袋中放着若干只红球和白球,这两种球除了颜色以外没有其他任何区别,袋中的球已经搅匀,蒙上眼睛从口袋中取出一只球,取到红球的概率是.
(1)取到白球的概率是多少?
(2)如果袋中的白球有18只,那么袋中的红球有多少只?
27.(10分)某公司有型产品件,型产品件,分配给下属甲、乙两个商店销售,其中件给甲店,件给乙店,且都能卖完.两商店销售这两种产品每件的利润(元)如下表:
型产品利润 型产品利润
甲店 200 170
乙店 160 150
(1)设分配给甲店型产品件,这家公司卖出这件产品的总利润为,求关于的函数解析式,并求出的取值范围;
(2)若公司要求总利润不低于元,说明有多少种不同分配方案,并将各种方案设计出来;
(3)为了促销,公司决定仅对甲店型产品让利销售,每件让利元,但让利后型产品的每件利润仍高于甲店型产品的每件利润,甲店的型产品以及乙店的型产品的每件利润不变,问该公司又如何设计分配方案,使总利润达到最大?
28.(10分)已知:如图,抛物线y=a(x-1)2+c与x轴交于点A(,0)和点B,将抛物线沿x轴向上翻折,顶点P落在点P'(1,3)处.
(1)求原抛物线的解析式;
(2)学校举行班徽设计比赛,九年级五班的小明在解答此题时顿生灵感:过点P'作x轴的平行线交抛物线于C,D两点,将翻折后得到的新图象在直线CD以上的部分去掉,设计成一个“W”型的班徽,“5”的拼音开头字母为W,“W”图案似大鹏展翅,寓意深远;而且小明通过计算惊奇地发现这个“W”图案的高与宽(CD)的比非常接近黄金分割比(约等于0.618).请你计算这个“W”图案的高与宽的比到底是多少?(参考数据:,,结果可保留根号)
第28题图
期中检测题参考答案
1.B 解析:由一次函数的图象经过点,知,所以,所以一次函数的解析式为,所以该一次函数必经过点.
2.D 解析:由一次函数的性质知,当时,函数值随自变量的增大而减小,故选D.
3. C 解析:观察函数的图象可以得出:甲摩托车的速度为20÷0.6=(km/h),乙摩托车的速度为20÷0.5=40(km/h),所以乙摩托车的速度较快,选项A正确;甲摩托车0.3 h走×0.3=10(km),所以经过0.3 h甲摩托车行驶到A,B两地的中点,选项B正确;经过0.25 h甲摩托车距A地×0.25=(km),乙摩托车距A地=10(km),所以两摩托车没有相遇,选项C不正确;乙摩托车到A地用了0.5 h,此时甲摩托车距A地×0.5=(km),选项D正确.
4.A 解析:由题意可知,故.
5.D 解析:由一次函数的函数值随的增大而减小,知;由它的图象与轴的负半轴相交,知.
6.C 解析:由题意知,此函数的图象应分为三段:当0≤t≤4时,两车之间的距离在逐渐缩小,两车经过4小时相遇,即当t=4时,两车之间的距离y=0;当两车相遇后再经过小时,特快车将到达甲地,即当47.B 解析:A.只能用频率估计概率;B正确;C.概率是定值;D.可以相等,如“抛硬币实验”,可得到正面向上的频率为,与概率相同.
8.C 解析:为了抢到,必须抢到35,那么不论另一个人报还是,你都能胜.游戏的关键是报数先后顺序,并且每次报数的个数和对方合起来是三个,即对方报个数,你就报个数.抢数游戏,它的本质是一个能否被“”整除的问题.谁先抢到35,对方无论报36还是36,37,你都获胜.
9.B 解析:二次函数为y=x2-4x+a,对称轴为直线x=2,图象开口向上,则:
A.当x<1时,y随x的增大而减小,故选项A正确;
B.若图象与x轴有交点,即Δ=16-4a≥0,则a≤4,故选项B错误;
C.当a=3时,不等式x2-4x+a<0的解集是1<x<3,故选项C正确;
D.原式化为y=(x-2)2-4+a,将图象向上平移1个单位,再向左平移3个单位后所得函数解析式是y=(x+1)2-3+a,又函数图象过点(1,-2),代入解析式得a=-3,故选项D正确.
10. C 解析:①c是二次函数y=ax2+bx+c的图象与y轴交点的纵坐标,所以当c=0时,函数的图象经过原点.
②c>0时,二次函数y=ax2+bx+c与y轴的交点在y轴的正半轴,又因为函数的图象开口向下,所以方程ax2+bx+c=0必有两个不相等的实根.
③当a<0时,函数图象最高点的纵坐标是;当a>0时,函数图象最低点的纵坐标是.由于a值不确定,故无法判断最高点或最低点.
④当b=0时,二次函数y=ax2+bx+c变为y=ax2+c,又因为y=ax2+c的图象与y=ax2的图象相同,所以当b=0时,函数的图象关于y轴对称.
命题①②④正确,故选C.
11.A 解析:由k2>0知,函数y=的图象分别位于第一、三象限;由k1<0知,函数y=k1x-1经过第二、三、四象限.故选A.
12.B 解析:当k>0时,由图象知首先排除A,B,再由二次函数图象的对称轴大于0知C,D也不正确;当k<0时,由图象知首先排除C,D,再由二次函数图象的对称轴大于0知A不正确,故选B.
13.四 解析:由题意,得解得所以这个函数的解析式为,所以这个函数的图象不经过第四象限.
14.1 正比例 解析:由函数的图象经过点,知,所以所以函数的解析式为此时函数为正比例函数.
15. 解析:圆形地面被分成面积相等的八部分,其中阴影占四部分,所以小球落在黑色石子区域内的概率是.
16. 不公平 解析:画树状图如图所示,可知甲获胜的概率是,乙获胜的概率是,两个概率值不相等,故这个游戏不公平.
17. 解析:熟记函数图象的平移规律:左加右减,上加下减.
18. -3<<1 解析:根据抛物线的图象可知:抛物线的对称轴为直线,已知一个交点为(1,0),根据轴对称性,则另一个交点为(-3,0),所以时,的取值范围是-3<<1.
19.B 解析:由于反比例函数中的系数,所以只要点的两个坐标的乘积大于0即可,因此点B可能在反比例函数的图象上.
20. 解析:将木块随机投掷在水平桌面上,正方体的六个面都可能与桌面接触,因为A是正方体小木块三个面的交点,所以当这三个面中的任一面与桌面接触时,顶点A都与桌面接触.所以P(顶点A与桌面接触)==.
21.解:(1)把点的坐标代入中,得,所以.
将点,的坐标分别代入中,
得解得所以这个函数的解析式为.
(2)当时,所以点的坐标为.
(3)在中,当时,,所以,
所以△的面积为
22. 分析:本题考查了概率的计算与实际应用,利用列表法或树状图法列出两张牌的牌面数字之积的所有等可能结果,利用概率计算公式可求两张牌的牌面数字之积为奇数的概率.
解:
第一张牌牌面上的数字积第二张牌牌面上的数字 2 3
2 4 6
3 6 9
∴ P(积为奇数)=,P(积为偶数)=.
∴ 小明得分:×2=(分),小刚得分:×1=(分).
∵ ≠ ,∴ 这个游戏对双方不公平.
点拨:判断游戏的公平性关键是计算每个事件的概率,如果概率相等就公平,否则就不公平.此类题型一般通过比较概率的大小求解.
概率计算公式为:P(A)=.
23. 解:(1)∵点在的图象上,∴,∴.
又∵点在的图象上,,即 .
由点,在的图象上,知解得
所以反比例函数的解析式为,一次函数的解析式为.
(2)从图象上可知,当或时,反比例函数的值大于一次函数的值.
24.解:(1)依题意,设.
因为函数图象过和两点,
所以,,
所以,所以.
(2)当时,,
即该营销员5月份的收入为元.
25.解:(1)当时,设.
根据题意,得解得
所以当时,与之间的函数解析式是.
所以当时,.
当时,根据题意,得,即.
所以当时,与之间的函数解析式是.
(2)当时,与之间的函数解析式是.
解,得,
所以应从第45天开始进行人工灌溉.
26.解:(1)
(2)设袋中的红球有只,则有 或,解得.
所以袋中的红球有6只.
27.解:(1)由题意,知甲店有型产品件,
乙店有型产品件,有型产品件,
则.
由得
(2)由
所以有三种不同的分配方案:
①时,甲店型38件,型32件,乙店型2件,型28件;
②时,甲店型39件,型31件,乙店型1件,型29件;
③时,甲店型40件,型30件,乙店型0件,型30件.
(3)依题意,有
.
①若,当时,即甲店型40件,型30件,乙店型0件,型30件,能使总利润达到最大;
②若,当时,即符合题意的各种方案,使总利润都相同;
③若,当时,即甲店型10件,型60件,乙店型30件,型0件,能使总利润达到最大.
28. 解:(1)∵ 点P与P′(1,3)关于x轴对称,
∴ 点P的坐标为(1,﹣3).
∵ 抛物线y=a(x﹣1)2+c过点A(,0),顶点是P(1,﹣3),
∴ 解得
则抛物线的解析式为y=(x﹣1)2﹣3,
即y=x2﹣2x﹣2.
(2)∵ CD平行x轴,点P′(1,3)在CD上,
∴ C,D两点的纵坐标为3.
由(x﹣1)2﹣3=3,解得,,
∴ C,D两点的坐标分别为(,3),(,3).
∴ CD=.
∴ “W”图案的高与宽(CD)的比=.
O
x
y
第12题图
第18题图
(本检测题满分:120分,时间:120分钟)
一、选择题(每小题3分,共36分)
1.已知一次函数的图象经过点,则该函数图象必经过点( )
A. B.
C. D.
2.下列函数中,随增大而减小的是( )
A. B.
C. D.
3. 甲、乙两辆摩托车同时分别从相距20 km的A,B两地出发,相向而行.图中l1,l2分别表示甲、乙两辆摩托车到A地的距离s(km)与行驶时间t(h)之间的函数关系.则下列说法错误的是( )
A.乙摩托车的速度较快
B.经过0.3 h甲摩托车行驶到A,B两地的中点
C.经过0.25 h两摩托车相遇
D.当乙摩托车到达A地时,甲摩托车距离A地km
4.已知正比例函数的图象上的两点,当时,有,那么的取值范围是( )
A. B.
C. D.
5.若一次函数的函数值随的增大而减小,且图象与轴的负半轴相交,那么对和的符号判断正确的是( )
A. B.
C. D.
6. 一列快车从甲地驶往乙地,一列特快车从乙地驶往甲地,快车的速度为100千米/小时,特快车的速度为150千米/小时,甲、乙两地之间的距离为1 000千米,两车同时出发,则图中折线大致表示两车之间的距离y(千米)与快车行驶时间t(小时)之间的函数图象的是( )
7.关于频率和概率的关系,下列说法正确的是( )
A.频率等于概率
B.当实验次数很大时,频率稳定在概率附近
C.当实验次数很大时,概率稳定在频率附近
D.实验得到的频率与概率不可能相等
8.现有游戏规则如下:第一个人先说“1”或“1,2”,第二个人要接着往下说一个或两个数,然后又轮到第一个人,再接着往下说一个或两个数,这样两人反复轮流,每次每人说一个或两个数都可以,但是不可以连说三个数,谁先抢到“38”,谁就获胜.在这个游戏中,若采取合理的策略,你认为( )
A.后报者可能胜 B.后报者必胜 C.先报者必胜 D.不分胜负
9.已知二次函数y=x2-4x+a,下列说法错误的是( )
A.当x<1时,y随x的增大而减小
B.若图象与x轴有交点,则a≥-4
C.当a=3时,不等式x2-4x+a<0的解集是1<x<3
D.若将图象向上平移1个单位,再向左平移3个单位后过点(1,-2),则a=-3
10.关于二次函数y=ax2+bx+c的图象有下列命题:
①当c=0时,函数的图象经过原点;
②当c>0,且函数的图象开口向下时,方程ax2+bx+c=0必有两个不相等的实根;
③函数图象最高点的纵坐标是;
④当b=0时,函数的图象关于y轴对称.
其中正确命题的个数是( )
A.1 B.2 C.3 D.4
11.已知k1<0
图象如图所示,它们的解析式可能分别是( )
A.y=,y=kx2-x B. y=,y=kx2+x
C.y=-,y=kx2+x D.y=-,y=-kx2-x
二、填空题(每小题3分,共24分)
13.若一次函数的图象经过点和点,则这个函数的图象不经过第_______象限.
14.若函数的图象经过点,则____,此时函数是________函数.
15.如图,小区公园里有一块圆形地面被黑白石子铺成了面积相等的八部分,阴影部分是黑色石子,小华随意向其内部抛一个小球,则小球落在黑色石子区域内的概率是________.
16.甲、乙两人玩扑克牌游戏,游戏规则是:从牌面数字分别为5,6, 7的三张扑克牌中,随机抽取一张,放回后,再随机抽取一张,若所抽的两张牌牌面数字的积为奇数,则甲获胜;若所抽取的两张牌牌面数字的积为偶数,则乙获胜.这个游戏___________.(填“公平”或“不公平”)
17.将二次函数的图象向上平移1个单位,则平移后的二次 函数的解析式为 .
18.抛物线的部分图象如图所示,若,则的取值范围是 .
19.在的三个顶点中,可能在反比例函数的图象上的点是 .
20.如图所示,A是正方体小木块(质地均匀)的一顶点,将
木块随机投掷在水平桌面上,则顶点A与桌面接触的概率是 .
三、解答题(共60分)
21.(6分)如图,正比例函数的图象与一次函数的图象交于点; 一次函数的图象经过点与轴的交点为,与轴的交点为.
(1)求一次函数的解析式;(2)求点的坐标;(3)求△的面积.
22.(6分)小明和小刚做摸纸牌游戏.如图所示,两组相同的纸牌,每组两张,牌面数字分别是2和3,将两组牌背面朝上,洗匀后从每组牌中各摸出一张,称为一次游戏.当两张牌的牌面数字之积为奇数时,小明得2分,否则小刚得1分.这个游戏对双方公平吗?请说明理由.
23.(6分)如图,反比例函数的图象与一次函数的图象交于,两点.
(1)求反比例函数与一次函数的解析式;
(2)根据图象回答:当取何值时,反比例函数的值大于一次函数的值?
24.(6分)某公司市场营销部营销员的个人月收入与该营销员每月的销售量成一次函数关系,其图象如图所示.根据图象提供的信息,解答下列问题:
(1)求营销员个人月收入元与该营销员每月的销售量万件之间的函数解析式;
(2)已知该公司某营销员月份的销售量为1.2万件,求该营销员月份的收入.
25.(8分)某块实验田里的农作物每天的需水量y(千克)与生长时间x(天)之间的关系如图所示.这些农作物在第天、第天的需水量分别为千克、千克,在第天后每天的需水量比前一天增加千克.
(1)分别求出和时,与之间的函数解析式;
(2)如果这些农作物每天的需水量大于或等于千克时需要进行人工灌溉,那么应从第几天开始进行人工灌溉?
26.(8分)一只口袋中放着若干只红球和白球,这两种球除了颜色以外没有其他任何区别,袋中的球已经搅匀,蒙上眼睛从口袋中取出一只球,取到红球的概率是.
(1)取到白球的概率是多少?
(2)如果袋中的白球有18只,那么袋中的红球有多少只?
27.(10分)某公司有型产品件,型产品件,分配给下属甲、乙两个商店销售,其中件给甲店,件给乙店,且都能卖完.两商店销售这两种产品每件的利润(元)如下表:
型产品利润 型产品利润
甲店 200 170
乙店 160 150
(1)设分配给甲店型产品件,这家公司卖出这件产品的总利润为,求关于的函数解析式,并求出的取值范围;
(2)若公司要求总利润不低于元,说明有多少种不同分配方案,并将各种方案设计出来;
(3)为了促销,公司决定仅对甲店型产品让利销售,每件让利元,但让利后型产品的每件利润仍高于甲店型产品的每件利润,甲店的型产品以及乙店的型产品的每件利润不变,问该公司又如何设计分配方案,使总利润达到最大?
28.(10分)已知:如图,抛物线y=a(x-1)2+c与x轴交于点A(,0)和点B,将抛物线沿x轴向上翻折,顶点P落在点P'(1,3)处.
(1)求原抛物线的解析式;
(2)学校举行班徽设计比赛,九年级五班的小明在解答此题时顿生灵感:过点P'作x轴的平行线交抛物线于C,D两点,将翻折后得到的新图象在直线CD以上的部分去掉,设计成一个“W”型的班徽,“5”的拼音开头字母为W,“W”图案似大鹏展翅,寓意深远;而且小明通过计算惊奇地发现这个“W”图案的高与宽(CD)的比非常接近黄金分割比(约等于0.618).请你计算这个“W”图案的高与宽的比到底是多少?(参考数据:,,结果可保留根号)
第28题图
期中检测题参考答案
1.B 解析:由一次函数的图象经过点,知,所以,所以一次函数的解析式为,所以该一次函数必经过点.
2.D 解析:由一次函数的性质知,当时,函数值随自变量的增大而减小,故选D.
3. C 解析:观察函数的图象可以得出:甲摩托车的速度为20÷0.6=(km/h),乙摩托车的速度为20÷0.5=40(km/h),所以乙摩托车的速度较快,选项A正确;甲摩托车0.3 h走×0.3=10(km),所以经过0.3 h甲摩托车行驶到A,B两地的中点,选项B正确;经过0.25 h甲摩托车距A地×0.25=(km),乙摩托车距A地=10(km),所以两摩托车没有相遇,选项C不正确;乙摩托车到A地用了0.5 h,此时甲摩托车距A地×0.5=(km),选项D正确.
4.A 解析:由题意可知,故.
5.D 解析:由一次函数的函数值随的增大而减小,知;由它的图象与轴的负半轴相交,知.
6.C 解析:由题意知,此函数的图象应分为三段:当0≤t≤4时,两车之间的距离在逐渐缩小,两车经过4小时相遇,即当t=4时,两车之间的距离y=0;当两车相遇后再经过小时,特快车将到达甲地,即当4
8.C 解析:为了抢到,必须抢到35,那么不论另一个人报还是,你都能胜.游戏的关键是报数先后顺序,并且每次报数的个数和对方合起来是三个,即对方报个数,你就报个数.抢数游戏,它的本质是一个能否被“”整除的问题.谁先抢到35,对方无论报36还是36,37,你都获胜.
9.B 解析:二次函数为y=x2-4x+a,对称轴为直线x=2,图象开口向上,则:
A.当x<1时,y随x的增大而减小,故选项A正确;
B.若图象与x轴有交点,即Δ=16-4a≥0,则a≤4,故选项B错误;
C.当a=3时,不等式x2-4x+a<0的解集是1<x<3,故选项C正确;
D.原式化为y=(x-2)2-4+a,将图象向上平移1个单位,再向左平移3个单位后所得函数解析式是y=(x+1)2-3+a,又函数图象过点(1,-2),代入解析式得a=-3,故选项D正确.
10. C 解析:①c是二次函数y=ax2+bx+c的图象与y轴交点的纵坐标,所以当c=0时,函数的图象经过原点.
②c>0时,二次函数y=ax2+bx+c与y轴的交点在y轴的正半轴,又因为函数的图象开口向下,所以方程ax2+bx+c=0必有两个不相等的实根.
③当a<0时,函数图象最高点的纵坐标是;当a>0时,函数图象最低点的纵坐标是.由于a值不确定,故无法判断最高点或最低点.
④当b=0时,二次函数y=ax2+bx+c变为y=ax2+c,又因为y=ax2+c的图象与y=ax2的图象相同,所以当b=0时,函数的图象关于y轴对称.
命题①②④正确,故选C.
11.A 解析:由k2>0知,函数y=的图象分别位于第一、三象限;由k1<0知,函数y=k1x-1经过第二、三、四象限.故选A.
12.B 解析:当k>0时,由图象知首先排除A,B,再由二次函数图象的对称轴大于0知C,D也不正确;当k<0时,由图象知首先排除C,D,再由二次函数图象的对称轴大于0知A不正确,故选B.
13.四 解析:由题意,得解得所以这个函数的解析式为,所以这个函数的图象不经过第四象限.
14.1 正比例 解析:由函数的图象经过点,知,所以所以函数的解析式为此时函数为正比例函数.
15. 解析:圆形地面被分成面积相等的八部分,其中阴影占四部分,所以小球落在黑色石子区域内的概率是.
16. 不公平 解析:画树状图如图所示,可知甲获胜的概率是,乙获胜的概率是,两个概率值不相等,故这个游戏不公平.
17. 解析:熟记函数图象的平移规律:左加右减,上加下减.
18. -3<<1 解析:根据抛物线的图象可知:抛物线的对称轴为直线,已知一个交点为(1,0),根据轴对称性,则另一个交点为(-3,0),所以时,的取值范围是-3<<1.
19.B 解析:由于反比例函数中的系数,所以只要点的两个坐标的乘积大于0即可,因此点B可能在反比例函数的图象上.
20. 解析:将木块随机投掷在水平桌面上,正方体的六个面都可能与桌面接触,因为A是正方体小木块三个面的交点,所以当这三个面中的任一面与桌面接触时,顶点A都与桌面接触.所以P(顶点A与桌面接触)==.
21.解:(1)把点的坐标代入中,得,所以.
将点,的坐标分别代入中,
得解得所以这个函数的解析式为.
(2)当时,所以点的坐标为.
(3)在中,当时,,所以,
所以△的面积为
22. 分析:本题考查了概率的计算与实际应用,利用列表法或树状图法列出两张牌的牌面数字之积的所有等可能结果,利用概率计算公式可求两张牌的牌面数字之积为奇数的概率.
解:
第一张牌牌面上的数字积第二张牌牌面上的数字 2 3
2 4 6
3 6 9
∴ P(积为奇数)=,P(积为偶数)=.
∴ 小明得分:×2=(分),小刚得分:×1=(分).
∵ ≠ ,∴ 这个游戏对双方不公平.
点拨:判断游戏的公平性关键是计算每个事件的概率,如果概率相等就公平,否则就不公平.此类题型一般通过比较概率的大小求解.
概率计算公式为:P(A)=.
23. 解:(1)∵点在的图象上,∴,∴.
又∵点在的图象上,,即 .
由点,在的图象上,知解得
所以反比例函数的解析式为,一次函数的解析式为.
(2)从图象上可知,当或时,反比例函数的值大于一次函数的值.
24.解:(1)依题意,设.
因为函数图象过和两点,
所以,,
所以,所以.
(2)当时,,
即该营销员5月份的收入为元.
25.解:(1)当时,设.
根据题意,得解得
所以当时,与之间的函数解析式是.
所以当时,.
当时,根据题意,得,即.
所以当时,与之间的函数解析式是.
(2)当时,与之间的函数解析式是.
解,得,
所以应从第45天开始进行人工灌溉.
26.解:(1)
(2)设袋中的红球有只,则有 或,解得.
所以袋中的红球有6只.
27.解:(1)由题意,知甲店有型产品件,
乙店有型产品件,有型产品件,
则.
由得
(2)由
所以有三种不同的分配方案:
①时,甲店型38件,型32件,乙店型2件,型28件;
②时,甲店型39件,型31件,乙店型1件,型29件;
③时,甲店型40件,型30件,乙店型0件,型30件.
(3)依题意,有
.
①若,当时,即甲店型40件,型30件,乙店型0件,型30件,能使总利润达到最大;
②若,当时,即符合题意的各种方案,使总利润都相同;
③若,当时,即甲店型10件,型60件,乙店型30件,型0件,能使总利润达到最大.
28. 解:(1)∵ 点P与P′(1,3)关于x轴对称,
∴ 点P的坐标为(1,﹣3).
∵ 抛物线y=a(x﹣1)2+c过点A(,0),顶点是P(1,﹣3),
∴ 解得
则抛物线的解析式为y=(x﹣1)2﹣3,
即y=x2﹣2x﹣2.
(2)∵ CD平行x轴,点P′(1,3)在CD上,
∴ C,D两点的纵坐标为3.
由(x﹣1)2﹣3=3,解得,,
∴ C,D两点的坐标分别为(,3),(,3).
∴ CD=.
∴ “W”图案的高与宽(CD)的比=.
O
x
y
第12题图
第18题图
同课章节目录
