函数的奇偶性及其应用(共11张PPT)
文档属性
| 名称 | 函数的奇偶性及其应用(共11张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 127.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-17 16:50:18 | ||
图片预览




文档简介
(共11张PPT)
函数奇偶性及其应用
知识点复习
1
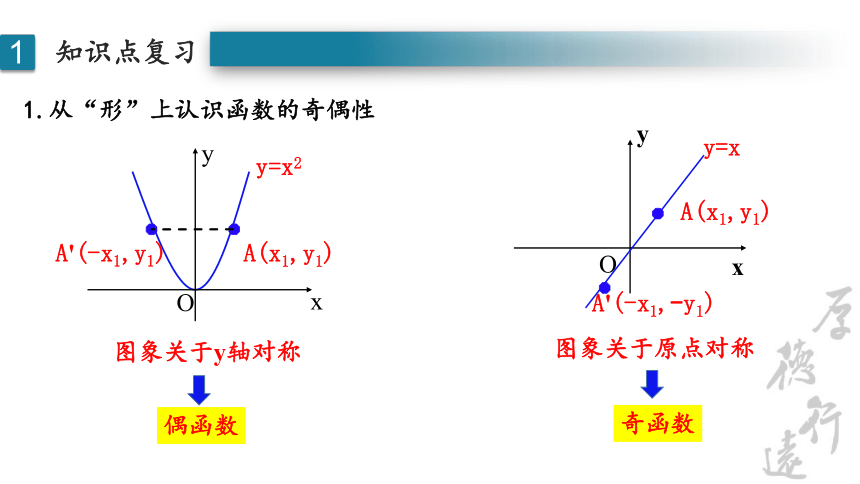
1.从“形”上认识函数的奇偶性
x
y
O
y=x
x
y
O
y=x2
图象关于y轴对称
图象关于原点对称
A(x1,y1)
A'(-x1,y1)
A(x1,y1)
A'(-x1,-y1)
偶函数
奇函数
知识点复习
1
(2)奇函数
2.函数的奇偶性的定义:
设函数y = f (x)的定义域为I
(1)偶函数
②f (x) = f (-x)
=f (|x|)
②-f (x) = f (-x)
①对于 x∈I,都有-x∈I
①对于 x∈I,都有-x∈I
定义域关于原点对称
定义域关于原点对称
图象关于y轴对称
图象关于原点对称
对于奇函数y=f(x),若0∈I,则必有f(0)=0;
巩固概念
判断正误.
①函数 f (x)=x2,x∈[0,+∞)是偶函数.( )
②对于函数y=f (x),若存在 x,使f (-x)=-f (x),则函数y=f (x)一定是奇函数.( )
③不存在既是奇函数,又是偶函数的函数.( )
④若f(x)是定义在R上的奇函数,则f(0)=0.( )
√
×
×
×
题型一 ——函数奇偶性的判断
一看
二算
三判
1.判断下列函数的奇偶性
1.若 f (x)=ax2-bx+1是定义域为[a,a+1]的偶函数,则a=____,b=____
题型二 ——函数奇偶性的应用
题型二 ——函数奇偶性的应用
2. 已知奇函数f(x)的定义域为[-5,5],且在区间[0,5]上的图象如图所示。
(1)画出在区间[-5,0]上的图象;
(2)写出使f (x)<0的x的取值集合.
题型二 ——函数奇偶性的应用
变式:已知函数 f (x)是R上的奇函数,且当x>0时,f (x)=x2+2x
(1)画出f (x)在R上的图象;
(2)写出使 f (x)<0的x的取值集合.
题型二 ——函数奇偶性的应用
3. 已知函数y=f (x)是定义在R上的偶函数,且当x ≥ 0时,f (x)=x2+2x+1
(1)求f (x)的解析式
(2)解不等式f (x) >4x+1
题型二 ——函数奇偶性的应用
4. 若定义在R上的偶函数f(x)和奇函数g(x),满足f(x)+g(x)=x2+3x+1,则f(x)解析式为________________
小结
4
1.函数的奇偶性的定义及图象:
2.判断函数的奇偶性的方法:
3.函数的奇偶性的应用:
函数奇偶性及其应用
知识点复习
1
1.从“形”上认识函数的奇偶性
x
y
O
y=x
x
y
O
y=x2
图象关于y轴对称
图象关于原点对称
A(x1,y1)
A'(-x1,y1)
A(x1,y1)
A'(-x1,-y1)
偶函数
奇函数
知识点复习
1
(2)奇函数
2.函数的奇偶性的定义:
设函数y = f (x)的定义域为I
(1)偶函数
②f (x) = f (-x)
=f (|x|)
②-f (x) = f (-x)
①对于 x∈I,都有-x∈I
①对于 x∈I,都有-x∈I
定义域关于原点对称
定义域关于原点对称
图象关于y轴对称
图象关于原点对称
对于奇函数y=f(x),若0∈I,则必有f(0)=0;
巩固概念
判断正误.
①函数 f (x)=x2,x∈[0,+∞)是偶函数.( )
②对于函数y=f (x),若存在 x,使f (-x)=-f (x),则函数y=f (x)一定是奇函数.( )
③不存在既是奇函数,又是偶函数的函数.( )
④若f(x)是定义在R上的奇函数,则f(0)=0.( )
√
×
×
×
题型一 ——函数奇偶性的判断
一看
二算
三判
1.判断下列函数的奇偶性
1.若 f (x)=ax2-bx+1是定义域为[a,a+1]的偶函数,则a=____,b=____
题型二 ——函数奇偶性的应用
题型二 ——函数奇偶性的应用
2. 已知奇函数f(x)的定义域为[-5,5],且在区间[0,5]上的图象如图所示。
(1)画出在区间[-5,0]上的图象;
(2)写出使f (x)<0的x的取值集合.
题型二 ——函数奇偶性的应用
变式:已知函数 f (x)是R上的奇函数,且当x>0时,f (x)=x2+2x
(1)画出f (x)在R上的图象;
(2)写出使 f (x)<0的x的取值集合.
题型二 ——函数奇偶性的应用
3. 已知函数y=f (x)是定义在R上的偶函数,且当x ≥ 0时,f (x)=x2+2x+1
(1)求f (x)的解析式
(2)解不等式f (x) >4x+1
题型二 ——函数奇偶性的应用
4. 若定义在R上的偶函数f(x)和奇函数g(x),满足f(x)+g(x)=x2+3x+1,则f(x)解析式为________________
小结
4
1.函数的奇偶性的定义及图象:
2.判断函数的奇偶性的方法:
3.函数的奇偶性的应用:
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
