鲁教版七年级数学2022-2023学年第一学期第一次阶段检测(pdf版无答案)
文档属性
| 名称 | 鲁教版七年级数学2022-2023学年第一学期第一次阶段检测(pdf版无答案) | 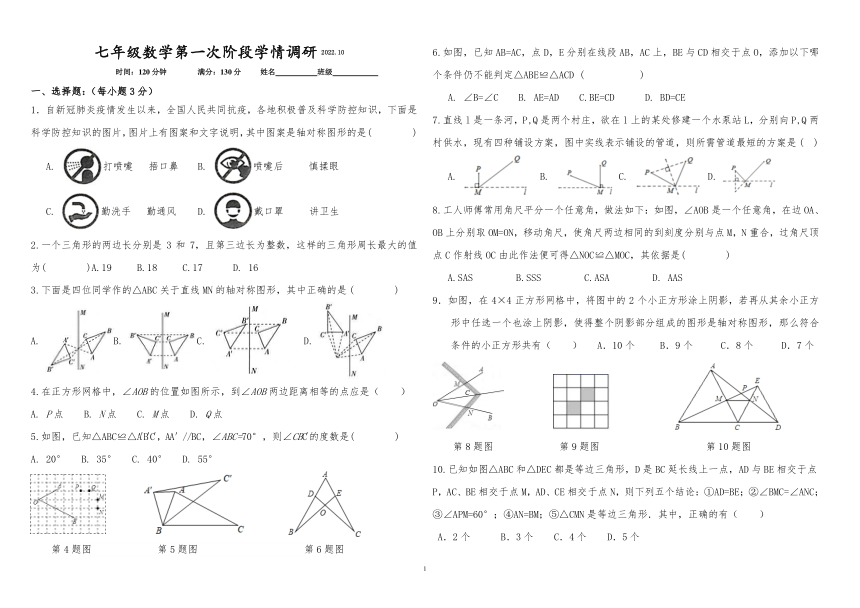 | |
| 格式 | |||
| 文件大小 | 566.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-16 17:15:41 | ||
图片预览

文档简介
七年级数学第一次阶段学情调研 2022.10 6.如图,已知 AB=AC,点 D,E分别在线段 AB,AC上,BE与 CD相交于点 O,添加以下哪
时间:120 分钟 满分:130 分 姓名 班级 个条件仍不能判定△ABE≌△ACD ( )
一、选择题:(每小题 3 分)
A. ∠B=∠C B. AE=AD C.BE=CD D. BD=CE
1.自新冠肺炎疫情发生以来,全国人民共同抗疫,各地积极普及科学防控知识,下面是
7.直线 l是一条河,P,Q是两个村庄,欲在 l上的某处修建一个水泵站 L,分别向 P,Q两
科学防控知识的图片,图片上有图案和文字说明,其中图案是轴对称图形的是( )
村供水,现有四种铺设方案,图中实线表示铺设的管道,则所需管道最短的方案是 ( )
A. 打喷嚏 捂口鼻 B. 喷嚏后 慎揉眼
A. B. C. D.
C. 勤洗手 勤通风 D. 戴口罩 讲卫生 8.工人师傅常用角尺平分一个任意角,做法如下:如图,∠AOB是一个任意角,在边 OA、
OB上分别取 OM=ON,移动角尺,使角尺两边相同的到刻度分别与点 M,N重合,过角尺顶
2.一个三角形的两边长分别是 3 和 7,且第三边长为整数,这样的三角形周长最大的值
点 C作射线 OC由此作法便可得△NOC≌△MOC,其依据是( )
为( )A.19 B.18 C.17 D. 16
A.SAS B.SSS C.ASA D. AAS
3.下面是四位同学作的△ABC关于直线 MN的轴对称图形,其中正确的是 ( )
9.如图,在 4×4 正方形网格中,将图中的 2 个小正方形涂上阴影,若再从其余小正方
形中任选一个也涂上阴影,使得整个阴影部分组成的图形是轴对称图形,那么符合
A. B. C. D. 条件的小正方形共有( ) A.10个 B.9个 C.8个 D.7个
4.在正方形网格中,∠AOB的位置如图所示,到∠AOB两边距离相等的点应是( )
A. P点 B. N点 C. M点 D. Q点
5.如图,已知△ABC≌△A′B′C′,AA′//BC,∠ABC=70°,则∠CBC′的度数是( )
第 8题图 第 9题图 第 10题图
A. 20° B. 35° C. 40° D. 55°
10.已知如图△ABC和△DEC都是等边三角形,D是 BC延长线上一点,AD与 BE相交于点
P,AC、BE相交于点 M,AD、CE相交于点 N,则下列五个结论:①AD=BE;②∠BMC=∠ANC;
③∠APM=60°;④AN=BM;⑤△CMN是等边三角形.其中,正确的有( )
A.2个 B.3个 C.4个 D.5个
第 4题图 第 5题图 第 6题图
1
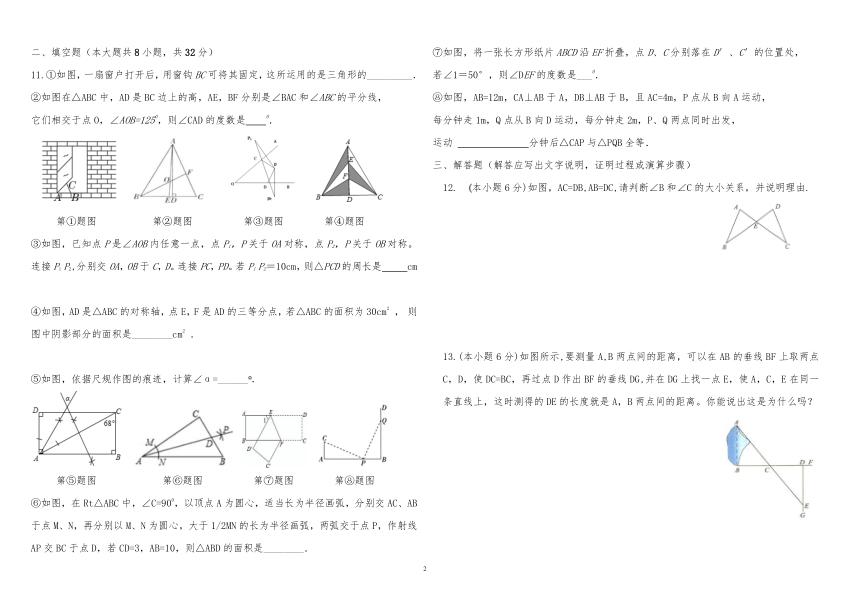
二、填空题(本大题共 8 小题,共 32分) ⑦如图,将一张长方形纸片 ABCD沿 EF折叠,点 D、C分别落在 D′、C′的位置处,
0
11.①如图,一扇窗户打开后,用窗钩 BC可将其固定,这所运用的是三角形的_________. 若∠1=50°,则∠DEF的度数是___.
②如图在△ABC中,AD是 BC边上的高,AE,BF分别是∠BAC和∠ABC的平分线, ⑧如图,AB=12m,CA⊥AB于 A,DB⊥AB于 B,且 AC=4m,P点从 B向 A运动,
它们相交于点 O,∠AOB=1250,则∠CAD的度数是 0. 每分钟走 1m,Q点从 B向 D运动,每分钟走 2m,P、Q两点同时出发,
运动 分钟后△CAP与△PQB全等.
三、解答题(解答应写出文字说明,证明过程或演算步骤)
12. 本小题 6分)如图,AC=DB,AB=DC,请判断∠B和∠C的大小关系,并说明理由.
第①题图 第②题图 第③题图 第④题图
③如图,已知点 P是∠AOB内任意一点,点 P1,P关于 OA对称,点 P2,P关于 OB对称。
连接 P1 P2,分别交 OA,OB于 C,D。连接 PC,PD。若 P1 P2=10cm,则△PCD的周长是 cm
④如图,AD是△ABC的对称轴,点 E,F是 AD的三等分点,若△ABC的面积为 30cm2 , 则
图中阴影部分的面积是________cm2 .
13.(本小题 6 分)如图所示,要测量 A,B 两点间的距离,可以在 AB 的垂线 BF 上取两点
⑤如图,依据尺规作图的痕迹,计算∠α=______ C,D,使 DC=BC,再过点 D作出 BF的垂线 DG,并在 DG上找一点 E,使 A,C,E在同一
条直线上,这时测得的 DE的长度就是 A,B两点间的距离。你能说出这是为什么吗?
第⑤题图 第⑥题图 第⑦题图 第⑧题图
⑥如图,在 Rt△ABC中,∠C=900,以顶点 A为圆心,适当长为半径画弧,分别交 AC、AB
于点 M、N,再分别以 M、N为圆心,大于 1/2MN的长为半径画弧,两弧交于点 P,作射线
AP交 BC于点 D,若 CD=3,AB=10,则△ABD的面积是________.
2
14.(本题 24分,每小题 6分) 15. 本小题 6 分 为了测量一幢楼高 AB,在旗杆 CD 与楼之间选定一点 P 测得旗杆顶 C 的
①如图是由四个完全相同的小正方形组成的 L 形图形,请你用三种方法分别在下面三个 视线 PC 与地面夹角∠DPC=38°,测楼顶 A 的视线 PA 与地面夹角∠APB=52°,量得点
图形上添画一个相同的小正方形,使它成为轴对称图形. P 到楼底的距离 PB 与旗杆高度都等于 8m,量得旗杆与楼之间的距离 DB=33m,计算楼高
AB是多少米?
②如下图所示,以虚线为对称轴画出图形的另一半.
以下题目请用直尺、圆规作图,不写作法,但要保留作图痕迹.
③已知:如图, 线段 a、b、∠α, 求作:△ABC, 使 BC=a,AB=b,∠ABC=∠α。 1 6 . . ( 本 小 题 8 分 如图,D是△ABC的边 AB上一点,CF//AB,DF交 AC于E点,DE=EF.
(1)求证:△ADE≌△CFE;
(2)若 AB=5,CF=4,求 BD的长.
a
b
④电信部门要修建一座电视信号发射塔,如图,按照设计要求,发射塔到两个城镇 A,B
的距离必须相等,到两条高速公路 OM,ON的距离也必须相等,发射塔 P应修建在什么位
置?
3
17.(本小题 8分 18.附加题(本小题 10分
如图,在△ABC中,AD,AF分别是△ABC的中线和高,BE是△ABD的角平分线. (1)如图 1,在△ABC 中,∠BAC=90°,AB=AC,直线 m 经过点 A,BD⊥m,CE⊥m,垂足
若△ABC的面积为 80,BD=10,求 AF的长; 分别为 D,E,求证:DE=BD+CE;
若∠BED=40°,∠BAD=25°,求∠BAF的大小.
如图 2,将 中的条件改为:在△ABC 中,AB=AC,D,A,E 三点都在直线 m 上,并且有
∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角,请问结论 DE=BD+CE 是否成立?
若成立,请你给出证明;若不成立,请说明理由;
4
时间:120 分钟 满分:130 分 姓名 班级 个条件仍不能判定△ABE≌△ACD ( )
一、选择题:(每小题 3 分)
A. ∠B=∠C B. AE=AD C.BE=CD D. BD=CE
1.自新冠肺炎疫情发生以来,全国人民共同抗疫,各地积极普及科学防控知识,下面是
7.直线 l是一条河,P,Q是两个村庄,欲在 l上的某处修建一个水泵站 L,分别向 P,Q两
科学防控知识的图片,图片上有图案和文字说明,其中图案是轴对称图形的是( )
村供水,现有四种铺设方案,图中实线表示铺设的管道,则所需管道最短的方案是 ( )
A. 打喷嚏 捂口鼻 B. 喷嚏后 慎揉眼
A. B. C. D.
C. 勤洗手 勤通风 D. 戴口罩 讲卫生 8.工人师傅常用角尺平分一个任意角,做法如下:如图,∠AOB是一个任意角,在边 OA、
OB上分别取 OM=ON,移动角尺,使角尺两边相同的到刻度分别与点 M,N重合,过角尺顶
2.一个三角形的两边长分别是 3 和 7,且第三边长为整数,这样的三角形周长最大的值
点 C作射线 OC由此作法便可得△NOC≌△MOC,其依据是( )
为( )A.19 B.18 C.17 D. 16
A.SAS B.SSS C.ASA D. AAS
3.下面是四位同学作的△ABC关于直线 MN的轴对称图形,其中正确的是 ( )
9.如图,在 4×4 正方形网格中,将图中的 2 个小正方形涂上阴影,若再从其余小正方
形中任选一个也涂上阴影,使得整个阴影部分组成的图形是轴对称图形,那么符合
A. B. C. D. 条件的小正方形共有( ) A.10个 B.9个 C.8个 D.7个
4.在正方形网格中,∠AOB的位置如图所示,到∠AOB两边距离相等的点应是( )
A. P点 B. N点 C. M点 D. Q点
5.如图,已知△ABC≌△A′B′C′,AA′//BC,∠ABC=70°,则∠CBC′的度数是( )
第 8题图 第 9题图 第 10题图
A. 20° B. 35° C. 40° D. 55°
10.已知如图△ABC和△DEC都是等边三角形,D是 BC延长线上一点,AD与 BE相交于点
P,AC、BE相交于点 M,AD、CE相交于点 N,则下列五个结论:①AD=BE;②∠BMC=∠ANC;
③∠APM=60°;④AN=BM;⑤△CMN是等边三角形.其中,正确的有( )
A.2个 B.3个 C.4个 D.5个
第 4题图 第 5题图 第 6题图
1
二、填空题(本大题共 8 小题,共 32分) ⑦如图,将一张长方形纸片 ABCD沿 EF折叠,点 D、C分别落在 D′、C′的位置处,
0
11.①如图,一扇窗户打开后,用窗钩 BC可将其固定,这所运用的是三角形的_________. 若∠1=50°,则∠DEF的度数是___.
②如图在△ABC中,AD是 BC边上的高,AE,BF分别是∠BAC和∠ABC的平分线, ⑧如图,AB=12m,CA⊥AB于 A,DB⊥AB于 B,且 AC=4m,P点从 B向 A运动,
它们相交于点 O,∠AOB=1250,则∠CAD的度数是 0. 每分钟走 1m,Q点从 B向 D运动,每分钟走 2m,P、Q两点同时出发,
运动 分钟后△CAP与△PQB全等.
三、解答题(解答应写出文字说明,证明过程或演算步骤)
12. 本小题 6分)如图,AC=DB,AB=DC,请判断∠B和∠C的大小关系,并说明理由.
第①题图 第②题图 第③题图 第④题图
③如图,已知点 P是∠AOB内任意一点,点 P1,P关于 OA对称,点 P2,P关于 OB对称。
连接 P1 P2,分别交 OA,OB于 C,D。连接 PC,PD。若 P1 P2=10cm,则△PCD的周长是 cm
④如图,AD是△ABC的对称轴,点 E,F是 AD的三等分点,若△ABC的面积为 30cm2 , 则
图中阴影部分的面积是________cm2 .
13.(本小题 6 分)如图所示,要测量 A,B 两点间的距离,可以在 AB 的垂线 BF 上取两点
⑤如图,依据尺规作图的痕迹,计算∠α=______ C,D,使 DC=BC,再过点 D作出 BF的垂线 DG,并在 DG上找一点 E,使 A,C,E在同一
条直线上,这时测得的 DE的长度就是 A,B两点间的距离。你能说出这是为什么吗?
第⑤题图 第⑥题图 第⑦题图 第⑧题图
⑥如图,在 Rt△ABC中,∠C=900,以顶点 A为圆心,适当长为半径画弧,分别交 AC、AB
于点 M、N,再分别以 M、N为圆心,大于 1/2MN的长为半径画弧,两弧交于点 P,作射线
AP交 BC于点 D,若 CD=3,AB=10,则△ABD的面积是________.
2
14.(本题 24分,每小题 6分) 15. 本小题 6 分 为了测量一幢楼高 AB,在旗杆 CD 与楼之间选定一点 P 测得旗杆顶 C 的
①如图是由四个完全相同的小正方形组成的 L 形图形,请你用三种方法分别在下面三个 视线 PC 与地面夹角∠DPC=38°,测楼顶 A 的视线 PA 与地面夹角∠APB=52°,量得点
图形上添画一个相同的小正方形,使它成为轴对称图形. P 到楼底的距离 PB 与旗杆高度都等于 8m,量得旗杆与楼之间的距离 DB=33m,计算楼高
AB是多少米?
②如下图所示,以虚线为对称轴画出图形的另一半.
以下题目请用直尺、圆规作图,不写作法,但要保留作图痕迹.
③已知:如图, 线段 a、b、∠α, 求作:△ABC, 使 BC=a,AB=b,∠ABC=∠α。 1 6 . . ( 本 小 题 8 分 如图,D是△ABC的边 AB上一点,CF//AB,DF交 AC于E点,DE=EF.
(1)求证:△ADE≌△CFE;
(2)若 AB=5,CF=4,求 BD的长.
a
b
④电信部门要修建一座电视信号发射塔,如图,按照设计要求,发射塔到两个城镇 A,B
的距离必须相等,到两条高速公路 OM,ON的距离也必须相等,发射塔 P应修建在什么位
置?
3
17.(本小题 8分 18.附加题(本小题 10分
如图,在△ABC中,AD,AF分别是△ABC的中线和高,BE是△ABD的角平分线. (1)如图 1,在△ABC 中,∠BAC=90°,AB=AC,直线 m 经过点 A,BD⊥m,CE⊥m,垂足
若△ABC的面积为 80,BD=10,求 AF的长; 分别为 D,E,求证:DE=BD+CE;
若∠BED=40°,∠BAD=25°,求∠BAF的大小.
如图 2,将 中的条件改为:在△ABC 中,AB=AC,D,A,E 三点都在直线 m 上,并且有
∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角,请问结论 DE=BD+CE 是否成立?
若成立,请你给出证明;若不成立,请说明理由;
4
同课章节目录
