人教版数学八年级下册 用平移坐标法探究平行四边形的存在问题 学案(含答案)
文档属性
| 名称 | 人教版数学八年级下册 用平移坐标法探究平行四边形的存在问题 学案(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 376.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-16 18:34:04 | ||
图片预览




文档简介
用平移坐标法探究平行四边形的存在问题
存在性问题是近年来各地中考的热点,其图形复杂,不确定因素较多,对学生的知识运用分析能力要求较高,有一定的难度.为此借用简单的平移坐标法来探究平行四边形的存在性问题.
1. 平移坐标法的探究
1.1 课本习题
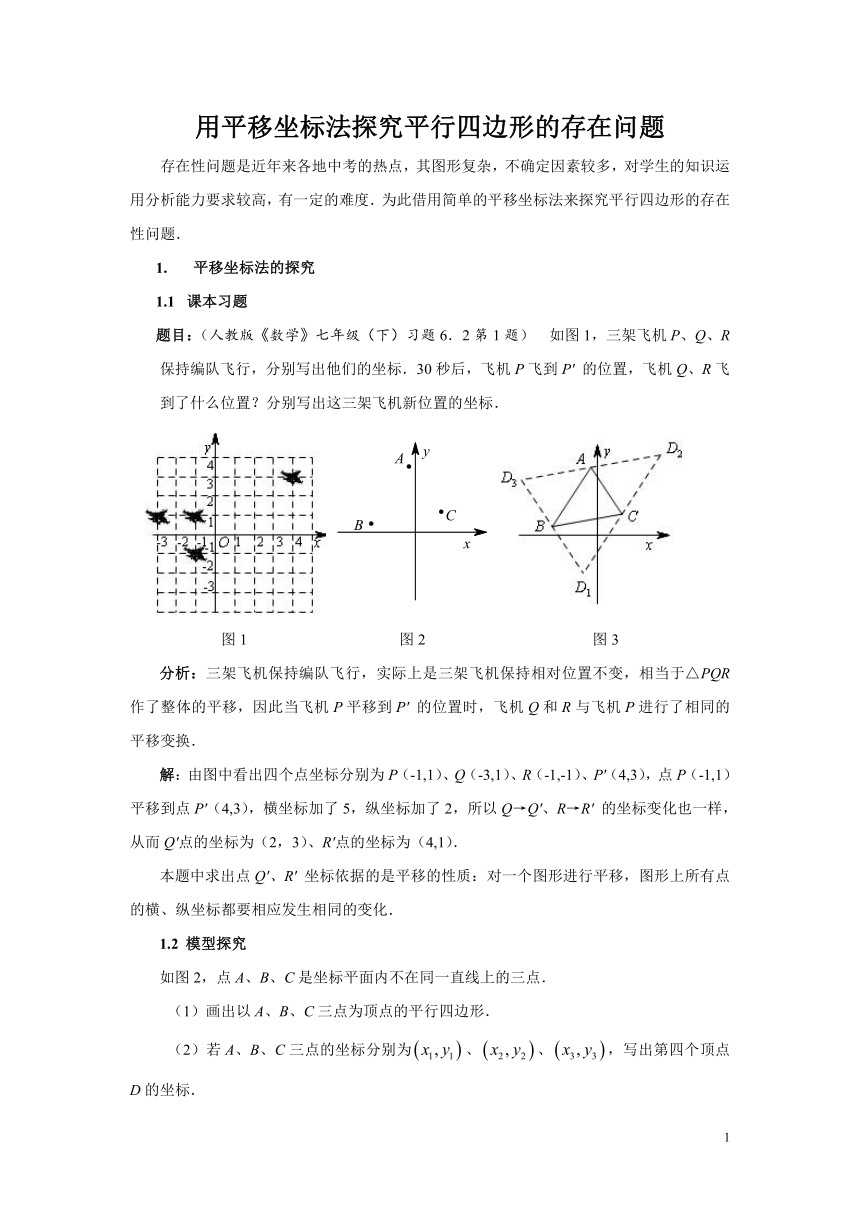
题目:(人教版《数学》七年级(下)习题6.2第1题) 如图1,三架飞机P、Q、R保持编队飞行,分别写出他们的坐标.30秒后,飞机P飞到P′ 的位置,飞机Q、R飞到了什么位置?分别写出这三架飞机新位置的坐标.
图1 图2 图3
分析:三架飞机保持编队飞行,实际上是三架飞机保持相对位置不变,相当于△PQR作了整体的平移,因此当飞机P平移到P′ 的位置时,飞机Q和R与飞机P进行了相同的平移变换.
解:由图中看出四个点坐标分别为P(-1,1)、Q(-3,1)、R(-1,-1)、P′(4,3),点P(-1,1)平移到点P′(4,3),横坐标加了5,纵坐标加了2,所以Q→Q′、R→R′ 的坐标变化也一样,从而Q′点的坐标为(2,3)、R′点的坐标为(4,1).
本题中求出点Q′、R′ 坐标依据的是平移的性质:对一个图形进行平移,图形上所有点的横、纵坐标都要相应发生相同的变化.
1.2 模型探究
如图2,点A、B、C是坐标平面内不在同一直线上的三点.
(1)画出以A、B、C三点为顶点的平行四边形.
(2)若A、B、C三点的坐标分别为、、,写出第四个顶点D的坐标.
解:(1)如图3, 过A、B、C分别作BC、AC、AB的平行线,则以A、B、C三点为顶点的平行四边形有三个:以BC为对角线,有□CABD1;以AC为对角线,有□ABCD2;以AB为对角线,有□ACBD3.
(2)在□CABD1中,线段AC平移到BD1,因A→B横坐标增加()、纵坐标增加(),根据坐标平移的性质得D1(,).
同理得D2(,)、D3(,).
结论:以不在同一直线上的三点为顶点的平行四边形有三个.由已知的三点坐标可根据图形平移的坐标性质,直接写出第四个顶点的坐标.姑且称之为平移坐标法.
2. 平移坐标法的运用
平移坐标法能否用来探究平行四边形的存在性问题呢?
2.1. 三个定点,一个动点,探究平行四边形的存在性.
例1 (2009烟台)如图4,抛物线与轴交于两点,与轴交于C点,且经过点(,),对称轴是直线,顶点是.
(1) 求抛物线对应的函数表达式;
(2) 经过两点作直线与轴交于点,在抛物线上是否存在这样的点,使以点P、A、C、N为顶点的四边形为平行四边形?
图4 图5
解:(1)抛物线的函数表达式为.
(2)由已知条件易探究得A、C、N三点坐标为A、 C、 N .
下面探讨以三点A、C、N为顶点的平行四边形的第四个顶点坐标. 如图5,由平移的性质直接写出第四个顶点的坐标:以CN为对角线,第四个顶点坐标为;以AC为对角线,第四个顶点坐标为;以AN为对角线,第四个顶点坐标为.将其分别代入抛物线中检验,其中只有在抛物线上.
点评:本题已知三个定点坐标的具体数值,可以根据坐标平移的性质直接写出第四个顶点的坐标.值得注意的是,若没有约定由三点构成的三条线段中哪条为边或对角线,则三种情况都必须考虑.
例2 (2009湖州)已知抛物线()与轴相交于点,顶点为.直线与轴相交于点,与直线相交于点.
(1) 填空:试用含的代数式分别表示点与的坐标,则;
(2) 如图6,在抛物线()上是否存在一点,使得以为顶点的四边形是平行四边形?
图6 图7
解:(1).
(2) 由已知条件易探究得A、C、N三点坐标为A、C、N .
下面探讨以A、C、N三点为顶点的平行四边形的第四个顶点的坐标,如图7.
若以CN为对角线,第四个顶点为,代入解析式得,即;
若以AC为对角线,第四个顶点为,代入解析式得,即;
若以AN为对角线,第四个顶点为,代入解析式得>0,不合题意,无解.
∴所以在抛物线上存在点和,使得以为顶点的四边形是平行四边形.
点评:①本题已知三个定点坐标,虽不是具体数值(含字母a),但依然可以根据坐标平移的性质直接写出第四个顶点的坐标.②看上去此法冗长,三种情况必须逐一探究,但思路简单,解题严谨.有些解法通过分析图形认为以AN为对角线显然不可能,其实对于学生来说这个“显然”并不显然.抛物线的走向和弯曲程度学生是难以判断的,更何况这是一个含字母系数的二次函数.这样讨论更严谨!
2.2 两个定点、两个动点,探究平行四边形的存在性。
例3 (2009抚顺) 已知:如图8,关于的抛物线与轴交于点、点,与轴交于点.
(1)求出此抛物线的解析式,并写出顶点坐标;
(2)在抛物线上有一点,使四边形为等腰梯形,写出点的坐标,并求出直线的解析式;
(3)在(2)中的直线交抛物线的对称轴于点,抛物线上有一动点,轴上有一动点.是否存在以为顶点的平行四边形?
解:(1)抛物线解析式为,顶点坐标是(2,4).
(2)点坐标为, 直线的解析式为.
图8 图9
(3)直线与抛物线对称轴的交点坐标为M(2,2).
假设轴上动点Q的坐标为.下面探讨以A、M、Q三点为顶点的平行四边形的第四个顶点坐标.(图9).
若以MQ为对角线,第四个顶点坐标为,代入得.
若以AM为对角线,第四个顶点坐标为,代入得.
若以AQ为对角线,第四个顶点坐标为,代入得.
∴存在满足条件的点有四个: , , ,
点评:先假设一个动点的坐标,将其看成一个定点,按照平移的性质,写出第四个顶点的坐标.再由另一动点应满足的条件,求出相应的坐标.
上述例题中总有两个点在同一坐标轴上,尚可通过平移和旋转来探究平行四边形的存在问题.如果题目中没有两点在同一坐标轴上,难么,难以通过分析图形的相互位置关系来探究平行四边形的存在问题.然而平移坐标法将是解决这一问题的一个法宝.(见附件)
例4 (2009南平)如图12,已知抛物线:
(1)求抛物线的顶点坐标.
(2)将向右平移2个单位,再向上平移1个单位,得到抛物线,求的解析式.
(3)抛物线的顶点为P,轴上有一动点M,在、这两条抛物线上是否存在点N,使O、P、M、N四点构成以OP为一边的平行四边形?
图12 图13
解:(1)的顶点坐标是(2,2)
(2)=
(3)假设轴上动点M坐标为.有已知条件易得P
下面探究以O、P、M三点为顶点(OP为边)的平行四边形第四个顶点N的坐标.
如图13,因为P为抛物线、的最高点,若以PM为对角线,有PN∥OM,则点N不可能在抛物线或上,故不可能存在满足条件的点;若以OM为对角线,用平移坐标法看出点N坐标为.
若点N 在抛物线上,可得:或;
若点N在抛物线上,可得:或.
∴存在满足条件的N点有四个:
、、、.
点评:①本题中N点可以在抛物线上,也可以在抛物线上,运动的范围较大,学生难以探索,用平移坐标法不必分析复杂的图形,降低了分析的难度,体现了平移坐标法强大的解题功效. ②本题中因确定了以OP为一边,所以只有两种情况需要探究.
3 平移坐标法的思考
平移坐标法不是探讨和论证线段的相等、三角形的全等……,而是用动态的观点看待几何图形——把平行四边形看成是由一条线段平移而成,用数的运算来描述图形的变化——用坐标表示平移,其本质是用几何变换去认识几何图形,用代数方法来解决几何问题,体现的是解析几何的思想、数形结合的思想、几何变换的思想.
平移坐标法的思路:先由题目条件探索三点的坐标(若只有两个定点,可设一个动点的坐标). 再画出以三点为顶点的平行四边形,根据坐标平移的性质写出第四个顶点的坐标.最后根据题目的要求(动点在什么曲线上),判断平行四边形的存在性.
平移坐标法的特点: ①不会遗漏. 平移坐标法回避了对复杂图形的相互关系的分析;②不需证明.平移坐标法直接写出第四个点的坐标,跨越了复杂的推理过程,回避了繁琐的证明;③不限条件.平移坐标法适用范围广,无论定点在什么位置、无论动点在哪几条曲线上、在什么曲线上,都可以探索,真正是以不变应万变.
由课本习题偶然发现可以通过平移直接写出点的坐标,于是笔者进一步研究发现,新课程把“平面直角坐标系”前移,同时新增了“用坐标表示平移”的内容,实际就是要用代数的方法研究几何问题,加强数形之间的联系,突出数形结合的思想.这启发我们在日常的教学活动中,要加强对新课程的研究,渗透新课程的理念,按照新课程的要求及时渗透数形结合的思想、几何变换的思想,引导学生从不同的角度思考问题,这样才能从教材简单的例、习题中获得解决问题的新方法、新思想,才能引导学生重视教材,同时培养学生探索的能力和创新的意识.
附:(2007·浙江义乌)如图10,抛物线与x轴交A、B两点(A点在B点左侧),直线与抛物线交于A、C两点,其中C点的横坐标为2.
(1)求A、B 两点的坐标及直线AC的函数表达式;
(2)点G是抛物线上的动点,在x轴上是否存在点F,使得以A、C、F、G这样四点为顶点的四边形是平行四边形?
图10 图11
变式 图11,若已知Q ,点G是抛物线上的动点,在抛物线上是否存在点F,使得以Q、C、F、G四点为顶点的四边形是平行四边形?
解题思路: 设F点坐标为(a, ),那么转化为三个定点问题,三个定点是Q ,C(2,-3),F(a, ),直接写出点G坐标,后代入中,就可求出a,从而知F点坐标。 也可设G点坐标,再写出F点坐标,代入也可。
PAGE
8
存在性问题是近年来各地中考的热点,其图形复杂,不确定因素较多,对学生的知识运用分析能力要求较高,有一定的难度.为此借用简单的平移坐标法来探究平行四边形的存在性问题.
1. 平移坐标法的探究
1.1 课本习题
题目:(人教版《数学》七年级(下)习题6.2第1题) 如图1,三架飞机P、Q、R保持编队飞行,分别写出他们的坐标.30秒后,飞机P飞到P′ 的位置,飞机Q、R飞到了什么位置?分别写出这三架飞机新位置的坐标.
图1 图2 图3
分析:三架飞机保持编队飞行,实际上是三架飞机保持相对位置不变,相当于△PQR作了整体的平移,因此当飞机P平移到P′ 的位置时,飞机Q和R与飞机P进行了相同的平移变换.
解:由图中看出四个点坐标分别为P(-1,1)、Q(-3,1)、R(-1,-1)、P′(4,3),点P(-1,1)平移到点P′(4,3),横坐标加了5,纵坐标加了2,所以Q→Q′、R→R′ 的坐标变化也一样,从而Q′点的坐标为(2,3)、R′点的坐标为(4,1).
本题中求出点Q′、R′ 坐标依据的是平移的性质:对一个图形进行平移,图形上所有点的横、纵坐标都要相应发生相同的变化.
1.2 模型探究
如图2,点A、B、C是坐标平面内不在同一直线上的三点.
(1)画出以A、B、C三点为顶点的平行四边形.
(2)若A、B、C三点的坐标分别为、、,写出第四个顶点D的坐标.
解:(1)如图3, 过A、B、C分别作BC、AC、AB的平行线,则以A、B、C三点为顶点的平行四边形有三个:以BC为对角线,有□CABD1;以AC为对角线,有□ABCD2;以AB为对角线,有□ACBD3.
(2)在□CABD1中,线段AC平移到BD1,因A→B横坐标增加()、纵坐标增加(),根据坐标平移的性质得D1(,).
同理得D2(,)、D3(,).
结论:以不在同一直线上的三点为顶点的平行四边形有三个.由已知的三点坐标可根据图形平移的坐标性质,直接写出第四个顶点的坐标.姑且称之为平移坐标法.
2. 平移坐标法的运用
平移坐标法能否用来探究平行四边形的存在性问题呢?
2.1. 三个定点,一个动点,探究平行四边形的存在性.
例1 (2009烟台)如图4,抛物线与轴交于两点,与轴交于C点,且经过点(,),对称轴是直线,顶点是.
(1) 求抛物线对应的函数表达式;
(2) 经过两点作直线与轴交于点,在抛物线上是否存在这样的点,使以点P、A、C、N为顶点的四边形为平行四边形?
图4 图5
解:(1)抛物线的函数表达式为.
(2)由已知条件易探究得A、C、N三点坐标为A、 C、 N .
下面探讨以三点A、C、N为顶点的平行四边形的第四个顶点坐标. 如图5,由平移的性质直接写出第四个顶点的坐标:以CN为对角线,第四个顶点坐标为;以AC为对角线,第四个顶点坐标为;以AN为对角线,第四个顶点坐标为.将其分别代入抛物线中检验,其中只有在抛物线上.
点评:本题已知三个定点坐标的具体数值,可以根据坐标平移的性质直接写出第四个顶点的坐标.值得注意的是,若没有约定由三点构成的三条线段中哪条为边或对角线,则三种情况都必须考虑.
例2 (2009湖州)已知抛物线()与轴相交于点,顶点为.直线与轴相交于点,与直线相交于点.
(1) 填空:试用含的代数式分别表示点与的坐标,则;
(2) 如图6,在抛物线()上是否存在一点,使得以为顶点的四边形是平行四边形?
图6 图7
解:(1).
(2) 由已知条件易探究得A、C、N三点坐标为A、C、N .
下面探讨以A、C、N三点为顶点的平行四边形的第四个顶点的坐标,如图7.
若以CN为对角线,第四个顶点为,代入解析式得,即;
若以AC为对角线,第四个顶点为,代入解析式得,即;
若以AN为对角线,第四个顶点为,代入解析式得>0,不合题意,无解.
∴所以在抛物线上存在点和,使得以为顶点的四边形是平行四边形.
点评:①本题已知三个定点坐标,虽不是具体数值(含字母a),但依然可以根据坐标平移的性质直接写出第四个顶点的坐标.②看上去此法冗长,三种情况必须逐一探究,但思路简单,解题严谨.有些解法通过分析图形认为以AN为对角线显然不可能,其实对于学生来说这个“显然”并不显然.抛物线的走向和弯曲程度学生是难以判断的,更何况这是一个含字母系数的二次函数.这样讨论更严谨!
2.2 两个定点、两个动点,探究平行四边形的存在性。
例3 (2009抚顺) 已知:如图8,关于的抛物线与轴交于点、点,与轴交于点.
(1)求出此抛物线的解析式,并写出顶点坐标;
(2)在抛物线上有一点,使四边形为等腰梯形,写出点的坐标,并求出直线的解析式;
(3)在(2)中的直线交抛物线的对称轴于点,抛物线上有一动点,轴上有一动点.是否存在以为顶点的平行四边形?
解:(1)抛物线解析式为,顶点坐标是(2,4).
(2)点坐标为, 直线的解析式为.
图8 图9
(3)直线与抛物线对称轴的交点坐标为M(2,2).
假设轴上动点Q的坐标为.下面探讨以A、M、Q三点为顶点的平行四边形的第四个顶点坐标.(图9).
若以MQ为对角线,第四个顶点坐标为,代入得.
若以AM为对角线,第四个顶点坐标为,代入得.
若以AQ为对角线,第四个顶点坐标为,代入得.
∴存在满足条件的点有四个: , , ,
点评:先假设一个动点的坐标,将其看成一个定点,按照平移的性质,写出第四个顶点的坐标.再由另一动点应满足的条件,求出相应的坐标.
上述例题中总有两个点在同一坐标轴上,尚可通过平移和旋转来探究平行四边形的存在问题.如果题目中没有两点在同一坐标轴上,难么,难以通过分析图形的相互位置关系来探究平行四边形的存在问题.然而平移坐标法将是解决这一问题的一个法宝.(见附件)
例4 (2009南平)如图12,已知抛物线:
(1)求抛物线的顶点坐标.
(2)将向右平移2个单位,再向上平移1个单位,得到抛物线,求的解析式.
(3)抛物线的顶点为P,轴上有一动点M,在、这两条抛物线上是否存在点N,使O、P、M、N四点构成以OP为一边的平行四边形?
图12 图13
解:(1)的顶点坐标是(2,2)
(2)=
(3)假设轴上动点M坐标为.有已知条件易得P
下面探究以O、P、M三点为顶点(OP为边)的平行四边形第四个顶点N的坐标.
如图13,因为P为抛物线、的最高点,若以PM为对角线,有PN∥OM,则点N不可能在抛物线或上,故不可能存在满足条件的点;若以OM为对角线,用平移坐标法看出点N坐标为.
若点N 在抛物线上,可得:或;
若点N在抛物线上,可得:或.
∴存在满足条件的N点有四个:
、、、.
点评:①本题中N点可以在抛物线上,也可以在抛物线上,运动的范围较大,学生难以探索,用平移坐标法不必分析复杂的图形,降低了分析的难度,体现了平移坐标法强大的解题功效. ②本题中因确定了以OP为一边,所以只有两种情况需要探究.
3 平移坐标法的思考
平移坐标法不是探讨和论证线段的相等、三角形的全等……,而是用动态的观点看待几何图形——把平行四边形看成是由一条线段平移而成,用数的运算来描述图形的变化——用坐标表示平移,其本质是用几何变换去认识几何图形,用代数方法来解决几何问题,体现的是解析几何的思想、数形结合的思想、几何变换的思想.
平移坐标法的思路:先由题目条件探索三点的坐标(若只有两个定点,可设一个动点的坐标). 再画出以三点为顶点的平行四边形,根据坐标平移的性质写出第四个顶点的坐标.最后根据题目的要求(动点在什么曲线上),判断平行四边形的存在性.
平移坐标法的特点: ①不会遗漏. 平移坐标法回避了对复杂图形的相互关系的分析;②不需证明.平移坐标法直接写出第四个点的坐标,跨越了复杂的推理过程,回避了繁琐的证明;③不限条件.平移坐标法适用范围广,无论定点在什么位置、无论动点在哪几条曲线上、在什么曲线上,都可以探索,真正是以不变应万变.
由课本习题偶然发现可以通过平移直接写出点的坐标,于是笔者进一步研究发现,新课程把“平面直角坐标系”前移,同时新增了“用坐标表示平移”的内容,实际就是要用代数的方法研究几何问题,加强数形之间的联系,突出数形结合的思想.这启发我们在日常的教学活动中,要加强对新课程的研究,渗透新课程的理念,按照新课程的要求及时渗透数形结合的思想、几何变换的思想,引导学生从不同的角度思考问题,这样才能从教材简单的例、习题中获得解决问题的新方法、新思想,才能引导学生重视教材,同时培养学生探索的能力和创新的意识.
附:(2007·浙江义乌)如图10,抛物线与x轴交A、B两点(A点在B点左侧),直线与抛物线交于A、C两点,其中C点的横坐标为2.
(1)求A、B 两点的坐标及直线AC的函数表达式;
(2)点G是抛物线上的动点,在x轴上是否存在点F,使得以A、C、F、G这样四点为顶点的四边形是平行四边形?
图10 图11
变式 图11,若已知Q ,点G是抛物线上的动点,在抛物线上是否存在点F,使得以Q、C、F、G四点为顶点的四边形是平行四边形?
解题思路: 设F点坐标为(a, ),那么转化为三个定点问题,三个定点是Q ,C(2,-3),F(a, ),直接写出点G坐标,后代入中,就可求出a,从而知F点坐标。 也可设G点坐标,再写出F点坐标,代入也可。
PAGE
8
