5.1导数的概念及其意义 课后习题及变式训练-2022-2023学年高二上学期数学人教A版(2019)选择性必修第二册(含答案)
文档属性
| 名称 | 5.1导数的概念及其意义 课后习题及变式训练-2022-2023学年高二上学期数学人教A版(2019)选择性必修第二册(含答案) | 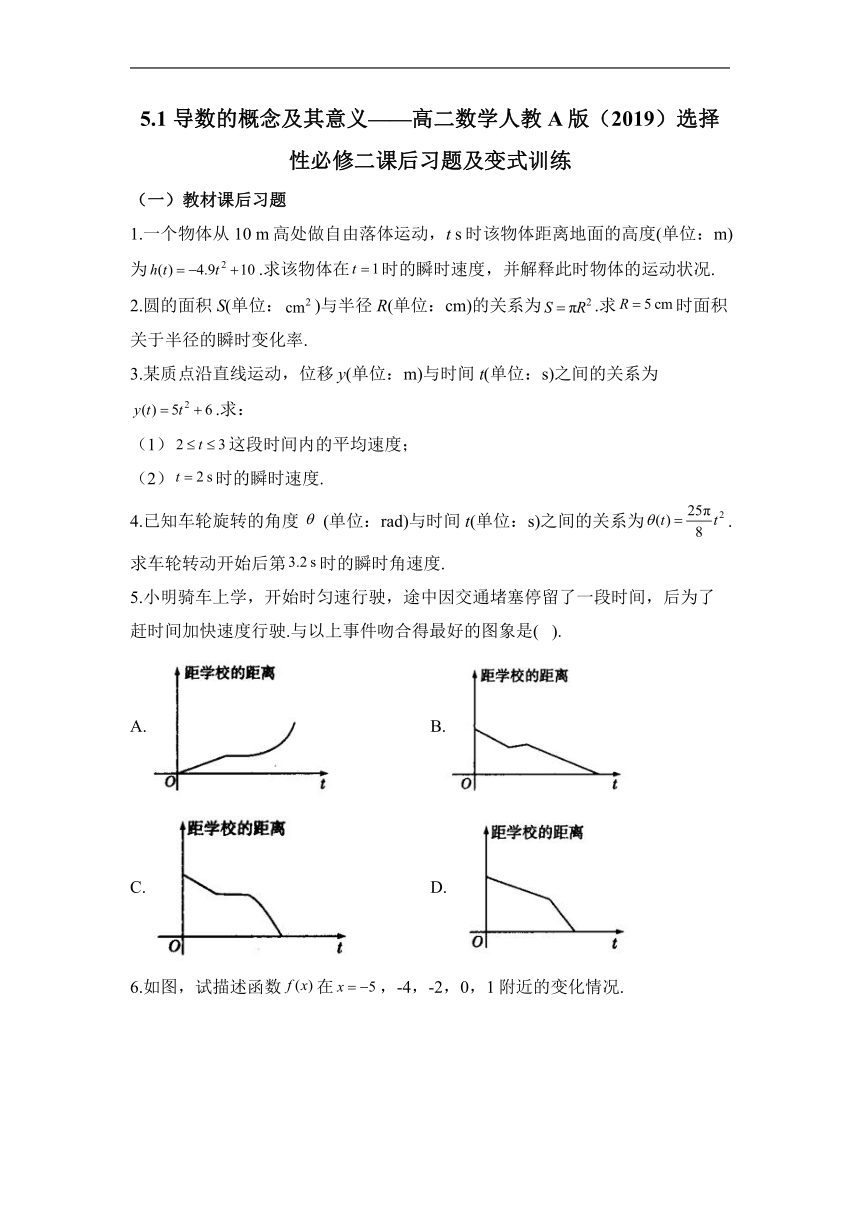 | |
| 格式 | docx | ||
| 文件大小 | 593.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-17 16:53:17 | ||
图片预览




文档简介
5.1 导数的概念及其意义——高二数学人教A版(2019)选择性必修二课后习题及变式训练
(一)教材课后习题
1.一个物体从10 m高处做自由落体运动,t s时该物体距离地面的高度(单位:m)为.求该物体在时的瞬时速度,并解释此时物体的运动状况.
2.圆的面积S(单位:)与半径R(单位:cm)的关系为.求时面积关于半径的瞬时变化率.
3.某质点沿直线运动,位移y(单位:m)与时间t(单位:s)之间的关系为.求:
(1)这段时间内的平均速度;
(2)时的瞬时速度.
4.已知车轮旋转的角度(单位:rad)与时间t(单位:s)之间的关系为.求车轮转动开始后第时的瞬时角速度.
5.小明骑车上学,开始时匀速行驶,途中因交通堵塞停留了一段时间,后为了赶时间加快速度行驶.与以上事件吻合得最好的图象是( ).
A. B.
C. D.
6.如图,试描述函数在,-4,-2,0,1附近的变化情况.
7.求曲线在点处的切线的倾斜角.
8.一个质量为的物体做直线运动,设位移y(单位:m)与时间t(单位:s)之间的关系为,并且物体的动能.求物体开始运动后第时的动能.
9.已知函数的图象,试画出其导函数图象的大致形状.
10.在高台跳水运动中,t s时运动员的重心相对于水面的高度(单位:m)是.高度h关于时间t的导数是速度v,速度v关于时间t的导数的物理意义是什么?试求v,关于时间t的函数解析式.
11.根据下列条件,分别画出函数的图象在这点附近的大致形状:
(1),;
(2),;
(3),.
(二)定点变式训练
12.若函数在处存在导数,则的值( )
A.与,h都有关 B.与有关,与h无关
C.与h有关,与无关 D.与,h都无关
13.设函数在点附近有定义,且,a,b为常数,则( ).
A. B. C. D.
14.我们常用函数的函数值的改变量与自变量的改变量的比值来表示平均变化率,当自变量x由改变到时,函数值的改变量等于( )
A. B. C. D.
15.已知与曲线相切,则实数a的值为( ).
A.-1 B.0 C.1 D.2
16.已知定义在R上的函数的图象在点处的切线为直线l,如图所示,则( )
A.
B.
C.
D.与的大小关系不确定
17.曲线的一条切线的斜率为2,则该切线的方程为________________.
18.已知函数,则函数在处的切线方程为__________.
19.函数在点处的切线方程为__________.
20.已知函数.
(1)求函数的导函数;
(2)过点作函数的图象的切线,求切线方程.
答案以及解析
1.答案:物体在附近大约以9.8 m/s的速度下落
解析:该物体在时的瞬时速度为
.
此时物体在附近大约以9.8 m/s的速度下落.
2.答案:
解析:时面积关于半径的瞬时变化率为
.
3、(1)答案:
解析:这段时间内的平均速度.
(2)答案:
解析:时的瞬时速度
.
4.答案:
解析:依题意有.
,
,
即车轮转动开始后第时的瞬时角速度为.
5.答案:C
解析:考查四个选项,横坐标表示时间,纵坐标表示距学校的距离,由此可知,图象应为下降趋势,A不符合,排除选项A.由题意可知,小明骑车上学,开始时匀速行驶可知图象开始一段是沿直线下降,又途中停留了一段时间,故此时有一段函数图象与x轴平行,D不符合,排除选项D.之后为了赶时间加快速度行驶,这一时间段图象下降速度的比一开始的下降速度快,因此B选项不正确,C选项正确.
6.答案:见解析
解析:函数在处切线的斜率,曲线是上升的,即函数在附近是单调递增的.
函数在处切线的斜率,曲线是上升的,即函数在附近是单调递增的.
函数在处斜率为0,所以函数在附近几乎没有变化.
函数在处切线的斜率,曲线是下降的,即函数在附近是单调递减的.
函数在处切线的斜率,曲线是下降的,即函数在附近是单调递减的.
7.答案:
解析:切线的斜率,
设切线倾斜角为,则,
又,.
8.答案:150 J
解析:,所以物体在第时的瞬时速度为,所以物体开始运动后第时的动能为.
9.答案:见解析
解析:第一个函数的图象是一条直线,其斜率是一个小于零的常数,因此,其函数的图象如图(1)所示.
第二个函数的导数恒大于零,并且随着x的增加,的值也在增加(如图(2)所示).
第三个函数,当x小于零时,小于零,当x大于零时,大于零,并且随着x的増加,的值也在增加(如图(3)所示).
以下给出了满足上述条件的导函数图像中的一种.
10.答案:见解析
解析:
.
,
.
11.答案:见解析
解析:由题意可知,函数的图象在点处的切线斜率为-1,所以此点附近曲线呈下降趋势,首先画出切线的图象,然后画出此点附近函数的图象.
同理可得(2)(3)某点处函数图象的大致形状.
下图是一种参考答案.
12.答案:B
解析:由导数的定义,知函数在处的导数与有关,与h无关.
13.答案:C
解析:由题意得,故选C.
14.答案:D
解析:自变量x由改变到,当时,,当时,,,故选D.
15.答案:B
解析:由题意,设切点为,所以,又因为,所以,所以,解得,故.故选B.
16.答案:A
解析:如图,设,则表示直线AB的斜率,表示函数的图象在点A处的切线的斜率,即直线l的斜率.
由图可知,,即,故选A.
17.答案:
解析:设切点为,对求导得,则曲线的切线的斜率为,解得.所以,则切点为,切线方程为,即.
18.答案:
解析:因为,所以切点坐标为,函数在处的切线斜率,所以所求的切线方程为,即.
19.答案:
解析:因为,所以,故,
所以函数在点处的切线方程为.
20.答案:(1)
,
当时,,
所以函数的导函数为.
(2)设切点为,则由(1),可得切线的斜率,则切线方程为,即.
因为切线过点,所以,解得或,从而切线方程为或.
解析:
(一)教材课后习题
1.一个物体从10 m高处做自由落体运动,t s时该物体距离地面的高度(单位:m)为.求该物体在时的瞬时速度,并解释此时物体的运动状况.
2.圆的面积S(单位:)与半径R(单位:cm)的关系为.求时面积关于半径的瞬时变化率.
3.某质点沿直线运动,位移y(单位:m)与时间t(单位:s)之间的关系为.求:
(1)这段时间内的平均速度;
(2)时的瞬时速度.
4.已知车轮旋转的角度(单位:rad)与时间t(单位:s)之间的关系为.求车轮转动开始后第时的瞬时角速度.
5.小明骑车上学,开始时匀速行驶,途中因交通堵塞停留了一段时间,后为了赶时间加快速度行驶.与以上事件吻合得最好的图象是( ).
A. B.
C. D.
6.如图,试描述函数在,-4,-2,0,1附近的变化情况.
7.求曲线在点处的切线的倾斜角.
8.一个质量为的物体做直线运动,设位移y(单位:m)与时间t(单位:s)之间的关系为,并且物体的动能.求物体开始运动后第时的动能.
9.已知函数的图象,试画出其导函数图象的大致形状.
10.在高台跳水运动中,t s时运动员的重心相对于水面的高度(单位:m)是.高度h关于时间t的导数是速度v,速度v关于时间t的导数的物理意义是什么?试求v,关于时间t的函数解析式.
11.根据下列条件,分别画出函数的图象在这点附近的大致形状:
(1),;
(2),;
(3),.
(二)定点变式训练
12.若函数在处存在导数,则的值( )
A.与,h都有关 B.与有关,与h无关
C.与h有关,与无关 D.与,h都无关
13.设函数在点附近有定义,且,a,b为常数,则( ).
A. B. C. D.
14.我们常用函数的函数值的改变量与自变量的改变量的比值来表示平均变化率,当自变量x由改变到时,函数值的改变量等于( )
A. B. C. D.
15.已知与曲线相切,则实数a的值为( ).
A.-1 B.0 C.1 D.2
16.已知定义在R上的函数的图象在点处的切线为直线l,如图所示,则( )
A.
B.
C.
D.与的大小关系不确定
17.曲线的一条切线的斜率为2,则该切线的方程为________________.
18.已知函数,则函数在处的切线方程为__________.
19.函数在点处的切线方程为__________.
20.已知函数.
(1)求函数的导函数;
(2)过点作函数的图象的切线,求切线方程.
答案以及解析
1.答案:物体在附近大约以9.8 m/s的速度下落
解析:该物体在时的瞬时速度为
.
此时物体在附近大约以9.8 m/s的速度下落.
2.答案:
解析:时面积关于半径的瞬时变化率为
.
3、(1)答案:
解析:这段时间内的平均速度.
(2)答案:
解析:时的瞬时速度
.
4.答案:
解析:依题意有.
,
,
即车轮转动开始后第时的瞬时角速度为.
5.答案:C
解析:考查四个选项,横坐标表示时间,纵坐标表示距学校的距离,由此可知,图象应为下降趋势,A不符合,排除选项A.由题意可知,小明骑车上学,开始时匀速行驶可知图象开始一段是沿直线下降,又途中停留了一段时间,故此时有一段函数图象与x轴平行,D不符合,排除选项D.之后为了赶时间加快速度行驶,这一时间段图象下降速度的比一开始的下降速度快,因此B选项不正确,C选项正确.
6.答案:见解析
解析:函数在处切线的斜率,曲线是上升的,即函数在附近是单调递增的.
函数在处切线的斜率,曲线是上升的,即函数在附近是单调递增的.
函数在处斜率为0,所以函数在附近几乎没有变化.
函数在处切线的斜率,曲线是下降的,即函数在附近是单调递减的.
函数在处切线的斜率,曲线是下降的,即函数在附近是单调递减的.
7.答案:
解析:切线的斜率,
设切线倾斜角为,则,
又,.
8.答案:150 J
解析:,所以物体在第时的瞬时速度为,所以物体开始运动后第时的动能为.
9.答案:见解析
解析:第一个函数的图象是一条直线,其斜率是一个小于零的常数,因此,其函数的图象如图(1)所示.
第二个函数的导数恒大于零,并且随着x的增加,的值也在增加(如图(2)所示).
第三个函数,当x小于零时,小于零,当x大于零时,大于零,并且随着x的増加,的值也在增加(如图(3)所示).
以下给出了满足上述条件的导函数图像中的一种.
10.答案:见解析
解析:
.
,
.
11.答案:见解析
解析:由题意可知,函数的图象在点处的切线斜率为-1,所以此点附近曲线呈下降趋势,首先画出切线的图象,然后画出此点附近函数的图象.
同理可得(2)(3)某点处函数图象的大致形状.
下图是一种参考答案.
12.答案:B
解析:由导数的定义,知函数在处的导数与有关,与h无关.
13.答案:C
解析:由题意得,故选C.
14.答案:D
解析:自变量x由改变到,当时,,当时,,,故选D.
15.答案:B
解析:由题意,设切点为,所以,又因为,所以,所以,解得,故.故选B.
16.答案:A
解析:如图,设,则表示直线AB的斜率,表示函数的图象在点A处的切线的斜率,即直线l的斜率.
由图可知,,即,故选A.
17.答案:
解析:设切点为,对求导得,则曲线的切线的斜率为,解得.所以,则切点为,切线方程为,即.
18.答案:
解析:因为,所以切点坐标为,函数在处的切线斜率,所以所求的切线方程为,即.
19.答案:
解析:因为,所以,故,
所以函数在点处的切线方程为.
20.答案:(1)
,
当时,,
所以函数的导函数为.
(2)设切点为,则由(1),可得切线的斜率,则切线方程为,即.
因为切线过点,所以,解得或,从而切线方程为或.
解析:
