人教版数学八年级上册 11.3.1 多边形课件(共22张PPT)
文档属性
| 名称 | 人教版数学八年级上册 11.3.1 多边形课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 337.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-16 19:27:52 | ||
图片预览







文档简介
(共22张PPT)
第十一章 三角形
第7课时 多边形
目录
01
本课目标
02
课堂导练
1.了解多边形的定义,认识多边形的边、内角、外角、顶点、对角线.
2.能区分凹多边形与凸多边形.
3.了解正多边形的概念.
本课目标
知识重点
知识点一:多边形的定义
(1)在平面内,由一些线段___________相接组成的封闭图形叫做多边形.
(2)如果一个多边形由_________ 组成,那么这个多边形叫做n边形.
(3)一个n边形有_____条边,_____个顶点,_____个内角.
首尾顺次
n条线段
n
n
n
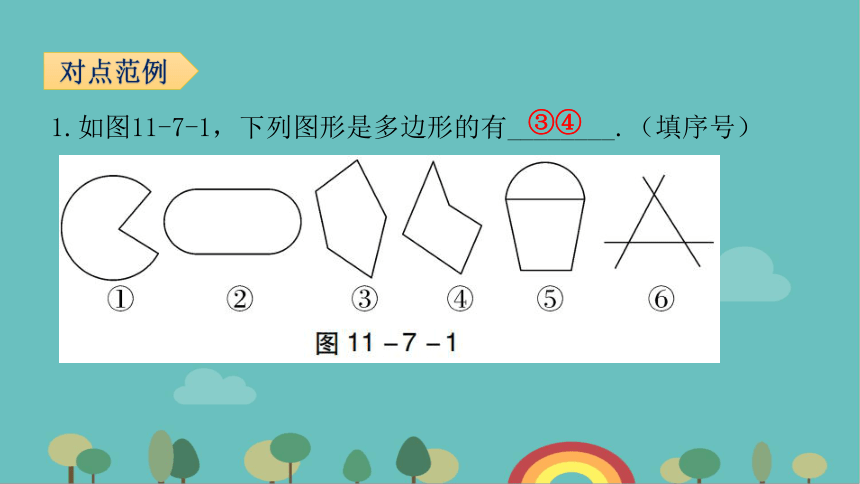
1.如图11-7-1,下列图形是多边形的有________.(填序号)
对点范例
③④
知识点二:对角线的定义
连接多边形__________的两个顶点的________,叫做多边形的对角线.
知识重点
不相邻
线段
2.从六边形的其中一个顶点出发,一共可以引出的对角线条数有( )
A.3条 B.4条 C.5条 D.6条
对点范例
A
知识点三:凸多边形的概念
画出多边形的任何一条边所在的直线,整个多边形都在这条直线的___________,这样的多边形叫做凸多边形.
知识重点
同一侧
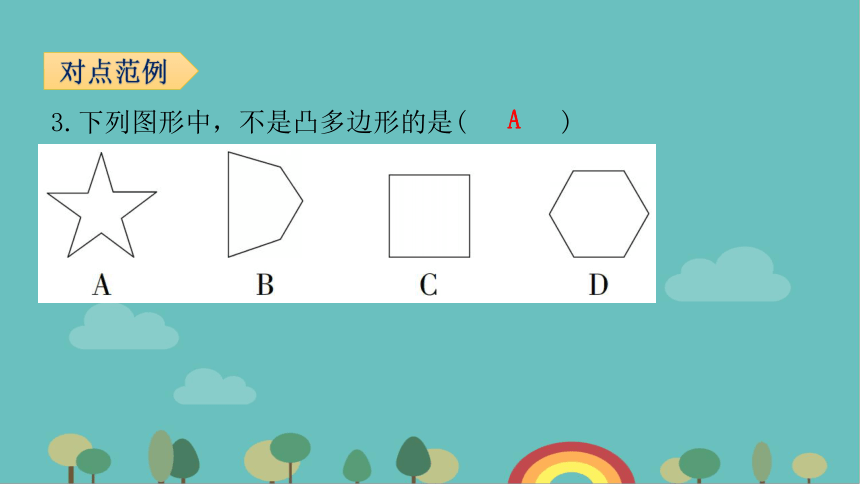
3.下列图形中,不是凸多边形的是( )
对点范例
A
知识点四:正多边形的概念
各个角都________,各条边都________的多边形叫做正多边形.
知识重点
相等
相等
4.下列图形为正多边形的是( )
对点范例
D
课堂导练
【例1】一个四边形用刀截去一个角后,它不可能是( )
A.三角形 B.四边形
C.五边形 D.六边形
思路点拨:根据截线经过的不同的位置可得剩余图形的相应的形状.
典型例题
D
1.若一个多边形截去一个角后变成了六边形,则原来多边形的边数可能是( )
A.5或6 B.6或7
C.5或6或7 D.6或7或8
举一反三
C
【例2】画出如图11-7-2所示的多边形的全部对角线.
典型例题
解:如答图11-7-1.
思路点拨:此图为五边形,根据多边形对角线的定义依次画出即可.
2.在凸多边形中,四边形的对角线有2条,五边形的对角线有5条,你认为凸九边形的对角线有多少条?写出你的思考过程.
举一反三
【例3】从一个五边形的同一顶点出发,分别连接这个顶点与其余各顶点,可以把这个五边形分成________个三角形.若是一个六边形,可以分割成________个三角形.
思路点拨:从n边形的一个顶点出发,连接这个点与其余各顶点,可以把一个多边形分割成(n-2)个三角形,依此作答.
典型例题
3
4
3.过多边形的一个顶点能引出7条对角线,则这个多边形的边数是________.
4.从某个多边形的一个顶点出发分别连接这个顶点与其他的顶点,可把这个多边形分成8个三角形,这个多边形是________边形.
举一反三
10
十
【例4】下列图形中,是正多边形的为( )
A.等腰三角形
B.长方形
C.正方形
D.五边都相等的五边形
思路点拨:根据正多边形的概念来解答.
典型例题
C
5.下列图形中,是正多边形的是( )
A.三条边都相等的三角形
B.四个角都是直角的四边形
C.四条边都相等的四边形
D.六条边都相等的六边形
举一反三
A
【例5】如图11-7-3,把同样大小的黑色棋子摆放在正多边形的边上,按照这样的规律摆下去,则第n个图形需要黑色棋子的个数是___________个.
思路点拨:先观察几个特殊图形,数出每个图形每条边上点的个数,再乘以边数,然后减去各个顶点的重复的点数,即可得出规律,从而解决问题.
典型例题
n(n+2)
6.某区园林工作者,为了把城市装扮得更加靓丽,用若干相同的花盆按一定的规律组成不同的正多边形图案(如图11-7-4),其中第1个图形一共有6个花盆,第2个图形一共有12个花盆,第3个图形一共有20个花盆……则第8个图形中一共有花盆的个数为( )
A.56 B.64
C.72 D.90
举一反三
D
谢 谢
第十一章 三角形
第7课时 多边形
目录
01
本课目标
02
课堂导练
1.了解多边形的定义,认识多边形的边、内角、外角、顶点、对角线.
2.能区分凹多边形与凸多边形.
3.了解正多边形的概念.
本课目标
知识重点
知识点一:多边形的定义
(1)在平面内,由一些线段___________相接组成的封闭图形叫做多边形.
(2)如果一个多边形由_________ 组成,那么这个多边形叫做n边形.
(3)一个n边形有_____条边,_____个顶点,_____个内角.
首尾顺次
n条线段
n
n
n
1.如图11-7-1,下列图形是多边形的有________.(填序号)
对点范例
③④
知识点二:对角线的定义
连接多边形__________的两个顶点的________,叫做多边形的对角线.
知识重点
不相邻
线段
2.从六边形的其中一个顶点出发,一共可以引出的对角线条数有( )
A.3条 B.4条 C.5条 D.6条
对点范例
A
知识点三:凸多边形的概念
画出多边形的任何一条边所在的直线,整个多边形都在这条直线的___________,这样的多边形叫做凸多边形.
知识重点
同一侧
3.下列图形中,不是凸多边形的是( )
对点范例
A
知识点四:正多边形的概念
各个角都________,各条边都________的多边形叫做正多边形.
知识重点
相等
相等
4.下列图形为正多边形的是( )
对点范例
D
课堂导练
【例1】一个四边形用刀截去一个角后,它不可能是( )
A.三角形 B.四边形
C.五边形 D.六边形
思路点拨:根据截线经过的不同的位置可得剩余图形的相应的形状.
典型例题
D
1.若一个多边形截去一个角后变成了六边形,则原来多边形的边数可能是( )
A.5或6 B.6或7
C.5或6或7 D.6或7或8
举一反三
C
【例2】画出如图11-7-2所示的多边形的全部对角线.
典型例题
解:如答图11-7-1.
思路点拨:此图为五边形,根据多边形对角线的定义依次画出即可.
2.在凸多边形中,四边形的对角线有2条,五边形的对角线有5条,你认为凸九边形的对角线有多少条?写出你的思考过程.
举一反三
【例3】从一个五边形的同一顶点出发,分别连接这个顶点与其余各顶点,可以把这个五边形分成________个三角形.若是一个六边形,可以分割成________个三角形.
思路点拨:从n边形的一个顶点出发,连接这个点与其余各顶点,可以把一个多边形分割成(n-2)个三角形,依此作答.
典型例题
3
4
3.过多边形的一个顶点能引出7条对角线,则这个多边形的边数是________.
4.从某个多边形的一个顶点出发分别连接这个顶点与其他的顶点,可把这个多边形分成8个三角形,这个多边形是________边形.
举一反三
10
十
【例4】下列图形中,是正多边形的为( )
A.等腰三角形
B.长方形
C.正方形
D.五边都相等的五边形
思路点拨:根据正多边形的概念来解答.
典型例题
C
5.下列图形中,是正多边形的是( )
A.三条边都相等的三角形
B.四个角都是直角的四边形
C.四条边都相等的四边形
D.六条边都相等的六边形
举一反三
A
【例5】如图11-7-3,把同样大小的黑色棋子摆放在正多边形的边上,按照这样的规律摆下去,则第n个图形需要黑色棋子的个数是___________个.
思路点拨:先观察几个特殊图形,数出每个图形每条边上点的个数,再乘以边数,然后减去各个顶点的重复的点数,即可得出规律,从而解决问题.
典型例题
n(n+2)
6.某区园林工作者,为了把城市装扮得更加靓丽,用若干相同的花盆按一定的规律组成不同的正多边形图案(如图11-7-4),其中第1个图形一共有6个花盆,第2个图形一共有12个花盆,第3个图形一共有20个花盆……则第8个图形中一共有花盆的个数为( )
A.56 B.64
C.72 D.90
举一反三
D
谢 谢
