1.1 空间向量及其运算(学生版无答案)
文档属性
| 名称 | 1.1 空间向量及其运算(学生版无答案) | 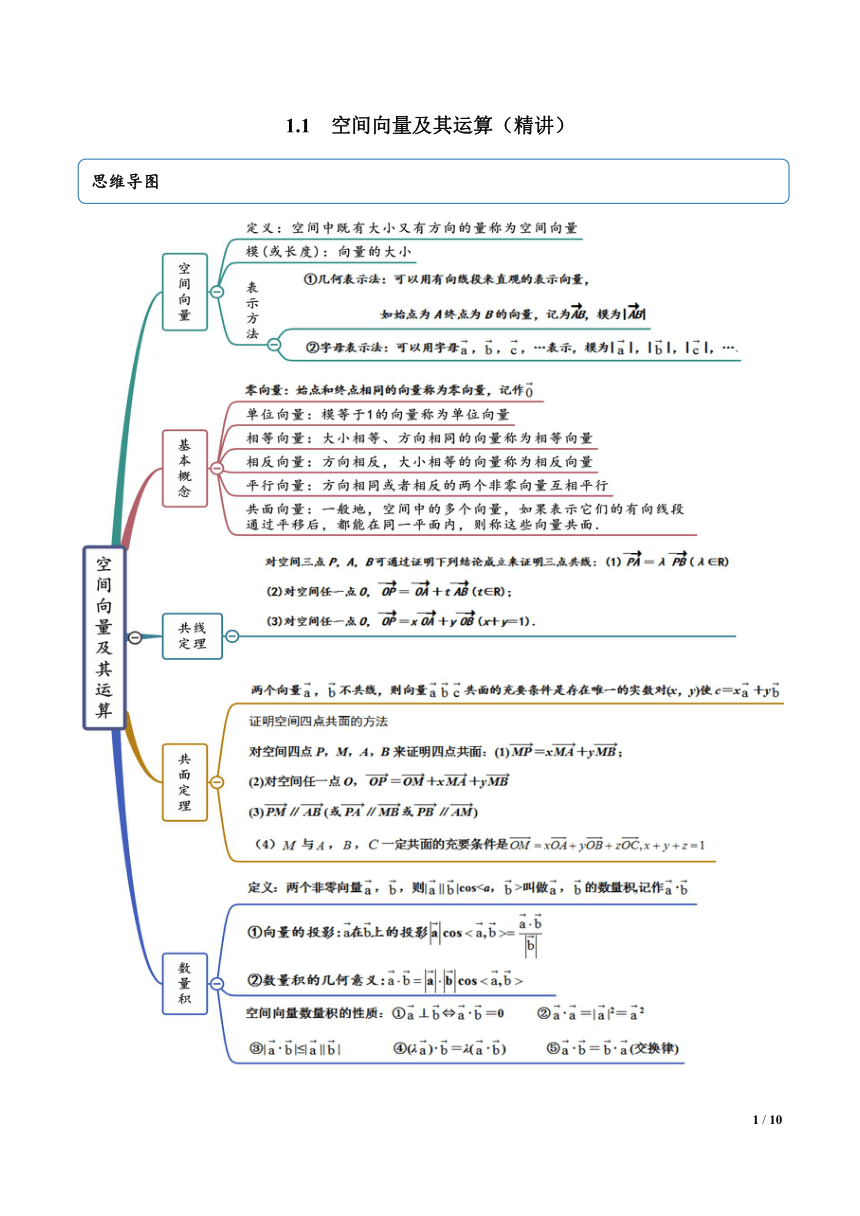 | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-17 18:07:07 | ||
图片预览




文档简介
1.1 空间向量及其运算(精讲)
(
思维导图
)
(
常见考法
)
考点一 概念辨析
【例1】(2021·全国高二课时练习)下列关于空间向量的说法中正确的是( )
A.若向量,平行,则,所在直线平行
B.若,则,的长度相等而方向相同或相反
C.若向量,满足,则
D.相等向量其方向必相同
【一隅三反】
1.(2021·全国高二课时练习)下列命题中,假命题是( )
A.同平面向量一样,任意两个空间向量都不能比较大小
B.两个相等的向量,若起点相同,则终点也相同
C.只有零向量的模等于0
D.共线的单位向量都相等
2.(2021·全国高二课时练习)下列说法:
①若两个空间向量相等,则表示它们有向线段的起点相同,终点也相同;
②若向量,满足,且与同向,则;
③若两个非零向量与满足,则,为相反向量;
④的充要条件是A与C重合,B与D重合.
其中错误的个数为( )
A.1 B.2 C.3 D.4
3.(2021·全国高二专题练习)在下列结论中:
①若向量共线,则向量所在的直线平行;
②若向量所在的直线为异面直线,则向量一定不共面;
③若三个向量两两共面,则向量共面;
④已知空间的三个向量,则对于空间的任意一个向量总存在实数x,y,z使得
.其中正确结论的个数是( )
A.0 B.1 C.2 D.3
考点二 共线共面问题
【例2-1】(1)(2020·全国高二课时练习)设,是空间两个不共线的向量,已知,,,且A,B,D三点共线,则k=________.
(2)(2021·全国高二)在下列条件中,使与,,一定共面的是( )
A. B.
C. D.
【例2-2】(2021·福建)如图,已知为空间的9个点,且, ,求证:
(1)四点共面,四点共面;
(2);
(3).
【一隅三反】
1.(2021·云南)已知为空间任意一点,若,则四点( )
A.一定不共面 B.一定共面 C.不一定共面 D.无法判断
2.(2021·河北)如图,在正方体ABCD-A1B1C1D1中,E在A1D1上,且,F在对角线A1C上,且,求证:E,F,B三点共线.
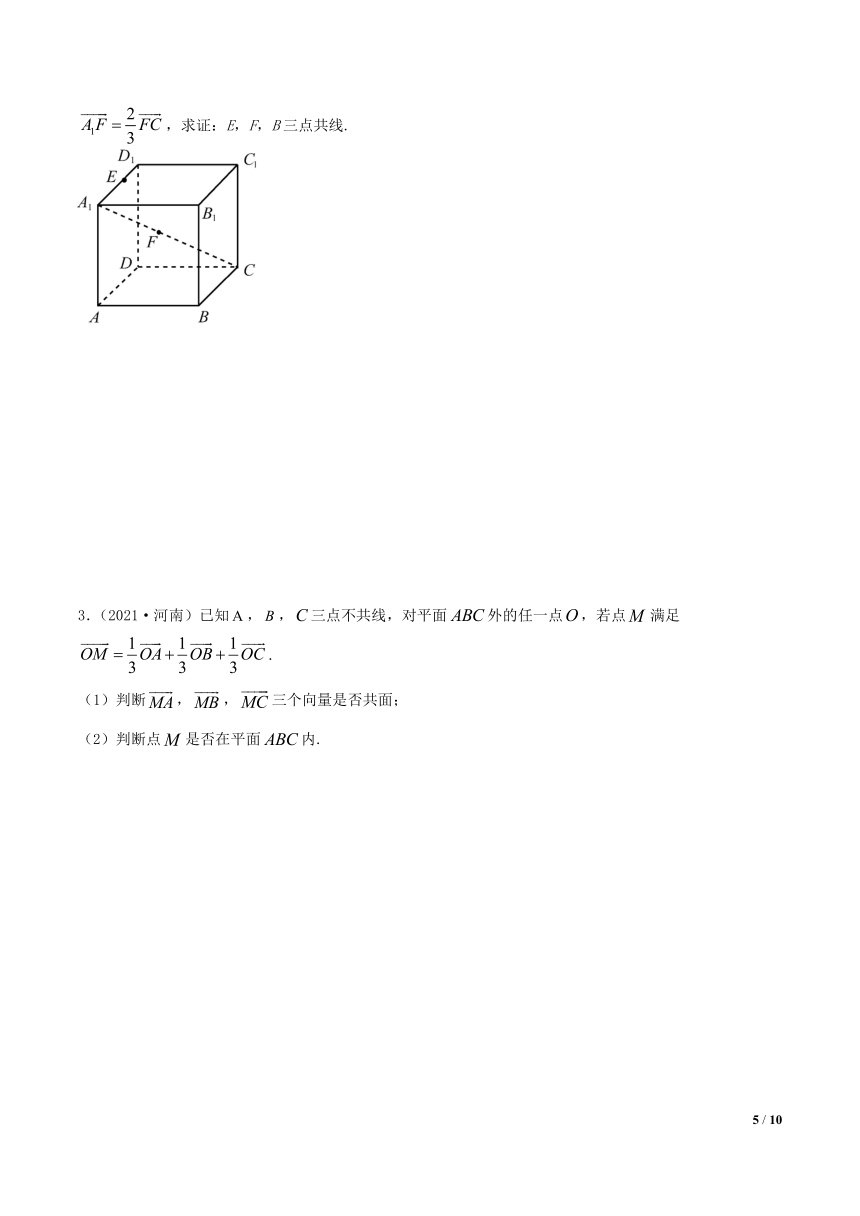
3.(2021·河南)已知,,三点不共线,对平面外的任一点,若点满足.
(1)判断,,三个向量是否共面;
(2)判断点是否在平面内.
考点三 空间向量的线性运算
【例3】(2021·山东)如图所示,在三棱柱中,是的中点,化简下列各式:
(1);
(2);
(3);
(4).
【一隅三反】
1.(2021·天津)已知M,G分别是空间四边形ABCD的两边BC,CD的中点,化简下列各式:
(1);
(2);
(3).
2.(2021·广东)如图所示,已知空间四边形ABCD,连接AC,BD,E,F,G分别是BC,CD,DB的中点,
请化简:(1)++;
(2)++.
3.(2021·全国高二课时练习)如图,已知四边形ABCD是空间四边形,E,H分别是边AB,AD的中点,F,G分别是边CB,CD上的点,且,.求证:四边形EFGH是梯形.
4.(2021·广东潮州)如图,在长方体中,E、F分别为棱、AB的中点.
(1)写出与向量相等的向量;
(2)写出与向量相反的向量;
(3)写出与向量平行的向量.
考点四 数量积
【例4】(2021·广东湛江)如图,在平行六面体中,,,,,.求:
(1); (2)的长; (3)的长.
【一隅三反】
1.(2021·宁夏银川市)如图,平行六面体,以顶点A为端点的三条棱长都为1,且两两夹角为,则的长为( )
A.1 B. C. D.3
2.(2021·宁夏)如图所示,在平行六面体中,AB=AD=A=1,∠AD=∠AB=∠BAD=60°,求:
(1)A的长;
(2)B的长.
3.(2021·云南)已知空间四边形OABC中,,且OA=OB=OC,M,N分别是OA,BC的中点,G是MN的中点,求证:OG⊥BC.
4.(2021·全国高二课时练习)如图所示,在空间四边形中,两两成角,且,为的中点,为的中点,试求间的距离.
10 / 10
(
思维导图
)
(
常见考法
)
考点一 概念辨析
【例1】(2021·全国高二课时练习)下列关于空间向量的说法中正确的是( )
A.若向量,平行,则,所在直线平行
B.若,则,的长度相等而方向相同或相反
C.若向量,满足,则
D.相等向量其方向必相同
【一隅三反】
1.(2021·全国高二课时练习)下列命题中,假命题是( )
A.同平面向量一样,任意两个空间向量都不能比较大小
B.两个相等的向量,若起点相同,则终点也相同
C.只有零向量的模等于0
D.共线的单位向量都相等
2.(2021·全国高二课时练习)下列说法:
①若两个空间向量相等,则表示它们有向线段的起点相同,终点也相同;
②若向量,满足,且与同向,则;
③若两个非零向量与满足,则,为相反向量;
④的充要条件是A与C重合,B与D重合.
其中错误的个数为( )
A.1 B.2 C.3 D.4
3.(2021·全国高二专题练习)在下列结论中:
①若向量共线,则向量所在的直线平行;
②若向量所在的直线为异面直线,则向量一定不共面;
③若三个向量两两共面,则向量共面;
④已知空间的三个向量,则对于空间的任意一个向量总存在实数x,y,z使得
.其中正确结论的个数是( )
A.0 B.1 C.2 D.3
考点二 共线共面问题
【例2-1】(1)(2020·全国高二课时练习)设,是空间两个不共线的向量,已知,,,且A,B,D三点共线,则k=________.
(2)(2021·全国高二)在下列条件中,使与,,一定共面的是( )
A. B.
C. D.
【例2-2】(2021·福建)如图,已知为空间的9个点,且, ,求证:
(1)四点共面,四点共面;
(2);
(3).
【一隅三反】
1.(2021·云南)已知为空间任意一点,若,则四点( )
A.一定不共面 B.一定共面 C.不一定共面 D.无法判断
2.(2021·河北)如图,在正方体ABCD-A1B1C1D1中,E在A1D1上,且,F在对角线A1C上,且,求证:E,F,B三点共线.
3.(2021·河南)已知,,三点不共线,对平面外的任一点,若点满足.
(1)判断,,三个向量是否共面;
(2)判断点是否在平面内.
考点三 空间向量的线性运算
【例3】(2021·山东)如图所示,在三棱柱中,是的中点,化简下列各式:
(1);
(2);
(3);
(4).
【一隅三反】
1.(2021·天津)已知M,G分别是空间四边形ABCD的两边BC,CD的中点,化简下列各式:
(1);
(2);
(3).
2.(2021·广东)如图所示,已知空间四边形ABCD,连接AC,BD,E,F,G分别是BC,CD,DB的中点,
请化简:(1)++;
(2)++.
3.(2021·全国高二课时练习)如图,已知四边形ABCD是空间四边形,E,H分别是边AB,AD的中点,F,G分别是边CB,CD上的点,且,.求证:四边形EFGH是梯形.
4.(2021·广东潮州)如图,在长方体中,E、F分别为棱、AB的中点.
(1)写出与向量相等的向量;
(2)写出与向量相反的向量;
(3)写出与向量平行的向量.
考点四 数量积
【例4】(2021·广东湛江)如图,在平行六面体中,,,,,.求:
(1); (2)的长; (3)的长.
【一隅三反】
1.(2021·宁夏银川市)如图,平行六面体,以顶点A为端点的三条棱长都为1,且两两夹角为,则的长为( )
A.1 B. C. D.3
2.(2021·宁夏)如图所示,在平行六面体中,AB=AD=A=1,∠AD=∠AB=∠BAD=60°,求:
(1)A的长;
(2)B的长.
3.(2021·云南)已知空间四边形OABC中,,且OA=OB=OC,M,N分别是OA,BC的中点,G是MN的中点,求证:OG⊥BC.
4.(2021·全国高二课时练习)如图所示,在空间四边形中,两两成角,且,为的中点,为的中点,试求间的距离.
10 / 10
