3.2.1 双曲线(第一课时)(学生版无答案)
文档属性
| 名称 | 3.2.1 双曲线(第一课时)(学生版无答案) | 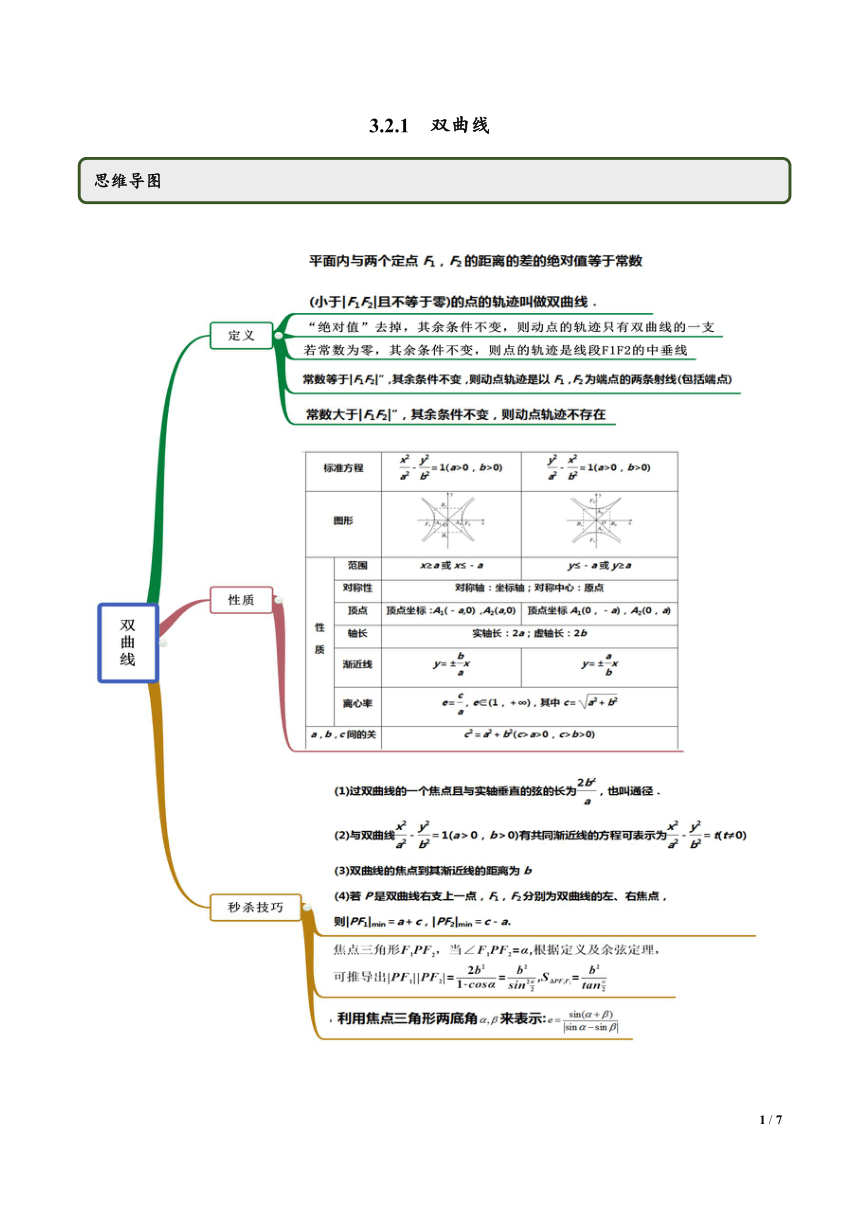 | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-17 18:10:54 | ||
图片预览

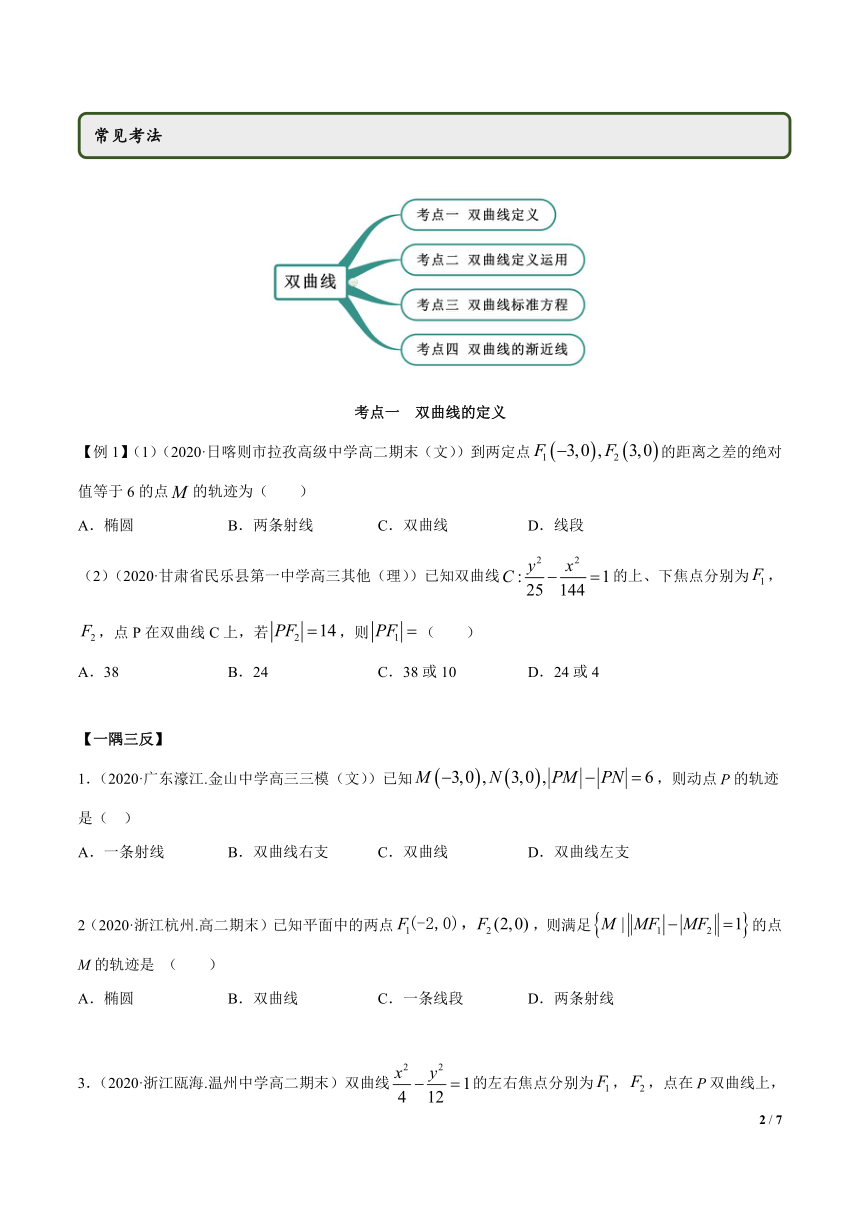

文档简介
3.2.1 双曲线
考点一 双曲线的定义
【例1】(1)(2020·日喀则市拉孜高级中学高二期末(文))到两定点的距离之差的绝对值等于6的点的轨迹为( )
A.椭圆 B.两条射线 C.双曲线 D.线段
(2)(2020·甘肃省民乐县第一中学高三其他(理))已知双曲线的上、下焦点分别为,,点P在双曲线C上,若,则( )
A.38 B.24 C.38或10 D.24或4
【一隅三反】
1.(2020·广东濠江.金山中学高三三模(文))已知,则动点的轨迹是( )
A.一条射线 B.双曲线右支 C.双曲线 D.双曲线左支
2(2020·浙江杭州.高二期末)已知平面中的两点,则满足的点M的轨迹是 ( )
A.椭圆 B.双曲线 C.一条线段 D.两条射线
3.(2020·浙江瓯海.温州中学高二期末)双曲线的左右焦点分别为,,点在双曲线上,若,则( )
A. B. C.或 D.
考点二 双曲线定义的运用
【例2】(1)(2020·江西高二期末(文))已知双曲线,直线l过其左焦点,交双曲线左支于A、B两点,且,为双曲线的右焦点,的周长为20,则m的值为 ( )
A.8 B.9 C.16 D.20
(2)(2020·四川南充.高二期末(理))设分别是双曲线的两个焦点,P是该双曲线上的一点,且,则的面积等于
A. B. C. D.
【一隅三反】
1.(2020·宁夏兴庆.银川九中)已知是双曲线的两个焦点,点为该双曲线上一点,若,且,则( )
A.1 B. C. D.3
2.(2020·武威第八中学高二期末(理))已知双曲线:的左右焦点分别为,为的右支上一点,且,则的面积等于
A. B. C. D.
3.(2020·吉林松原)已知点是双曲线上一点,,分别为双曲线的左 右焦点,若的外接圆半径为4,且为锐角,则( )
A.15 B.16 C.18 D.20
【例2-2】(2020·安徽贵池。池州一中高二期末(理))方程表示双曲线的充分不必要条件是( )
A. 或 B. C. D. 或
【一隅三反】
1.(2020·全国高二课时练习)若m为实数,则“”是“曲线C:表示双曲线”的( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
2.(2020·辽宁高三其他(理))若,则是方程表示双曲线的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
3.(2020·科尔沁左翼后旗甘旗卡第二高级中学高二期末(文))若曲线表示焦点在轴上的双曲线,则实数的取值范围为( )
A. B. C. D.
考点三 双曲线标准方程
【例3】(2019·吴起高级中学高二期末(理))在下列条件下求双曲线标准方程
(1)经过两点;
(2),经过点,焦点在轴上.
(3)过点(3,-),离心率e=;
(4)中心在原点,焦点F1,F2在坐标轴上,实轴长和虚轴长相等,且过点P(4,-).
【一隅三反】
1.(2019·重庆大足)焦点在轴上,实轴长为4,虚轴长为的双曲线的标准方程是( )
A. B. C. D.
2.(2020·四川高二期末(文))已知离心率为2的双曲线与椭圆有公共焦点,则双曲线的方程为( )
A. B.
C. D.
3.(2020·河南林州一中高二月考(理))已知双曲线的一条渐近线方程为,为该双曲线上一点,为其左、右焦点,且,,则该双曲线的方程为( )
A. B. C. D.
4.(2020·全国)已知是双曲线的左焦点,过作一条渐近线的垂线与右支交于点,垂足为,且,则双曲线方程为( )
A. B.
C. D.
考点四 渐近线
【例4】(2020·湖南开福)已知、分别为双曲线的左、右焦点,点在上,,则双曲线的渐近线方程为( )
A. B. C. D.
【一隅三反】
1.(2020·浙江柯桥)双曲线的渐近线方程为( )
A. B. C. D.
2.(2020·邢台市第八中学高二期末)双曲线的顶点到渐近线的距离是__________.
3.(2020·云南省下关第一中学)已知双曲线以椭圆的焦点为顶点,左右顶点为焦点,则的渐近线方程为( )
A. B. C. D.
5.(2020·全国高三三模(文))已知双曲线的左、右焦点分别为、,点在双曲线的右支上,点.若周长的最小值为,则双曲线的渐近线方程为________.
1 / 8
考点一 双曲线的定义
【例1】(1)(2020·日喀则市拉孜高级中学高二期末(文))到两定点的距离之差的绝对值等于6的点的轨迹为( )
A.椭圆 B.两条射线 C.双曲线 D.线段
(2)(2020·甘肃省民乐县第一中学高三其他(理))已知双曲线的上、下焦点分别为,,点P在双曲线C上,若,则( )
A.38 B.24 C.38或10 D.24或4
【一隅三反】
1.(2020·广东濠江.金山中学高三三模(文))已知,则动点的轨迹是( )
A.一条射线 B.双曲线右支 C.双曲线 D.双曲线左支
2(2020·浙江杭州.高二期末)已知平面中的两点,则满足的点M的轨迹是 ( )
A.椭圆 B.双曲线 C.一条线段 D.两条射线
3.(2020·浙江瓯海.温州中学高二期末)双曲线的左右焦点分别为,,点在双曲线上,若,则( )
A. B. C.或 D.
考点二 双曲线定义的运用
【例2】(1)(2020·江西高二期末(文))已知双曲线,直线l过其左焦点,交双曲线左支于A、B两点,且,为双曲线的右焦点,的周长为20,则m的值为 ( )
A.8 B.9 C.16 D.20
(2)(2020·四川南充.高二期末(理))设分别是双曲线的两个焦点,P是该双曲线上的一点,且,则的面积等于
A. B. C. D.
【一隅三反】
1.(2020·宁夏兴庆.银川九中)已知是双曲线的两个焦点,点为该双曲线上一点,若,且,则( )
A.1 B. C. D.3
2.(2020·武威第八中学高二期末(理))已知双曲线:的左右焦点分别为,为的右支上一点,且,则的面积等于
A. B. C. D.
3.(2020·吉林松原)已知点是双曲线上一点,,分别为双曲线的左 右焦点,若的外接圆半径为4,且为锐角,则( )
A.15 B.16 C.18 D.20
【例2-2】(2020·安徽贵池。池州一中高二期末(理))方程表示双曲线的充分不必要条件是( )
A. 或 B. C. D. 或
【一隅三反】
1.(2020·全国高二课时练习)若m为实数,则“”是“曲线C:表示双曲线”的( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
2.(2020·辽宁高三其他(理))若,则是方程表示双曲线的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
3.(2020·科尔沁左翼后旗甘旗卡第二高级中学高二期末(文))若曲线表示焦点在轴上的双曲线,则实数的取值范围为( )
A. B. C. D.
考点三 双曲线标准方程
【例3】(2019·吴起高级中学高二期末(理))在下列条件下求双曲线标准方程
(1)经过两点;
(2),经过点,焦点在轴上.
(3)过点(3,-),离心率e=;
(4)中心在原点,焦点F1,F2在坐标轴上,实轴长和虚轴长相等,且过点P(4,-).
【一隅三反】
1.(2019·重庆大足)焦点在轴上,实轴长为4,虚轴长为的双曲线的标准方程是( )
A. B. C. D.
2.(2020·四川高二期末(文))已知离心率为2的双曲线与椭圆有公共焦点,则双曲线的方程为( )
A. B.
C. D.
3.(2020·河南林州一中高二月考(理))已知双曲线的一条渐近线方程为,为该双曲线上一点,为其左、右焦点,且,,则该双曲线的方程为( )
A. B. C. D.
4.(2020·全国)已知是双曲线的左焦点,过作一条渐近线的垂线与右支交于点,垂足为,且,则双曲线方程为( )
A. B.
C. D.
考点四 渐近线
【例4】(2020·湖南开福)已知、分别为双曲线的左、右焦点,点在上,,则双曲线的渐近线方程为( )
A. B. C. D.
【一隅三反】
1.(2020·浙江柯桥)双曲线的渐近线方程为( )
A. B. C. D.
2.(2020·邢台市第八中学高二期末)双曲线的顶点到渐近线的距离是__________.
3.(2020·云南省下关第一中学)已知双曲线以椭圆的焦点为顶点,左右顶点为焦点,则的渐近线方程为( )
A. B. C. D.
5.(2020·全国高三三模(文))已知双曲线的左、右焦点分别为、,点在双曲线的右支上,点.若周长的最小值为,则双曲线的渐近线方程为________.
1 / 8
