北师大版高中数学必修第二册第一章三角函数5.2余弦函数的图象与性质再认识课件(共16张PPT)
文档属性
| 名称 | 北师大版高中数学必修第二册第一章三角函数5.2余弦函数的图象与性质再认识课件(共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-17 00:00:00 | ||
图片预览





文档简介
(共16张PPT)
5.2 余弦函数的图象与性质再认识
核心知识目标 核心素养目标
1.理解余弦函数图象的作法,知道余弦函数图象与正弦函数图象的关系.
2.掌握余弦函数的性质. 通过余弦函数图象的作法以及根据余弦函数图象得出余弦函数性质的过程,提高直观想象、数学抽象等核心素养.
知识探究·素养培育
探究点一
余弦函数的图象
[问题] 类比正弦函数图象的作法,如何作出余弦函数y=cos x,x∈R的
图象
提示:先用描点法作一个周期内的图象,再扩展到(-∞,+∞).
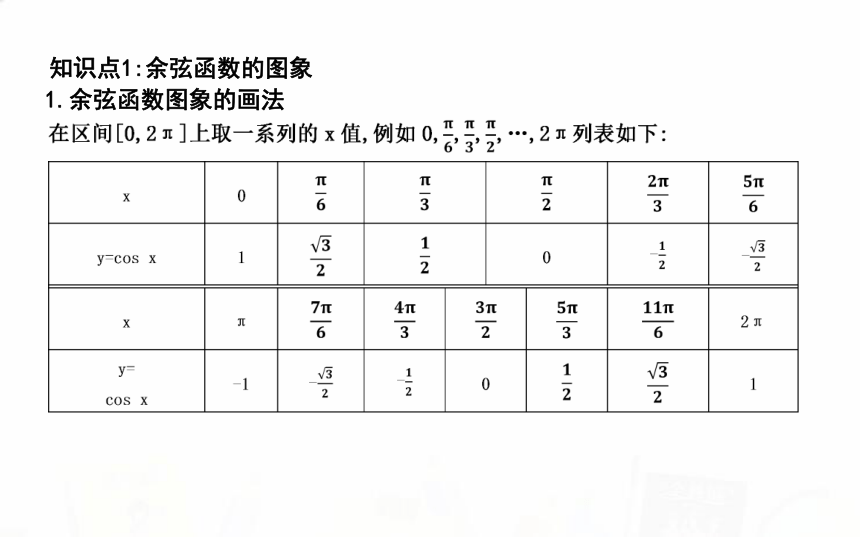
知识点1:余弦函数的图象
1.余弦函数图象的画法
利用表中的数据,先在平面直角坐标系内描点,结合对函数y=cos x性质的了解,用光滑曲线将它们顺次连接起来,就可以得到区间[0,2π]上y=cos x 的图象[如图(1)].
由周期性可知,函数y=cos x在区间[2kπ,2(k+1)π],k∈Z,k≠0上与在区间[0,2π]上的函数图象形状完全相同,只是位置不同.将函数y=cos x,x∈[0,2π]的图象向左、右平移(每次平移2π个单位长度),就可以得到余弦函数y=cos x,x∈R的图象[如图(2)].余弦函数y=cos x,x∈R的图象称作余弦曲线.
(0,1)
(π,-1)
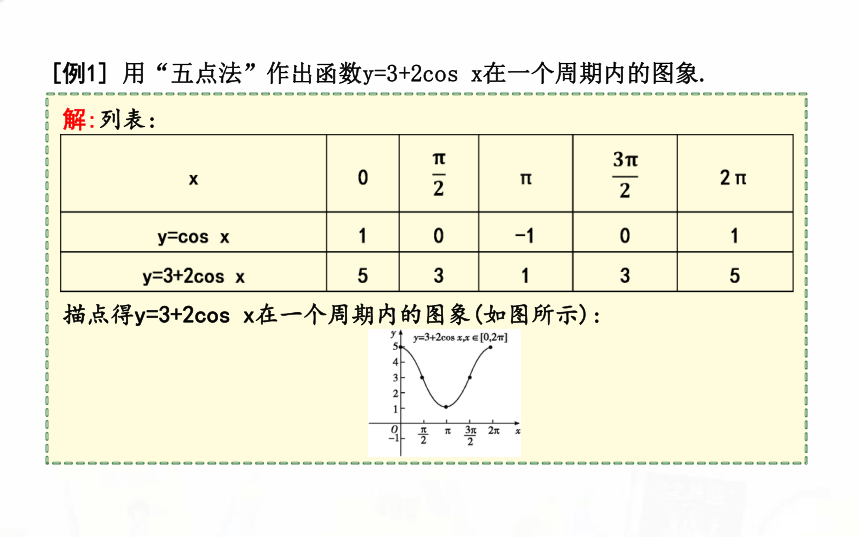
[例1] 用“五点法”作出函数y=3+2cos x在一个周期内的图象.
解:列表:
描点得y=3+2cos x在一个周期内的图象(如图所示):
方法总结
类似正弦函数图象,作余弦函数图象时也用“五点法”作出其一个周期内的图象,再根据周期性进行延展.
探究点二
余弦函数性质的再认识
知识点2:余弦函数的性质
函数
性质 y=cos x
定义域 R
值域 [-1,1]
奇偶性 偶函数
周期性 周期函数,最小正周期为2π
单调性 在每一个闭区间[2kπ-π,2kπ](k∈Z)上都单调递增;
在每一个闭区间[2kπ,2kπ+π](k∈Z)上都单调递减
最大值与
最小值 当x=2kπ(k∈Z)时取最大值1;
当x=2kπ+π(k∈Z)时取最小值-1
[思考] 观察余弦曲线,你能发现余弦曲线的对称性吗
变式训练2-1:比较大小(填“>”“<”或“=”).
(1)cos 15° cos 35°;
答案:(1)>
变式训练2-1:比较大小(填“>”“<”或“=”).
答案:(2)<
方法总结
(1)解含有正弦函数、余弦函数的不等式时,可以画出函数图象,从图象上得出不等式的解集;(2)利用余弦函数的单调性比较函数值大小时,要根据诱导公式把求解的函数值的自变量化到余弦函数的一个单调区间上,再利用余弦函数的单调性进行比较.
备用例题
[例3] 方程cos x=log8x的实数解的个数是( )
(A)4 (B)3 (C)2 (D)1
解析:分别画出函数y=cos x和y=log8x的图象,由图象可知两个函数的交点个数是3,
所以方程cos x=log8x的实数解的个数是3.
故选B.
5.2 余弦函数的图象与性质再认识
核心知识目标 核心素养目标
1.理解余弦函数图象的作法,知道余弦函数图象与正弦函数图象的关系.
2.掌握余弦函数的性质. 通过余弦函数图象的作法以及根据余弦函数图象得出余弦函数性质的过程,提高直观想象、数学抽象等核心素养.
知识探究·素养培育
探究点一
余弦函数的图象
[问题] 类比正弦函数图象的作法,如何作出余弦函数y=cos x,x∈R的
图象
提示:先用描点法作一个周期内的图象,再扩展到(-∞,+∞).
知识点1:余弦函数的图象
1.余弦函数图象的画法
利用表中的数据,先在平面直角坐标系内描点,结合对函数y=cos x性质的了解,用光滑曲线将它们顺次连接起来,就可以得到区间[0,2π]上y=cos x 的图象[如图(1)].
由周期性可知,函数y=cos x在区间[2kπ,2(k+1)π],k∈Z,k≠0上与在区间[0,2π]上的函数图象形状完全相同,只是位置不同.将函数y=cos x,x∈[0,2π]的图象向左、右平移(每次平移2π个单位长度),就可以得到余弦函数y=cos x,x∈R的图象[如图(2)].余弦函数y=cos x,x∈R的图象称作余弦曲线.
(0,1)
(π,-1)
[例1] 用“五点法”作出函数y=3+2cos x在一个周期内的图象.
解:列表:
描点得y=3+2cos x在一个周期内的图象(如图所示):
方法总结
类似正弦函数图象,作余弦函数图象时也用“五点法”作出其一个周期内的图象,再根据周期性进行延展.
探究点二
余弦函数性质的再认识
知识点2:余弦函数的性质
函数
性质 y=cos x
定义域 R
值域 [-1,1]
奇偶性 偶函数
周期性 周期函数,最小正周期为2π
单调性 在每一个闭区间[2kπ-π,2kπ](k∈Z)上都单调递增;
在每一个闭区间[2kπ,2kπ+π](k∈Z)上都单调递减
最大值与
最小值 当x=2kπ(k∈Z)时取最大值1;
当x=2kπ+π(k∈Z)时取最小值-1
[思考] 观察余弦曲线,你能发现余弦曲线的对称性吗
变式训练2-1:比较大小(填“>”“<”或“=”).
(1)cos 15° cos 35°;
答案:(1)>
变式训练2-1:比较大小(填“>”“<”或“=”).
答案:(2)<
方法总结
(1)解含有正弦函数、余弦函数的不等式时,可以画出函数图象,从图象上得出不等式的解集;(2)利用余弦函数的单调性比较函数值大小时,要根据诱导公式把求解的函数值的自变量化到余弦函数的一个单调区间上,再利用余弦函数的单调性进行比较.
备用例题
[例3] 方程cos x=log8x的实数解的个数是( )
(A)4 (B)3 (C)2 (D)1
解析:分别画出函数y=cos x和y=log8x的图象,由图象可知两个函数的交点个数是3,
所以方程cos x=log8x的实数解的个数是3.
故选B.
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
