3.2.2 双曲线(第二课时)(学生版)(无答案)
文档属性
| 名称 | 3.2.2 双曲线(第二课时)(学生版)(无答案) | 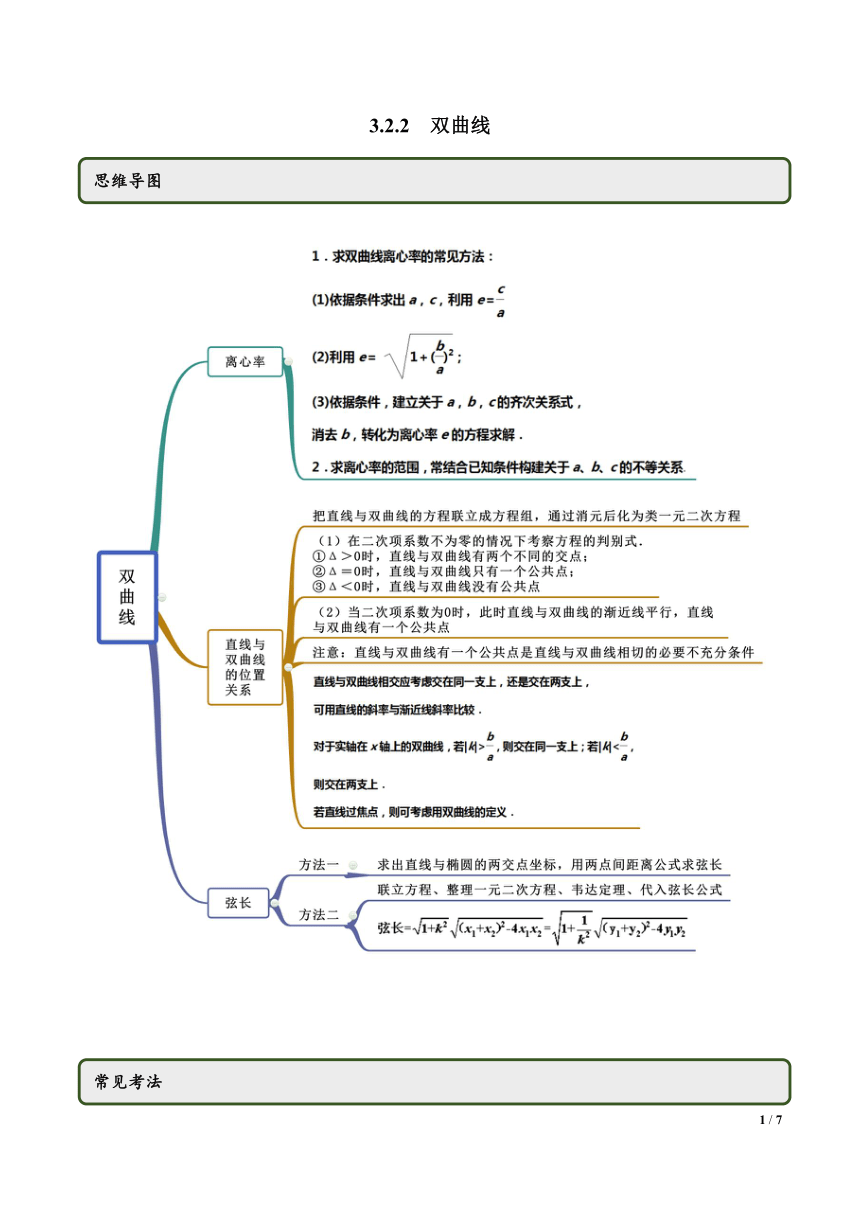 | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-17 18:40:38 | ||
图片预览


文档简介
3.2.2 双曲线
考点一 双曲线的离心率
【例1】(2020·云南省下关第一中学高二月考)若实数数列:1,,81成等比数列,则圆锥曲线的离心率是( )
A.或 B.或 C. D.或10
【一隅三反】
1.(2020·江苏南京)在平面直角坐标系xOy中,若点P(,0)到双曲线C:的一条渐近线的距离为6,则双曲线C的离心率为( )
A.2 B.4 C. D.
2.(2020·贵州省思南中学高二期末(理))已知、为双曲线:的左、右焦点,点为双曲线右支上一点,,,则双曲线的离心率为( )
A. B. C. D.
3.(2020·全国)已知,为双曲线的焦点,为与双由线的交点,且有,则该双曲线的离心率为( )
A. B. C. D.
4.(2020·沙坪坝.重庆八中高二月考)若双曲线(,)的一条渐近线经过点,则该双曲线的离心率为( )
A. B. C. D.
考点二 直线与双曲线的位置关系
【例2】已知双曲线x2-=1,问当直线l的斜率k为何值时,过点P(1,1)的直线l与双曲线只有一个公共点.
【一隅三反】
1.(2018·福建高二期末(理))若直线与双曲线的右支交于不同的两点,则的取值范围是
A. B.
C. D.
2.(2020·天水市第一中学高二月考(理))直线:与双曲线:的右支交于不同的两点,则斜率的取值范围是()
A. B. C. D.
3.(2020·四川资阳)直线l:kx-y-2k=0与双曲线x2-y2=2仅有一个公共点,则实数k的值为
A.-1或1 B.-1
C.1 D.1,-1,0
4.(2020·宁波市北仑中学高一期中)过双曲线2x2-y2=2的右焦点作直线l交双曲线于A,B两点,若|AB|=4,则这样的直线l的条数为( )
A.1 B.2
C.3 D.4
考点三 弦长
【例3】(2019·全国高三课时练习)过双曲线的右焦点F2,倾斜角为30°的直线交双曲线于A,B两点,O为坐标原点,F1为左焦点.
(1)求|AB|;
(2)求△AOB的面积.
【一隅三反】
1.(2020·全国)已知直线y=kx+1与双曲线交于A,B两点,且|AB|=8,则实数k的值为( )
A.± B.±或±
C.± D.±
2.(2018·全国高二课时练习)求双曲线被直线截得的弦长 .
3.(2020·邢台市第八中学高二期末)已知双曲线C:的离心率为,点是双曲线的一个顶点.
(1)求双曲线的方程;
(2)经过双曲线右焦点F2作倾斜角为30°的直线,直线与双曲线交于不同的两点A,B,求.
4.(2020·宾县第二中学高二期末(文))已知曲线及直线.
(1)若与左支交于两个不同的交点,求实数的取值范围;
(2)若与交于两点,是坐标原点,且的面积为,求实数的值.
考点四 点差法
【例4】(1)(2020·黑龙江南岗)已知双曲线:,斜率为2的直线与双曲线相交于点、,且弦中点坐标为,则双曲线的离心率为( )
A.2 B. C. D.3
(2)(2020·河南南阳.高二其他(文))直线经过且与双曲线交于,两点,如果点是线段的中点,那么直线的方程为( )
A. B.
C. D.不存在
(3)(2019·黑龙江大庆四中高二月考(理))已知双曲线与不过原点且不平行于坐标轴的直线相交于两点,线段的中点为,设直线的斜率为,直线的斜率为,则
A. B. C. D.
【一隅三反】
1.(2020·青海西宁)已知倾斜角为的直线与双曲线C:(,)相交于A,B两点,是弦的中点,则双曲线的离心率为( )
A. B. C. D.
2.(2020·湖北武汉)已知分别为双曲线实轴的左右两个端点,过双曲线的左焦点作直线交双曲线于两点(点异于),则直线的斜率之比( )
A. B. C. D.
3.(2019·会泽县第一中学校高二月考(理))点 平分双曲线 的一条弦,则这条弦所在直线的方程是__________.
8 / 8
考点一 双曲线的离心率
【例1】(2020·云南省下关第一中学高二月考)若实数数列:1,,81成等比数列,则圆锥曲线的离心率是( )
A.或 B.或 C. D.或10
【一隅三反】
1.(2020·江苏南京)在平面直角坐标系xOy中,若点P(,0)到双曲线C:的一条渐近线的距离为6,则双曲线C的离心率为( )
A.2 B.4 C. D.
2.(2020·贵州省思南中学高二期末(理))已知、为双曲线:的左、右焦点,点为双曲线右支上一点,,,则双曲线的离心率为( )
A. B. C. D.
3.(2020·全国)已知,为双曲线的焦点,为与双由线的交点,且有,则该双曲线的离心率为( )
A. B. C. D.
4.(2020·沙坪坝.重庆八中高二月考)若双曲线(,)的一条渐近线经过点,则该双曲线的离心率为( )
A. B. C. D.
考点二 直线与双曲线的位置关系
【例2】已知双曲线x2-=1,问当直线l的斜率k为何值时,过点P(1,1)的直线l与双曲线只有一个公共点.
【一隅三反】
1.(2018·福建高二期末(理))若直线与双曲线的右支交于不同的两点,则的取值范围是
A. B.
C. D.
2.(2020·天水市第一中学高二月考(理))直线:与双曲线:的右支交于不同的两点,则斜率的取值范围是()
A. B. C. D.
3.(2020·四川资阳)直线l:kx-y-2k=0与双曲线x2-y2=2仅有一个公共点,则实数k的值为
A.-1或1 B.-1
C.1 D.1,-1,0
4.(2020·宁波市北仑中学高一期中)过双曲线2x2-y2=2的右焦点作直线l交双曲线于A,B两点,若|AB|=4,则这样的直线l的条数为( )
A.1 B.2
C.3 D.4
考点三 弦长
【例3】(2019·全国高三课时练习)过双曲线的右焦点F2,倾斜角为30°的直线交双曲线于A,B两点,O为坐标原点,F1为左焦点.
(1)求|AB|;
(2)求△AOB的面积.
【一隅三反】
1.(2020·全国)已知直线y=kx+1与双曲线交于A,B两点,且|AB|=8,则实数k的值为( )
A.± B.±或±
C.± D.±
2.(2018·全国高二课时练习)求双曲线被直线截得的弦长 .
3.(2020·邢台市第八中学高二期末)已知双曲线C:的离心率为,点是双曲线的一个顶点.
(1)求双曲线的方程;
(2)经过双曲线右焦点F2作倾斜角为30°的直线,直线与双曲线交于不同的两点A,B,求.
4.(2020·宾县第二中学高二期末(文))已知曲线及直线.
(1)若与左支交于两个不同的交点,求实数的取值范围;
(2)若与交于两点,是坐标原点,且的面积为,求实数的值.
考点四 点差法
【例4】(1)(2020·黑龙江南岗)已知双曲线:,斜率为2的直线与双曲线相交于点、,且弦中点坐标为,则双曲线的离心率为( )
A.2 B. C. D.3
(2)(2020·河南南阳.高二其他(文))直线经过且与双曲线交于,两点,如果点是线段的中点,那么直线的方程为( )
A. B.
C. D.不存在
(3)(2019·黑龙江大庆四中高二月考(理))已知双曲线与不过原点且不平行于坐标轴的直线相交于两点,线段的中点为,设直线的斜率为,直线的斜率为,则
A. B. C. D.
【一隅三反】
1.(2020·青海西宁)已知倾斜角为的直线与双曲线C:(,)相交于A,B两点,是弦的中点,则双曲线的离心率为( )
A. B. C. D.
2.(2020·湖北武汉)已知分别为双曲线实轴的左右两个端点,过双曲线的左焦点作直线交双曲线于两点(点异于),则直线的斜率之比( )
A. B. C. D.
3.(2019·会泽县第一中学校高二月考(理))点 平分双曲线 的一条弦,则这条弦所在直线的方程是__________.
8 / 8
