12.2.3三角形全等的判定-ASA、AAS 教案
文档属性
| 名称 | 12.2.3三角形全等的判定-ASA、AAS 教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-16 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
12.2.3三角形全等的判定-ASA、AAS 教学设计
课题 12.2.3三角形全等的判定-ASA、AAS 单元 第12 单元 学科 数学 年级 八年级(上)
教材分析 经历探索三角形全等条件的过程,体会如何探索研究问题,让学生初步体会分类思想,提高分析问题和解决问题的能力.
核心素养分析 通过画图、比较、验证,培养学生注重观察,善于思考,不断总结的良好思维习惯.
学习目标 1.探索并正确理解三角形全等的判定方法“ASA”和“AAS”.2.会用三角形全等的判定方法“ASA”和“AAS”证明两个三角形全等.
重点 三角形全等“角边角”和“角角边”的条件.
难点 三角形全等“角边角”和“角角边”的条件.
教学过程
教学环节 教师活动 学生活动 设计意图
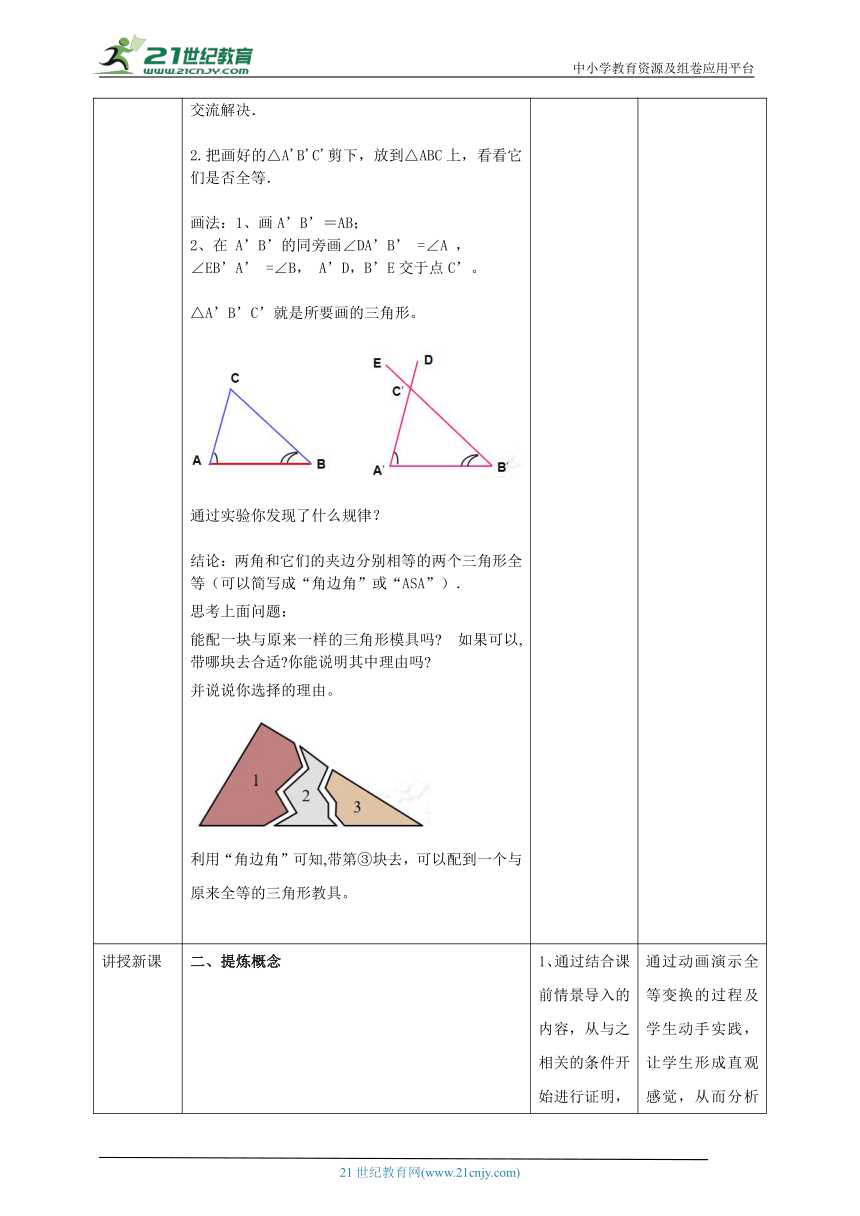
导入新课 一、创设情景,引出课题)思考:如图,小明不慎将一块三角形玻璃打碎为三块,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形模具吗 如果可以,带哪块去合适 你能说明其中理由吗 问题:根据我们前面的学习,想一想如果已知一个三角形的两角及一边,那么有几种可能的情况呢?“两角及夹边”“两角和其中一角的对边”是否上述两个条件都能判定两个三角形全等呢?下面通过我们的探究,你就会得出结论了:探究1: 1.先任意画出一个△ABC,再画一个△A'B'C',使A'B'=AB,∠A'=∠A,∠B'=∠B(即两角和它们的夹边对应相等). 学生先自己独立思考,动手画一画。在画的过程中若遇到不能解决的问题.可小组合作交流解决.2.把画好的△A'B'C'剪下,放到△ABC上,看看它们是否全等.画法:1、画A’B’=AB;2、在 A’B’的同旁画∠DA’B’ =∠A , ∠EB’A’ =∠B, A’D,B’E交于点C’。△A’B’C’就是所要画的三角形。通过实验你发现了什么规律?结论:两角和它们的夹边分别相等的两个三角形全等(可以简写成“角边角”或“ASA”).思考上面问题:能配一块与原来一样的三角形模具吗 如果可以,带哪块去合适 你能说明其中理由吗 并说说你选择的理由。利用“角边角”可知,带第③块去,可以配到一个与原来全等的三角形教具。 思考自议问题情境导入,使学生自然而然回忆之前学习过的内容,并对即将要学习的内容有一定的认识。 通过实际情境的分析,注重从一般到特殊,激发学生探究的兴趣,由此说明数学来源于生活。
讲授新课 提炼概念典例精讲例1、如图,D在AB上,E在AC上,AB=AC,∠B=∠C.求证:AD=AE. [分析]AD和AE分别在△ADC和△AEB中,所以要证AD=AE,只需证明△ADC≌△AEB即可. 证明:在△ADC和△AEB中 所以△ADC≌△AEB(ASA)所以AD=AE.探究2:在△ABC和△DEF中,∠A=∠D,∠B=∠E,BC=EF,△ABC与△DEF全等吗 能利用角边角条件证明你的结论吗 在△ABC和△DEF中,∠A +∠B +∠C=1800, ∠D +∠E +∠F =1800,∵ ∠A =∠D, ∠B=∠E, ∴ ∠C=∠F, 在ABC和DEF中∴ ∠B=∠E, BC=EF, ∠C=∠F, ∴ △ABC ≌△DEF (ASA)结论:两角和其中一个角的对边分别相等的两个三角形全等(可以简写成“角角边”或“AAS”).注意:这里的边是其中一角的对边,要注意区分!小结:现在为止,判定两个三角形全等我们已有了哪些方法 你能总结一下吗? 结论:SSS SAS ASA AAS(让学生自我总结、画图,然后教师在点评,一定要强调清楚SSA是不能判定全等的) 1、通过结合课前情景导入的内容,从与之相关的条件开始进行证明,学生自己动手,加深印象。2、学生动手,对两种条件进行比较,并回忆SAS的相关,进一步理解AAS与ASA。 通过动画演示全等变换的过程及学生动手实践,让学生形成直观感觉,从而分析总结出图形变换的本质,进一步加深对图形变换的理解,培养学生动态研究几何图形的意识。
课堂练习 四、巩固训练1. 如图,∠1=∠2,∠3=∠4,则判定△ABD和△ACD全等的依据是( )A. SSS B. ASA C. SAS D. AASB2. 在△ABC和△A′B′C′中,已知AB=A′B′,∠A=∠A′,∠C=∠C′,直接判定△ABC≌△A′B′C′的根据是 ( )A. SSS B. ASA C. AAS D. SASC3、如图,在下列条件中,不能直接证明△ABD≌△ACD的是( )A. BD=DC,AB=ACB. ∠ADB=∠ADC,BD=DCC. ∠B=∠C,∠BAD=∠CADD. ∠B=∠C,BD=DCD4.如图,∠B=∠DEF,AB=DE,要说明△ABC≌△DEF.(1)若以“SAS”为依据,还缺条件________________;(2)若以“ASA”为依据,还缺条件________________;(3)若以“AAS”为依据,还缺条件_____________________.(1)BC=EF (2)∠A=∠D (3)∠ACB=∠DFE5.如图,要测量池塘两岸相对的两点A,B的距离,可以在池塘外取AB的垂线BF上两点C,D,使BC=CD,再画出BF的垂线DE,使E与A,C在一条直线上,这时测得DE的长就是AB的长.为什么?解:∵ AB⊥BF,DE⊥BF, ∴ ∠ABC=∠EDC=90° ,在△ABC和△EDC中, ∴ △ABC≌△EDC (ASA) ,∴ AB=ED.6. 如图,已知∠D=∠E,AG=GD=CF=FE,A,B,C三点共线.求证:AB=CB.
课堂小结 课堂小结
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
12.2.3三角形全等的判定-ASA、AAS 教学设计
课题 12.2.3三角形全等的判定-ASA、AAS 单元 第12 单元 学科 数学 年级 八年级(上)
教材分析 经历探索三角形全等条件的过程,体会如何探索研究问题,让学生初步体会分类思想,提高分析问题和解决问题的能力.
核心素养分析 通过画图、比较、验证,培养学生注重观察,善于思考,不断总结的良好思维习惯.
学习目标 1.探索并正确理解三角形全等的判定方法“ASA”和“AAS”.2.会用三角形全等的判定方法“ASA”和“AAS”证明两个三角形全等.
重点 三角形全等“角边角”和“角角边”的条件.
难点 三角形全等“角边角”和“角角边”的条件.
教学过程
教学环节 教师活动 学生活动 设计意图
导入新课 一、创设情景,引出课题)思考:如图,小明不慎将一块三角形玻璃打碎为三块,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形模具吗 如果可以,带哪块去合适 你能说明其中理由吗 问题:根据我们前面的学习,想一想如果已知一个三角形的两角及一边,那么有几种可能的情况呢?“两角及夹边”“两角和其中一角的对边”是否上述两个条件都能判定两个三角形全等呢?下面通过我们的探究,你就会得出结论了:探究1: 1.先任意画出一个△ABC,再画一个△A'B'C',使A'B'=AB,∠A'=∠A,∠B'=∠B(即两角和它们的夹边对应相等). 学生先自己独立思考,动手画一画。在画的过程中若遇到不能解决的问题.可小组合作交流解决.2.把画好的△A'B'C'剪下,放到△ABC上,看看它们是否全等.画法:1、画A’B’=AB;2、在 A’B’的同旁画∠DA’B’ =∠A , ∠EB’A’ =∠B, A’D,B’E交于点C’。△A’B’C’就是所要画的三角形。通过实验你发现了什么规律?结论:两角和它们的夹边分别相等的两个三角形全等(可以简写成“角边角”或“ASA”).思考上面问题:能配一块与原来一样的三角形模具吗 如果可以,带哪块去合适 你能说明其中理由吗 并说说你选择的理由。利用“角边角”可知,带第③块去,可以配到一个与原来全等的三角形教具。 思考自议问题情境导入,使学生自然而然回忆之前学习过的内容,并对即将要学习的内容有一定的认识。 通过实际情境的分析,注重从一般到特殊,激发学生探究的兴趣,由此说明数学来源于生活。
讲授新课 提炼概念典例精讲例1、如图,D在AB上,E在AC上,AB=AC,∠B=∠C.求证:AD=AE. [分析]AD和AE分别在△ADC和△AEB中,所以要证AD=AE,只需证明△ADC≌△AEB即可. 证明:在△ADC和△AEB中 所以△ADC≌△AEB(ASA)所以AD=AE.探究2:在△ABC和△DEF中,∠A=∠D,∠B=∠E,BC=EF,△ABC与△DEF全等吗 能利用角边角条件证明你的结论吗 在△ABC和△DEF中,∠A +∠B +∠C=1800, ∠D +∠E +∠F =1800,∵ ∠A =∠D, ∠B=∠E, ∴ ∠C=∠F, 在ABC和DEF中∴ ∠B=∠E, BC=EF, ∠C=∠F, ∴ △ABC ≌△DEF (ASA)结论:两角和其中一个角的对边分别相等的两个三角形全等(可以简写成“角角边”或“AAS”).注意:这里的边是其中一角的对边,要注意区分!小结:现在为止,判定两个三角形全等我们已有了哪些方法 你能总结一下吗? 结论:SSS SAS ASA AAS(让学生自我总结、画图,然后教师在点评,一定要强调清楚SSA是不能判定全等的) 1、通过结合课前情景导入的内容,从与之相关的条件开始进行证明,学生自己动手,加深印象。2、学生动手,对两种条件进行比较,并回忆SAS的相关,进一步理解AAS与ASA。 通过动画演示全等变换的过程及学生动手实践,让学生形成直观感觉,从而分析总结出图形变换的本质,进一步加深对图形变换的理解,培养学生动态研究几何图形的意识。
课堂练习 四、巩固训练1. 如图,∠1=∠2,∠3=∠4,则判定△ABD和△ACD全等的依据是( )A. SSS B. ASA C. SAS D. AASB2. 在△ABC和△A′B′C′中,已知AB=A′B′,∠A=∠A′,∠C=∠C′,直接判定△ABC≌△A′B′C′的根据是 ( )A. SSS B. ASA C. AAS D. SASC3、如图,在下列条件中,不能直接证明△ABD≌△ACD的是( )A. BD=DC,AB=ACB. ∠ADB=∠ADC,BD=DCC. ∠B=∠C,∠BAD=∠CADD. ∠B=∠C,BD=DCD4.如图,∠B=∠DEF,AB=DE,要说明△ABC≌△DEF.(1)若以“SAS”为依据,还缺条件________________;(2)若以“ASA”为依据,还缺条件________________;(3)若以“AAS”为依据,还缺条件_____________________.(1)BC=EF (2)∠A=∠D (3)∠ACB=∠DFE5.如图,要测量池塘两岸相对的两点A,B的距离,可以在池塘外取AB的垂线BF上两点C,D,使BC=CD,再画出BF的垂线DE,使E与A,C在一条直线上,这时测得DE的长就是AB的长.为什么?解:∵ AB⊥BF,DE⊥BF, ∴ ∠ABC=∠EDC=90° ,在△ABC和△EDC中, ∴ △ABC≌△EDC (ASA) ,∴ AB=ED.6. 如图,已知∠D=∠E,AG=GD=CF=FE,A,B,C三点共线.求证:AB=CB.
课堂小结 课堂小结
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
