数学人教A版(2019)选择性必修第一册3.1.2椭圆的简单几何性质(共19张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册3.1.2椭圆的简单几何性质(共19张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-17 18:54:39 | ||
图片预览



文档简介
(共19张PPT)
3.1.2 椭圆的简单几何性质
学习目标
1.椭圆的定义:
平面内与两个定点、的距离之和为常数(大于)的动点的轨迹叫做椭圆.
2.椭圆的标准方程:
3.椭圆中的关系:
当焦点在x轴上时
当焦点在y轴上时
这两个定点叫做椭圆的焦点,两个焦点间的距离叫做椭圆的焦距。
复习回回顾
新知探索
l
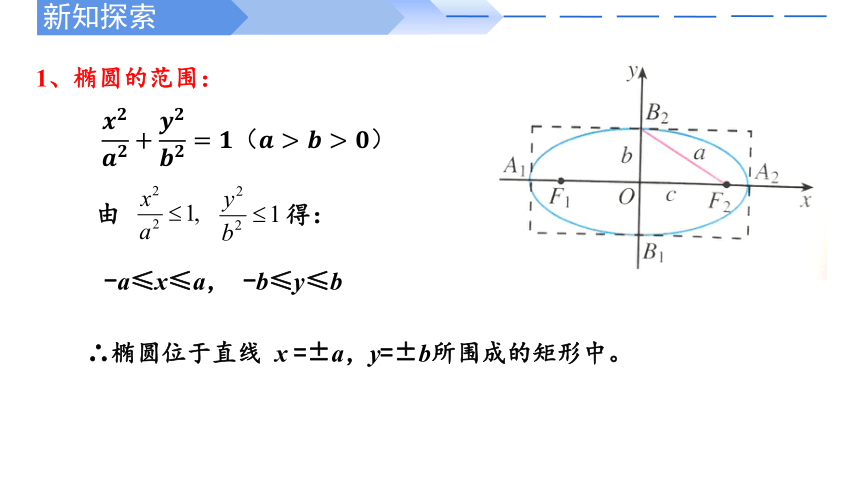
1、椭圆的范围:
由 得:
-a≤x≤a, -b≤y≤b
∴椭圆位于直线 x =±a,y=±b所围成的矩形中。
新知探索
l
l
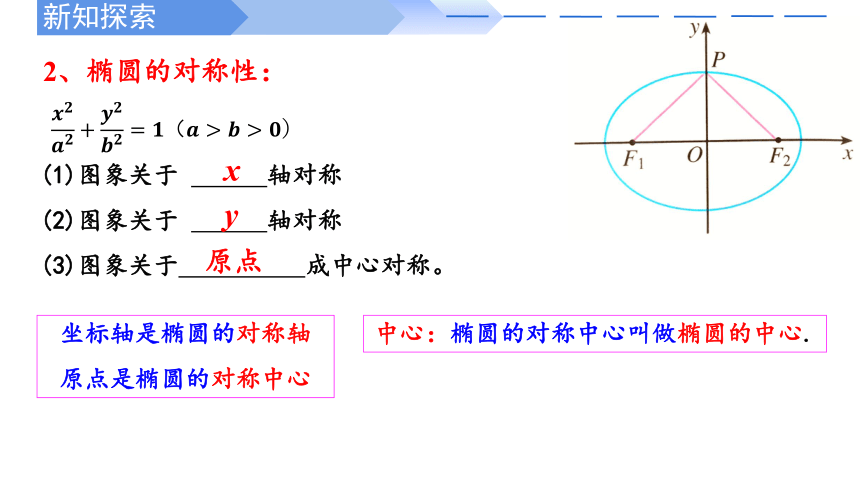
2、椭圆的对称性:
(1)图象关于 轴对称
(2)图象关于 轴对称
(3)图象关于 成中心对称。
y
x
原点
坐标轴是椭圆的对称轴
原点是椭圆的对称中心
中心:椭圆的对称中心叫做椭圆的中心.
新知探索
3、椭圆的顶点:
顶点:椭圆与它的对称轴的四个交点,叫做椭圆的顶点。
椭圆顶点坐标:
长轴:线段A1A2 长轴长:|A1A2|=2a 长半轴长:a
短轴:线段B1B2 短轴长:|B1B2|=2b 短半轴长:b
新知探索
l
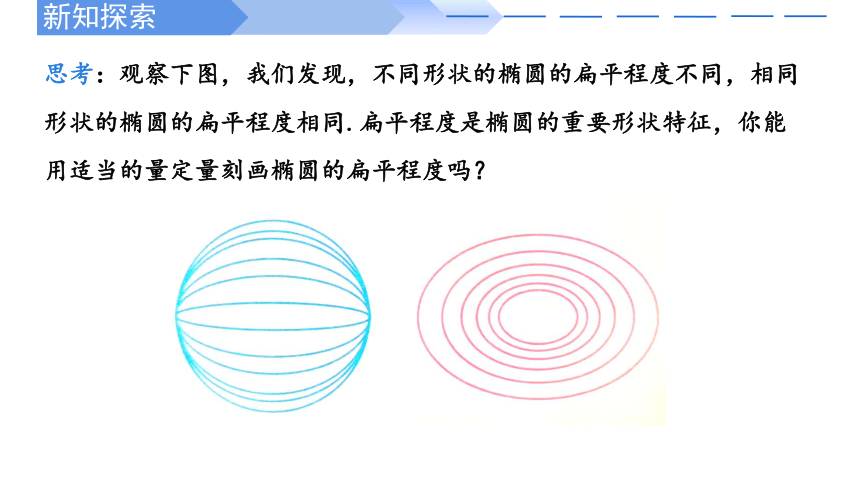
思考:观察下图,我们发现,不同形状的椭圆的扁平程度不同,相同形状的椭圆的扁平程度相同.扁平程度是椭圆的重要形状特征,你能用适当的量定量刻画椭圆的扁平程度吗?
l
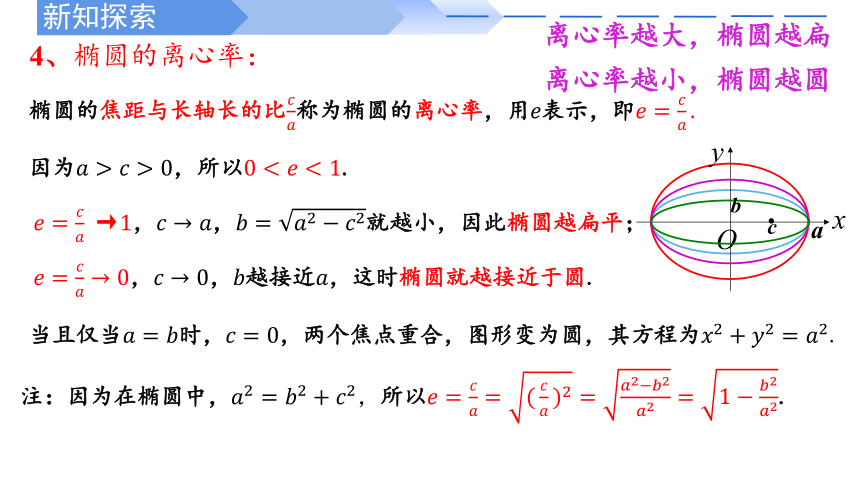
注:因为在椭圆中,,所以.
4、椭圆的离心率:
离心率越大,椭圆越扁
离心率越小,椭圆越圆
O
x
y
a
b
●
c
椭圆的焦距与长轴长的比称为椭圆的离心率,用表示,即
因为,所以.
→,,就越小,因此椭圆越扁平;
,,越接近,这时椭圆就越接近于圆.
当且仅当时,,两个焦点重合,图形变为圆,其方程为.
新知探索
新知探索
椭圆的简单几何性质
新知探索
辨析:判断正误.
(1)椭圆的长轴长等于.( )
(2)椭圆上的点到焦点的距离的最小值为,最大值为.( )
(3)椭圆的离心率越小,椭圆越圆.( )
(4)若一个矩形的四个顶点都在椭圆上,则这四个顶点关于椭圆的中心对称.( )
×
√
√
√
例题
题型一:由椭圆的标准方程研究其几何性质用
例1.求椭圆的长轴长、短轴长、离心率、焦点和顶点坐标,并画出图形。
椭圆的长轴长,短轴长,离心率,
两个焦点坐标分别是和,
四个顶点坐标分别是,,和.
解:把原方程化为标准方程为,
于是,
练习
变式:已知椭圆,设椭圆与椭圆的长轴长、短轴长分别相等,且椭圆的焦点在轴上.求椭圆的长半轴长、短半轴长、焦点坐标及离心率;
解:由椭圆可得,
其长半轴长为10,短半轴长为8,
焦点坐标为,,
离心率.
例题
题型二:利用几何性质求椭圆的标准方程
例2.求适合下列条件的椭圆的标准方程.
(1)长轴长是10,离心率是;
解(1):设椭圆方程为或.
由已知得,.
又∵,∴.
∴.
∴椭圆方程为或.
(2)在轴上的一个焦点与短轴两个端点的连线互相垂直,且焦距为6.
例题
(2)在轴上的一个焦点与短轴两个端点的连线互相垂直,且焦距为6.
解(2):依题意可设椭圆方程为.
如图所示,为等腰直角三角形,
,,
则,,
故所求椭圆的方程为.
B2
B1
练习
方法技巧:利用性质求椭圆方程的方法和步骤
1.方法:利用椭圆的几何性质求标准方程,通常采用待定系数法.
2.步骤:(1)确定焦点位置;
(2)根据已知条件构造关于参数的关系式,利用方程(组)求得参数.
练习:课本112页练习题3、4
练习
题型三:椭圆离心率的求法及应用
例3.(2018年全卷Ⅱ)已知,是椭圆的两个焦点,是上的一点.若,且,则的离心率为( ).
A. B. C. D.
D
练习
变式:如图,设椭圆的左、右焦点分别为F1,F2,过F1作椭圆长轴的垂线交椭圆于点P,若△F1PF2为等腰直角三角形,求椭圆的离心率.
椭圆的通径:过焦点垂直于长轴的直线与椭圆相交所得的线段长度,椭圆的通径长为
练习
方法技巧:求椭圆离心率的值或范围的两种方法
1.直接法:由题目条件直接求出,再代入公式求解.
2.方程法:若的值不可求,则可根据条件建立的关系式,借助,转化为关于的齐次方程或不等式,再将方程或不等式两边同时除以的最高次幂,得到关于的方程或不等式,即可求得的值或范围.
椭圆的简单几何性质
课堂小结
课堂小结
离心率的性质:
(1)越接近,越接近,就越小,因此椭圆越扁平;
(2)越接近,越接近,越接近,这时椭圆就越接近于圆;
(3)当且仅当时,,这时两个焦点重合,图形变为圆.
3.1.2 椭圆的简单几何性质
学习目标
1.椭圆的定义:
平面内与两个定点、的距离之和为常数(大于)的动点的轨迹叫做椭圆.
2.椭圆的标准方程:
3.椭圆中的关系:
当焦点在x轴上时
当焦点在y轴上时
这两个定点叫做椭圆的焦点,两个焦点间的距离叫做椭圆的焦距。
复习回回顾
新知探索
l
1、椭圆的范围:
由 得:
-a≤x≤a, -b≤y≤b
∴椭圆位于直线 x =±a,y=±b所围成的矩形中。
新知探索
l
l
2、椭圆的对称性:
(1)图象关于 轴对称
(2)图象关于 轴对称
(3)图象关于 成中心对称。
y
x
原点
坐标轴是椭圆的对称轴
原点是椭圆的对称中心
中心:椭圆的对称中心叫做椭圆的中心.
新知探索
3、椭圆的顶点:
顶点:椭圆与它的对称轴的四个交点,叫做椭圆的顶点。
椭圆顶点坐标:
长轴:线段A1A2 长轴长:|A1A2|=2a 长半轴长:a
短轴:线段B1B2 短轴长:|B1B2|=2b 短半轴长:b
新知探索
l
思考:观察下图,我们发现,不同形状的椭圆的扁平程度不同,相同形状的椭圆的扁平程度相同.扁平程度是椭圆的重要形状特征,你能用适当的量定量刻画椭圆的扁平程度吗?
l
注:因为在椭圆中,,所以.
4、椭圆的离心率:
离心率越大,椭圆越扁
离心率越小,椭圆越圆
O
x
y
a
b
●
c
椭圆的焦距与长轴长的比称为椭圆的离心率,用表示,即
因为,所以.
→,,就越小,因此椭圆越扁平;
,,越接近,这时椭圆就越接近于圆.
当且仅当时,,两个焦点重合,图形变为圆,其方程为.
新知探索
新知探索
椭圆的简单几何性质
新知探索
辨析:判断正误.
(1)椭圆的长轴长等于.( )
(2)椭圆上的点到焦点的距离的最小值为,最大值为.( )
(3)椭圆的离心率越小,椭圆越圆.( )
(4)若一个矩形的四个顶点都在椭圆上,则这四个顶点关于椭圆的中心对称.( )
×
√
√
√
例题
题型一:由椭圆的标准方程研究其几何性质用
例1.求椭圆的长轴长、短轴长、离心率、焦点和顶点坐标,并画出图形。
椭圆的长轴长,短轴长,离心率,
两个焦点坐标分别是和,
四个顶点坐标分别是,,和.
解:把原方程化为标准方程为,
于是,
练习
变式:已知椭圆,设椭圆与椭圆的长轴长、短轴长分别相等,且椭圆的焦点在轴上.求椭圆的长半轴长、短半轴长、焦点坐标及离心率;
解:由椭圆可得,
其长半轴长为10,短半轴长为8,
焦点坐标为,,
离心率.
例题
题型二:利用几何性质求椭圆的标准方程
例2.求适合下列条件的椭圆的标准方程.
(1)长轴长是10,离心率是;
解(1):设椭圆方程为或.
由已知得,.
又∵,∴.
∴.
∴椭圆方程为或.
(2)在轴上的一个焦点与短轴两个端点的连线互相垂直,且焦距为6.
例题
(2)在轴上的一个焦点与短轴两个端点的连线互相垂直,且焦距为6.
解(2):依题意可设椭圆方程为.
如图所示,为等腰直角三角形,
,,
则,,
故所求椭圆的方程为.
B2
B1
练习
方法技巧:利用性质求椭圆方程的方法和步骤
1.方法:利用椭圆的几何性质求标准方程,通常采用待定系数法.
2.步骤:(1)确定焦点位置;
(2)根据已知条件构造关于参数的关系式,利用方程(组)求得参数.
练习:课本112页练习题3、4
练习
题型三:椭圆离心率的求法及应用
例3.(2018年全卷Ⅱ)已知,是椭圆的两个焦点,是上的一点.若,且,则的离心率为( ).
A. B. C. D.
D
练习
变式:如图,设椭圆的左、右焦点分别为F1,F2,过F1作椭圆长轴的垂线交椭圆于点P,若△F1PF2为等腰直角三角形,求椭圆的离心率.
椭圆的通径:过焦点垂直于长轴的直线与椭圆相交所得的线段长度,椭圆的通径长为
练习
方法技巧:求椭圆离心率的值或范围的两种方法
1.直接法:由题目条件直接求出,再代入公式求解.
2.方程法:若的值不可求,则可根据条件建立的关系式,借助,转化为关于的齐次方程或不等式,再将方程或不等式两边同时除以的最高次幂,得到关于的方程或不等式,即可求得的值或范围.
椭圆的简单几何性质
课堂小结
课堂小结
离心率的性质:
(1)越接近,越接近,就越小,因此椭圆越扁平;
(2)越接近,越接近,越接近,这时椭圆就越接近于圆;
(3)当且仅当时,,这时两个焦点重合,图形变为圆.
