沪科版八年级数学上册 第11章 平面直角坐标系(点的坐标变化规律与新定义问题) 一课一练(含答案)
文档属性
| 名称 | 沪科版八年级数学上册 第11章 平面直角坐标系(点的坐标变化规律与新定义问题) 一课一练(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 145.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-17 07:20:21 | ||
图片预览



文档简介
《平面直角坐标系--点的坐标变化规律与新定义问题》
一、选择题.
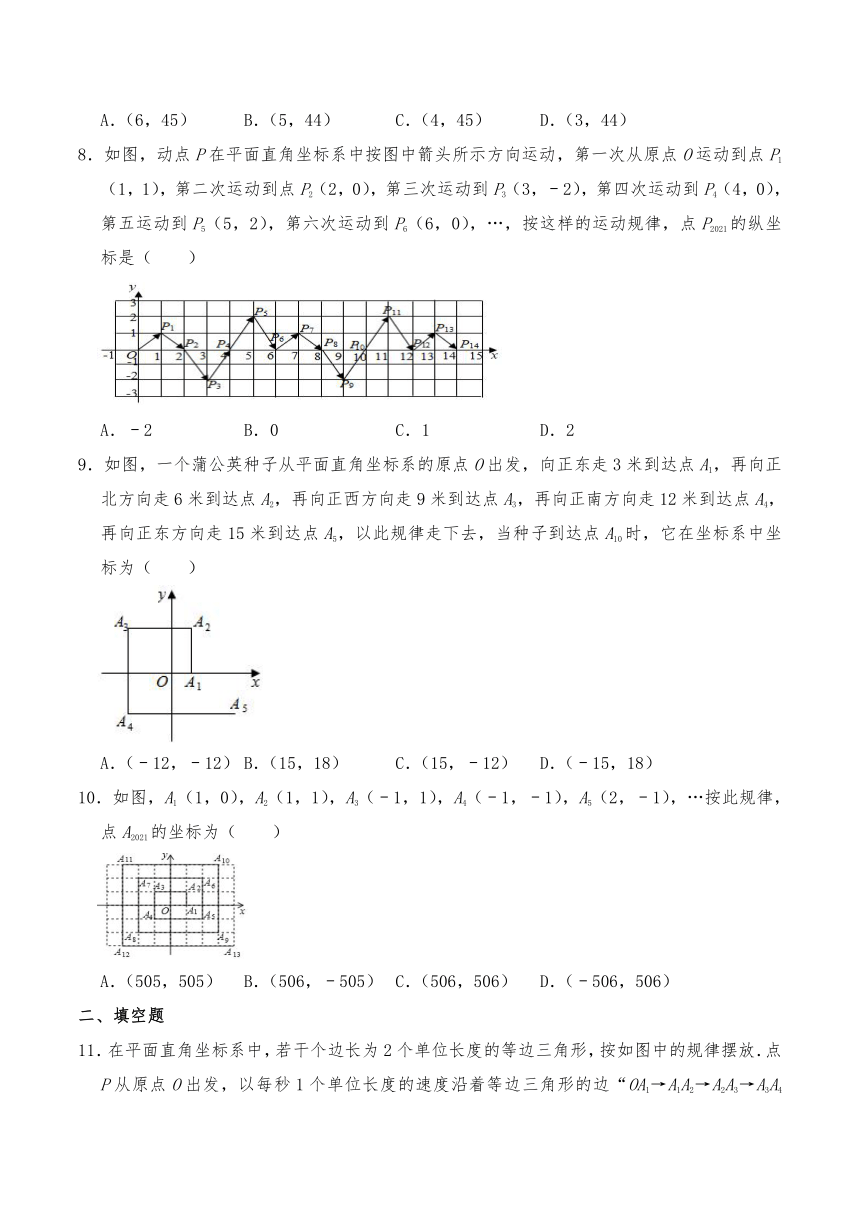
1.如图,点A(0,1),点A1(2,0),点A2(3,2),点A3(5,1)…,按照这样的规律下去,点A100的坐标为( )
A.(101,100) B.(150,51) C.(150,50) D.(100,55)
2.如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第一次从原点O运动到点P1(1,1),第二次运动到点P2(2,0),第三次运动到P3(3,﹣2),…,按这样的运动规律,第2021次运动后,动点P2021的纵坐标是( )
A.1 B.2 C.﹣2 D.0
3.如图所示,在平面直角坐标系中,半径均为1个单位长度的半圆O1,O2,O3,…组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒个单位长度,则第2020秒时,点P的坐标是( )
A.(2019,0) B.(2020,0) C.(2019,1) D.(2020,﹣1)
4.如图,在平面直角坐标系中,从点P1(﹣2,0),P2(﹣2,﹣2),P3(2,﹣2),P4(2,2),P5(﹣4,2),P6(﹣4,﹣4),P7(4,﹣4),P8(4,4),P9(﹣6,4),…,依此扩展下去,则P2019的坐标为( )
A.(1010,﹣1010) B.(﹣1010,﹣1010)
C.(1010,1010) D.(﹣1012,1010)
5.在平面直角坐标系xOy中,对于点P(x,y),我们把P1(y﹣1,﹣x﹣1)叫做点P的友好点,已知点A1的友好点为A2,点A2的友好点为A3,点A3的友好点为A4,这样依次得到各点.若A2021的坐标为(﹣3,2),设A1(x,y),则x+y的值是( )
A.﹣5 B.3 C.﹣1 D.5
6.在平面直角坐标系中,点A(1,0)第一次向左跳动至A1(﹣1,1),第二次向右跳至A2(2,1),第三次向左跳至A3(﹣2,2),第四次向右跳至A4(3,2),…,按照此规律,点A第2021次跳动至A2021的坐标是( )
A.(﹣1011,1011) B.(1011,1010)
C.(﹣1010,1010) D.(1010,1009)
7.一只青蛙在第一象限及x、y轴上跳动,第一次它从原点跳到(0,1),然后按图中箭头所示方向跳动(0,0)→(0,1)→(1,1)→(1,0)→……,每次跳一个单位长度,则第2021次跳到点( )
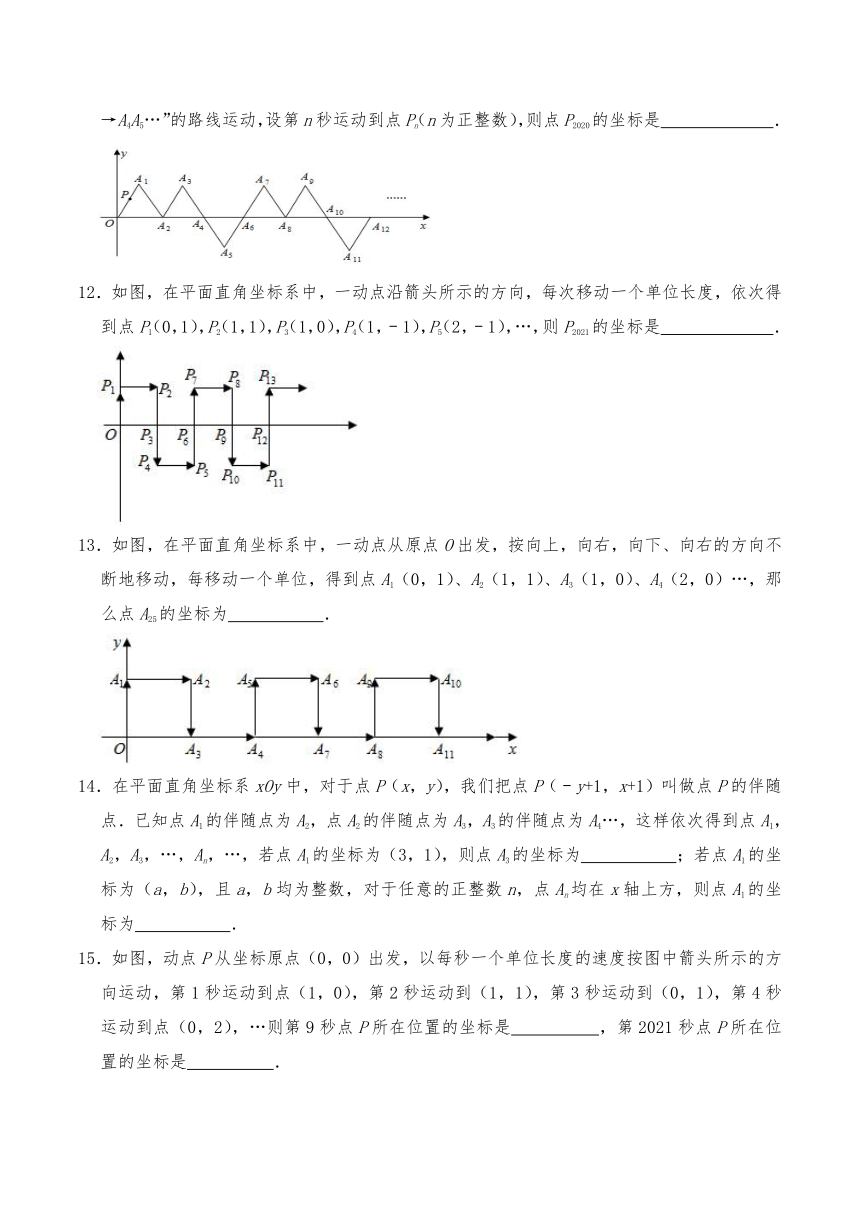
A.(6,45) B.(5,44) C.(4,45) D.(3,44)
8.如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第一次从原点O运动到点P1(1,1),第二次运动到点P2(2,0),第三次运动到P3(3,﹣2),第四次运动到P4(4,0),第五运动到P5(5,2),第六次运动到P6(6,0),…,按这样的运动规律,点P2021的纵坐标是( )
A.﹣2 B.0 C.1 D.2
9.如图,一个蒲公英种子从平面直角坐标系的原点O出发,向正东走3米到达点A1,再向正北方向走6米到达点A2,再向正西方向走9米到达点A3,再向正南方向走12米到达点A4,再向正东方向走15米到达点A5,以此规律走下去,当种子到达点A10时,它在坐标系中坐标为( )
A.(﹣12,﹣12) B.(15,18) C.(15,﹣12) D.(﹣15,18)
10.如图,A1(1,0),A2(1,1),A3(﹣1,1),A4(﹣1,﹣1),A5(2,﹣1),…按此规律,点A2021的坐标为( )
A.(505,505) B.(506,﹣505) C.(506,506) D.(﹣506,506)
二、填空题
11.在平面直角坐标系中,若干个边长为2个单位长度的等边三角形,按如图中的规律摆放.点P从原点O出发,以每秒1个单位长度的速度沿着等边三角形的边“OA1→A1A2→A2A3→A3A4→A4A5…”的路线运动,设第n秒运动到点Pn(n为正整数),则点P2020的坐标是 .
12.如图,在平面直角坐标系中,一动点沿箭头所示的方向,每次移动一个单位长度,依次得到点P1(0,1),P2(1,1),P3(1,0),P4(1,﹣1),P5(2,﹣1),…,则P2021的坐标是 .
13.如图,在平面直角坐标系中,一动点从原点O出发,按向上,向右,向下、向右的方向不断地移动,每移动一个单位,得到点A1(0,1)、A2(1,1)、A3(1,0)、A4(2,0)…,那么点A25的坐标为 .
14.在平面直角坐标系xOy中,对于点P(x,y),我们把点P(﹣y+1,x+1)叫做点P的伴随点.已知点A1的伴随点为A2,点A2的伴随点为A3,A3的伴随点为A4…,这样依次得到点A1,A2,A3,…,An,…,若点A1的坐标为(3,1),则点A3的坐标为 ;若点A1的坐标为(a,b),且a,b均为整数,对于任意的正整数n,点An均在x轴上方,则点A1的坐标为 .
15.如图,动点P从坐标原点(0,0)出发,以每秒一个单位长度的速度按图中箭头所示的方向运动,第1秒运动到点(1,0),第2秒运动到(1,1),第3秒运动到(0,1),第4秒运动到点(0,2),…则第9秒点P所在位置的坐标是 ,第2021秒点P所在位置的坐标是 .
16.在平面直角坐标系xOy中,对于点P(x,y)我们把P′(﹣y+1,x+1)叫做点P的伴随点,已知A1的伴随点为A2,点A2的伴随点为A3,点A3的伴随点为A4,这样依次得到A1,A2,A3,…An,若点A1的坐标为(3,1),则点A2017的坐标为 .
17.如图,动点P从(0,3)出发,沿所示方向运动,每当碰到长方形OABC的边时反弹,反弹时反射角等于入射角,当点P第2020次碰到长方形OABC的边时,点P的坐标为 .
18.在直角坐标系中,下面各点按顺序依次排列:(1,0),(0,1),(1,1),(﹣2,0),(0,﹣2),(﹣2,﹣2),(3,0),(0,3),(3,3),(﹣4,0),(0,﹣4),(﹣4,﹣4)…,按此规律,这列点中第1000个点的坐标是 .
三、解答题
19.已知当m,n都是实数.且满足2m=8+n时,称p(m﹣1,)为“开心点”.
(1)判断点A(5,3),B(4,10)是否为“开心点”,并说明理由;
(2)若点M(a,2a﹣1)是“开心点”,请判断点M在第几象限?并说明理由.
20.在平面直角坐标系中,一只蜗牛从原点O出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位长度,其行走路线如图所示:
(1)填写下列各点的坐标:A5( , ),A9( , ),A13( , );
(2)写出点A4n+1的坐标(n是正整数);
(3)指出蜗牛从点A2020到点A2021的移动方向.
21.如图,在平面直角坐标系中,一动点从原点O出发,沿着箭头所示方向,每次移动1个单位,依次得到点P1(0,1),P2(1,1),P3(1,0),P4(1,﹣1),P5(2,﹣1),P6(2,0)…
(1)填写下列各点的坐标:P9( ),P12( 、 ),P15( 、 )
(2)写出点P3n的坐标(n是正整数);
(3)点P60的坐标是( 、 );
(4)指出动点从点P210到点P211的移动方向.
22.已知整点P0在平面直角坐标系内做“跳马运动”(也就是中国象棋式“日字”型跳跃).例如,在下图中,从点A做一次“跳马运动”可以到点B,但是到不了点C.
设P0做一次跳马运动到点P1,再做一次跳马运动到点P2,再做一次跳马运动到点P3,……,如此继续下去
(1)若P(1,0),则P1可能是下列哪些点 ;
D(﹣1,2);E(﹣1,﹣1);F(﹣2,0);
(2)已知点P0(9,3),P2(5,3),则点P1的坐标为 ;
(3)P0为平面上一个定点,则点P7、P26可能与P0重合的是 ;
(4)P0为平面上一个定点,则线段P0P7长的最小值是 ;
(5)现在P0(1,0),规定每一次只向x轴的正方向跳跃,若P21(38,10),则P1,P2,……,P20点的纵坐标的最大值为 .
23.在平面直角坐标系xOy中,对于点P(x,y),我们把点P'(﹣y+1,x+1)叫做点P的伴随点.已知点A1的伴随点为A2,点A2的伴随点为A3,A3的伴随点为A4…,这样依次得到点A1,A2,A3,…,An,…
(1)若点A1的坐标为(3,1),则点A3的坐标为 ,点A2018的坐标为 ;
(2)若点A1的坐标为(a,b),对于任意的正整数n,点An均在x轴上方,则a,b应满足什么条件?
24.我们规定:在平面直角坐标系xOy中,任意不重合的两点M(x1,y1),N(x2,y2)之间的“折线距离”为d(M,N)=|x1﹣x2|+|y1﹣y2|.例如图1中,点M(﹣2,3)与点N(1,﹣1)之间的“折线距离”为d(M,N)=|﹣2﹣1|+|3﹣(﹣1)|=3+4=7.
根据上述知识,解决下面问题:
(1)已知点P(3,﹣4),在点A(5,2),B(﹣1,0),C(﹣2,1),D(0,1)中,与点P之间的“折线距离”为8的点是 ;
(2)如图2,已知点P(3,﹣4),若点Q的坐标为(t,2),且d(P,Q)=10,求t的值;
(3)如图2,已知点P(3,﹣4),若点Q的坐标为(t,t+1),且d(P,Q)=8,直接写出t的取值范围.
答案
一、选择题
B.B.B.A.C.A.D.D.B.B.
二、填空题
11.(1010,0).
12.(674,﹣1).
13.(12,1).
14.(0,1).
15.(2,1),(44,3).
16.(3,1).
17.(5,0).
18.(﹣334,0).
三、解答题
19.(1)点A(5,3)为“开心点”,理由如下,
当A(5,3)时,m﹣1=5,,得m=6,n=4,
则2m=12,8+n=12,
所以2m=8+n,
所以A(5,3)是“开心点”;
点B(4,10)不是“开心点”,理由如下,
当B(4,10)时,m﹣1=4,,得m=5,n=18,
则2m=10,8+18=26,
所以2m≠8+n,
所以点B(4,10)不是“开心点”;
(2)点M在第三象限,
理由如下:
∵点M(a,2a﹣1)是“开心点”,
∴m﹣1=a,,
∴m=a+1,n=4a﹣4,
代入2m=8+n有2a+2=8+4a﹣4,
∴a=﹣1,2a﹣1=﹣3,
∴M(﹣1,﹣3),
故点M在第三象限.
20.(1)根据点的坐标变化可知:
各点的坐标为:A5(2,1),A9(4,1),A13(6,1);
故答案为:2,1,4,1,6,1;
(2)根据(1)发现:
点A4n+1的坐标(n为正整数)为(2n,1);
(3)因为每四个点一个循环,
所以2021÷4=505…1.
所以蜗牛从点A2020到点A2021的移动方向是向上.
21.(1)由动点运动方向与长度可得P3(1,0),P6(2,0),
可以发现脚标是3的倍数的点,依次排列在x轴上,且相距1个单位,
即动点运动三次与横轴相交,
故答案为P9( 3,0),P12(4、0 ),P15(5、0 ).
(2)由(1)可归纳总结点P3n的坐标为P3n(n,0),(n是正整数);
(3)根据(2),∵60=3×20,∴点P60的横坐标是20
故点P60的坐标是(20、0 )
故答案为(20、0 ).
(4)∵210=3×70,符合(2)中的规律
∴点P210在x轴上,
又由图象规律可以发现当动点在x 轴上时,偶数点向上运动,奇数点向下运动,
而点P210是在x轴上的偶数点
所以动点从点P210到点P211的移动方向应该是向上.
22.(1)由题意,知跳马运动一次,则有2种情况,一种为横坐标变化2个单位,纵坐标变化1个单位;另一种为横坐标变化1个单位,纵坐标变化2个单位,
∴P1可能为E(﹣1,﹣1);
(2)P0至P2经两次运动,横坐标变小4个单位,纵坐标不变,则P1可能为P1(7,2)或P1(7,4);
故答案为:P1(7,2)或P1(7,4);
(3)P0为平面上一个定点,则点P7、P26可能与P0重合的是P26;
故答案为:P26;
(4)∵P0在平面直角坐标系内做“跳马运动”,即P0与P2、P4、P6重合,
∴P0P7长的最小值是:.
故答案为:;
(5)从P0至P21共21次变化,每次都向x轴正向运动,则横坐标始终变大,设有x次运动,为横坐标变化2个单位,纵坐标变一个单位,则有(21﹣x)次为纵坐标变化2个单位,横坐标变1个单位,
∴2x+21﹣x=38﹣1,
∴x=16,
设有m次为纵坐标变大1个单位,则有(16﹣m)次变小1单位,有n次纵坐标变大2单位,(5﹣n)次变小2单位,
m+2n﹣(16﹣m)﹣2(5﹣n)=10,
∴m=18﹣2n,
∴纵坐标最大为:m+2n=18.
故答案为:18.
23.(1)∵A1的坐标为(3,1),
∴A2(0,4),A3(﹣3,1),A4(0,﹣2),A5(3,1),
…,
依此类推,每4个点为一个循环组依次循环,
∵2018÷4=504余2,
∴点A2018的坐标与A2的坐标相同,为(0,4);
故答案为:(﹣3,1),(0,4);
(2)∵点A1的坐标为(a,b),
∴A2(﹣b+1,a+1),A3(﹣a,﹣b+2),A4(b﹣1,﹣a+1),A5(a,b),
…,
依此类推,每4个点为一个循环组依次循环,
∵对于任意的正整数n,点An均在x轴上方,
∴,,
解得﹣1<a<1,0<b<2.
24.(1)由题意得d(P,A)=|3﹣5|+|﹣4﹣2|=8,
d(P,B)=|3﹣(﹣1)|+|﹣4﹣0|=8,
d(P,C)=|3﹣(﹣2)|+|﹣4﹣1|=10,
d(P,D)=|3﹣0|+|﹣4﹣1|=8,
故答案为:A,B,D.
(2)d(P,Q)=|3﹣t|+|﹣4﹣2|=10,
解得t=﹣1或t=7.
(3)d(P,Q)=|3﹣t|+|﹣4﹣(t+1)|,
化简得d(P,Q)=|3﹣t|+|5+t|,
当﹣5≤t≤3时,|3﹣t|+|5+t|=3﹣t+5+t=8,满足题意.
当t<﹣5时,|3﹣t|+|5+t|=3﹣t﹣5﹣t=﹣2﹣2t,不满足题意.
当t>3时,|3﹣t|+|5+t|=t﹣3+5+t=2+2t,不满足题意.
∴﹣5≤t≤3.
一、选择题.
1.如图,点A(0,1),点A1(2,0),点A2(3,2),点A3(5,1)…,按照这样的规律下去,点A100的坐标为( )
A.(101,100) B.(150,51) C.(150,50) D.(100,55)
2.如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第一次从原点O运动到点P1(1,1),第二次运动到点P2(2,0),第三次运动到P3(3,﹣2),…,按这样的运动规律,第2021次运动后,动点P2021的纵坐标是( )
A.1 B.2 C.﹣2 D.0
3.如图所示,在平面直角坐标系中,半径均为1个单位长度的半圆O1,O2,O3,…组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒个单位长度,则第2020秒时,点P的坐标是( )
A.(2019,0) B.(2020,0) C.(2019,1) D.(2020,﹣1)
4.如图,在平面直角坐标系中,从点P1(﹣2,0),P2(﹣2,﹣2),P3(2,﹣2),P4(2,2),P5(﹣4,2),P6(﹣4,﹣4),P7(4,﹣4),P8(4,4),P9(﹣6,4),…,依此扩展下去,则P2019的坐标为( )
A.(1010,﹣1010) B.(﹣1010,﹣1010)
C.(1010,1010) D.(﹣1012,1010)
5.在平面直角坐标系xOy中,对于点P(x,y),我们把P1(y﹣1,﹣x﹣1)叫做点P的友好点,已知点A1的友好点为A2,点A2的友好点为A3,点A3的友好点为A4,这样依次得到各点.若A2021的坐标为(﹣3,2),设A1(x,y),则x+y的值是( )
A.﹣5 B.3 C.﹣1 D.5
6.在平面直角坐标系中,点A(1,0)第一次向左跳动至A1(﹣1,1),第二次向右跳至A2(2,1),第三次向左跳至A3(﹣2,2),第四次向右跳至A4(3,2),…,按照此规律,点A第2021次跳动至A2021的坐标是( )
A.(﹣1011,1011) B.(1011,1010)
C.(﹣1010,1010) D.(1010,1009)
7.一只青蛙在第一象限及x、y轴上跳动,第一次它从原点跳到(0,1),然后按图中箭头所示方向跳动(0,0)→(0,1)→(1,1)→(1,0)→……,每次跳一个单位长度,则第2021次跳到点( )
A.(6,45) B.(5,44) C.(4,45) D.(3,44)
8.如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第一次从原点O运动到点P1(1,1),第二次运动到点P2(2,0),第三次运动到P3(3,﹣2),第四次运动到P4(4,0),第五运动到P5(5,2),第六次运动到P6(6,0),…,按这样的运动规律,点P2021的纵坐标是( )
A.﹣2 B.0 C.1 D.2
9.如图,一个蒲公英种子从平面直角坐标系的原点O出发,向正东走3米到达点A1,再向正北方向走6米到达点A2,再向正西方向走9米到达点A3,再向正南方向走12米到达点A4,再向正东方向走15米到达点A5,以此规律走下去,当种子到达点A10时,它在坐标系中坐标为( )
A.(﹣12,﹣12) B.(15,18) C.(15,﹣12) D.(﹣15,18)
10.如图,A1(1,0),A2(1,1),A3(﹣1,1),A4(﹣1,﹣1),A5(2,﹣1),…按此规律,点A2021的坐标为( )
A.(505,505) B.(506,﹣505) C.(506,506) D.(﹣506,506)
二、填空题
11.在平面直角坐标系中,若干个边长为2个单位长度的等边三角形,按如图中的规律摆放.点P从原点O出发,以每秒1个单位长度的速度沿着等边三角形的边“OA1→A1A2→A2A3→A3A4→A4A5…”的路线运动,设第n秒运动到点Pn(n为正整数),则点P2020的坐标是 .
12.如图,在平面直角坐标系中,一动点沿箭头所示的方向,每次移动一个单位长度,依次得到点P1(0,1),P2(1,1),P3(1,0),P4(1,﹣1),P5(2,﹣1),…,则P2021的坐标是 .
13.如图,在平面直角坐标系中,一动点从原点O出发,按向上,向右,向下、向右的方向不断地移动,每移动一个单位,得到点A1(0,1)、A2(1,1)、A3(1,0)、A4(2,0)…,那么点A25的坐标为 .
14.在平面直角坐标系xOy中,对于点P(x,y),我们把点P(﹣y+1,x+1)叫做点P的伴随点.已知点A1的伴随点为A2,点A2的伴随点为A3,A3的伴随点为A4…,这样依次得到点A1,A2,A3,…,An,…,若点A1的坐标为(3,1),则点A3的坐标为 ;若点A1的坐标为(a,b),且a,b均为整数,对于任意的正整数n,点An均在x轴上方,则点A1的坐标为 .
15.如图,动点P从坐标原点(0,0)出发,以每秒一个单位长度的速度按图中箭头所示的方向运动,第1秒运动到点(1,0),第2秒运动到(1,1),第3秒运动到(0,1),第4秒运动到点(0,2),…则第9秒点P所在位置的坐标是 ,第2021秒点P所在位置的坐标是 .
16.在平面直角坐标系xOy中,对于点P(x,y)我们把P′(﹣y+1,x+1)叫做点P的伴随点,已知A1的伴随点为A2,点A2的伴随点为A3,点A3的伴随点为A4,这样依次得到A1,A2,A3,…An,若点A1的坐标为(3,1),则点A2017的坐标为 .
17.如图,动点P从(0,3)出发,沿所示方向运动,每当碰到长方形OABC的边时反弹,反弹时反射角等于入射角,当点P第2020次碰到长方形OABC的边时,点P的坐标为 .
18.在直角坐标系中,下面各点按顺序依次排列:(1,0),(0,1),(1,1),(﹣2,0),(0,﹣2),(﹣2,﹣2),(3,0),(0,3),(3,3),(﹣4,0),(0,﹣4),(﹣4,﹣4)…,按此规律,这列点中第1000个点的坐标是 .
三、解答题
19.已知当m,n都是实数.且满足2m=8+n时,称p(m﹣1,)为“开心点”.
(1)判断点A(5,3),B(4,10)是否为“开心点”,并说明理由;
(2)若点M(a,2a﹣1)是“开心点”,请判断点M在第几象限?并说明理由.
20.在平面直角坐标系中,一只蜗牛从原点O出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位长度,其行走路线如图所示:
(1)填写下列各点的坐标:A5( , ),A9( , ),A13( , );
(2)写出点A4n+1的坐标(n是正整数);
(3)指出蜗牛从点A2020到点A2021的移动方向.
21.如图,在平面直角坐标系中,一动点从原点O出发,沿着箭头所示方向,每次移动1个单位,依次得到点P1(0,1),P2(1,1),P3(1,0),P4(1,﹣1),P5(2,﹣1),P6(2,0)…
(1)填写下列各点的坐标:P9( ),P12( 、 ),P15( 、 )
(2)写出点P3n的坐标(n是正整数);
(3)点P60的坐标是( 、 );
(4)指出动点从点P210到点P211的移动方向.
22.已知整点P0在平面直角坐标系内做“跳马运动”(也就是中国象棋式“日字”型跳跃).例如,在下图中,从点A做一次“跳马运动”可以到点B,但是到不了点C.
设P0做一次跳马运动到点P1,再做一次跳马运动到点P2,再做一次跳马运动到点P3,……,如此继续下去
(1)若P(1,0),则P1可能是下列哪些点 ;
D(﹣1,2);E(﹣1,﹣1);F(﹣2,0);
(2)已知点P0(9,3),P2(5,3),则点P1的坐标为 ;
(3)P0为平面上一个定点,则点P7、P26可能与P0重合的是 ;
(4)P0为平面上一个定点,则线段P0P7长的最小值是 ;
(5)现在P0(1,0),规定每一次只向x轴的正方向跳跃,若P21(38,10),则P1,P2,……,P20点的纵坐标的最大值为 .
23.在平面直角坐标系xOy中,对于点P(x,y),我们把点P'(﹣y+1,x+1)叫做点P的伴随点.已知点A1的伴随点为A2,点A2的伴随点为A3,A3的伴随点为A4…,这样依次得到点A1,A2,A3,…,An,…
(1)若点A1的坐标为(3,1),则点A3的坐标为 ,点A2018的坐标为 ;
(2)若点A1的坐标为(a,b),对于任意的正整数n,点An均在x轴上方,则a,b应满足什么条件?
24.我们规定:在平面直角坐标系xOy中,任意不重合的两点M(x1,y1),N(x2,y2)之间的“折线距离”为d(M,N)=|x1﹣x2|+|y1﹣y2|.例如图1中,点M(﹣2,3)与点N(1,﹣1)之间的“折线距离”为d(M,N)=|﹣2﹣1|+|3﹣(﹣1)|=3+4=7.
根据上述知识,解决下面问题:
(1)已知点P(3,﹣4),在点A(5,2),B(﹣1,0),C(﹣2,1),D(0,1)中,与点P之间的“折线距离”为8的点是 ;
(2)如图2,已知点P(3,﹣4),若点Q的坐标为(t,2),且d(P,Q)=10,求t的值;
(3)如图2,已知点P(3,﹣4),若点Q的坐标为(t,t+1),且d(P,Q)=8,直接写出t的取值范围.
答案
一、选择题
B.B.B.A.C.A.D.D.B.B.
二、填空题
11.(1010,0).
12.(674,﹣1).
13.(12,1).
14.(0,1).
15.(2,1),(44,3).
16.(3,1).
17.(5,0).
18.(﹣334,0).
三、解答题
19.(1)点A(5,3)为“开心点”,理由如下,
当A(5,3)时,m﹣1=5,,得m=6,n=4,
则2m=12,8+n=12,
所以2m=8+n,
所以A(5,3)是“开心点”;
点B(4,10)不是“开心点”,理由如下,
当B(4,10)时,m﹣1=4,,得m=5,n=18,
则2m=10,8+18=26,
所以2m≠8+n,
所以点B(4,10)不是“开心点”;
(2)点M在第三象限,
理由如下:
∵点M(a,2a﹣1)是“开心点”,
∴m﹣1=a,,
∴m=a+1,n=4a﹣4,
代入2m=8+n有2a+2=8+4a﹣4,
∴a=﹣1,2a﹣1=﹣3,
∴M(﹣1,﹣3),
故点M在第三象限.
20.(1)根据点的坐标变化可知:
各点的坐标为:A5(2,1),A9(4,1),A13(6,1);
故答案为:2,1,4,1,6,1;
(2)根据(1)发现:
点A4n+1的坐标(n为正整数)为(2n,1);
(3)因为每四个点一个循环,
所以2021÷4=505…1.
所以蜗牛从点A2020到点A2021的移动方向是向上.
21.(1)由动点运动方向与长度可得P3(1,0),P6(2,0),
可以发现脚标是3的倍数的点,依次排列在x轴上,且相距1个单位,
即动点运动三次与横轴相交,
故答案为P9( 3,0),P12(4、0 ),P15(5、0 ).
(2)由(1)可归纳总结点P3n的坐标为P3n(n,0),(n是正整数);
(3)根据(2),∵60=3×20,∴点P60的横坐标是20
故点P60的坐标是(20、0 )
故答案为(20、0 ).
(4)∵210=3×70,符合(2)中的规律
∴点P210在x轴上,
又由图象规律可以发现当动点在x 轴上时,偶数点向上运动,奇数点向下运动,
而点P210是在x轴上的偶数点
所以动点从点P210到点P211的移动方向应该是向上.
22.(1)由题意,知跳马运动一次,则有2种情况,一种为横坐标变化2个单位,纵坐标变化1个单位;另一种为横坐标变化1个单位,纵坐标变化2个单位,
∴P1可能为E(﹣1,﹣1);
(2)P0至P2经两次运动,横坐标变小4个单位,纵坐标不变,则P1可能为P1(7,2)或P1(7,4);
故答案为:P1(7,2)或P1(7,4);
(3)P0为平面上一个定点,则点P7、P26可能与P0重合的是P26;
故答案为:P26;
(4)∵P0在平面直角坐标系内做“跳马运动”,即P0与P2、P4、P6重合,
∴P0P7长的最小值是:.
故答案为:;
(5)从P0至P21共21次变化,每次都向x轴正向运动,则横坐标始终变大,设有x次运动,为横坐标变化2个单位,纵坐标变一个单位,则有(21﹣x)次为纵坐标变化2个单位,横坐标变1个单位,
∴2x+21﹣x=38﹣1,
∴x=16,
设有m次为纵坐标变大1个单位,则有(16﹣m)次变小1单位,有n次纵坐标变大2单位,(5﹣n)次变小2单位,
m+2n﹣(16﹣m)﹣2(5﹣n)=10,
∴m=18﹣2n,
∴纵坐标最大为:m+2n=18.
故答案为:18.
23.(1)∵A1的坐标为(3,1),
∴A2(0,4),A3(﹣3,1),A4(0,﹣2),A5(3,1),
…,
依此类推,每4个点为一个循环组依次循环,
∵2018÷4=504余2,
∴点A2018的坐标与A2的坐标相同,为(0,4);
故答案为:(﹣3,1),(0,4);
(2)∵点A1的坐标为(a,b),
∴A2(﹣b+1,a+1),A3(﹣a,﹣b+2),A4(b﹣1,﹣a+1),A5(a,b),
…,
依此类推,每4个点为一个循环组依次循环,
∵对于任意的正整数n,点An均在x轴上方,
∴,,
解得﹣1<a<1,0<b<2.
24.(1)由题意得d(P,A)=|3﹣5|+|﹣4﹣2|=8,
d(P,B)=|3﹣(﹣1)|+|﹣4﹣0|=8,
d(P,C)=|3﹣(﹣2)|+|﹣4﹣1|=10,
d(P,D)=|3﹣0|+|﹣4﹣1|=8,
故答案为:A,B,D.
(2)d(P,Q)=|3﹣t|+|﹣4﹣2|=10,
解得t=﹣1或t=7.
(3)d(P,Q)=|3﹣t|+|﹣4﹣(t+1)|,
化简得d(P,Q)=|3﹣t|+|5+t|,
当﹣5≤t≤3时,|3﹣t|+|5+t|=3﹣t+5+t=8,满足题意.
当t<﹣5时,|3﹣t|+|5+t|=3﹣t﹣5﹣t=﹣2﹣2t,不满足题意.
当t>3时,|3﹣t|+|5+t|=t﹣3+5+t=2+2t,不满足题意.
∴﹣5≤t≤3.
