北师大版八年级数学上册试题 第一章 《勾股定理》复习题 (含答案)
文档属性
| 名称 | 北师大版八年级数学上册试题 第一章 《勾股定理》复习题 (含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 512.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-17 00:00:00 | ||
图片预览


文档简介
第一章 《勾股定理》复习题
一、选择题。
1.下列四组数据为三角形的三边,其中能构成直角三角形的是( )
A.; B.; C.; D..
2.2002年国际数学家大会在中国北京举行,这次大会的会徽如图所示,选定的是我国古代数学家赵爽用来证明勾股定理的弦图,可以说是充分肯定了我国数学的成就,也弘扬了我国古代的数学文化.弦图是由四个全等的直角三角形和中间的小正方形拼成的一个大正方形.如果大正方形的面积是18,小正方形的面积是2,直角三角形的较短直角边长为a,较长直角边长为b,那么的值为( )
A.18 B.30 C.34 D.364
3.1876年,美国总统伽菲尔德利用如图所示的方法验证了勾股定理,其中两个全等的直角三角形的边,在一条直线上,证明中用到的面积相等关系是( )
A. B.
C. D.
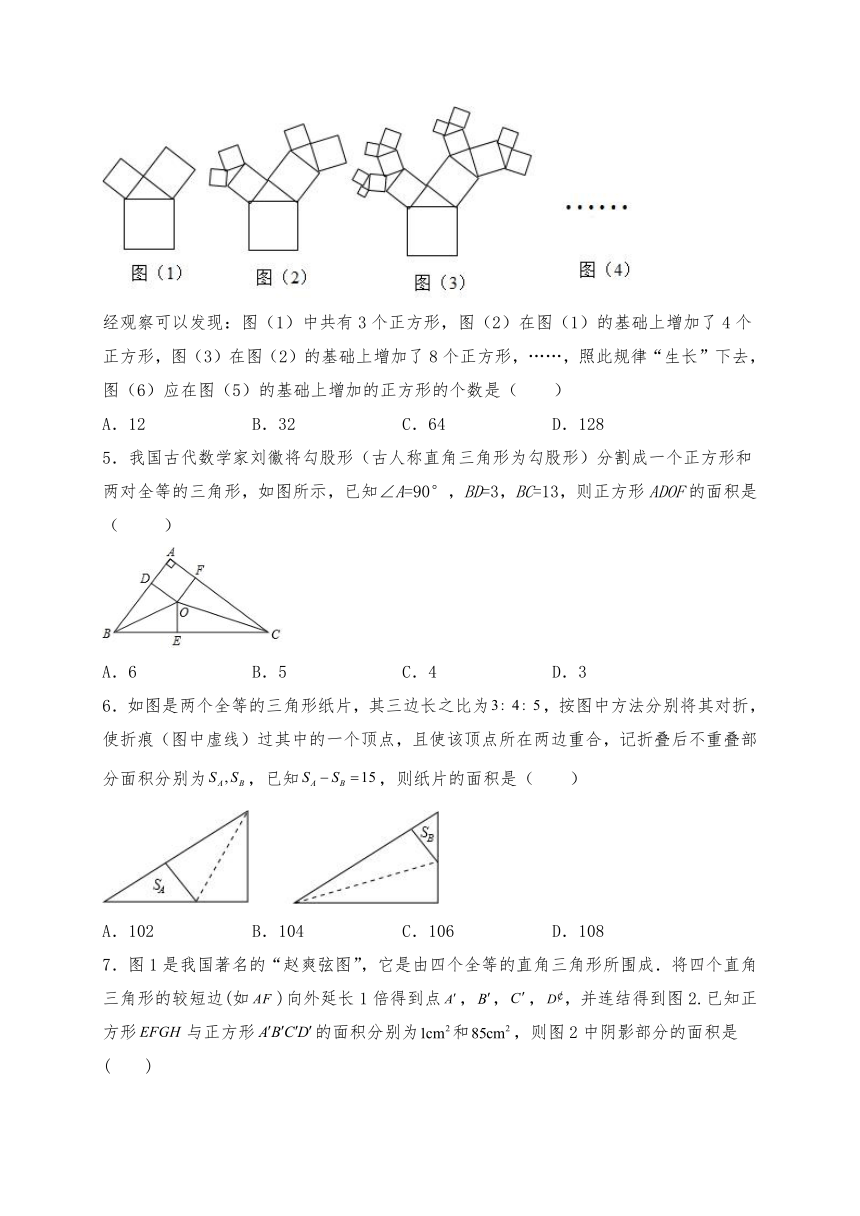
4.如图是按照一定规律“生长”的“勾股树”:
经观察可以发现:图(1)中共有3个正方形,图(2)在图(1)的基础上增加了4个正方形,图(3)在图(2)的基础上增加了8个正方形,……,照此规律“生长”下去,图(6)应在图(5)的基础上增加的正方形的个数是( )
A.12 B.32 C.64 D.128
5.我国古代数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的三角形,如图所示,已知∠A=90°,BD=3,BC=13,则正方形ADOF的面积是( )
A.6 B.5 C.4 D.3
6.如图是两个全等的三角形纸片,其三边长之比为,按图中方法分别将其对折,使折痕(图中虚线)过其中的一个顶点,且使该顶点所在两边重合,记折叠后不重叠部分面积分别为,已知,则纸片的面积是( )
A.102 B.104 C.106 D.108
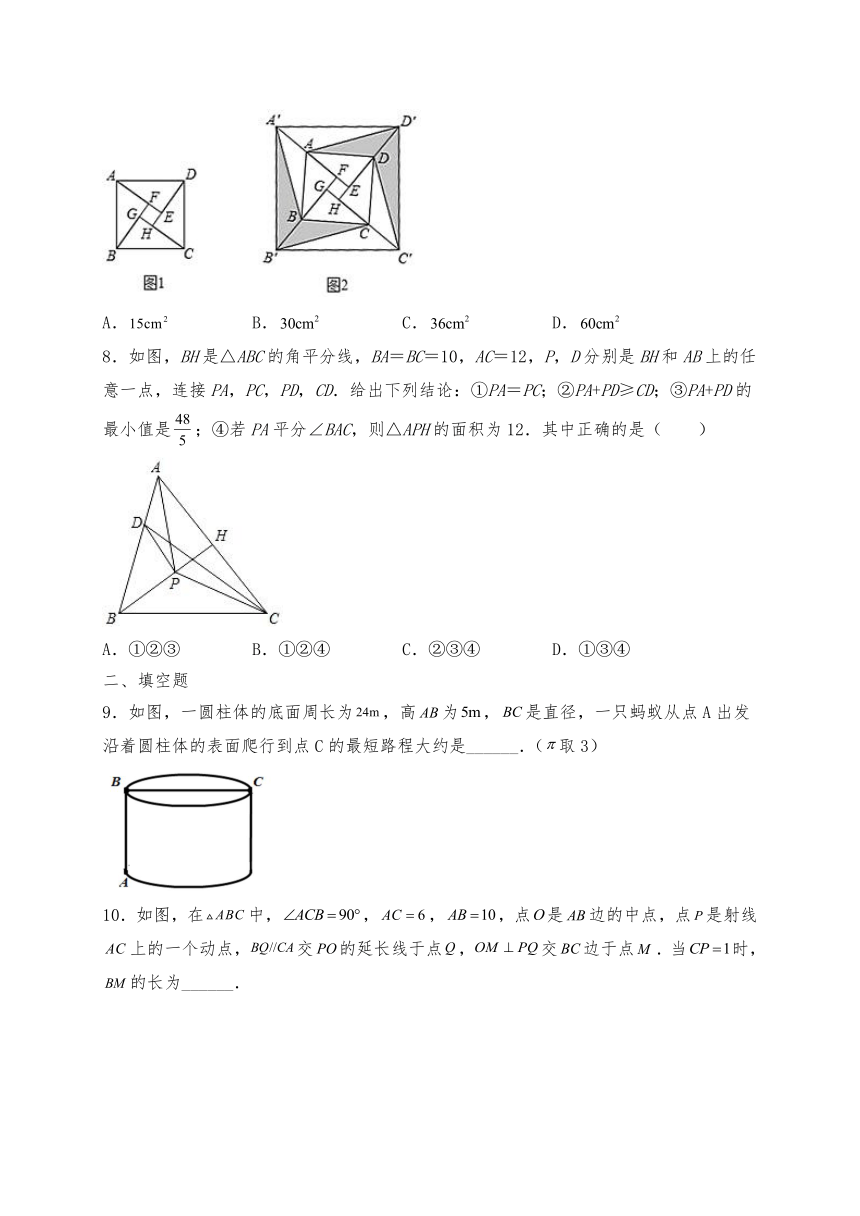
7.图1是我国著名的“赵爽弦图”,它是由四个全等的直角三角形所围成.将四个直角三角形的较短边(如)向外延长1倍得到点,,,,并连结得到图2.已知正方形与正方形的面积分别为和,则图2中阴影部分的面积是( )
A. B. C. D.
8.如图,BH是△ABC的角平分线,BA=BC=10,AC=12,P,D分别是BH和AB上的任意一点,连接PA,PC,PD,CD.给出下列结论:①PA=PC;②PA+PD≥CD;③PA+PD的最小值是;④若PA平分∠BAC,则△APH的面积为12.其中正确的是( )
A.①②③ B.①②④ C.②③④ D.①③④
二、填空题
9.如图,一圆柱体的底面周长为,高为,是直径,一只蚂蚁从点A出发沿着圆柱体的表面爬行到点C的最短路程大约是______.(取3)
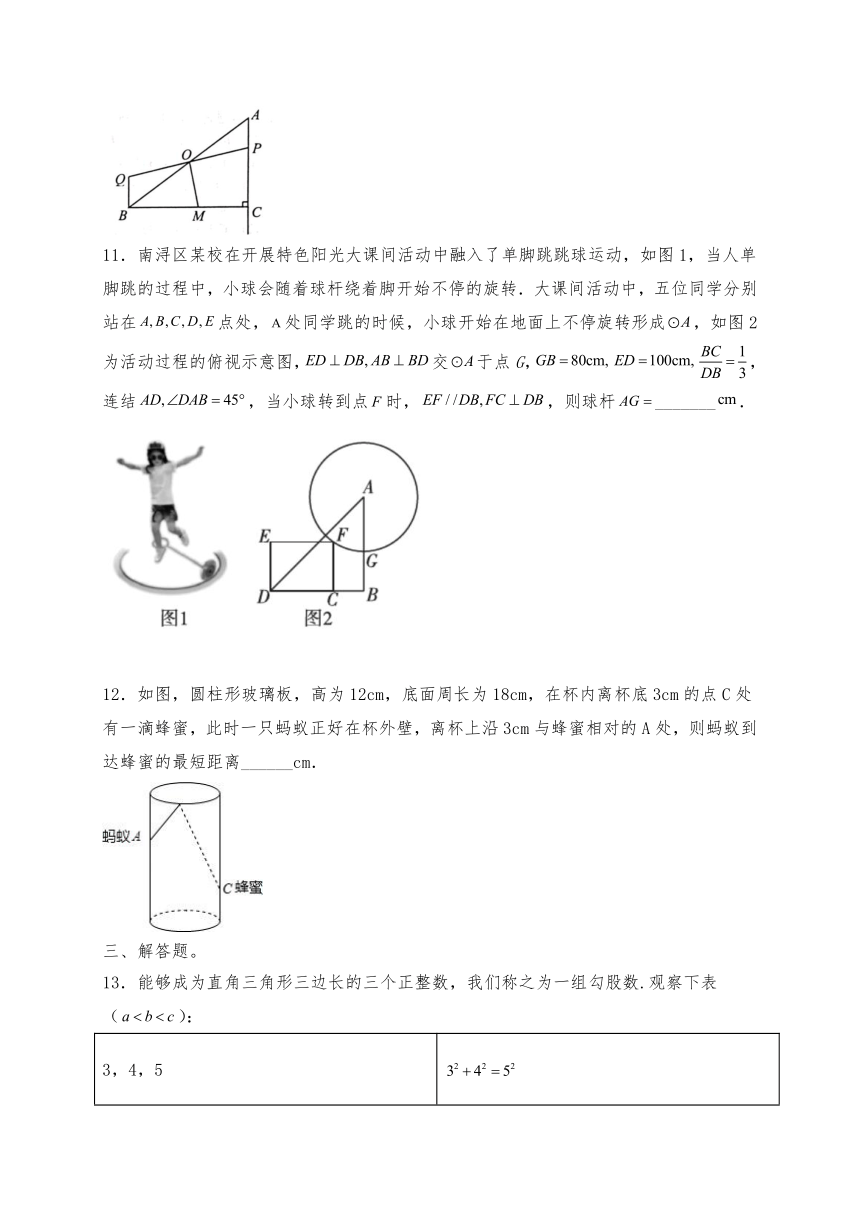
10.如图,在中,,,,点是边的中点,点是射线上的一个动点,交的延长线于点,交边于点.当时,的长为______.
11.南浔区某校在开展特色阳光大课间活动中融入了单脚跳跳球运动,如图1,当人单脚跳的过程中,小球会随着球杆绕着脚开始不停的旋转.大课间活动中,五位同学分别站在点处,处同学跳的时候,小球开始在地面上不停旋转形成,如图2为活动过程的俯视示意图,交于点G,,连结,当小球转到点时,,则球杆_______.
12.如图,圆柱形玻璃板,高为12cm,底面周长为18cm,在杯内离杯底3cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿3cm与蜂蜜相对的A处,则蚂蚁到达蜂蜜的最短距离______cm.
三、解答题。
13.能够成为直角三角形三边长的三个正整数,我们称之为一组勾股数.观察下表():
3,4,5
5,12,13
7 ,24 ,25
9,40,41
… …
(1)试找出它们的共同点,由它们的共同点得出并证明一个结论;
(2)写出当时,,的值.
14.台风是一种自然灾害,它以台风中心为圆心在周围上百千米的范围内形成极端气候,有极强的破坏力,如图,有一台风中心沿东西方向由行驶向,已知点为一海港,且点与直线上的两点,的距离分别为,,又,以台风中心为圆心周围以内为受影响区域.
(1)求的度数.
(2)海港受台风影响吗?为什么?
(3)若台风的速度为千米/小时,当台风运动到点处时,海港刚好受到影响,当台风运动到点时,海港刚好不受影响,即,则台风影响该海港持续的时间有多长?
15.在中,,,点在直线上(除外),分别经过点和点作和的垂线,两条垂线交于点,研究和的数量关系.
(1)某数学兴趣小组在探究的关系时,运用“从特殊到一般”的数学思想,他们发现当点是的中点时,只需要取边的中点(如图1),通过推理证明就可以得到和的数量关系,请你按照这种思路直接写出和的数量关系;
(2)那么当点是直线上(除外)(其它条件不变),上面得到的结论是否仍然成立呢?请你从“点在线段上”,“点在线段的延长线”,“点在线段的反向延长线上”三种情况中,任选一种情况,在图2中画出图形,并证明你的结论;
(3)当点在线段的延长线上时,若(),请直接写出的值.
答案
一、选择题。
D.C.B.C.C.D.B.A.
二、填空题
9.13
10.2.5或1.
11.100.
12.15.
三、解答题
13.(1)共同点:①各组数均满足;②最小的数是奇数,其余的两个数是连续的正整数;③最小的数的平方等于另两个连续整数的和,如,,,.
由以上共同点可以得出这样一个结论:设为大于1的奇数,将拆分为两个连续的正整数之和,即,则,,就构成一组勾股数.
证明:因为(为大于I的奇数),
所以,
所以,,是一组勾股数.
(2)由(1)中结论可知,当时,因为,所以 ,.
14.(1),,,
,
是直角三角形,
∴∠ACB=90°;
(2)海港受台风影响,
过点作,
是直角三角形,
,
,
,
以台风中心为圆心周围以内为受影响区域,
海港受台风影响.
(3)当,时,正好影响港口,
,
,
台风的速度为千米/小时,
(小时)
答:台风影响该海港持续的时间为小时.
15.解:(1),
连接GE
∵,点是的中点,点G为AC的中点
∴AG=CG=CE=EB,
因为,
所以,.
所以.
因为,,
所以,
所以.
所以.
在与中,
所以.
所以
(2)仍然成立.
在上截取,连接.
因为,
所以.
因为,,
所以,
所以.
所以.
因为,
所以,.
所以.
在与中,
所以.
所以.
(3)如下图所示,在的延长线上截取,连接,AF
因为,
所以.
因为,,
所以,
所以.
所以.
因为,
所以,
∴∠EBF=180°-∠ABF-∠ABC=45°.
所以.
在与中,
所以.
所以.
∴为等腰直角三角形
设CA=CB=a,则
∴CE=a+na
由勾股定理可得AE==
∴,
∴.
一、选择题。
1.下列四组数据为三角形的三边,其中能构成直角三角形的是( )
A.; B.; C.; D..
2.2002年国际数学家大会在中国北京举行,这次大会的会徽如图所示,选定的是我国古代数学家赵爽用来证明勾股定理的弦图,可以说是充分肯定了我国数学的成就,也弘扬了我国古代的数学文化.弦图是由四个全等的直角三角形和中间的小正方形拼成的一个大正方形.如果大正方形的面积是18,小正方形的面积是2,直角三角形的较短直角边长为a,较长直角边长为b,那么的值为( )
A.18 B.30 C.34 D.364
3.1876年,美国总统伽菲尔德利用如图所示的方法验证了勾股定理,其中两个全等的直角三角形的边,在一条直线上,证明中用到的面积相等关系是( )
A. B.
C. D.
4.如图是按照一定规律“生长”的“勾股树”:
经观察可以发现:图(1)中共有3个正方形,图(2)在图(1)的基础上增加了4个正方形,图(3)在图(2)的基础上增加了8个正方形,……,照此规律“生长”下去,图(6)应在图(5)的基础上增加的正方形的个数是( )
A.12 B.32 C.64 D.128
5.我国古代数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的三角形,如图所示,已知∠A=90°,BD=3,BC=13,则正方形ADOF的面积是( )
A.6 B.5 C.4 D.3
6.如图是两个全等的三角形纸片,其三边长之比为,按图中方法分别将其对折,使折痕(图中虚线)过其中的一个顶点,且使该顶点所在两边重合,记折叠后不重叠部分面积分别为,已知,则纸片的面积是( )
A.102 B.104 C.106 D.108
7.图1是我国著名的“赵爽弦图”,它是由四个全等的直角三角形所围成.将四个直角三角形的较短边(如)向外延长1倍得到点,,,,并连结得到图2.已知正方形与正方形的面积分别为和,则图2中阴影部分的面积是( )
A. B. C. D.
8.如图,BH是△ABC的角平分线,BA=BC=10,AC=12,P,D分别是BH和AB上的任意一点,连接PA,PC,PD,CD.给出下列结论:①PA=PC;②PA+PD≥CD;③PA+PD的最小值是;④若PA平分∠BAC,则△APH的面积为12.其中正确的是( )
A.①②③ B.①②④ C.②③④ D.①③④
二、填空题
9.如图,一圆柱体的底面周长为,高为,是直径,一只蚂蚁从点A出发沿着圆柱体的表面爬行到点C的最短路程大约是______.(取3)
10.如图,在中,,,,点是边的中点,点是射线上的一个动点,交的延长线于点,交边于点.当时,的长为______.
11.南浔区某校在开展特色阳光大课间活动中融入了单脚跳跳球运动,如图1,当人单脚跳的过程中,小球会随着球杆绕着脚开始不停的旋转.大课间活动中,五位同学分别站在点处,处同学跳的时候,小球开始在地面上不停旋转形成,如图2为活动过程的俯视示意图,交于点G,,连结,当小球转到点时,,则球杆_______.
12.如图,圆柱形玻璃板,高为12cm,底面周长为18cm,在杯内离杯底3cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿3cm与蜂蜜相对的A处,则蚂蚁到达蜂蜜的最短距离______cm.
三、解答题。
13.能够成为直角三角形三边长的三个正整数,我们称之为一组勾股数.观察下表():
3,4,5
5,12,13
7 ,24 ,25
9,40,41
… …
(1)试找出它们的共同点,由它们的共同点得出并证明一个结论;
(2)写出当时,,的值.
14.台风是一种自然灾害,它以台风中心为圆心在周围上百千米的范围内形成极端气候,有极强的破坏力,如图,有一台风中心沿东西方向由行驶向,已知点为一海港,且点与直线上的两点,的距离分别为,,又,以台风中心为圆心周围以内为受影响区域.
(1)求的度数.
(2)海港受台风影响吗?为什么?
(3)若台风的速度为千米/小时,当台风运动到点处时,海港刚好受到影响,当台风运动到点时,海港刚好不受影响,即,则台风影响该海港持续的时间有多长?
15.在中,,,点在直线上(除外),分别经过点和点作和的垂线,两条垂线交于点,研究和的数量关系.
(1)某数学兴趣小组在探究的关系时,运用“从特殊到一般”的数学思想,他们发现当点是的中点时,只需要取边的中点(如图1),通过推理证明就可以得到和的数量关系,请你按照这种思路直接写出和的数量关系;
(2)那么当点是直线上(除外)(其它条件不变),上面得到的结论是否仍然成立呢?请你从“点在线段上”,“点在线段的延长线”,“点在线段的反向延长线上”三种情况中,任选一种情况,在图2中画出图形,并证明你的结论;
(3)当点在线段的延长线上时,若(),请直接写出的值.
答案
一、选择题。
D.C.B.C.C.D.B.A.
二、填空题
9.13
10.2.5或1.
11.100.
12.15.
三、解答题
13.(1)共同点:①各组数均满足;②最小的数是奇数,其余的两个数是连续的正整数;③最小的数的平方等于另两个连续整数的和,如,,,.
由以上共同点可以得出这样一个结论:设为大于1的奇数,将拆分为两个连续的正整数之和,即,则,,就构成一组勾股数.
证明:因为(为大于I的奇数),
所以,
所以,,是一组勾股数.
(2)由(1)中结论可知,当时,因为,所以 ,.
14.(1),,,
,
是直角三角形,
∴∠ACB=90°;
(2)海港受台风影响,
过点作,
是直角三角形,
,
,
,
以台风中心为圆心周围以内为受影响区域,
海港受台风影响.
(3)当,时,正好影响港口,
,
,
台风的速度为千米/小时,
(小时)
答:台风影响该海港持续的时间为小时.
15.解:(1),
连接GE
∵,点是的中点,点G为AC的中点
∴AG=CG=CE=EB,
因为,
所以,.
所以.
因为,,
所以,
所以.
所以.
在与中,
所以.
所以
(2)仍然成立.
在上截取,连接.
因为,
所以.
因为,,
所以,
所以.
所以.
因为,
所以,.
所以.
在与中,
所以.
所以.
(3)如下图所示,在的延长线上截取,连接,AF
因为,
所以.
因为,,
所以,
所以.
所以.
因为,
所以,
∴∠EBF=180°-∠ABF-∠ABC=45°.
所以.
在与中,
所以.
所以.
∴为等腰直角三角形
设CA=CB=a,则
∴CE=a+na
由勾股定理可得AE==
∴,
∴.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
