2.4 整式 课件（共34页）

(共34张PPT)
第2章 代数式
2.4 整 式
湘教版七年级上册
教学目标
1.通过具体实例理解单项式、多项式、整式的概念.
2.理解单项式的系数、次数，多项式的项数、次数等概念.（重点、难点）
创设情境
（1）长为x，宽为0.8x的长方形的面积是多少？
（2）半径为r的圆的面积是多少？
（3）长方体的底面是边长为x的正方形，高为y，这个长方体的体积是多少？
讲授新课
单项式的相关概念
一
用含有字母的式子填空
1. 棱长为a的正方形的表面积为____ ;体积为_ __.
3. 一辆汽车的速度是vkm/h,它t小时的行驶路程为 km.
2. 铅笔的单价为x元,圆珠笔的单价是铅笔的单价2.5倍,圆珠笔的单价是 元.
vt
2.5x
6a2
a3
4. 一个圆的半径是r cm，它周长是 cm.
2πr
思考： 6a2，a3，2.5x，vt，2πr 以上各式中运算
有什么共同特点？
上面各式的运算中数字和字母之间，字母与字母之间的运算都是乘法运算(都是表示字母与数字、字母与字母的积).
这样的式子叫做单项式，单独的一个数或一个字母也是单项式.
例如:像-2,a,-b, 等是单项式.
注意:像 , , 等不是单项式.
为什么？
概念学习
练一练
下列式子中哪些是单项式
√
√
√
√
√
√
1.单独一个数或一个字母也是单项式.
2.不含加减运算，单项式只含有乘积运算.
3.单项式数字因数与字母可能一个或多个.
4.可以含有除以数的运算，不能含有除以字母的运算．
判断单项式的方法:
方法总结
单项式中，与字母相乘的数叫做单项式的系数。
例如 0.8x2的系数是0.8；
πr2的系数是π；
x2y的系数是1；
–x的系数是–1。
一个单项式中，所有字母的指数的和叫做这个单项式的次数。
例如 0.8x2的次数是2； πr2的次数是2；
x2y的次数是3； –x的次数是1。
如果单项式只是一个数，并且这个数不是0，那么它的次数是0.
例如，单项式 的次数是0。
(1)每包书有12册,n包书有_____册；
(2) 底边长为a,高为h的三角形的面积是_____；
(3) 一个长方体的长和宽都是a,高为h,它的体积是_____；
(4)一台电视机原价为a元,现按原价的九折出售,这台电视机现在的售价为____；
(5)一个长方形的长为0.9,宽为a,面积是____.
1
2.用单项式填空,并指出它们的系数和次数:
12n
0.9a
0.9a
一次
二次
三次
一次
一次
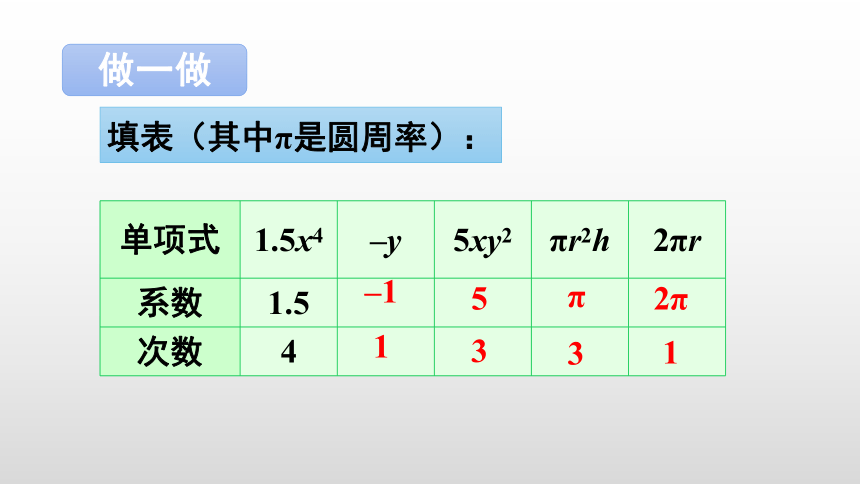
做一做
填表（其中π是圆周率）：
单项式 1.5x4 –y 5xy2 πr2h 2πr
系数 1.5
次数 4
–1
1
5
3
3
π
2π
1
1.单项式的系数：单项式中的数字因数．若一个单项式只含有字母因数，那么它的系数就是1或－1；若单项式是单独一个数，则系数就是它本身．
2.单项式的次数应是该单项式中所有字母的指数和，与系数的指数没关系，如24x2y3的次数是5，而不是9；单独一个数的次数是0.
3.不要把π当成字母．
归纳总结
练一练
1.判断下列说法是否正确：
①－7xy2的系数是7；（ ）
②－x2y3与x3没有系数；（ ）
③－ab3c2的次数是0＋3＋2；（ ）
④－a3的系数是－1； （ ）
⑤－32x2y3的次数是7；（ ）
⑥ πr2h的系数是 .（ ）
×
×
×
×
×
√
π是系数的一部分
－32是系数
勿遗漏a的指数1
任何单项式都有系数
下图是某拱形门的示意图，它是由上、下两部分组成的.已知上部分的面积为 ，下部分的面积为xy，则这个图形的面积是多少（结果保留π）？
说一说
该图形的面积是 。
可以看做是单项式 与xy的和。
2x3 – 5x2y+3xy – 1可以看做是单项式2x3，–5x2y，3xy与–1的和.
像这样，由几个单项式的和组成代数式叫做多项式。
组成多项式的每个单项式叫做多项式的项，其中不含字母的项叫常数项。
2x3 – 5x2y + 3xy – 1
项
常数项
多项式中次数最高的项的次数，叫做这个多项式的次数。
2x3 – 7x2+9的次数是3。
习惯上把单项式和多项式统称为整式。
多项式的项
2x 3 – 7x2 + 9
多项式的次数
说出下列多项式的次数和常数项：
（1）2x-3；
（2）-x3+7x -4；
（3）3x2 -5xy + y2-4x + 6y -9 .
例
解（1）2x-3的次数是1，常数项是-3.
（2）-x3+7x-4的次数是 3，常数项是-4.
（3） 3x2-5xy+y2-4x+6y-9的次数是 2，常数项是-9.
x
32t3
1
32
1
3
0
6
3
解:
1
4
2
要点归纳：
(1)多项式的各项应包括它前面的符号
(3)要确定一个多项式的次数，先要确定此多项式中各项(单项式)的次数，然后找次数最高的
(4)一个多项式的最高次项可以不唯一
(2)多项式没有系数的概念，但其每一项均有系数，每一项的系数也包括前面的符号
例4 已知－5xm＋104xm+1－4xmy2是关于x、y的六次多项式，求m的值，并写出该多项式.
解：由题意得m＋2=6，所以m=4.
归纳总结：解题的关键是弄清多项式次数是多项式中次数最高的项的次数.然后根据题意，列出方程，求出m的值.
分析：该多项式最高次项为－4xmy2，其次数为m＋2，故m＋2=6.
所以该多项式为－5x4＋104x5－4x4y2.
【变式】若关于x的多项式－5x3－mx2＋（n－1）x－1不含二次项和一次项，求m、n的值.
解：∵关于x的多项式－5x3－mx2＋(n－1)x－1不含二次项和一次项，
∴m＝0，n－1＝0，
则m＝0，n＝1.
做一做
1.多项式x2+y－z是单项式___，___，___的
和，它是___次___项式.
2.多项式3m3－2m－5+m2的常数项是____，二次
项是_____，二次项的系数是_____.
x2
y
－z
二
三
－5
m2
1
1. 说出下列单项式的系数和次数：
（1） 2x3； （2） ；
（3）-x； （4） ；
（5） .
系数是 ，次数是1.
系数是2，次数是3.
系数是 ，次数是3.
系数是-1，次数是1.
系数是 ，次数是4.
课堂练习
（1）-3x+11； （2）5x2-2x+7 ；
（3）x2-2xy+y2-3x+5y-1； （4）y2-x3+x-2.
2.说出下列多项式的次数和常数项：
（1） -3x+11的次数为1，常数项为11；
（2） 5x2-2x+7 的次数为2，常数项为7；
（3） x2-2xy+y2-3x+5y-1 的次数为2，常数项为-1；
（4） y2-x3+x-2 的次数为3，常数项为-2.
解
3.下列代数式哪些是多项式？哪些不是多项式？
（1）x4-5x3+7x-3； （2） ；
（3） ； （4） x2 + x +1.
√
√
×
×
4.下列式子中，哪些是单项式？哪些是多项式？哪些是整式？
3x，2x-1， ，-ab，-5， -1，3m-4n+m2n．
5.判断正误：
（1）多项式-x2y+2x2-y的次数2．（ ）
（2）多项式 - -a+3a2的一次项系数是1．（ ）
（3）-x-y-z是三次三项式．（ ）
6.一个关于字母x的二次三项式的二次项系数为４，一次项系数为１，常数项为7，则这个二次三项式为＿＿＿．
×
×
×
4x2+x+7
课堂小结
整式
单项式
多项式
由数与字母的积组成的代数式叫单项式
单独一个字母或一个数也是单项式
单项式中，与字母相乘的数叫做单项式的系数
单项式中所有字母的指数的和叫做这个单项式的次数
由几个单项式的和组成的代数式叫做多项式
不含字母的项叫做常数项
多项式中次数最高的项的次数叫做这个多项式的次数
组成多项式的每个单项式叫做多项式的项
谢谢
21世纪教育网（www.21cnjy.com)
中小学教育资源网站
兼职招聘：
https://www.21cnjy.com/recruitment/home/admin