人教版七上第二章 整式的加减 章末复习课件(共32张PPT)
文档属性
| 名称 | 人教版七上第二章 整式的加减 章末复习课件(共32张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 6.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-17 08:32:14 | ||
图片预览











文档简介
(共32张PPT)
第二章整式
全章总复习
人教版七年级上册
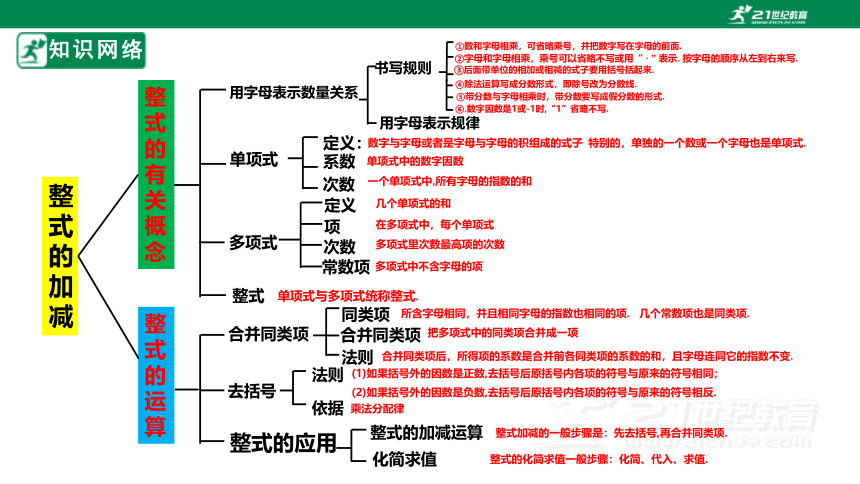
用字母表示数量关系
整式的有关概念
整式的运算
整式的应用
单项式
多项式
整式
合并同类项
去括号
化简求值
整式的加减运算
定义:
次数
系数
定义
次数
项
常数项
知识网络
整式的加减
合并同类项
同类项
法则
依据
用字母表示规律
书写规则
数字与字母或者是字母与字母的积组成的式子
特别的,单独的一个数或一个字母也是单项式.
单项式中的数字因数
一个单项式中,所有字母的指数的和
几个单项式的和
在多项式中,每个单项式
多项式里次数最高项的次数
多项式中不含字母的项
单项式与多项式统称整式.
所含字母相同,并且相同字母的指数也相同的项.
几个常数项也是同类项.
把多项式中的同类项合并成一项
合并同类项后,所得项的系数是合并前各同类项的系数的和,且字母连同它的指数不变.
法则
(1)如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同;
(2)如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反.
乘法分配律
①数和字母相乘,可省略乘号,并把数字写在字母的前面.
③后面带单位的相加或相减的式子要用括号括起来.
④除法运算写成分数形式,即除号改为分数线.
⑤带分数与字母相乘时,带分数要写成假分数的形式.
⑥.数字因数是1或-1时,“1”省略不写.
②字母和字母相乘,乘号可以省略不写或用“ · ” 表示. 按字母的顺序从左到右来写.
整式加减的一般步骤是:先去括号,再合并同类项.
整式的化简求值一般步骤:化简、代入、求值.
考点一:用字母表示数量关系
典型例题
例1用字母表示下列数量关系:
(1). “x的2倍与y的三分之一的和”.
(2). 已知某工厂1月的产值为m万元,若2月、3月每月的增长率都是n%,则9月、10月的产值分别是多少万元
分析:x的2倍为2x,y的三分之一为将它们相加可得.
解:(1). “x的2倍与y的三分之一的和”为:
典型例题
分析:
(2)由2月的增长率是n%,得2月的产值=1月的产值×(1+n%).
同理.3月的产值=2月的产值×(1+n%).
解:(2) 因为2月、3月每月的增长率都是n%,所以2月的产值为%)万元,3月的产值为万元.
归纳
用字母表示数量关系要注意以下五点:
(5).有时需要将题中的字母代入公式,这就要求正确进行代换.
(4).规范书写格式
(3).注意运算顺序,在语言叙述的数量关系中,读的先写,不同级运算的语言要体现出先低级运算
(2).分清数量关系
(1). 抓住关键词语,仔细辨别词义
例2 已知多项式 5a2bm+1 +3a3b 5a2+1是五次多项式,单项式3an+1b的次数与这个多项式的次数相同,求(m n)2022的值.
考点二 整式的相关概念
分析:多项式 5a2bm+1 +3a3b 5a2+1是五次多项式,得最高次项 5a2bm+1的次数是5,从而求得m,再由单项式3an+1b的次数为5,求得n的值,最后求得(m n)2022的值.
典型例题
解:因为多项式 5a2bm+1 +3a3b 5a2+1是五次多项式,得最高次项 5abm+1的次数是5.
所以m+1=5
m=2
因为单项式3an+1b的次数与这个多项式的次数相同,
所以(n+1)+1=5
n=3
所以(m n)2022=(2 3)2022=( 1)2022=1
答:当m=2,n=3时,(m n)2022=1
典型例题
考点三 整式的加减运算
例3. (2x2 y2) 2(3y2 2x2)
解:(2x2 y2) 2(3y2 2x2)
=6x2 7y2
=(2x2 y2) (6y2 4x2)
=2x2 y2 6y2+4x2
典型例题
1.整式的加减运算
例4 (1)先化简,再求值ab2 3a2b 3(ab2 a2b),其中a=2,b= 1.
2.整式的化简求值
解:ab2 3a2b 3(ab2 a2b)
=ab2 3a2b (3ab2 3a2b)
=ab2 3a2b 3ab2+3a2b
= 2a2b
当a=2,b= 1时,原式= 2╳22 ╳( 1)=4.
直接化简求值法
典型例题
(2).若多项式x2+2x 8=0,求2x2+4x 17的值.
整体代入法
分析:没有直接求出的x值,如果把x2+2x看成一个整体, 2x2+4x是x2+2x的2倍,代入就可以求出2x2+4x 17的值.
解:2x2+4x 17
因为x2+2x 8=0,得x2+2x=8,
当x2+3x=3时,原式=2 ×8 17= 1
=2(x2+2x) 7
典型例题
(2).若多项式x2+2x 8=0,求2x2+4x 17的值.
(2).规律性
①.数与式的规律.
典型例题
观察下列有规律的数 ….根据其规律,则
(1)第7个数是________;
(2)第n个数是________;
(3) 是第________个数;
(4)计算: .
12
解:(1)由题可知: , , , , ,
(4)解:原式 ,
.
∴ 是第12个数;
(3)根据题意可得: ,
(2)由(1)可得:第n个数是 ;
, 所以第7个数为: ;
②.图形的规律.
典型例题
一张长方形桌子可坐6人,按图3将桌子拼在一起.
(1)2张桌子拼在一起可坐________人,4张桌子拼在一起可坐________人,n张桌子拼在一起可坐________人;
(2)一家餐厅有40张这样的长方形桌子,按照上图的方式每5张拼成1张大桌子,则40张桌子可拼成8张大桌子,共可坐多少人?
(2). (4+2×5)×8=(4+10)×8=14×8=112(人),
n张桌子拼在一起可坐:(4+2n)人;
4张桌子拼在一起可坐:4+2×4=4+8=12(人),
2张桌子拼在一起可坐:4+2×2=4+4=8(人),
解:(1)由图可得,
1. 苹果每千克m元,梨每千克n元购买x千克苹果和y千克梨的用了( ) 元.
(mx+ny)元 B. (nx+my)元
C. mn(x+y)元 D. (m+n)(x+y)元
2. 用式子表示“a 的2倍与b 的的和,结果为( ) .
2a+ b B. (a+b)
C. (2a+b) D. 2(a+ b)
A
A
强化训练
强化训练
3. 下列式子中,是单项式的是( )
A. B. x3yz2 C. D. x y
4. 下列说法不正确的是( )
A. 的系数是
B. 2不是单项式
C. 单项式的次数是2
D. 是多项式
B
B
强化训练
5. 下列各式中:ab, , ab2+b+1,+ , x3+ x2-3中,多项式有( )
A. 2个 B. 3个 C. 4个 D. 5个
6. 下列各式中,不是整式的是( )
A. B. x-y C. D. 4x
B
A
强化训练
7. 下列判断中正确的是( )
是单项式
B. 不是单项式
C. 单项式 和 是同类项
D. +2 + +1 是三次三项式
C
强化训练
8. 若A是一个三次多项式,B是一个四次多项式,则A+B一定是( )
三次多项式
B. 四次多项式或单项式
C. 七次多项式
D. 四次七项式
B
强化训练
10.下列整式运算不正确的是( )
A.
B.
C.
D.
9. 下列各式中,与多项式 相等的是( )
A. B.
C. D.
A
B
强化训练
11. 计算:
(1). 2( 2xy2-x2y) -3(xy+2xy2)-x2y;
(2). a2 -[a2+(3a2 -a) -3(a2 -3a)].
解:(1). 2( 2xy2-x2y) -3(xy+2xy2)-x2y
=( 4xy2-2x2y) -(3xy+6xy2)-x2y
=4xy2-2x2y-3xy-6xy2-x2y
=-3x2y-3xy-2xy2
强化训练
=a2-[a2+3a2 -a -3a2 +9a]
=a2-[a2+8a]
=a2-a2-8a
=-8a
11. 计算:
(1). 2( 2xy2-x2y) -3(xy+2xy2)-x2y;
(2). a2 -[a2+(3a2 -a) -3(a2 -3a)].
解:(2). a2 -[a2+(3a2 -a) -3(a2 -3a)].
强化训练
12. 已知 , .
(1).求 .
(2).当 , 时,求 的值.
解:(1)
解: (2)当 , 时,
;
强化训练
13. 下面是小彬同学进行整式化简的过程,请认真阅读并完成相应任务.
3(3xy﹣x2)﹣2(2x2 xy)
=9xy﹣3x2﹣(4x2 2xy)...........................①
=9xy﹣3x2﹣4x2﹣2xy ..........................②
=7xy﹣7x2 ...................................③
(1):填空:
①以上化简步骤中,第一步的依据是 ;
;②以上化简步骤中,第 步开始出现不符合题意,这一步错误的原因是 .
去括号时,括号前面是号,去掉括号和号,括号内的第二项没有变号
根据乘法分配律
②
解:3(3xy﹣x2)﹣2(2x2 xy)
=9xy﹣3x2﹣(4x2 2xy)
=9xy﹣3x2﹣4x2+2xy
=11xy﹣7x2
当x=-1,y= 时,
原式=11×(-1)×( ) -7×(-1)2=1-7=-6
(2):请写出该整式正确的化简结果,并计算当x=-1,y= 时该整式的值.
强化训练
14. 某医院原有(4m2﹣6m)剂新冠疫苗,上午打了(5m+3)剂,中午休息时又调来(m2+3m)剂,晚上5时发现疫只剩余2(m﹣1)剂.
请问:
(1).该医院中午过后一共打了多少剂新冠疫苗?(用含有m的式子表达)
(2).当m=7时,该医院中午过后一共打了多少剂新冠疫苗?
(1)解:由题意得,
∴该医院中午过后一共打了174剂新冠疫苗.
(2)解:当m=7时,
=
∴该医院中午过后一共打了( )剂新冠疫苗;
=
(4m2﹣6m)-(5m+3)+(m2+3m)-2(m﹣1)
强化训练
(1). 摆第4个图案用________根火柴棒.
(2).按照这种方式摆下去,摆第n个图案用________根火柴棒.
(3). 计算一下摆481根火柴棒时,是第几个图案?
15. 如图是由一些火柴棒搭成的图案.
解:(1)解:由题目得,第①个图案所用的火柴数:
1+4×4=17
第④个图案所用的火柴数:
1+4×3=13
第③个图案所用的火柴数:
1+4×2=9
第②个图案所用的火柴数:
1+4×1=5
强化训练
(2)解:按(1)的方法,依此类推
(3)解:由题意得,
故摆第n个图案用的火柴棒是4n+1
1+4×n=4n+1
第n个图案中,所用的火柴数为:
答:摆481根火柴棒时,是第120个图案.
解得n=120
4n+1=481
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
第二章整式
全章总复习
人教版七年级上册
用字母表示数量关系
整式的有关概念
整式的运算
整式的应用
单项式
多项式
整式
合并同类项
去括号
化简求值
整式的加减运算
定义:
次数
系数
定义
次数
项
常数项
知识网络
整式的加减
合并同类项
同类项
法则
依据
用字母表示规律
书写规则
数字与字母或者是字母与字母的积组成的式子
特别的,单独的一个数或一个字母也是单项式.
单项式中的数字因数
一个单项式中,所有字母的指数的和
几个单项式的和
在多项式中,每个单项式
多项式里次数最高项的次数
多项式中不含字母的项
单项式与多项式统称整式.
所含字母相同,并且相同字母的指数也相同的项.
几个常数项也是同类项.
把多项式中的同类项合并成一项
合并同类项后,所得项的系数是合并前各同类项的系数的和,且字母连同它的指数不变.
法则
(1)如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同;
(2)如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反.
乘法分配律
①数和字母相乘,可省略乘号,并把数字写在字母的前面.
③后面带单位的相加或相减的式子要用括号括起来.
④除法运算写成分数形式,即除号改为分数线.
⑤带分数与字母相乘时,带分数要写成假分数的形式.
⑥.数字因数是1或-1时,“1”省略不写.
②字母和字母相乘,乘号可以省略不写或用“ · ” 表示. 按字母的顺序从左到右来写.
整式加减的一般步骤是:先去括号,再合并同类项.
整式的化简求值一般步骤:化简、代入、求值.
考点一:用字母表示数量关系
典型例题
例1用字母表示下列数量关系:
(1). “x的2倍与y的三分之一的和”.
(2). 已知某工厂1月的产值为m万元,若2月、3月每月的增长率都是n%,则9月、10月的产值分别是多少万元
分析:x的2倍为2x,y的三分之一为将它们相加可得.
解:(1). “x的2倍与y的三分之一的和”为:
典型例题
分析:
(2)由2月的增长率是n%,得2月的产值=1月的产值×(1+n%).
同理.3月的产值=2月的产值×(1+n%).
解:(2) 因为2月、3月每月的增长率都是n%,所以2月的产值为%)万元,3月的产值为万元.
归纳
用字母表示数量关系要注意以下五点:
(5).有时需要将题中的字母代入公式,这就要求正确进行代换.
(4).规范书写格式
(3).注意运算顺序,在语言叙述的数量关系中,读的先写,不同级运算的语言要体现出先低级运算
(2).分清数量关系
(1). 抓住关键词语,仔细辨别词义
例2 已知多项式 5a2bm+1 +3a3b 5a2+1是五次多项式,单项式3an+1b的次数与这个多项式的次数相同,求(m n)2022的值.
考点二 整式的相关概念
分析:多项式 5a2bm+1 +3a3b 5a2+1是五次多项式,得最高次项 5a2bm+1的次数是5,从而求得m,再由单项式3an+1b的次数为5,求得n的值,最后求得(m n)2022的值.
典型例题
解:因为多项式 5a2bm+1 +3a3b 5a2+1是五次多项式,得最高次项 5abm+1的次数是5.
所以m+1=5
m=2
因为单项式3an+1b的次数与这个多项式的次数相同,
所以(n+1)+1=5
n=3
所以(m n)2022=(2 3)2022=( 1)2022=1
答:当m=2,n=3时,(m n)2022=1
典型例题
考点三 整式的加减运算
例3. (2x2 y2) 2(3y2 2x2)
解:(2x2 y2) 2(3y2 2x2)
=6x2 7y2
=(2x2 y2) (6y2 4x2)
=2x2 y2 6y2+4x2
典型例题
1.整式的加减运算
例4 (1)先化简,再求值ab2 3a2b 3(ab2 a2b),其中a=2,b= 1.
2.整式的化简求值
解:ab2 3a2b 3(ab2 a2b)
=ab2 3a2b (3ab2 3a2b)
=ab2 3a2b 3ab2+3a2b
= 2a2b
当a=2,b= 1时,原式= 2╳22 ╳( 1)=4.
直接化简求值法
典型例题
(2).若多项式x2+2x 8=0,求2x2+4x 17的值.
整体代入法
分析:没有直接求出的x值,如果把x2+2x看成一个整体, 2x2+4x是x2+2x的2倍,代入就可以求出2x2+4x 17的值.
解:2x2+4x 17
因为x2+2x 8=0,得x2+2x=8,
当x2+3x=3时,原式=2 ×8 17= 1
=2(x2+2x) 7
典型例题
(2).若多项式x2+2x 8=0,求2x2+4x 17的值.
(2).规律性
①.数与式的规律.
典型例题
观察下列有规律的数 ….根据其规律,则
(1)第7个数是________;
(2)第n个数是________;
(3) 是第________个数;
(4)计算: .
12
解:(1)由题可知: , , , , ,
(4)解:原式 ,
.
∴ 是第12个数;
(3)根据题意可得: ,
(2)由(1)可得:第n个数是 ;
, 所以第7个数为: ;
②.图形的规律.
典型例题
一张长方形桌子可坐6人,按图3将桌子拼在一起.
(1)2张桌子拼在一起可坐________人,4张桌子拼在一起可坐________人,n张桌子拼在一起可坐________人;
(2)一家餐厅有40张这样的长方形桌子,按照上图的方式每5张拼成1张大桌子,则40张桌子可拼成8张大桌子,共可坐多少人?
(2). (4+2×5)×8=(4+10)×8=14×8=112(人),
n张桌子拼在一起可坐:(4+2n)人;
4张桌子拼在一起可坐:4+2×4=4+8=12(人),
2张桌子拼在一起可坐:4+2×2=4+4=8(人),
解:(1)由图可得,
1. 苹果每千克m元,梨每千克n元购买x千克苹果和y千克梨的用了( ) 元.
(mx+ny)元 B. (nx+my)元
C. mn(x+y)元 D. (m+n)(x+y)元
2. 用式子表示“a 的2倍与b 的的和,结果为( ) .
2a+ b B. (a+b)
C. (2a+b) D. 2(a+ b)
A
A
强化训练
强化训练
3. 下列式子中,是单项式的是( )
A. B. x3yz2 C. D. x y
4. 下列说法不正确的是( )
A. 的系数是
B. 2不是单项式
C. 单项式的次数是2
D. 是多项式
B
B
强化训练
5. 下列各式中:ab, , ab2+b+1,+ , x3+ x2-3中,多项式有( )
A. 2个 B. 3个 C. 4个 D. 5个
6. 下列各式中,不是整式的是( )
A. B. x-y C. D. 4x
B
A
强化训练
7. 下列判断中正确的是( )
是单项式
B. 不是单项式
C. 单项式 和 是同类项
D. +2 + +1 是三次三项式
C
强化训练
8. 若A是一个三次多项式,B是一个四次多项式,则A+B一定是( )
三次多项式
B. 四次多项式或单项式
C. 七次多项式
D. 四次七项式
B
强化训练
10.下列整式运算不正确的是( )
A.
B.
C.
D.
9. 下列各式中,与多项式 相等的是( )
A. B.
C. D.
A
B
强化训练
11. 计算:
(1). 2( 2xy2-x2y) -3(xy+2xy2)-x2y;
(2). a2 -[a2+(3a2 -a) -3(a2 -3a)].
解:(1). 2( 2xy2-x2y) -3(xy+2xy2)-x2y
=( 4xy2-2x2y) -(3xy+6xy2)-x2y
=4xy2-2x2y-3xy-6xy2-x2y
=-3x2y-3xy-2xy2
强化训练
=a2-[a2+3a2 -a -3a2 +9a]
=a2-[a2+8a]
=a2-a2-8a
=-8a
11. 计算:
(1). 2( 2xy2-x2y) -3(xy+2xy2)-x2y;
(2). a2 -[a2+(3a2 -a) -3(a2 -3a)].
解:(2). a2 -[a2+(3a2 -a) -3(a2 -3a)].
强化训练
12. 已知 , .
(1).求 .
(2).当 , 时,求 的值.
解:(1)
解: (2)当 , 时,
;
强化训练
13. 下面是小彬同学进行整式化简的过程,请认真阅读并完成相应任务.
3(3xy﹣x2)﹣2(2x2 xy)
=9xy﹣3x2﹣(4x2 2xy)...........................①
=9xy﹣3x2﹣4x2﹣2xy ..........................②
=7xy﹣7x2 ...................................③
(1):填空:
①以上化简步骤中,第一步的依据是 ;
;②以上化简步骤中,第 步开始出现不符合题意,这一步错误的原因是 .
去括号时,括号前面是号,去掉括号和号,括号内的第二项没有变号
根据乘法分配律
②
解:3(3xy﹣x2)﹣2(2x2 xy)
=9xy﹣3x2﹣(4x2 2xy)
=9xy﹣3x2﹣4x2+2xy
=11xy﹣7x2
当x=-1,y= 时,
原式=11×(-1)×( ) -7×(-1)2=1-7=-6
(2):请写出该整式正确的化简结果,并计算当x=-1,y= 时该整式的值.
强化训练
14. 某医院原有(4m2﹣6m)剂新冠疫苗,上午打了(5m+3)剂,中午休息时又调来(m2+3m)剂,晚上5时发现疫只剩余2(m﹣1)剂.
请问:
(1).该医院中午过后一共打了多少剂新冠疫苗?(用含有m的式子表达)
(2).当m=7时,该医院中午过后一共打了多少剂新冠疫苗?
(1)解:由题意得,
∴该医院中午过后一共打了174剂新冠疫苗.
(2)解:当m=7时,
=
∴该医院中午过后一共打了( )剂新冠疫苗;
=
(4m2﹣6m)-(5m+3)+(m2+3m)-2(m﹣1)
强化训练
(1). 摆第4个图案用________根火柴棒.
(2).按照这种方式摆下去,摆第n个图案用________根火柴棒.
(3). 计算一下摆481根火柴棒时,是第几个图案?
15. 如图是由一些火柴棒搭成的图案.
解:(1)解:由题目得,第①个图案所用的火柴数:
1+4×4=17
第④个图案所用的火柴数:
1+4×3=13
第③个图案所用的火柴数:
1+4×2=9
第②个图案所用的火柴数:
1+4×1=5
强化训练
(2)解:按(1)的方法,依此类推
(3)解:由题意得,
故摆第n个图案用的火柴棒是4n+1
1+4×n=4n+1
第n个图案中,所用的火柴数为:
答:摆481根火柴棒时,是第120个图案.
解得n=120
4n+1=481
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
