辽宁省大连部分重点高中2022-2023学年高二上学期10月月考数学试卷(Word版含解析)
文档属性
| 名称 | 辽宁省大连部分重点高中2022-2023学年高二上学期10月月考数学试卷(Word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-17 19:50:33 | ||
图片预览



文档简介
大连部分重点高中2022-2023学年高二上学期10月月考
数学 试卷
考试时间:120分钟;满分:150分
第Ⅰ卷(选择题)
一、单选题(共40分)
1.已知,,与共线,则( )
A.5 B.6 C.3 D.9
2.若直线的方向向量,平面的法向量,则( )
A. B. C. D.或
3.若构成空间的一组基底,则下列向量不共面的是( )
A.,, B.,,
C.,, D.,,
4.已知、都是空间向量,且,则( )
A. B. C. D.
5.如图,在平行六面体中,与的交点为点,,,,则下列向量中与相等的向量是( )
A. B. C. D.
6.已知大小为60°的二面角棱上有两点、,,,,,若,,,则的长为( )
A.22 B.40 C. D.
7.如图,在边长为3的正方体中,是棱长一点且,是面上的点.一质点从点射向点,遇到正方体的面反射(反射服从光的反射原理),反射到点,则线段与的长度之和为( )
A. B. C. D.
8.如图,在三棱柱中,侧棱底面,,,是棱的中点,是的延长线与的延长线的交点.若点在直线上,则下列结论正确的是( )
A.当点为线段的中点时,平面
B.当点为线段的三等分点时,平面
C.在线段的延长线上,存在一点,使得平面
D.不存在点,使与平面垂直
二、多选题(共20分)
9.已知空间中三点,,,则下列说法正确的是( )
A.与是共线向量 B.与同向的单位向量是
C.和夹角的余弦值是 D.平面的一个法向量是
10.过所在平面外一点,作,垂足为,以下推断正确的是( )
A.若,,则点是的垂心
B.若,则点是的外心
C.若,,则点是的内心
D.过点分别作边,,的垂线,垂足分别为,,,若,则点是的重心
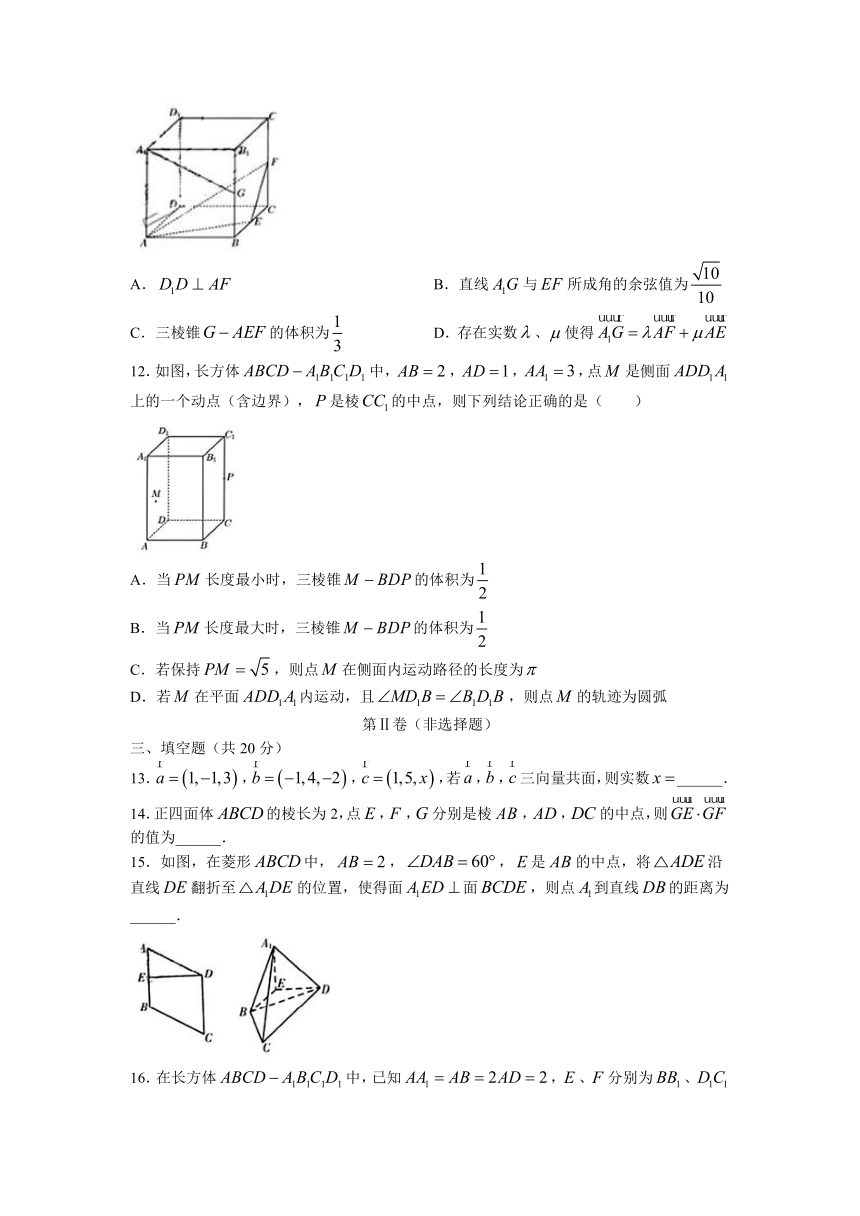
11.在棱长为2的正方体中,、、分别为、、的中点,则下列选项正确的是( )
A. B.直线与所成角的余弦值为
C.三棱锥的体积为 D.存在实数、使得
12.如图,长方体中,,,,点是侧面上的一个动点(含边界),是棱的中点,则下列结论正确的是( )
A.当长度最小时,三棱锥的体积为
B.当长度最大时,三棱锥的体积为
C.若保持,则点在侧面内运动路径的长度为
D.若在平面内运动,且,则点的轨迹为圆弧
第Ⅱ卷(非选择题)
三、填空题(共20分)
13.,,,若,,三向量共面,则实数______.
14.正四面体的棱长为2,点,,分别是棱,,的中点,则的值为______.
15.如图,在菱形中,,,是的中点,将沿直线翻折至的位置,使得面面,则点到直线的距离为______.
16.在长方体中,已知,、分别为、的中点,则三棱锥的外接球半径为______,平面被三棱锥外接球截得的截面圆面积为______.
四、解答题(共60分)
17.(1)已知,,且,求,的值;
(2)已知,,若与(为坐标原点)的夹角为60°,求的值.
18.如图,在三棱锥中,平面,,,点,分别是,的中点.
(1)求证:平面;
(2)设,求直线与平面所成角的正弦值
19.如图所示,在四棱锥中,为等腰直角三角形,且,四边形为直角梯形,满足,,,.
(1)若点为的中点,求;
(2)若点为的中点,点为上一点,当时,求的值.
20.在①,②,③这三个条件中任选一个,补充在下面的问题中,并作答.
问题:如图,在正方体中,以为坐标原点,建立空间直角坐标系.已知点的坐标为,为棱上的动点,为棱上的动点,______,则是否存在点,,使得?若存在,求出的值;若不存在,请说明理由.
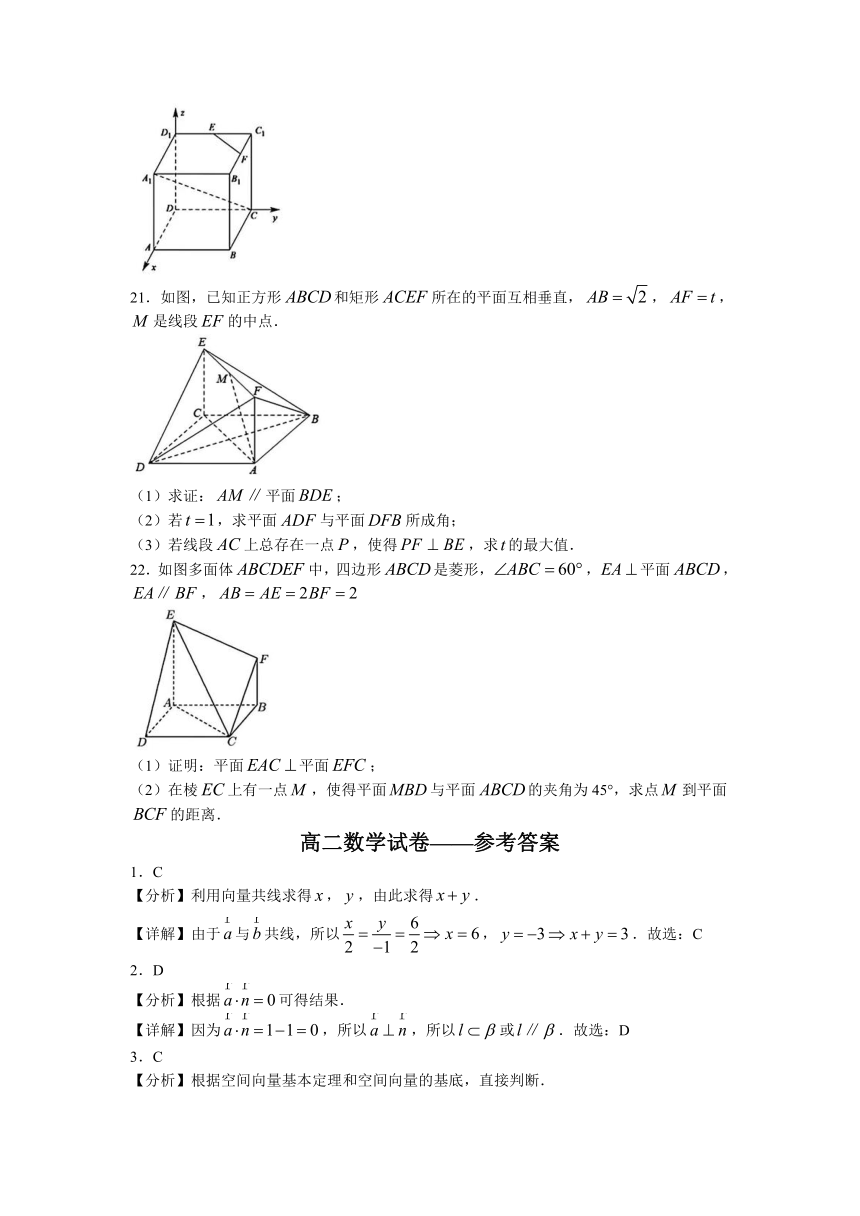
21.如图,已知正方形和矩形所在的平面互相垂直,,,是线段的中点.
(1)求证:平面;
(2)若,求平面与平面所成角;
(3)若线段上总存在一点,使得,求的最大值.
22.如图多面体中,四边形是菱形,,平面,,
(1)证明:平面平面;
(2)在棱上有一点,使得平面与平面的夹角为45°,求点到平面的距离.
高二数学试卷——参考答案
1.C
【分析】利用向量共线求得,,由此求得.
【详解】由于与共线,所以,.故选:C
2.D
【分析】根据可得结果.
【详解】因为,所以,所以或.故选:D
3.C
【分析】根据空间向量基本定理和空间向量的基底,直接判断.
【详解】选项A:,所以,,共面;
选项B:,所以,,共面;
选项C:不能用,表示,所以,,不共面;
选项D:,共线,则,,共面.故选:C
4.A
【分析】利用空间向量的数量积运算即可得到答案
【详解】解:∵,∴,
∴,∵,∴,故选:A
5.C
【分析】根据空间向量的线性运算用,,表示出即可得.
【详解】.故选:C.
6.C
【分析】过作且,连接、,易得,通过线面垂直的判定定理可得平面,继而得到,即可求出答案
【详解】解:过作且,连接、,则四边形是平行四边形,
因为,所以平行四边形是矩形,
因为,即,而,
则是二面角的平面角,即,
因为,即为正三角形,所以,
因为,即,,,平面,
所以平面,因为平面,所以,
所以在中,,所以
故选:C
7.C
【分析】以点为坐标原点,、、所在直线分别为、、轴建立空间直角坐标系,作点关于平面的对称点,计算出即可.
【详解】以点为坐标原点,、、所在直线分别为、、轴建立如下图所示的空间直角坐标系,则、,
作点关于平面的对称点,由对称性可知,且、、三点共线,
故.故选:C.
8.D
【解析】本题就是研究在直线上有没有点使得平面,我们就由平面出发推导发现结论或矛盾.
【详解】是棱的中点,是的延长线与的延长线的交点,由于,∴是中点,以,,为,,轴建立空间直角坐标系,如图,则,,,,,,,
在坐标平面上,直线方程为,即,在直线上,设,则,又,,若平面,则,,∴,,,与矛盾,∴直线上不存在点,使与平面垂直.故选:D.
【点睛】本题考查线面垂直的判断与性质.解题关键是建立空间直角坐标系,把线面垂直所得线线垂直转化为向量垂直,利用向量的数量积计算.简化了问题的求解.本题也可用三垂线定理及其逆定理分析.
9.BD
【分析】根据共线向量的坐标显示可知A错误;根据与同向的单位向量为,计算可知B正确;
利用向量夹角公式计算可知C错误;根据法向量的求法可知D正确.
【详解】对于A,,,可知,与不共线,A错误;
对于B,∵,∴,∴,即与同向的单位向量是,B正确;
对于C,∵,∴,
即和夹角的余弦值为,C错误;
对于D,设平面的法向量,
则,令,解得:,,∴,
即平面的一个法向量为,D正确.故选:BD.
10.ABC
【分析】对于A选项,由题意得出,,点是的垂心;
对于B选项,若,则,点是的外心;
对于C选项,由题意得出是的平分线,是的平分线,点是的内心;
对于D选项,若,则,进而结合C选项的讨论得点是的内心.
【详解】对于A,∵底面,,底面,∴,
又,,,,平面,,,平面∴平面,平面,
∵平面,平面,∴;,
∴点是的垂心,A选项正确;
对于B,若,则,
∴,点是的外心,B选项正确;
对于C,过点分别作边,,的垂线,垂足分别为,,,
若,则,,
∵底面,,底面,∴,,
∴,∴,∴,即是的平分线,
同理时,是的平分线,∴点是的内心,故C选项正确;
对于D,过点分别作边,,的垂线,垂足分别为,,,
若,则,结合C选项的讨论可知,点是的内心,D选项错误.
故选:ABC.
11.BD
【分析】对于A,根据平行线的与已知直线的垂直关系,可得答案;
对于B,根据线线夹角的定义,作平行,根据三角形的余弦定理,可得答案;
对于C,根据体积的组合关系,找到三棱锥所在的三棱柱,减去其余部分,可得答案;
对于D,根据平行关系,进行平面延拓,由线面平行,可得三个向量共面,可得答案.
【详解】对于A,在正方体中,,易知与不垂直,故错误;
对于B,在正方体中,取的中点,连接,,如下图,
易知,则为直线与夹角或其补角,∵,∴,,在中,,因此,直线与所成角的余弦值为,故正确;
对于C,根据题意作图如下:
易知三棱柱的体积,
三棱锥的体积,
四棱锥的体积,
三棱锥的体积,故错误;
对于D,连接,,作图如下:
易知,则,,,共面,∵,则,,共面,
即存在实数、使得,故正确;故选:BD.
12.ABC
【分析】由等体积法可判断AB正确,由圆的知识可判断C正确,利用空间向量法求夹角余弦值,可知D错误.
【详解】对于A,当长度最小时,点在线段的中点,
,,A正确.
对于B,当长度最大时,点与点或点重合,若点与点重合,
,B正确.
对于C,作中点,连接,,如下图所示,易证平面,
平面,则,若保持,则,
则点的轨迹是以1为半径的半圆弧,长度为,C正确.
对于D,以点为原点建立空间直角坐标系如图所示:
则,,,设,
则有,,,
若,则有,即,
化简得:,即,
即或(此时,,),
故点的轨迹为一段直线,D错误.故选:ABC
13.5
【分析】根据空间向量共面列出方程组,求出.
【详解】,,,若,,三向量共面,
设,即,
所以,解得:,所以.故答案为:5
14.1
【分析】根据给定条件用空间向量的一个基底表示与,再利用空间向量数量积及运算律计算作答.
【详解】在正四面体中,令,,,显然,,,如图:
因点,,分别是棱,,的中点,则,
,
于是得,
所以的值为1.故答案为:1
15.
【分析】利用菱形的性质可得,结合面面垂直的性质定理可得平面,,进一步得到,并计算,最后利用勾股定理可得结果.
【详解】解:在菱形中,,,所以是边长为2的等边三角形,
又因为为的中点,所以,又面面,面面,
平面,所以平面,
作交于点,由,,,平面
所以平面,所以
,所以故答案为:
16. ##
【分析】建立空间直角坐标系,利用向量坐标,可以证明,取为中点,有,因此点为三棱锥外接球的球心,则,球心到平面的距离为,勾股定理可得截面圆的半径为,即得解
【详解】解:以点为原点建立空间直角坐标系如图所示:
依题意得:,,,则,,
所以,则即;
设为中点,因为,,则,
所以点为三棱锥外接球的球心,则三棱锥外接球的半径为,
设球心到平面的距离为,又因为为中点,所以点到平面的距离为,
由于,所以,
故截面圆的半径为,所以截面圆面积为,故答案为:;
17.(1),;(2)
【分析】(1)利用空间向量的坐标运算,结合空间向量共线的坐标表示计算作答;
(2)先算出,,然后利用数量积的坐标运算得到,再利用夹角公式即可得到答案
【详解】(1)因为,,
所以,,
因为,所以,解得,,所以,;
(2)因为,,所以,,
所以,因为与的夹角为60°,
所以,因为,解得
18.(1)证明见解析,(2)
【分析】(1)由平面,可得,由可得,然后由线面垂直的判定定理可结论.
(2)如图建立空间直角坐标系,利用空间向量求解即可
【详解】(1)证明:因为平面,平面,所以,
因为,所以,因为,所以平面;
(2)解:因为平面,平面,所以,
所以,,两两垂直,所以以为原点,分别以,,为,,轴建立空间直角坐标系,如图所示,则,,,,则,
因为点,分别是,的中点,所以,,所以,,
设平面的一个法向量为,则
,令,则,直线与平面所成角为,则
,所以直线与平面所成角的正弦值为
19.(1)(2)
【分析】(1)可证,再建立如图所示的空间直角坐标系,求出,的坐标后可求夹角的余弦值.
(2)设,则可用表示的坐标,再利用可求,从而可得两条线段的比值.
(1)因为为等腰直角三角形,,,所以,
又,,所以.而,,故,因,,平面,故平面.以点为原点,,所在直线分别为,轴,过点作的平行线为轴,建立空间直角坐标系,如图所示.
则,,,,.
则,,
所以.
(2)由(1)知,设,
而,所以,
所以,所以,又,
因为,故,所以,解得,
所以.
20.答案见解析
【分析】根据空间直角坐标系中点的坐标可得向量的坐标,由向量的坐标运算可计算模长以及数量积,进而可求解.
【详解】方案一:选条件①.
假设存在满足题意的点,.由题意,知正方体的棱长为2,则,,,,,所以.设,,则,
,,所以,.
因为,所以,即.
因为,,所以,所以.又,
所以,故存在点,,满足,此时.
方案二:选条件②.
假设存在满足题意的点,.由题意,知正方体的棱长为2,则,,,,,所以.
设,,则,,,
所以,.因为,且,
所以,解得.又,所以,
故存在点,,满足,此时.
方案三:选条件③.假设存在满足题意的点,.由题意,知正方体的棱长为2,
则,,,,所以,.
设,,则.因为,
所以与不共线,所以,即,则,故不存在点,满足.
21.(1)证明见解析(2)(3)
【分析】(1)设,连接,进而证明即可证明结论;
(2)根据题意平面,进而以为轴,为轴,为轴,建立如图所示空间直角坐标系,利用坐标法求解即可;
(3)设,其中,进而结合题意得,再求解即可.
(1)证明:设,连接,
因为矩形中是线段的中点,是线段的中点,
所以,,所以为平行四边形,所以,又平面,平面,所以平面;
(2)解:由题意,正方形和矩形所在的平面互相垂直,
因为平面平面,,所以平面,
所以,以为轴,为轴,为轴,建立如图所示空间直角坐标系,
若,则,,,则,,
可知平面的一个法向量为,设平面的法向量为,
则由,可知,不妨令,则,,即,
设平面与平面所成角为,因为为锐角,所以,
所以平面与平面所成角的大小为.
(3)解:,,,则,
因为点在线段上,设,其中,
则,从而点坐标为,
于是,而,
则由可知,即,
所以,解得,故的最大值为
22.(1)证明见解析(2)
【分析】(1)取的中点,连接交于,连接,,证明,利用平面,证明平面,从而平面平面;
(2)建立平面直角坐标系,设,求出二面角,再求得的值,即可得到的坐标,再利用空间向量法求出点到面的距离.
(1)证明:取的中点,连接交于,连接,,
因为是菱形,所以,且是的中点,
所以且,又,,
所以且,所以四边形是平行四边形,所以,
又平面,平面,所以,
又因为,,平面,
所以平面,所以平面,
又平面,所以平面平面;
(2)解:取的中点,由四边形是菱形,,则,
∴是正三角形,∴,∴,又平面,
所以以为原点,,,为坐标轴建立空间直角坐标系,
设在棱上存在点使得平面与平面的夹角为45°,
则,,,,,,
则设,∴,
所以,,,,
设平面的一个法向量为,
则,即,令,,得
平面的法向量可以为,
∴,解得,
所以,则
设平面的一个法向量为,
则,即,取,得,
所以点到平面的距离.
数学 试卷
考试时间:120分钟;满分:150分
第Ⅰ卷(选择题)
一、单选题(共40分)
1.已知,,与共线,则( )
A.5 B.6 C.3 D.9
2.若直线的方向向量,平面的法向量,则( )
A. B. C. D.或
3.若构成空间的一组基底,则下列向量不共面的是( )
A.,, B.,,
C.,, D.,,
4.已知、都是空间向量,且,则( )
A. B. C. D.
5.如图,在平行六面体中,与的交点为点,,,,则下列向量中与相等的向量是( )
A. B. C. D.
6.已知大小为60°的二面角棱上有两点、,,,,,若,,,则的长为( )
A.22 B.40 C. D.
7.如图,在边长为3的正方体中,是棱长一点且,是面上的点.一质点从点射向点,遇到正方体的面反射(反射服从光的反射原理),反射到点,则线段与的长度之和为( )
A. B. C. D.
8.如图,在三棱柱中,侧棱底面,,,是棱的中点,是的延长线与的延长线的交点.若点在直线上,则下列结论正确的是( )
A.当点为线段的中点时,平面
B.当点为线段的三等分点时,平面
C.在线段的延长线上,存在一点,使得平面
D.不存在点,使与平面垂直
二、多选题(共20分)
9.已知空间中三点,,,则下列说法正确的是( )
A.与是共线向量 B.与同向的单位向量是
C.和夹角的余弦值是 D.平面的一个法向量是
10.过所在平面外一点,作,垂足为,以下推断正确的是( )
A.若,,则点是的垂心
B.若,则点是的外心
C.若,,则点是的内心
D.过点分别作边,,的垂线,垂足分别为,,,若,则点是的重心
11.在棱长为2的正方体中,、、分别为、、的中点,则下列选项正确的是( )
A. B.直线与所成角的余弦值为
C.三棱锥的体积为 D.存在实数、使得
12.如图,长方体中,,,,点是侧面上的一个动点(含边界),是棱的中点,则下列结论正确的是( )
A.当长度最小时,三棱锥的体积为
B.当长度最大时,三棱锥的体积为
C.若保持,则点在侧面内运动路径的长度为
D.若在平面内运动,且,则点的轨迹为圆弧
第Ⅱ卷(非选择题)
三、填空题(共20分)
13.,,,若,,三向量共面,则实数______.
14.正四面体的棱长为2,点,,分别是棱,,的中点,则的值为______.
15.如图,在菱形中,,,是的中点,将沿直线翻折至的位置,使得面面,则点到直线的距离为______.
16.在长方体中,已知,、分别为、的中点,则三棱锥的外接球半径为______,平面被三棱锥外接球截得的截面圆面积为______.
四、解答题(共60分)
17.(1)已知,,且,求,的值;
(2)已知,,若与(为坐标原点)的夹角为60°,求的值.
18.如图,在三棱锥中,平面,,,点,分别是,的中点.
(1)求证:平面;
(2)设,求直线与平面所成角的正弦值
19.如图所示,在四棱锥中,为等腰直角三角形,且,四边形为直角梯形,满足,,,.
(1)若点为的中点,求;
(2)若点为的中点,点为上一点,当时,求的值.
20.在①,②,③这三个条件中任选一个,补充在下面的问题中,并作答.
问题:如图,在正方体中,以为坐标原点,建立空间直角坐标系.已知点的坐标为,为棱上的动点,为棱上的动点,______,则是否存在点,,使得?若存在,求出的值;若不存在,请说明理由.
21.如图,已知正方形和矩形所在的平面互相垂直,,,是线段的中点.
(1)求证:平面;
(2)若,求平面与平面所成角;
(3)若线段上总存在一点,使得,求的最大值.
22.如图多面体中,四边形是菱形,,平面,,
(1)证明:平面平面;
(2)在棱上有一点,使得平面与平面的夹角为45°,求点到平面的距离.
高二数学试卷——参考答案
1.C
【分析】利用向量共线求得,,由此求得.
【详解】由于与共线,所以,.故选:C
2.D
【分析】根据可得结果.
【详解】因为,所以,所以或.故选:D
3.C
【分析】根据空间向量基本定理和空间向量的基底,直接判断.
【详解】选项A:,所以,,共面;
选项B:,所以,,共面;
选项C:不能用,表示,所以,,不共面;
选项D:,共线,则,,共面.故选:C
4.A
【分析】利用空间向量的数量积运算即可得到答案
【详解】解:∵,∴,
∴,∵,∴,故选:A
5.C
【分析】根据空间向量的线性运算用,,表示出即可得.
【详解】.故选:C.
6.C
【分析】过作且,连接、,易得,通过线面垂直的判定定理可得平面,继而得到,即可求出答案
【详解】解:过作且,连接、,则四边形是平行四边形,
因为,所以平行四边形是矩形,
因为,即,而,
则是二面角的平面角,即,
因为,即为正三角形,所以,
因为,即,,,平面,
所以平面,因为平面,所以,
所以在中,,所以
故选:C
7.C
【分析】以点为坐标原点,、、所在直线分别为、、轴建立空间直角坐标系,作点关于平面的对称点,计算出即可.
【详解】以点为坐标原点,、、所在直线分别为、、轴建立如下图所示的空间直角坐标系,则、,
作点关于平面的对称点,由对称性可知,且、、三点共线,
故.故选:C.
8.D
【解析】本题就是研究在直线上有没有点使得平面,我们就由平面出发推导发现结论或矛盾.
【详解】是棱的中点,是的延长线与的延长线的交点,由于,∴是中点,以,,为,,轴建立空间直角坐标系,如图,则,,,,,,,
在坐标平面上,直线方程为,即,在直线上,设,则,又,,若平面,则,,∴,,,与矛盾,∴直线上不存在点,使与平面垂直.故选:D.
【点睛】本题考查线面垂直的判断与性质.解题关键是建立空间直角坐标系,把线面垂直所得线线垂直转化为向量垂直,利用向量的数量积计算.简化了问题的求解.本题也可用三垂线定理及其逆定理分析.
9.BD
【分析】根据共线向量的坐标显示可知A错误;根据与同向的单位向量为,计算可知B正确;
利用向量夹角公式计算可知C错误;根据法向量的求法可知D正确.
【详解】对于A,,,可知,与不共线,A错误;
对于B,∵,∴,∴,即与同向的单位向量是,B正确;
对于C,∵,∴,
即和夹角的余弦值为,C错误;
对于D,设平面的法向量,
则,令,解得:,,∴,
即平面的一个法向量为,D正确.故选:BD.
10.ABC
【分析】对于A选项,由题意得出,,点是的垂心;
对于B选项,若,则,点是的外心;
对于C选项,由题意得出是的平分线,是的平分线,点是的内心;
对于D选项,若,则,进而结合C选项的讨论得点是的内心.
【详解】对于A,∵底面,,底面,∴,
又,,,,平面,,,平面∴平面,平面,
∵平面,平面,∴;,
∴点是的垂心,A选项正确;
对于B,若,则,
∴,点是的外心,B选项正确;
对于C,过点分别作边,,的垂线,垂足分别为,,,
若,则,,
∵底面,,底面,∴,,
∴,∴,∴,即是的平分线,
同理时,是的平分线,∴点是的内心,故C选项正确;
对于D,过点分别作边,,的垂线,垂足分别为,,,
若,则,结合C选项的讨论可知,点是的内心,D选项错误.
故选:ABC.
11.BD
【分析】对于A,根据平行线的与已知直线的垂直关系,可得答案;
对于B,根据线线夹角的定义,作平行,根据三角形的余弦定理,可得答案;
对于C,根据体积的组合关系,找到三棱锥所在的三棱柱,减去其余部分,可得答案;
对于D,根据平行关系,进行平面延拓,由线面平行,可得三个向量共面,可得答案.
【详解】对于A,在正方体中,,易知与不垂直,故错误;
对于B,在正方体中,取的中点,连接,,如下图,
易知,则为直线与夹角或其补角,∵,∴,,在中,,因此,直线与所成角的余弦值为,故正确;
对于C,根据题意作图如下:
易知三棱柱的体积,
三棱锥的体积,
四棱锥的体积,
三棱锥的体积,故错误;
对于D,连接,,作图如下:
易知,则,,,共面,∵,则,,共面,
即存在实数、使得,故正确;故选:BD.
12.ABC
【分析】由等体积法可判断AB正确,由圆的知识可判断C正确,利用空间向量法求夹角余弦值,可知D错误.
【详解】对于A,当长度最小时,点在线段的中点,
,,A正确.
对于B,当长度最大时,点与点或点重合,若点与点重合,
,B正确.
对于C,作中点,连接,,如下图所示,易证平面,
平面,则,若保持,则,
则点的轨迹是以1为半径的半圆弧,长度为,C正确.
对于D,以点为原点建立空间直角坐标系如图所示:
则,,,设,
则有,,,
若,则有,即,
化简得:,即,
即或(此时,,),
故点的轨迹为一段直线,D错误.故选:ABC
13.5
【分析】根据空间向量共面列出方程组,求出.
【详解】,,,若,,三向量共面,
设,即,
所以,解得:,所以.故答案为:5
14.1
【分析】根据给定条件用空间向量的一个基底表示与,再利用空间向量数量积及运算律计算作答.
【详解】在正四面体中,令,,,显然,,,如图:
因点,,分别是棱,,的中点,则,
,
于是得,
所以的值为1.故答案为:1
15.
【分析】利用菱形的性质可得,结合面面垂直的性质定理可得平面,,进一步得到,并计算,最后利用勾股定理可得结果.
【详解】解:在菱形中,,,所以是边长为2的等边三角形,
又因为为的中点,所以,又面面,面面,
平面,所以平面,
作交于点,由,,,平面
所以平面,所以
,所以故答案为:
16. ##
【分析】建立空间直角坐标系,利用向量坐标,可以证明,取为中点,有,因此点为三棱锥外接球的球心,则,球心到平面的距离为,勾股定理可得截面圆的半径为,即得解
【详解】解:以点为原点建立空间直角坐标系如图所示:
依题意得:,,,则,,
所以,则即;
设为中点,因为,,则,
所以点为三棱锥外接球的球心,则三棱锥外接球的半径为,
设球心到平面的距离为,又因为为中点,所以点到平面的距离为,
由于,所以,
故截面圆的半径为,所以截面圆面积为,故答案为:;
17.(1),;(2)
【分析】(1)利用空间向量的坐标运算,结合空间向量共线的坐标表示计算作答;
(2)先算出,,然后利用数量积的坐标运算得到,再利用夹角公式即可得到答案
【详解】(1)因为,,
所以,,
因为,所以,解得,,所以,;
(2)因为,,所以,,
所以,因为与的夹角为60°,
所以,因为,解得
18.(1)证明见解析,(2)
【分析】(1)由平面,可得,由可得,然后由线面垂直的判定定理可结论.
(2)如图建立空间直角坐标系,利用空间向量求解即可
【详解】(1)证明:因为平面,平面,所以,
因为,所以,因为,所以平面;
(2)解:因为平面,平面,所以,
所以,,两两垂直,所以以为原点,分别以,,为,,轴建立空间直角坐标系,如图所示,则,,,,则,
因为点,分别是,的中点,所以,,所以,,
设平面的一个法向量为,则
,令,则,直线与平面所成角为,则
,所以直线与平面所成角的正弦值为
19.(1)(2)
【分析】(1)可证,再建立如图所示的空间直角坐标系,求出,的坐标后可求夹角的余弦值.
(2)设,则可用表示的坐标,再利用可求,从而可得两条线段的比值.
(1)因为为等腰直角三角形,,,所以,
又,,所以.而,,故,因,,平面,故平面.以点为原点,,所在直线分别为,轴,过点作的平行线为轴,建立空间直角坐标系,如图所示.
则,,,,.
则,,
所以.
(2)由(1)知,设,
而,所以,
所以,所以,又,
因为,故,所以,解得,
所以.
20.答案见解析
【分析】根据空间直角坐标系中点的坐标可得向量的坐标,由向量的坐标运算可计算模长以及数量积,进而可求解.
【详解】方案一:选条件①.
假设存在满足题意的点,.由题意,知正方体的棱长为2,则,,,,,所以.设,,则,
,,所以,.
因为,所以,即.
因为,,所以,所以.又,
所以,故存在点,,满足,此时.
方案二:选条件②.
假设存在满足题意的点,.由题意,知正方体的棱长为2,则,,,,,所以.
设,,则,,,
所以,.因为,且,
所以,解得.又,所以,
故存在点,,满足,此时.
方案三:选条件③.假设存在满足题意的点,.由题意,知正方体的棱长为2,
则,,,,所以,.
设,,则.因为,
所以与不共线,所以,即,则,故不存在点,满足.
21.(1)证明见解析(2)(3)
【分析】(1)设,连接,进而证明即可证明结论;
(2)根据题意平面,进而以为轴,为轴,为轴,建立如图所示空间直角坐标系,利用坐标法求解即可;
(3)设,其中,进而结合题意得,再求解即可.
(1)证明:设,连接,
因为矩形中是线段的中点,是线段的中点,
所以,,所以为平行四边形,所以,又平面,平面,所以平面;
(2)解:由题意,正方形和矩形所在的平面互相垂直,
因为平面平面,,所以平面,
所以,以为轴,为轴,为轴,建立如图所示空间直角坐标系,
若,则,,,则,,
可知平面的一个法向量为,设平面的法向量为,
则由,可知,不妨令,则,,即,
设平面与平面所成角为,因为为锐角,所以,
所以平面与平面所成角的大小为.
(3)解:,,,则,
因为点在线段上,设,其中,
则,从而点坐标为,
于是,而,
则由可知,即,
所以,解得,故的最大值为
22.(1)证明见解析(2)
【分析】(1)取的中点,连接交于,连接,,证明,利用平面,证明平面,从而平面平面;
(2)建立平面直角坐标系,设,求出二面角,再求得的值,即可得到的坐标,再利用空间向量法求出点到面的距离.
(1)证明:取的中点,连接交于,连接,,
因为是菱形,所以,且是的中点,
所以且,又,,
所以且,所以四边形是平行四边形,所以,
又平面,平面,所以,
又因为,,平面,
所以平面,所以平面,
又平面,所以平面平面;
(2)解:取的中点,由四边形是菱形,,则,
∴是正三角形,∴,∴,又平面,
所以以为原点,,,为坐标轴建立空间直角坐标系,
设在棱上存在点使得平面与平面的夹角为45°,
则,,,,,,
则设,∴,
所以,,,,
设平面的一个法向量为,
则,即,令,,得
平面的法向量可以为,
∴,解得,
所以,则
设平面的一个法向量为,
则,即,取,得,
所以点到平面的距离.
同课章节目录
