初中数学人教版九年级上册24.2.1点和圆的位置关系 学案(含答案)
文档属性
| 名称 | 初中数学人教版九年级上册24.2.1点和圆的位置关系 学案(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 367.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-17 15:34:45 | ||
图片预览



文档简介
第二十四章 圆
24.2.1点和圆的位置关系
学案
一、学习目标
1.理解点和圆的三种位置关系及判定方法,能熟练地运用判定方法判定点与圆的位置关系.
2.掌握不在同一条直线上的三点确定一个圆,能画出三角形的外接圆.
二、基础知识
点和圆的位置关系:
①观察图中点A,B,C与圆的位置关系.
②设的半径为r,请说出点A,B,C与圆心O的距离与半径的关系.
③反过来,已知点到圆心的距离和圆的半径,能否判断点和圆的位置关系?
探究(确定圆的条件):
①我们知道,已知圆心和半径,可以作一个圆.经过一个已知点A能不能作圆,这样的圆你能作出多少个?
②经过两个已知点A,B能不能作圆?如果能,圆心分布有什么特点?
③经过不在同一条直线上的三个点A,B,C能不能作圆?如果能,如何确定所作圆的圆心?
三角形的外接圆:
①一个圆可以有 个内接三角形,但是一个三角形 个外接圆
②三角形的外心到三角形三个顶点的距离相等,等于 .
③三角形外心的位置:锐角三角形的外心在三角形的 ;直角三角形的外心是 ;钝角三角形的外心在三角形的 .
反证法:
①定义:____________________________________________________________
___________________________
及时练(判断题)
1.过三点一定可以作圆
2.三角形有且只有一个外接圆
3.任意一个圆有一个内接三角形,并且只有一个内接三角形
4.三角形的外心就是这个三角形任意两条垂直平分线的交点
5.三角形的外心到三边的距离相等
三、巩固练习
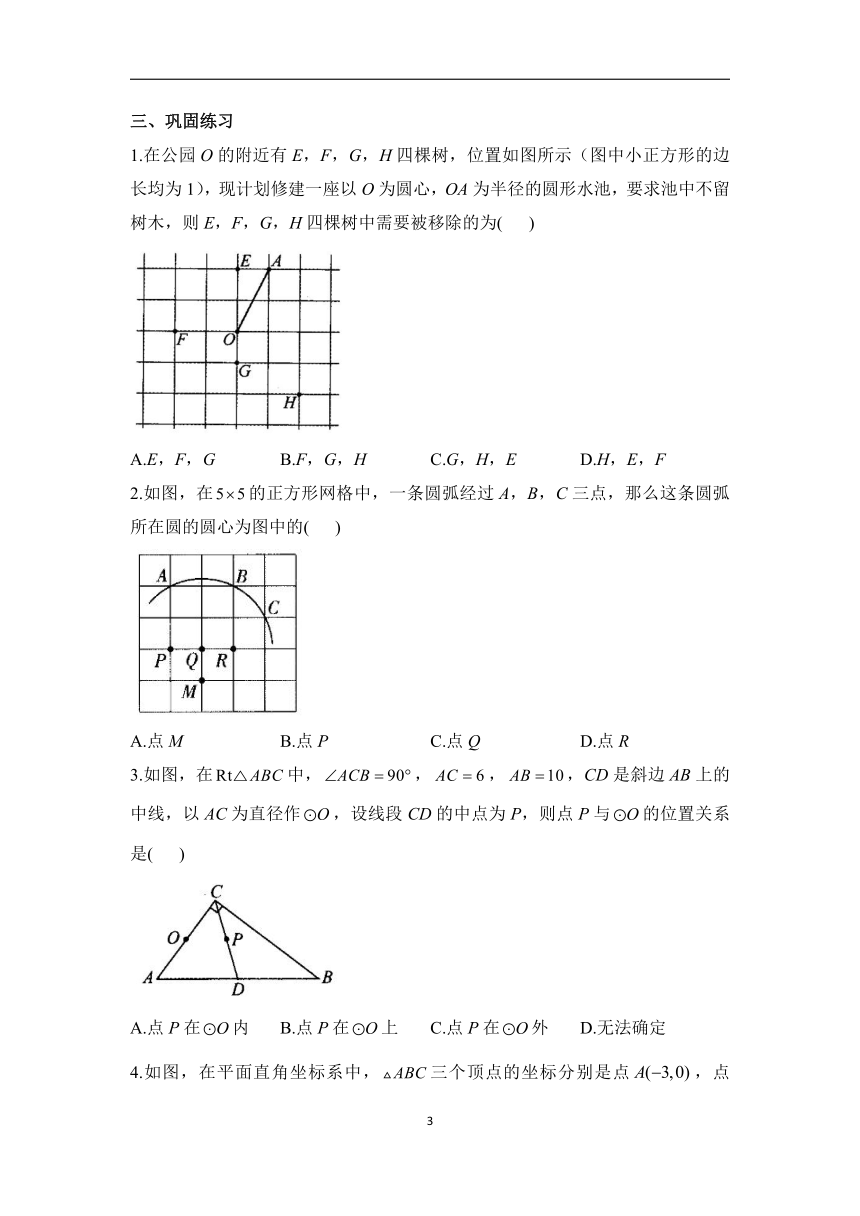
1.在公园O的附近有E,F,G,H四棵树,位置如图所示(图中小正方形的边长均为1),现计划修建一座以O为圆心,OA为半径的圆形水池,要求池中不留树木,则E,F,G,H四棵树中需要被移除的为( )
A.E,F,G B.F,G,H C.G,H,E D.H,E,F
2.如图,在的正方形网格中,一条圆弧经过A,B,C三点,那么这条圆弧所在圆的圆心为图中的( )
A.点M B.点P C.点Q D.点R
3.如图,在中,,,,CD是斜边AB上的中线,以AC为直径作,设线段CD的中点为P,则点P与的位置关系是( )
A.点P在内 B.点P在上 C.点P在外 D.无法确定
4.如图,在平面直角坐标系中,三个顶点的坐标分别是点,点,点,则的外心的坐标是( )
A. B. C. D.
5.利用反证法证明:“直角三角形至少有一个锐角不小于”时,应先假设( )
A.直角三角形的每个锐角都小于
B.直角三角形有一个锐角大于
C.直角三角形的每个锐角都大于
D.直角三角形有一个锐角小于
6.如图,在中,,,,以点C为圆心,以r为半径作圆,请回答下列问题.
(1)当r取何值时,点A在上,且点B在内部?
(2)当r在什么范围内取值时,点A在外部,且点B在内部?
(3)是否存在这样的实数r,使得点B在上,且点A在内部?
7.如图,圆O是的外接圆,AO平分.
(1)求证:是等腰三角形;
(2)若,,求边BC的长.
8.用反证法证明“等腰三角形的底角都是锐角”.
答案
基础知识
点和圆的位置关系:
①点和圆的三种位置关系:点在圆上,点在圆外,点在圆内.
②OAr,由位置关系得出数量关系.
③点P在圆内;点P在圆上;点P在圆外,由数量关系得出位置关系.
探究(确定圆的条件):
①经过一个点A作圆,只要以点A以外任意一点为圆心,以这一点与点A的距离为半径就可以作出,这样的圆有无数个,如下图(1).
②经过两点A,B作圆,由于所作圆的圆心到A,B两点的距离相等,所以圆心在线段AB的垂直平分线,这样的圆也可以作出无数个,如下图(2).
③如图,三点A,B,C不在同一条直线上,因为所求的圆要经过A,B,C三点,所以圆心到这三点的距离相等,因此这个点要在线段AB的垂直平分线上,又要在线段BC的垂直平分线上.
(1)分别连接AB,BC,AC;
(2)分别作线段AB,BC的垂直平分线l1和l2,设它们的交点为O,则OA=OB=OC;
(3)以点O为圆心,OA(或OB,OC)为半径作圆,便可以作经过A,B,C三点的圆.
因为过ABC三点的圆的圆心只能是点O,半径等于OA,所以这样的圆只能有一个,即:不在同一条直线上的三点确定一个圆.
三角形的外接圆:
①无数;只有一
②其外接圆的半径
③内部;斜边的中点;外部
反证法:
①假设命题的结论不成立,由此经过推理得出矛盾,由矛盾断定所作假设不正确,从而得到原命题成立.
及时练(判断题)
答案:1.× 2.√ 3.× 4.√ 5.×
巩固练习
1.答案:A
解析:结合网格图可知,,,,,所以E,F,G,H四棵树中需要被移除的为E,F,G,故选A.
2.答案:C
解析:分别作线段AB和BC的垂直平分线,发现它们都经过点Q,所以点Q为这条圆弧所在圆的圆心.故选C.
3.答案:A
解析:在中,,,,O是AC的中点,P是CD的中点,所以OP是的中位线,且.又因为半径,,所以点P在内.
4.答案:D
解析:设点P是的外心.点P到的三个顶点的距离相等,点P是线段BC,AB的垂直平分线的交点.由图可知,点P的坐标为.故选D.
5.答案:A
解析:用反证法证明命题“在直角三角形中,至少有一个锐角不小于”时,应先假设直角三角形的每个锐角都小于.
故选:A.
6.答案:(1)当时,点A在上,且点B在内部
(2)当时,点A在外部,且点B在内部
(3)不存在这样的实数r,使得点B在上,且点A在内部
解析:(1)在中,,,,
.
当时,点A在上,且点B在内部.
(2)当时,点A在外部,且点B在内部.
(3)不存在这样的实数r,使得点B在上,且点A在内部.
7.答案:(1)见解析
(2)
解析:(1)如图,连接OB,OC.
,AO平分,
.
在和中,
,,
是等腰三角形.
(2)如图,延长AO交BC于点H.
平分,,,.
设,.,,,,
解得
.
8.答案:已知:在中,.
求证:都是锐角.
证明:假设都是直角或钝角,
,
,
,
这与三角形内角和为180°矛盾.
假设不成立,原命题的结论正确,
即都是锐角.
2
24.2.1点和圆的位置关系
学案
一、学习目标
1.理解点和圆的三种位置关系及判定方法,能熟练地运用判定方法判定点与圆的位置关系.
2.掌握不在同一条直线上的三点确定一个圆,能画出三角形的外接圆.
二、基础知识
点和圆的位置关系:
①观察图中点A,B,C与圆的位置关系.
②设的半径为r,请说出点A,B,C与圆心O的距离与半径的关系.
③反过来,已知点到圆心的距离和圆的半径,能否判断点和圆的位置关系?
探究(确定圆的条件):
①我们知道,已知圆心和半径,可以作一个圆.经过一个已知点A能不能作圆,这样的圆你能作出多少个?
②经过两个已知点A,B能不能作圆?如果能,圆心分布有什么特点?
③经过不在同一条直线上的三个点A,B,C能不能作圆?如果能,如何确定所作圆的圆心?
三角形的外接圆:
①一个圆可以有 个内接三角形,但是一个三角形 个外接圆
②三角形的外心到三角形三个顶点的距离相等,等于 .
③三角形外心的位置:锐角三角形的外心在三角形的 ;直角三角形的外心是 ;钝角三角形的外心在三角形的 .
反证法:
①定义:____________________________________________________________
___________________________
及时练(判断题)
1.过三点一定可以作圆
2.三角形有且只有一个外接圆
3.任意一个圆有一个内接三角形,并且只有一个内接三角形
4.三角形的外心就是这个三角形任意两条垂直平分线的交点
5.三角形的外心到三边的距离相等
三、巩固练习
1.在公园O的附近有E,F,G,H四棵树,位置如图所示(图中小正方形的边长均为1),现计划修建一座以O为圆心,OA为半径的圆形水池,要求池中不留树木,则E,F,G,H四棵树中需要被移除的为( )
A.E,F,G B.F,G,H C.G,H,E D.H,E,F
2.如图,在的正方形网格中,一条圆弧经过A,B,C三点,那么这条圆弧所在圆的圆心为图中的( )
A.点M B.点P C.点Q D.点R
3.如图,在中,,,,CD是斜边AB上的中线,以AC为直径作,设线段CD的中点为P,则点P与的位置关系是( )
A.点P在内 B.点P在上 C.点P在外 D.无法确定
4.如图,在平面直角坐标系中,三个顶点的坐标分别是点,点,点,则的外心的坐标是( )
A. B. C. D.
5.利用反证法证明:“直角三角形至少有一个锐角不小于”时,应先假设( )
A.直角三角形的每个锐角都小于
B.直角三角形有一个锐角大于
C.直角三角形的每个锐角都大于
D.直角三角形有一个锐角小于
6.如图,在中,,,,以点C为圆心,以r为半径作圆,请回答下列问题.
(1)当r取何值时,点A在上,且点B在内部?
(2)当r在什么范围内取值时,点A在外部,且点B在内部?
(3)是否存在这样的实数r,使得点B在上,且点A在内部?
7.如图,圆O是的外接圆,AO平分.
(1)求证:是等腰三角形;
(2)若,,求边BC的长.
8.用反证法证明“等腰三角形的底角都是锐角”.
答案
基础知识
点和圆的位置关系:
①点和圆的三种位置关系:点在圆上,点在圆外,点在圆内.
②OA
③点P在圆内;点P在圆上;点P在圆外,由数量关系得出位置关系.
探究(确定圆的条件):
①经过一个点A作圆,只要以点A以外任意一点为圆心,以这一点与点A的距离为半径就可以作出,这样的圆有无数个,如下图(1).
②经过两点A,B作圆,由于所作圆的圆心到A,B两点的距离相等,所以圆心在线段AB的垂直平分线,这样的圆也可以作出无数个,如下图(2).
③如图,三点A,B,C不在同一条直线上,因为所求的圆要经过A,B,C三点,所以圆心到这三点的距离相等,因此这个点要在线段AB的垂直平分线上,又要在线段BC的垂直平分线上.
(1)分别连接AB,BC,AC;
(2)分别作线段AB,BC的垂直平分线l1和l2,设它们的交点为O,则OA=OB=OC;
(3)以点O为圆心,OA(或OB,OC)为半径作圆,便可以作经过A,B,C三点的圆.
因为过ABC三点的圆的圆心只能是点O,半径等于OA,所以这样的圆只能有一个,即:不在同一条直线上的三点确定一个圆.
三角形的外接圆:
①无数;只有一
②其外接圆的半径
③内部;斜边的中点;外部
反证法:
①假设命题的结论不成立,由此经过推理得出矛盾,由矛盾断定所作假设不正确,从而得到原命题成立.
及时练(判断题)
答案:1.× 2.√ 3.× 4.√ 5.×
巩固练习
1.答案:A
解析:结合网格图可知,,,,,所以E,F,G,H四棵树中需要被移除的为E,F,G,故选A.
2.答案:C
解析:分别作线段AB和BC的垂直平分线,发现它们都经过点Q,所以点Q为这条圆弧所在圆的圆心.故选C.
3.答案:A
解析:在中,,,,O是AC的中点,P是CD的中点,所以OP是的中位线,且.又因为半径,,所以点P在内.
4.答案:D
解析:设点P是的外心.点P到的三个顶点的距离相等,点P是线段BC,AB的垂直平分线的交点.由图可知,点P的坐标为.故选D.
5.答案:A
解析:用反证法证明命题“在直角三角形中,至少有一个锐角不小于”时,应先假设直角三角形的每个锐角都小于.
故选:A.
6.答案:(1)当时,点A在上,且点B在内部
(2)当时,点A在外部,且点B在内部
(3)不存在这样的实数r,使得点B在上,且点A在内部
解析:(1)在中,,,,
.
当时,点A在上,且点B在内部.
(2)当时,点A在外部,且点B在内部.
(3)不存在这样的实数r,使得点B在上,且点A在内部.
7.答案:(1)见解析
(2)
解析:(1)如图,连接OB,OC.
,AO平分,
.
在和中,
,,
是等腰三角形.
(2)如图,延长AO交BC于点H.
平分,,,.
设,.,,,,
解得
.
8.答案:已知:在中,.
求证:都是锐角.
证明:假设都是直角或钝角,
,
,
,
这与三角形内角和为180°矛盾.
假设不成立,原命题的结论正确,
即都是锐角.
2
同课章节目录
