16.2.2 二次根式的除法 课件(共46张PPT)
文档属性
| 名称 | 16.2.2 二次根式的除法 课件(共46张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-17 14:39:50 | ||
图片预览










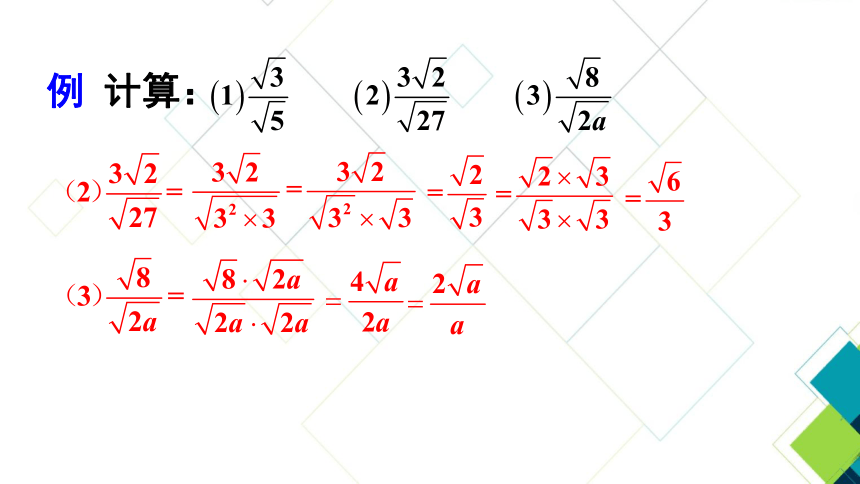
文档简介
(共46张PPT)
第2课时 二次根式的除法
16.2 二次根式的乘除
R·八年级数学下册
新课导入
设长方形的面积为S,相邻两边长分别为a,b,如果 ,那么怎样求a呢?你能列出算式吗?
学习目标
(1)能归纳除法法则公式 (a≥0,b>0),知道 (a≥0,b>0)与 (a≥0,b>0)的意义.
(2)会运用公式 (a≥0,b>0)和 (a≥0, b>0)进行二次根式的除法运算和化简.
探索新知
知识点 1
二次根式除法的运算法则
2
3
=
=
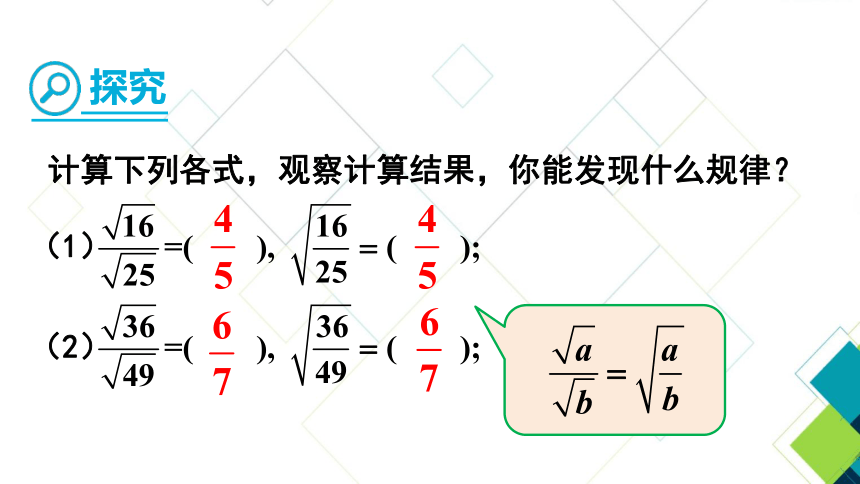
从中你发现了什么规律?
=
=
探究
二次根式的除法法则:
二次根式相除,把被开方数相除,根指数不变.
例 计算:
(1) (2)
解:
把 反过来,就得到
知识点 2
二次根式除法法则的逆运用
利用它可以进行二次根式的化简.
例 化简:
解:
例 计算:
解:
还有其他解法吗?
把分母中的根号化去,使分母变成有理数,这个过程叫做分母有理化.
例 计算:
练习
按照例题化简下列式子.
这些最终化简的式子有什么特点呢?
二次根式的运算结果有以下特点:
(1)被开方数不含分母;
(2)被开方数中不含能开得尽方的因数或因式.
我们把满足上述两个条件的二次根式,叫做最简二次根式.
知识点 3
最简二次根式
即被开方数必须是整数(式)
下列二次根式是否是最简二次根式?为什么?
×
×
×
√
被开方数非整数
被开方数非整数
含可开方的因式
化简下列二次根式,并用最简二次根式的特点验证化简是否彻底.
例 设长方形的面积为S,相邻两边长分别为a,b.已知S=2 ,b= ,求a.
在二次根式的运算中,一般要把最后结果化为最简二次根式,并且分母中不含二次根式.
随堂演练
基础巩固
1.如果等式 成立,那么( )
A.x≥0 B.x>3 C.x≠3 D.x≥3
B
2.下列各式中,是最简二次根式的是( )
C
解:
S△ABC=
6.如图,在Rt△ABC中,∠C=90°,AC= ,S△ABC= ,求AB的长.
A
B
C
综合应用
7.阅读理解与运用.
(1)当x≥0, y≥0时,
同理可得:
(2)a,b均为非负数,且a≠b,化简
误 区 诊 断
误区 一
运算顺序出错
错解:
正解:
错因分析:
进行二次根式的乘除混合运算时,要严格按照运算顺序进行,尤其要注意同级运算应按从左到右的顺序依次计算.
误区 二
通分时忽略分母不能为0的情况
错解:
正解:
错因分析:本题的分子、分母同乘以 时,不允许 a=b,错在没有注意 a=b的情形.当题目中出现字母,且没有告诉字母的取值范围时,特别要注意:字母的取值不能使分母为 0.
课堂小结
今天你学到了哪些知识?
二次根式的除法运算法则是?
二次根式化简后的结果有什么特征?
(1) 被开方数必须是整数(式),
(2) 被开方数不含可开方的因数或因式,
(3) 分母不含二次根式.
拓展延伸
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
习题16.2
第2课时 二次根式的除法
16.2 二次根式的乘除
R·八年级数学下册
新课导入
设长方形的面积为S,相邻两边长分别为a,b,如果 ,那么怎样求a呢?你能列出算式吗?
学习目标
(1)能归纳除法法则公式 (a≥0,b>0),知道 (a≥0,b>0)与 (a≥0,b>0)的意义.
(2)会运用公式 (a≥0,b>0)和 (a≥0, b>0)进行二次根式的除法运算和化简.
探索新知
知识点 1
二次根式除法的运算法则
2
3
=
=
从中你发现了什么规律?
=
=
探究
二次根式的除法法则:
二次根式相除,把被开方数相除,根指数不变.
例 计算:
(1) (2)
解:
把 反过来,就得到
知识点 2
二次根式除法法则的逆运用
利用它可以进行二次根式的化简.
例 化简:
解:
例 计算:
解:
还有其他解法吗?
把分母中的根号化去,使分母变成有理数,这个过程叫做分母有理化.
例 计算:
练习
按照例题化简下列式子.
这些最终化简的式子有什么特点呢?
二次根式的运算结果有以下特点:
(1)被开方数不含分母;
(2)被开方数中不含能开得尽方的因数或因式.
我们把满足上述两个条件的二次根式,叫做最简二次根式.
知识点 3
最简二次根式
即被开方数必须是整数(式)
下列二次根式是否是最简二次根式?为什么?
×
×
×
√
被开方数非整数
被开方数非整数
含可开方的因式
化简下列二次根式,并用最简二次根式的特点验证化简是否彻底.
例 设长方形的面积为S,相邻两边长分别为a,b.已知S=2 ,b= ,求a.
在二次根式的运算中,一般要把最后结果化为最简二次根式,并且分母中不含二次根式.
随堂演练
基础巩固
1.如果等式 成立,那么( )
A.x≥0 B.x>3 C.x≠3 D.x≥3
B
2.下列各式中,是最简二次根式的是( )
C
解:
S△ABC=
6.如图,在Rt△ABC中,∠C=90°,AC= ,S△ABC= ,求AB的长.
A
B
C
综合应用
7.阅读理解与运用.
(1)当x≥0, y≥0时,
同理可得:
(2)a,b均为非负数,且a≠b,化简
误 区 诊 断
误区 一
运算顺序出错
错解:
正解:
错因分析:
进行二次根式的乘除混合运算时,要严格按照运算顺序进行,尤其要注意同级运算应按从左到右的顺序依次计算.
误区 二
通分时忽略分母不能为0的情况
错解:
正解:
错因分析:本题的分子、分母同乘以 时,不允许 a=b,错在没有注意 a=b的情形.当题目中出现字母,且没有告诉字母的取值范围时,特别要注意:字母的取值不能使分母为 0.
课堂小结
今天你学到了哪些知识?
二次根式的除法运算法则是?
二次根式化简后的结果有什么特征?
(1) 被开方数必须是整数(式),
(2) 被开方数不含可开方的因数或因式,
(3) 分母不含二次根式.
拓展延伸
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
习题16.2
