6.1圆周运动 学案 (有答案)
文档属性
| 名称 | 6.1圆周运动 学案 (有答案) |  | |
| 格式 | zip | ||
| 文件大小 | 14.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-11-30 09:33:03 | ||
图片预览




文档简介
6.1圆周运动
一学科核心素养
物理观念:理解描述圆周运动快慢的物理量,体会学科知识间的联系,建立普遍联系的观点。理解各物理量的含义及相互关系,会使用公式计算。
科学思维:根据实例,归纳匀速圆周运动的特点,知道它是一种特殊的变速曲线运动。
科学探究:运用极限法理解线速度。
科学态度与责任:通过观察生活实例、交流与讨论等学习活动,培养学生尊重客观事实、实事求是的科学态度以及学生体验物理与生活的紧密联系。
二学习重难点
重点:线速度、角速度、周期的概念及引入的过程,掌握它们之间的联系。难点:理解线速度、角速度的物理意义及概念引入的必要性。
三课前预习
1.线速度
(1)圆周运动:运动轨迹为_____或一段_____的机械运动。
(2)线速度
①定义:物体运动的_____与时间_____之比。
②定义式:v=_____。
③方向:物体做圆周运动时该点的_____方向。
④物理意义:表示物体在该点运动的_____。
(3)匀速圆周运动:线速度_____处处相等的圆周运动。因线速度的方向在时刻变化,故匀速圆周运动是一种_____运动。
2.实验数据的记录与分析
(1)设计数据记录表格,并将实验数据记录到表格中(表一、表二、表三)
①m、r一定(表一)
序号 1 2 3 4 5 6
Fn
ω
ω2
②m、ω一定(表二)
序号 1 2 3 4 5 6
Fn
r
③r、ω一定(表三)
序号 1 2 3 4 5 6
Fn
m
(2)数据处理
分别作出Fn-ω、Fn-r、Fn-m的图像,若Fn-ω图像不是直线,可以作Fn-ω2图像。
(3)实验结论:
①在质量和半径一定的情况下,向心力的大小与______成正比.
②在质量和角速度一定的情况下,向心力的大小与______成正比.
③在半径和角速度一定的情况下,向心力的大小与______成正比.
3.直径0.6m的飞轮匀速转动,每分钟600转。
(1)转动的周期是_____s
(2)角速度是_____rad/s;
(3)边缘上的线速度是_____m/s。
4.如图为“行星传动示意图”,中心“太阳轮”的转动轴固定,其半径为R1,周围四个“行星轮”的转动轴固定,其半径均为R2,“齿圈”的半径为R3,其中R1=1.5R2,A、B、C分别是“太阳轮”、“行星轮”和“齿圈”边缘上的点,齿轮传动过程不打滑,则A点与C点的线速度之比为________,B点与C点的转速之比为________。
5.位于上海锦江乐园的“摩天轮”,它的高度是120m、直径100m,坐厢内的游客1h可转2.4圈。由此可知,游客转动的周期为_______s,线速度v=_______m/s。
6.如图为某种混凝土搅拌机的传动机构,A轮的齿数为N1,B轮的齿数为N2。当A轮顺时针转动,将带动B轮沿______方向转动,A轮和B轮的角速度之比为________。
7.家用台式计算机上的硬磁盘的磁道和扇区如图所示。某台计算机上的硬磁盘共有N1个磁道(即N1个不同半径的同心圆),每个磁道分成N2个扇区(每扇区为圆周),每个扇区可以记录b个字节。电动机使磁盘每秒转动n圈。磁头在读、写数据时是不动的,磁盘每转一圈,磁头沿半径方向跳动一个磁道。一个扇区通过磁头所用的时间是____________,不计磁头转移磁道的时间,计算机每秒最多可以从一个硬盘面上读取___________个字节。
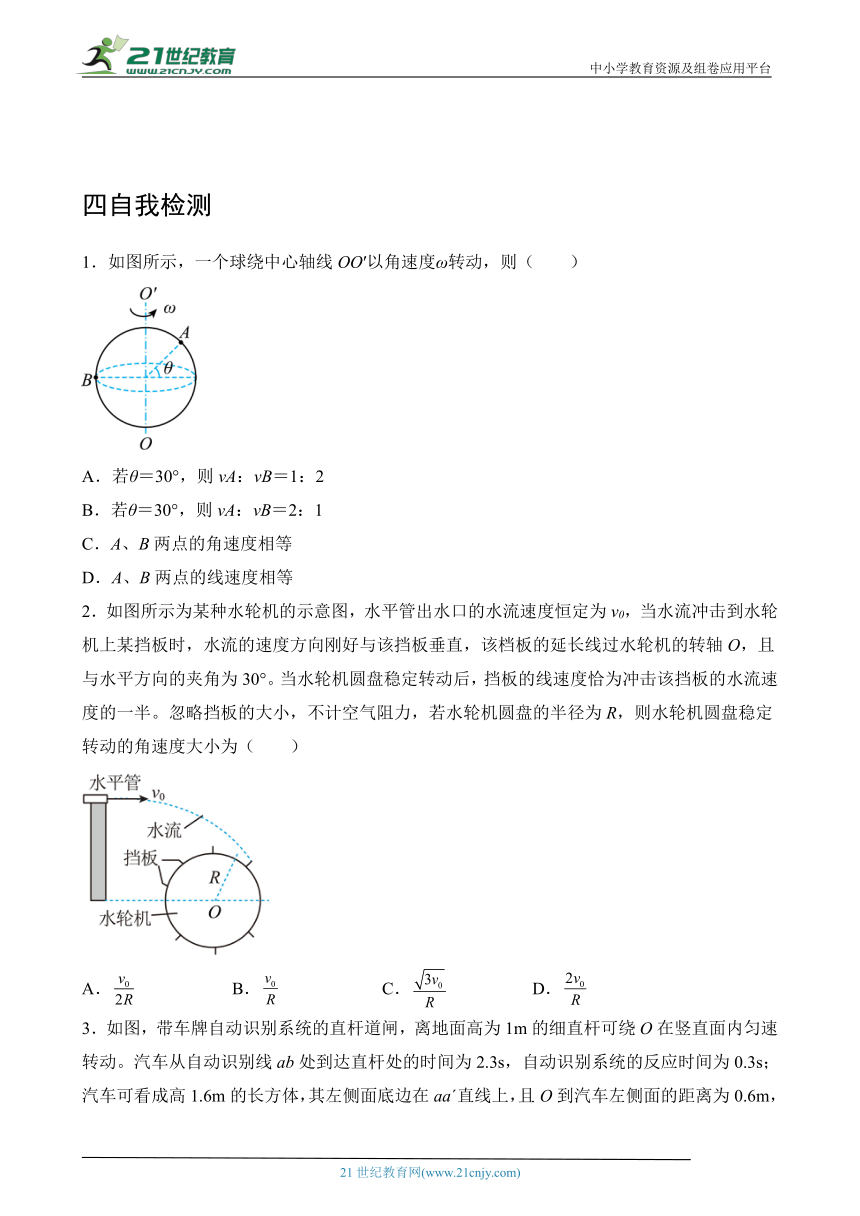
四自我检测
1.如图所示,一个球绕中心轴线OO′以角速度ω转动,则( )
A.若θ=30°,则vA:vB=1:2
B.若θ=30°,则vA:vB=2:1
C.A、B两点的角速度相等
D.A、B两点的线速度相等
2.如图所示为某种水轮机的示意图,水平管出水口的水流速度恒定为v0,当水流冲击到水轮机上某挡板时,水流的速度方向刚好与该挡板垂直,该档板的延长线过水轮机的转轴O,且与水平方向的夹角为30°。当水轮机圆盘稳定转动后,挡板的线速度恰为冲击该挡板的水流速度的一半。忽略挡板的大小,不计空气阻力,若水轮机圆盘的半径为R,则水轮机圆盘稳定转动的角速度大小为( )
A. B. C. D.
3.如图,带车牌自动识别系统的直杆道闸,离地面高为1m的细直杆可绕O在竖直面内匀速转动。汽车从自动识别线ab处到达直杆处的时间为2.3s,自动识别系统的反应时间为0.3s;汽车可看成高1.6m的长方体,其左侧面底边在aaˊ直线上,且O到汽车左侧面的距离为0.6m,要使汽车安全通过道闸,直杆转动的角速度至少为( )
A. B. C. D.
4.修正带是学生常用的学习工具之一,其结构如图所示,包括上下盖座、大小齿轮、压嘴座等部件,大小齿轮分别嵌合于大小轴孔中,大小齿轮相互啮合,a、b两点分别位于大小齿轮的边缘,则关于这两点的线速度大小、角速度关系说法正确的是( )
A.线速度大小相等,角速度不等 B.线速度大小不等,角速度相等
C.线速度大小相等,角速度相等 D.线速度大小不等,角速度不等
5.如图所示为一走时准确的时钟,A、B分别是分针和时针的端点,在时钟正常工作时( )
A. B.
C. D.
6.如图为某一皮带传动装置,主动轮M的半径为,从动轮N的半A径为,已知主动轮做顺时针转动,转速为,转动过程中皮带不打滑。下列说法正确的是( )
A.从动轮做顺时针转动
B.从动轮的角速度大小为
C.从动轮边缘线速度大小为
D.从动轮的转速为
7.如图所示为一链条传动装置的示意图。已知主动轮是逆时针转动的,转速为n,主动轮和从动轮的齿数之比为k,以下说法中正确的是( )
A.从动轮是顺时针转动的
B.主动轮和从动轮边缘的线速度大小相等
C.主动轮和从动轮的角速度大小相等
D.从动轮的转速为
8.某高中开设了糕点制作的选修课,小明同学在体验糕点制作“裱花”环节时,他在绕中心匀速转动的圆盘上放了一块直径20cm的蛋糕,在蛋糕上每隔2s均匀“点”一次奶油,蛋糕一周均匀“点”上15个奶油,则下列说法正确的是( )
A.圆盘转动的转速约为
B.圆盘转动的角速度大小约为
C.蛋糕边缘的奶油线速度大小约为
D.蛋糕边缘的奶油向心加速度约为
9.关于匀速圆周运动,正确的是( )
A.线速度不变 B.角速度不变
C.向心加速度不变 D.匀变速曲线运动
10.如图所示,用起瓶器开启瓶盖时,起瓶器上A、B两点绕O点转动的角速度分别为ωA和ωB,线速度的大小分别为vA和vB,下列说法正确的是( )
A. , B. ,
C. , D. ,
三课前预习
1. 圆周 圆弧 弧长Δs Δt 切线 快慢 大小 变速
2. 角速度的平方 半径 质量
3. 0.1
4. 1:1 7:2
5. 1500##1.5×103
6. 逆时针 N2:N1
7.
四自我检测
参考答案:
1.C
【详解】共轴转动的各点角速度相等,故A、B两点的角速度相等;若θ=30°,A点的转动半径为
B点的转动半径为R,根据公式,线速度之比为
故选C。
2.B
【详解】由几何关系可知,水流冲击挡板时,水流的速度方向与水平方向成60°角,则有
所以水流速度为
根据题意知被冲击后的挡板的线速度为
所以水轮机圆盘稳定转动的角速度大小为
故选B。
3.C
【详解】设汽车恰好通过道闸时直杆转过的角度为,由几何关系得
解得
直杆转动的时间
直杆转动的角速度
故C正确,ABD错误。
故选C。
4.A
【详解】根据题意可知,大小齿轮由于边缘啮合,所以边缘上的点的线速度大小相等,而齿轮的半径不一样,由公式可知,角速度的大小不等。
故选A。
5.B
【详解】A.分针的周期为
时针的周期为
可知
A错误;
B.根据角速度与周期关系
可知角速度与周期成反比,则有
B正确;
CD.根据线速度与角速度关系
由于
,
可知
CD错误;
故选B。
6.B
【详解】A.因为主动轮做顺时针转动,从动轮通过皮带的摩擦力带动转动,所以从动轮逆时针转动,故A错误;
BD.由干通过皮带传动,皮带与轮边缘接触处的线速度相等,根据
得
所以
则
故B正确,D错误;
C.从动轮边缘线速度大小为
故C错误。
故选B。
7.B
【详解】AB.主动轮逆时针转动,带动从动轮也逆时针转动,用链条传动,两轮边缘线速度大小相等,选项A错误,B正确;
C.因为两轮的半径不一样,根据v=rω可知角速度不一样,选项C错误;
D.主动轮和从动轮的齿数之比为k,则有
又
可得
选项D错误。
故选B。
8.C
【详解】A. 在蛋糕上每隔2s均匀“点”一次奶油,蛋糕一周均匀“点”上15个奶油,则圆盘转一圈的周期约为
故圆盘转动的转速约为
A错误;
B. 圆盘转动的角速度大小约为
B错误;
C. 蛋糕边缘的奶油线速度大小约为
C正确;
D. 蛋糕边缘的奶油向心加速度约为
D错误。
故选C。
9.B
【详解】A.匀速圆周运动线速度大小不变,方向沿曲线切线方向,方向时刻改变,A错误;
B.匀速圆周运动角速度大小、方向都不变,B正确;
C.匀速圆周匀速向心加速度大小不变,方向时刻指向圆心,方向时刻改变,C错误;
D.匀速圆周匀速加速度方向时刻改变,不是匀变速曲线匀速,D正确。
故选B。
10.A
【详解】A、B两点绕O点同轴转动,角速度相等,故
由于,根据可知
故选A。
试卷第1页,共3页
试卷第1页,共3页
一学科核心素养
物理观念:理解描述圆周运动快慢的物理量,体会学科知识间的联系,建立普遍联系的观点。理解各物理量的含义及相互关系,会使用公式计算。
科学思维:根据实例,归纳匀速圆周运动的特点,知道它是一种特殊的变速曲线运动。
科学探究:运用极限法理解线速度。
科学态度与责任:通过观察生活实例、交流与讨论等学习活动,培养学生尊重客观事实、实事求是的科学态度以及学生体验物理与生活的紧密联系。
二学习重难点
重点:线速度、角速度、周期的概念及引入的过程,掌握它们之间的联系。难点:理解线速度、角速度的物理意义及概念引入的必要性。
三课前预习
1.线速度
(1)圆周运动:运动轨迹为_____或一段_____的机械运动。
(2)线速度
①定义:物体运动的_____与时间_____之比。
②定义式:v=_____。
③方向:物体做圆周运动时该点的_____方向。
④物理意义:表示物体在该点运动的_____。
(3)匀速圆周运动:线速度_____处处相等的圆周运动。因线速度的方向在时刻变化,故匀速圆周运动是一种_____运动。
2.实验数据的记录与分析
(1)设计数据记录表格,并将实验数据记录到表格中(表一、表二、表三)
①m、r一定(表一)
序号 1 2 3 4 5 6
Fn
ω
ω2
②m、ω一定(表二)
序号 1 2 3 4 5 6
Fn
r
③r、ω一定(表三)
序号 1 2 3 4 5 6
Fn
m
(2)数据处理
分别作出Fn-ω、Fn-r、Fn-m的图像,若Fn-ω图像不是直线,可以作Fn-ω2图像。
(3)实验结论:
①在质量和半径一定的情况下,向心力的大小与______成正比.
②在质量和角速度一定的情况下,向心力的大小与______成正比.
③在半径和角速度一定的情况下,向心力的大小与______成正比.
3.直径0.6m的飞轮匀速转动,每分钟600转。
(1)转动的周期是_____s
(2)角速度是_____rad/s;
(3)边缘上的线速度是_____m/s。
4.如图为“行星传动示意图”,中心“太阳轮”的转动轴固定,其半径为R1,周围四个“行星轮”的转动轴固定,其半径均为R2,“齿圈”的半径为R3,其中R1=1.5R2,A、B、C分别是“太阳轮”、“行星轮”和“齿圈”边缘上的点,齿轮传动过程不打滑,则A点与C点的线速度之比为________,B点与C点的转速之比为________。
5.位于上海锦江乐园的“摩天轮”,它的高度是120m、直径100m,坐厢内的游客1h可转2.4圈。由此可知,游客转动的周期为_______s,线速度v=_______m/s。
6.如图为某种混凝土搅拌机的传动机构,A轮的齿数为N1,B轮的齿数为N2。当A轮顺时针转动,将带动B轮沿______方向转动,A轮和B轮的角速度之比为________。
7.家用台式计算机上的硬磁盘的磁道和扇区如图所示。某台计算机上的硬磁盘共有N1个磁道(即N1个不同半径的同心圆),每个磁道分成N2个扇区(每扇区为圆周),每个扇区可以记录b个字节。电动机使磁盘每秒转动n圈。磁头在读、写数据时是不动的,磁盘每转一圈,磁头沿半径方向跳动一个磁道。一个扇区通过磁头所用的时间是____________,不计磁头转移磁道的时间,计算机每秒最多可以从一个硬盘面上读取___________个字节。
四自我检测
1.如图所示,一个球绕中心轴线OO′以角速度ω转动,则( )
A.若θ=30°,则vA:vB=1:2
B.若θ=30°,则vA:vB=2:1
C.A、B两点的角速度相等
D.A、B两点的线速度相等
2.如图所示为某种水轮机的示意图,水平管出水口的水流速度恒定为v0,当水流冲击到水轮机上某挡板时,水流的速度方向刚好与该挡板垂直,该档板的延长线过水轮机的转轴O,且与水平方向的夹角为30°。当水轮机圆盘稳定转动后,挡板的线速度恰为冲击该挡板的水流速度的一半。忽略挡板的大小,不计空气阻力,若水轮机圆盘的半径为R,则水轮机圆盘稳定转动的角速度大小为( )
A. B. C. D.
3.如图,带车牌自动识别系统的直杆道闸,离地面高为1m的细直杆可绕O在竖直面内匀速转动。汽车从自动识别线ab处到达直杆处的时间为2.3s,自动识别系统的反应时间为0.3s;汽车可看成高1.6m的长方体,其左侧面底边在aaˊ直线上,且O到汽车左侧面的距离为0.6m,要使汽车安全通过道闸,直杆转动的角速度至少为( )
A. B. C. D.
4.修正带是学生常用的学习工具之一,其结构如图所示,包括上下盖座、大小齿轮、压嘴座等部件,大小齿轮分别嵌合于大小轴孔中,大小齿轮相互啮合,a、b两点分别位于大小齿轮的边缘,则关于这两点的线速度大小、角速度关系说法正确的是( )
A.线速度大小相等,角速度不等 B.线速度大小不等,角速度相等
C.线速度大小相等,角速度相等 D.线速度大小不等,角速度不等
5.如图所示为一走时准确的时钟,A、B分别是分针和时针的端点,在时钟正常工作时( )
A. B.
C. D.
6.如图为某一皮带传动装置,主动轮M的半径为,从动轮N的半A径为,已知主动轮做顺时针转动,转速为,转动过程中皮带不打滑。下列说法正确的是( )
A.从动轮做顺时针转动
B.从动轮的角速度大小为
C.从动轮边缘线速度大小为
D.从动轮的转速为
7.如图所示为一链条传动装置的示意图。已知主动轮是逆时针转动的,转速为n,主动轮和从动轮的齿数之比为k,以下说法中正确的是( )
A.从动轮是顺时针转动的
B.主动轮和从动轮边缘的线速度大小相等
C.主动轮和从动轮的角速度大小相等
D.从动轮的转速为
8.某高中开设了糕点制作的选修课,小明同学在体验糕点制作“裱花”环节时,他在绕中心匀速转动的圆盘上放了一块直径20cm的蛋糕,在蛋糕上每隔2s均匀“点”一次奶油,蛋糕一周均匀“点”上15个奶油,则下列说法正确的是( )
A.圆盘转动的转速约为
B.圆盘转动的角速度大小约为
C.蛋糕边缘的奶油线速度大小约为
D.蛋糕边缘的奶油向心加速度约为
9.关于匀速圆周运动,正确的是( )
A.线速度不变 B.角速度不变
C.向心加速度不变 D.匀变速曲线运动
10.如图所示,用起瓶器开启瓶盖时,起瓶器上A、B两点绕O点转动的角速度分别为ωA和ωB,线速度的大小分别为vA和vB,下列说法正确的是( )
A. , B. ,
C. , D. ,
三课前预习
1. 圆周 圆弧 弧长Δs Δt 切线 快慢 大小 变速
2. 角速度的平方 半径 质量
3. 0.1
4. 1:1 7:2
5. 1500##1.5×103
6. 逆时针 N2:N1
7.
四自我检测
参考答案:
1.C
【详解】共轴转动的各点角速度相等,故A、B两点的角速度相等;若θ=30°,A点的转动半径为
B点的转动半径为R,根据公式,线速度之比为
故选C。
2.B
【详解】由几何关系可知,水流冲击挡板时,水流的速度方向与水平方向成60°角,则有
所以水流速度为
根据题意知被冲击后的挡板的线速度为
所以水轮机圆盘稳定转动的角速度大小为
故选B。
3.C
【详解】设汽车恰好通过道闸时直杆转过的角度为,由几何关系得
解得
直杆转动的时间
直杆转动的角速度
故C正确,ABD错误。
故选C。
4.A
【详解】根据题意可知,大小齿轮由于边缘啮合,所以边缘上的点的线速度大小相等,而齿轮的半径不一样,由公式可知,角速度的大小不等。
故选A。
5.B
【详解】A.分针的周期为
时针的周期为
可知
A错误;
B.根据角速度与周期关系
可知角速度与周期成反比,则有
B正确;
CD.根据线速度与角速度关系
由于
,
可知
CD错误;
故选B。
6.B
【详解】A.因为主动轮做顺时针转动,从动轮通过皮带的摩擦力带动转动,所以从动轮逆时针转动,故A错误;
BD.由干通过皮带传动,皮带与轮边缘接触处的线速度相等,根据
得
所以
则
故B正确,D错误;
C.从动轮边缘线速度大小为
故C错误。
故选B。
7.B
【详解】AB.主动轮逆时针转动,带动从动轮也逆时针转动,用链条传动,两轮边缘线速度大小相等,选项A错误,B正确;
C.因为两轮的半径不一样,根据v=rω可知角速度不一样,选项C错误;
D.主动轮和从动轮的齿数之比为k,则有
又
可得
选项D错误。
故选B。
8.C
【详解】A. 在蛋糕上每隔2s均匀“点”一次奶油,蛋糕一周均匀“点”上15个奶油,则圆盘转一圈的周期约为
故圆盘转动的转速约为
A错误;
B. 圆盘转动的角速度大小约为
B错误;
C. 蛋糕边缘的奶油线速度大小约为
C正确;
D. 蛋糕边缘的奶油向心加速度约为
D错误。
故选C。
9.B
【详解】A.匀速圆周运动线速度大小不变,方向沿曲线切线方向,方向时刻改变,A错误;
B.匀速圆周运动角速度大小、方向都不变,B正确;
C.匀速圆周匀速向心加速度大小不变,方向时刻指向圆心,方向时刻改变,C错误;
D.匀速圆周匀速加速度方向时刻改变,不是匀变速曲线匀速,D正确。
故选B。
10.A
【详解】A、B两点绕O点同轴转动,角速度相等,故
由于,根据可知
故选A。
试卷第1页,共3页
试卷第1页,共3页
