6.3 向心加速度 学案 (有答案)
文档属性
| 名称 | 6.3 向心加速度 学案 (有答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-11-30 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
6.3 向心加速度学案
一学科核心素养
【物理观念】树立运动观念,知道向心加速度的表达式,会选择合适的公式用来进行简单的计算;
【科学思维】体会速度变化量的处理特点,体验向心加速度的导出过程,教师启发、引导学生自主阅读、思考、讨论、交流学习成果。
【科学探究】领会推导过程中用到的数学方法。
【科学态度与责任】培养学生思维能力和分析问题的能力,培养学生探究问题的品质。
二学习重难点
【重点】
1、理解匀速圆周运动中加速度的产生原因。
2、掌握向心加速度的确定方法和计算公式。
【难点】
向心加速度方向的确定过程和向心加速度公式的推导与应用。
三课前预习
1.图为一皮带传动装置,大轮C与小轮A固定在同一根轴上,小轮与另一个中等大小的轮子B间用皮带相连,它们的半径之比是。A、B、C分别为轮子边缘上的三个点。
(l)线速度之比_____________。_____________。
(2)角速度之比_____________。_____________。
(3)三点向心加速度之比_____________。
2.如图所示,轮O1、O2固定在同一转轴上,轮O1、O2用皮带连接且不打滑。在O1、O2、O3三个轮的边缘各取一点A、B、C,已知三个轮的半径之比r1∶r2∶r3=2∶1∶1,则:
(1)A、B、C点的线速度大小之比vA∶vB∶vC=___________;
(2)A、B、C点的角速度大小之比ωA∶ωB∶ωC=___________;
(3)A、B、C三点的向心加速度大小之比aA∶aB∶aC=___________。
3.变速圆周运动的受力特点
(1)指向圆心的分力Fn提供______,改变物体速度的______;
(2)沿切向方向的分力Ft改变速度的______,与速度方向相同时物体速度______,与速度方向相反时,物体速度______。
4.匀速圆周运动
(1)定义:做匀速圆周运动的物体所受的指向________的合力。
(2)作用:只改变速度的________。
(3)来源:
①向心力是按力的________来命名的。
②做匀速圆周运动的物体的向心力是由某个力或者几个力的________提供。
5.完成以下填空∶
(1)做变速圆周运动的物体所受合力F不指向圆心,根据F产生的效果,可以把F分解为两个相互垂直的分力∶跟圆周相切的分力Ft和指向圆心的分力Fn。Ft改变物体速度的____;Fn提供物体做圆周运动的向心力,改变物体速度的____。
(2)一般的曲线运动研究方法
对于一般曲线运动,可以把这条曲线分割为许多极短的小段,质点在每一小段的运动都可以看作_______,然后采用圆周运动的分析方法进行处理。
6.匀速圆周运动的加速度方向
(1)定义:物体做匀速圆周运动时的加速度总指向____,这个加速度叫作向心加速度。
(2)向心加速度的作用:向心加速度的方向总是与速度方向___,故向心加速度只改变速度的_____,不改变速度的_____。
(3)物体做匀速圆周运动时,向心加速度始终指向____,方向在时刻____,所以匀速圆周运动是_____曲线运动。
7.如图所示为皮带传动装置,大轮与小轮共轴转动,中轮与小轮通过皮带传动。已知大轮半径为3R,中轮半径为2R,小轮半径为R,C、A、B分别为大、中、小三轮边缘上的一点,假设传动时皮带不打滑,则A、B二点的线速度之比为________,A、B、C三点的向心加速度之比为________。
:
四自我检测
1. 、 两艘快艇在湖面上做匀速圆周运动,在相同时间内,它们通过的路程之比是 ,运动方向改变的角度之比也是 ,则它们( )
A.线速度大小之比为
B.角速度大小之比为
C.圆周运动的半径之比为
D.向心加速度大小之比为
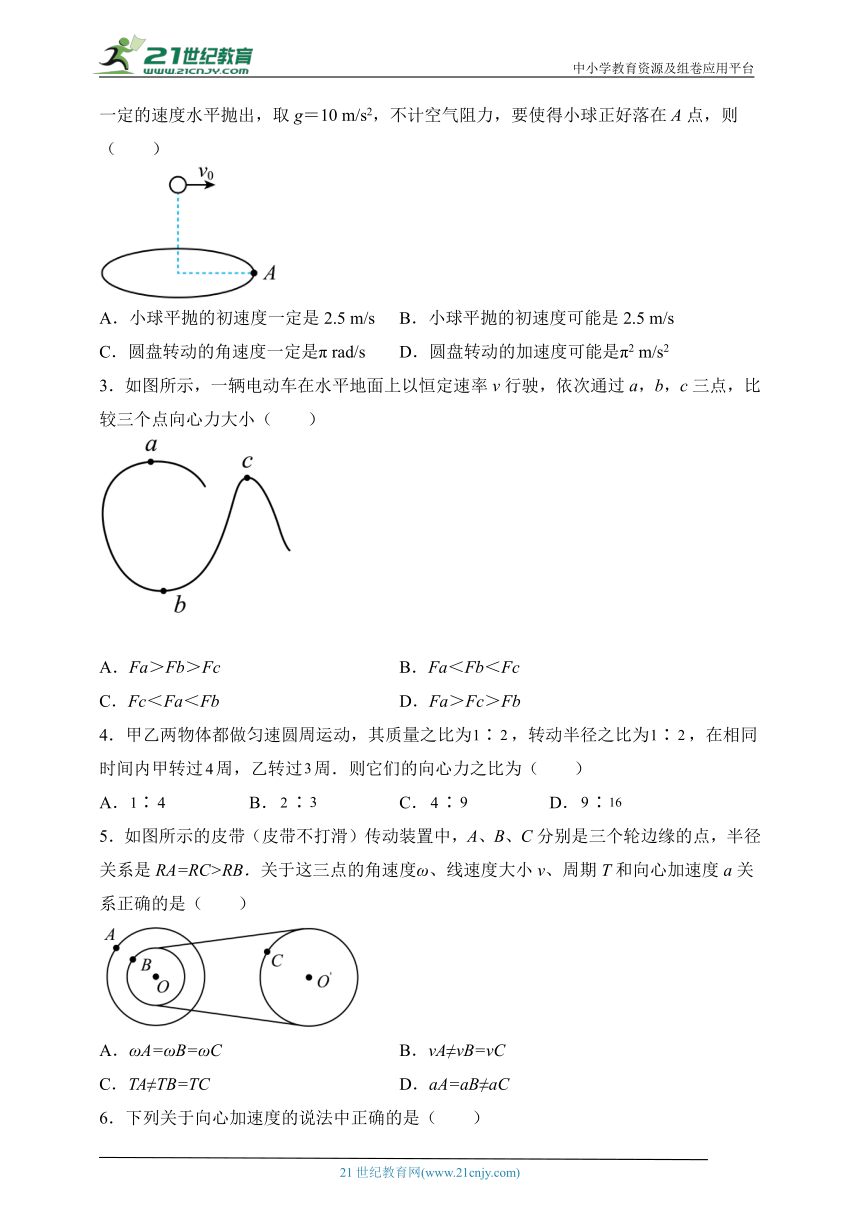
2.如图所示为一个半径为5 m的圆盘,正绕其圆心做匀速转动,当圆盘边缘上的一点A处在如图所示位置的时候,在其圆心正上方20 m的高度有一个小球正在向边缘的A点以一定的速度水平抛出,取g=10 m/s2,不计空气阻力,要使得小球正好落在A点,则( )
A.小球平抛的初速度一定是2.5 m/s B.小球平抛的初速度可能是2.5 m/s
C.圆盘转动的角速度一定是π rad/s D.圆盘转动的加速度可能是π2 m/s2
3.如图所示,一辆电动车在水平地面上以恒定速率v行驶,依次通过a,b,c三点,比较三个点向心力大小( )
A.Fa>Fb>Fc B.Fa<Fb<Fc
C.Fc<Fa<Fb D.Fa>Fc>Fb
4.甲乙两物体都做匀速圆周运动,其质量之比为∶,转动半径之比为∶,在相同时间内甲转过周,乙转过周.则它们的向心力之比为( )
A.∶ B.∶ C.∶ D.∶
5.如图所示的皮带(皮带不打滑)传动装置中,A、B、C分别是三个轮边缘的点,半径关系是RA=RC>RB.关于这三点的角速度ω、线速度大小v、周期T和向心加速度a关系正确的是( )
A.ωA=ωB=ωC B.vA≠vB=vC
C.TA≠TB=TC D.aA=aB≠aC
6.下列关于向心加速度的说法中正确的是( )
A.向心加速度的方向始终指向圆心
B.向心加速度的方向保持不变
C.在匀速圆周运动中,向心加速度是恒定的
D.在变速圆周运动中,向心加速度的方向不指向圆心
7.如图为一种常见的皮带传动装置的示意图,皮带传动时无打滑现象。已知A、B、C三点的半径,,,则A、B、C三点( )
A.线速度之比为
B.角速度之比为
C.向心加速度之比为
D.转动周期之比为
8.如图所示是“陀螺旋转醒酒器”,它可以绕底座的支点旋转,当其转动醒酒时,瓶上的A、B两点,下列说法正确的是( )
A.AB杆上各点角速度大小都相同 B.AB杆上各点线速度大小都相同
C.AB杆上各点加速度大小都相同 D.以上关于AB杆的说法都不正确
9.2018年11月珠海航展,国产全向矢量发动机公开亮相。图为安装了中国国产全向矢量技术发动机的歼-10B战机飞出“眼镜蛇”“落叶飘”等超级机动动作。图为某矢量发动机的模型,O点为发动机转轴,A、B为发动机叶片上的两点,v表示线速度,表示角速度,T表示周期,a表示向心加速度,下列说法正确的是( )
A. B.
C. D.
10.关于质点做匀速圆周运动的下列说法中正确的是( )
A.由知a与r成反比
B.由知a与r成正比
C.由知ω与r成正比
D.由ω=2πn知角速度与转速n成正比
三课前预习
1.
2. 2∶2∶1 1∶2∶1 2∶4∶1
3. 向心力 方向 大小 增大 减小
4. 圆心 方向 作用效果 合力
5. 大小 方向 圆周运动的一部分
6. 圆心 垂直 方向 大小 圆心 变化 变加速
7.
四自我检测
1.D
【详解】A.根据线速度的定义公式
可知,线速度大小之比为,所以A错误;
B.根据角速度的定义公式
可知,角速度大小之比为,所以B错误;
C.根据
则圆周运动的半径之比为,所以C错误;
D.根据
可知,向心加速度大小之比为,所以D正确;
故选D。
2.A
【详解】AB.根据
h=gt2
可得
t==2s
则小球平抛的初速度
v0==2.5m/s
A正确,B错误;
CD.根据
ωt=2nπ(n=1、2、3、…)
解得圆盘转动的角速度
ω==nπ rad/s(n=1、2、3、…)
圆盘转动的加速度为
a=ω2r=n2π2r=5n2π2 m/s2(n=1、2、3、…)
故CD错误。
故选A。
3.B
【详解】根据向心力公式
由于速率恒定,半径越小的位置向心力越大,从图可知曲率半径,故,故B正确,ACD错误。
故选B。
4.C
【详解】在相同时间内甲转过周,乙转过周,所以
∶∶
据匀速圆周运动向心力公式得两个物体向心力之比为
∶∶∶∶
故选C。
5.B
【详解】A、B绕同一转轴转动,角速度ωA=ωB,周期TA=TB,半径不同,线速度大小不同,由a=ω2r可得两点的向心加速度不同,且aA>aB;B、C两点的线速度大小相等,即vB=vC,半径不同,角速度和周期不同,由可知,两点的向心加速度不同,且aB>aC。
故选B。
6.A
【详解】无论是匀速圆周运动还是变速圆周运动,向心加速度的方向都时刻指向圆心,故向心加速度不恒定,故A正确,BCD错误。
故选A。
7.C
【详解】A.皮带传动时无打滑现象,可知A、B两点的线速度相等,B、C两点在同一个轮子上,所以两点B、C的角速度相等,根据
可得
故有
A错误;
B.由于A、B两点的线速度相等,根据
可得
故有
B错误;
C.根据
可得
C正确;
D.根据
可知
故有
D错误。
故选C。
8.A
【详解】A.AB杆上各点,相同时间内转过的角度相同,所以角速度大小相同,故A正确;
B.AB杆上各点做圆周运动的半径不同,角速度相同,根据可知,各点的线速度大小不同,故B错误;
CD.根据可知,各点的加速度大小不同,故CD错误;
故选A。
9.B
【详解】同轴转动,角速度相等,故
而根据线速度和角速度关系可知
因为,所以
圆周运动周期为
因为角速度相同,所以周期也相同。此外向心加速度
因为,所以
故选B。
10.D
【详解】A.由知,在v一定时,a与r成反比,故A错误;
B.由知,在一定时,a与r成正比,故B错误;
C.由知,在v一定时,ω与r成反比,故C错误;
D.由ω=2πn知,角速度与转速n成正比,故D正确。
故选D。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
6.3 向心加速度学案
一学科核心素养
【物理观念】树立运动观念,知道向心加速度的表达式,会选择合适的公式用来进行简单的计算;
【科学思维】体会速度变化量的处理特点,体验向心加速度的导出过程,教师启发、引导学生自主阅读、思考、讨论、交流学习成果。
【科学探究】领会推导过程中用到的数学方法。
【科学态度与责任】培养学生思维能力和分析问题的能力,培养学生探究问题的品质。
二学习重难点
【重点】
1、理解匀速圆周运动中加速度的产生原因。
2、掌握向心加速度的确定方法和计算公式。
【难点】
向心加速度方向的确定过程和向心加速度公式的推导与应用。
三课前预习
1.图为一皮带传动装置,大轮C与小轮A固定在同一根轴上,小轮与另一个中等大小的轮子B间用皮带相连,它们的半径之比是。A、B、C分别为轮子边缘上的三个点。
(l)线速度之比_____________。_____________。
(2)角速度之比_____________。_____________。
(3)三点向心加速度之比_____________。
2.如图所示,轮O1、O2固定在同一转轴上,轮O1、O2用皮带连接且不打滑。在O1、O2、O3三个轮的边缘各取一点A、B、C,已知三个轮的半径之比r1∶r2∶r3=2∶1∶1,则:
(1)A、B、C点的线速度大小之比vA∶vB∶vC=___________;
(2)A、B、C点的角速度大小之比ωA∶ωB∶ωC=___________;
(3)A、B、C三点的向心加速度大小之比aA∶aB∶aC=___________。
3.变速圆周运动的受力特点
(1)指向圆心的分力Fn提供______,改变物体速度的______;
(2)沿切向方向的分力Ft改变速度的______,与速度方向相同时物体速度______,与速度方向相反时,物体速度______。
4.匀速圆周运动
(1)定义:做匀速圆周运动的物体所受的指向________的合力。
(2)作用:只改变速度的________。
(3)来源:
①向心力是按力的________来命名的。
②做匀速圆周运动的物体的向心力是由某个力或者几个力的________提供。
5.完成以下填空∶
(1)做变速圆周运动的物体所受合力F不指向圆心,根据F产生的效果,可以把F分解为两个相互垂直的分力∶跟圆周相切的分力Ft和指向圆心的分力Fn。Ft改变物体速度的____;Fn提供物体做圆周运动的向心力,改变物体速度的____。
(2)一般的曲线运动研究方法
对于一般曲线运动,可以把这条曲线分割为许多极短的小段,质点在每一小段的运动都可以看作_______,然后采用圆周运动的分析方法进行处理。
6.匀速圆周运动的加速度方向
(1)定义:物体做匀速圆周运动时的加速度总指向____,这个加速度叫作向心加速度。
(2)向心加速度的作用:向心加速度的方向总是与速度方向___,故向心加速度只改变速度的_____,不改变速度的_____。
(3)物体做匀速圆周运动时,向心加速度始终指向____,方向在时刻____,所以匀速圆周运动是_____曲线运动。
7.如图所示为皮带传动装置,大轮与小轮共轴转动,中轮与小轮通过皮带传动。已知大轮半径为3R,中轮半径为2R,小轮半径为R,C、A、B分别为大、中、小三轮边缘上的一点,假设传动时皮带不打滑,则A、B二点的线速度之比为________,A、B、C三点的向心加速度之比为________。
:
四自我检测
1. 、 两艘快艇在湖面上做匀速圆周运动,在相同时间内,它们通过的路程之比是 ,运动方向改变的角度之比也是 ,则它们( )
A.线速度大小之比为
B.角速度大小之比为
C.圆周运动的半径之比为
D.向心加速度大小之比为
2.如图所示为一个半径为5 m的圆盘,正绕其圆心做匀速转动,当圆盘边缘上的一点A处在如图所示位置的时候,在其圆心正上方20 m的高度有一个小球正在向边缘的A点以一定的速度水平抛出,取g=10 m/s2,不计空气阻力,要使得小球正好落在A点,则( )
A.小球平抛的初速度一定是2.5 m/s B.小球平抛的初速度可能是2.5 m/s
C.圆盘转动的角速度一定是π rad/s D.圆盘转动的加速度可能是π2 m/s2
3.如图所示,一辆电动车在水平地面上以恒定速率v行驶,依次通过a,b,c三点,比较三个点向心力大小( )
A.Fa>Fb>Fc B.Fa<Fb<Fc
C.Fc<Fa<Fb D.Fa>Fc>Fb
4.甲乙两物体都做匀速圆周运动,其质量之比为∶,转动半径之比为∶,在相同时间内甲转过周,乙转过周.则它们的向心力之比为( )
A.∶ B.∶ C.∶ D.∶
5.如图所示的皮带(皮带不打滑)传动装置中,A、B、C分别是三个轮边缘的点,半径关系是RA=RC>RB.关于这三点的角速度ω、线速度大小v、周期T和向心加速度a关系正确的是( )
A.ωA=ωB=ωC B.vA≠vB=vC
C.TA≠TB=TC D.aA=aB≠aC
6.下列关于向心加速度的说法中正确的是( )
A.向心加速度的方向始终指向圆心
B.向心加速度的方向保持不变
C.在匀速圆周运动中,向心加速度是恒定的
D.在变速圆周运动中,向心加速度的方向不指向圆心
7.如图为一种常见的皮带传动装置的示意图,皮带传动时无打滑现象。已知A、B、C三点的半径,,,则A、B、C三点( )
A.线速度之比为
B.角速度之比为
C.向心加速度之比为
D.转动周期之比为
8.如图所示是“陀螺旋转醒酒器”,它可以绕底座的支点旋转,当其转动醒酒时,瓶上的A、B两点,下列说法正确的是( )
A.AB杆上各点角速度大小都相同 B.AB杆上各点线速度大小都相同
C.AB杆上各点加速度大小都相同 D.以上关于AB杆的说法都不正确
9.2018年11月珠海航展,国产全向矢量发动机公开亮相。图为安装了中国国产全向矢量技术发动机的歼-10B战机飞出“眼镜蛇”“落叶飘”等超级机动动作。图为某矢量发动机的模型,O点为发动机转轴,A、B为发动机叶片上的两点,v表示线速度,表示角速度,T表示周期,a表示向心加速度,下列说法正确的是( )
A. B.
C. D.
10.关于质点做匀速圆周运动的下列说法中正确的是( )
A.由知a与r成反比
B.由知a与r成正比
C.由知ω与r成正比
D.由ω=2πn知角速度与转速n成正比
三课前预习
1.
2. 2∶2∶1 1∶2∶1 2∶4∶1
3. 向心力 方向 大小 增大 减小
4. 圆心 方向 作用效果 合力
5. 大小 方向 圆周运动的一部分
6. 圆心 垂直 方向 大小 圆心 变化 变加速
7.
四自我检测
1.D
【详解】A.根据线速度的定义公式
可知,线速度大小之比为,所以A错误;
B.根据角速度的定义公式
可知,角速度大小之比为,所以B错误;
C.根据
则圆周运动的半径之比为,所以C错误;
D.根据
可知,向心加速度大小之比为,所以D正确;
故选D。
2.A
【详解】AB.根据
h=gt2
可得
t==2s
则小球平抛的初速度
v0==2.5m/s
A正确,B错误;
CD.根据
ωt=2nπ(n=1、2、3、…)
解得圆盘转动的角速度
ω==nπ rad/s(n=1、2、3、…)
圆盘转动的加速度为
a=ω2r=n2π2r=5n2π2 m/s2(n=1、2、3、…)
故CD错误。
故选A。
3.B
【详解】根据向心力公式
由于速率恒定,半径越小的位置向心力越大,从图可知曲率半径,故,故B正确,ACD错误。
故选B。
4.C
【详解】在相同时间内甲转过周,乙转过周,所以
∶∶
据匀速圆周运动向心力公式得两个物体向心力之比为
∶∶∶∶
故选C。
5.B
【详解】A、B绕同一转轴转动,角速度ωA=ωB,周期TA=TB,半径不同,线速度大小不同,由a=ω2r可得两点的向心加速度不同,且aA>aB;B、C两点的线速度大小相等,即vB=vC,半径不同,角速度和周期不同,由可知,两点的向心加速度不同,且aB>aC。
故选B。
6.A
【详解】无论是匀速圆周运动还是变速圆周运动,向心加速度的方向都时刻指向圆心,故向心加速度不恒定,故A正确,BCD错误。
故选A。
7.C
【详解】A.皮带传动时无打滑现象,可知A、B两点的线速度相等,B、C两点在同一个轮子上,所以两点B、C的角速度相等,根据
可得
故有
A错误;
B.由于A、B两点的线速度相等,根据
可得
故有
B错误;
C.根据
可得
C正确;
D.根据
可知
故有
D错误。
故选C。
8.A
【详解】A.AB杆上各点,相同时间内转过的角度相同,所以角速度大小相同,故A正确;
B.AB杆上各点做圆周运动的半径不同,角速度相同,根据可知,各点的线速度大小不同,故B错误;
CD.根据可知,各点的加速度大小不同,故CD错误;
故选A。
9.B
【详解】同轴转动,角速度相等,故
而根据线速度和角速度关系可知
因为,所以
圆周运动周期为
因为角速度相同,所以周期也相同。此外向心加速度
因为,所以
故选B。
10.D
【详解】A.由知,在v一定时,a与r成反比,故A错误;
B.由知,在一定时,a与r成正比,故B错误;
C.由知,在v一定时,ω与r成反比,故C错误;
D.由ω=2πn知,角速度与转速n成正比,故D正确。
故选D。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
