2020-2021学年高中数学人教A版(2019)选择性必修第一册课件:1.1.1空间向量及其线性运算(共22张PPT)
文档属性
| 名称 | 2020-2021学年高中数学人教A版(2019)选择性必修第一册课件:1.1.1空间向量及其线性运算(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-17 20:34:24 | ||
图片预览







文档简介
(共22张PPT)
1.1 空间向量及其运算
第一章 空间向量与立体几何
1.1.1 空间向量及其线性运算
学习目标:
1. 了解空间向量的概念,掌握空间向量的几何表示法和字母表示法;
2. 会用图形说明空间向量加法、减法、数乘向量及它们的运算律;
3. 了解共面向量的意义,掌握其表示方法,理解共线向量定理和共面向量定理及其推论.
教学重点:
空间向量的线性运算和运算律.
教学难点:
共线向量定理及共面向量定理.
探究一 空间向量的概念及表示
空间向量的定义:在空间,我们把具有大小和方向的量叫做空间向量,空间向量的大小叫做空间向量的长度或模 . 空间向量用字母 a,b,c,…表示.
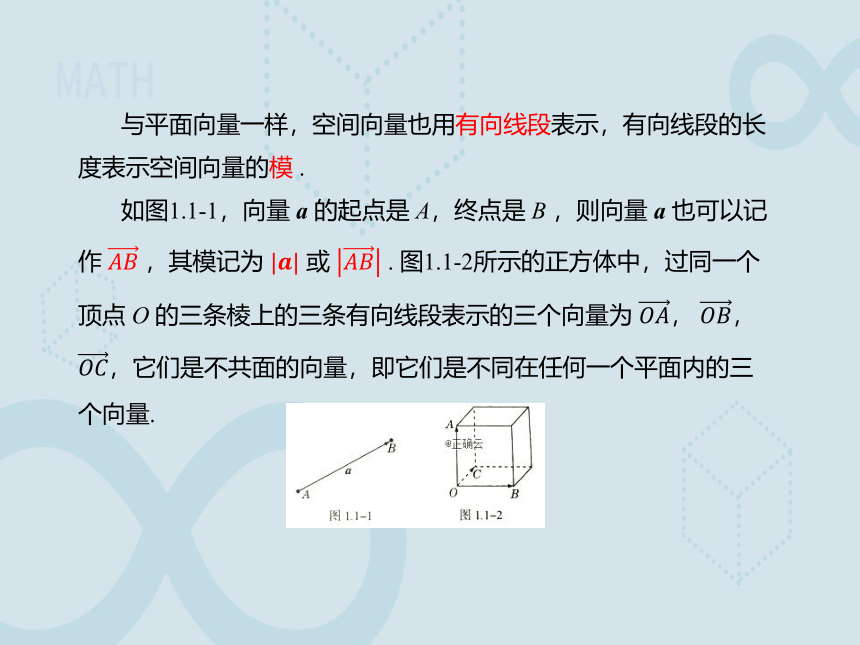
与平面向量一样,空间向量也用有向线段表示,有向线段的长度表示空间向量的模 .
如图1.1-1,向量 a 的起点是 A,终点是 B ,则向量 a 也可以记作 ,其模记为 或 . 图1.1-2所示的正方体中,过同一个顶点 O 的三条棱上的三条有向线段表示的三个向量为 , , ,它们是不共面的向量,即它们是不同在任何一个平面内的三个向量.
长度为 0 的向量叫做零向量,记为 0 .当有向线段的起点 A 与终点 B 重合时, . 模为 1 的向量叫做单位向量 . 与向量 a 长度相等而方向相反的向量,叫做 a 的相反向量,记为 -a.
如果表示若干空间向量的有向线段所在的直线互相平行或重合,那么这些向量叫做共线向量或平行向量.
规定:零向量与任意向量平行,即对于任意向量 a,都有.
方向相同且模相等的向量叫做相等向量 . 因此,在空间,同向且等长的有向线段表示同一向量或相等向量.
空间向量是自由的,对于空间中的任意两个非零向量,可以通过平移使它们的起点重合. 因为两条相交直线确定一个平面,所以起点重合的两个不共线向量可以确定一个平面,也就是说,任意两个空间向量都可以平移到同一个平面内,成为同一平面内的两个向量. 如图1.1-3,已知空间向量 a,b ,以任意点 O 为起点,作向量 ,,我们就可以把它们平移到同一个平面 α 内.
问题1 平面向量与空间向量有什么区别与联系?
(1)区别:平面向量研究的是二维平面的向量,空间向量研究的是三维空间的向量.
(2)联系:空间向量的定义、表示方法及零向量、单位向量、相反向量、相等向量和共线向量(平行向量)的概念都与平面向量相同.
探究二 空间向量的线性运算
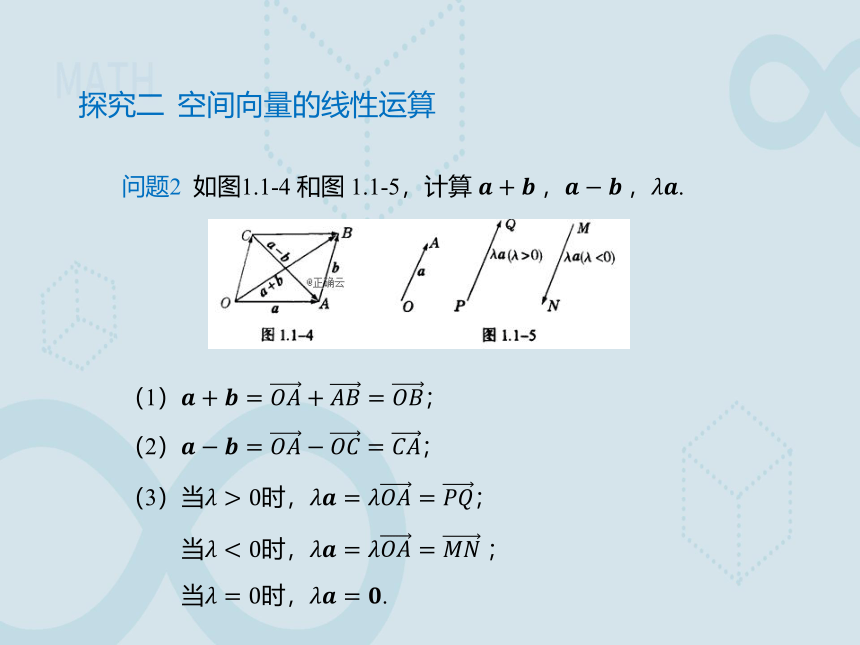
问题2 如图1.1-4 和图 1.1-5,计算 .
(1);
(2);
(3)当时,;
当时, ;
当时,.
问题3 由此是否能得出空间向量线性运算的运算律?
空间向量线性运算的运算律:
(1)交换律:
;
(2)结合律:
;
(3)分配律:
,
.
问题4 如图1.1-6,在平行六面体 中,分别标出 , 表示的向量.从中体会向量加法运算的交换律和结合律.一般地,三个不共面的向量的和与这三个向量有什么关系?
在平行四边形 ABCD 中, ;在平行四边形中, ;在平行四边形中, ;在平行四边形 中, .故 .一般地,对于三个不共面的向量 a,b,c,以任意点 O 为起点,a,b,c 为邻边作平行六面体,则 a,b,c 的和等于以 O 为起点的平行六面体对角线所表示的向量.利用向量加法的交换律和结合律,可以得到:有限个向量求和,交换相加向量的顺序,其和不变.
探究三 共线向量及共面向量
问题5 对任意两个空间向量 a 与 b,如果 ,a与 b有什么位置关系?反过来,a 与 b 有什么位置关系时,?
类似于平面向量共线的充要条件,对任意两个空间向量 a,b
,的充要条件是存在实数 λ ,使 .(共线向量定理)
如图1.1-7,O 是直线 l 上一点,在直线l上取非零向量 a ,则对于直线 l 上任意一点 P ,由数乘向量的定义及向量共线的充要条件可知,存在实数 λ ,使得 .
与向量 a 平行的非零向量称为直线 l 的方向向量.
这样,直线 l 上任意一点都可以由直线l上的一点和它的方向向量表示,也就是说,直线可以由其上一点和它的方向向量确定.
如图1.1-8,如果表示向量 a 的有向线段 所在的直线 OA 与直线 l 平行或重合,那么称向量 a 平行于直线 l . 如果直线 OA 平行于平面 α 或在平面 α 内,那么称向量 a 平行于平面 α .平行于同一个平面的向量,叫做共面向量.
问题6 我们知道,任意两个空间向量总是共面的,但三个空间向量既可能是共面的,也可能是不共面的 . 那么,什么情况下三个空间向量共面呢?
带着问题6来进行探究.
问题7 对平面内任意两个不共线向量 a,b,由平面向量基本定理可知,这个平面内的任意一个向量 p 可以写成 ,其中 (x,y) 是唯一确定的有序实数对 . 对两个不共线的空间向量 a,b,如果,那么向量 p 与向量 a,b 有什么位置关系?反过来,向量 p 与向量 a,b 有什么位置关系时,?
可以发现,如果两个向量 a,b 不共线,那么向量 p 与向量 a,b共面的充要条件是存在唯一的有序实数对 (x,y),使 .(共面向量定理)
例1 如图1.1-9,已知平行四边形 ABCD ,过平面 AC 外一点 O 作射线 OA,OB,OC,OD ,在四条射线上分别取点 E,F,G,H,使 . 求证:E,F,G,H 四点共面.
1.下列命题:
①若向量a,b共线,则向量a,b所在的直线平行;②若向量a,b所在的直线为异面直线,则向量a,b一定不共面;③若三个向量a,b,c两两共面,则向量a,b,c共面;④分别表示空间向量的两条有向线段所在的直线是异面直线,则这两个向量不是共面向量.
其中正确命题的个数是( )
A.0 B.1 C.2 D.3
练一练
A
解析:a与b共线,a,b 所在直线也可能重合,故①错误;根据向量的意义知,空间任意两向量 a,b 都共面,故②错误;三个向量 a,b,c 中任意两个一定共线,但它们三个却不一定共面,故③错误;因为空间任意两向量平移之后均可共面,所以空间任意两向量均共面,故④错误.综上可知四个命题中正确的个数为 0,故选A.
练一练
A
练一练
A
练一练
课堂小结
——你学到了那些新知识呢?
空间向量的概念;
空间向量的线性运算;
空间共线向量与共面向量.
1.1 空间向量及其运算
第一章 空间向量与立体几何
1.1.1 空间向量及其线性运算
学习目标:
1. 了解空间向量的概念,掌握空间向量的几何表示法和字母表示法;
2. 会用图形说明空间向量加法、减法、数乘向量及它们的运算律;
3. 了解共面向量的意义,掌握其表示方法,理解共线向量定理和共面向量定理及其推论.
教学重点:
空间向量的线性运算和运算律.
教学难点:
共线向量定理及共面向量定理.
探究一 空间向量的概念及表示
空间向量的定义:在空间,我们把具有大小和方向的量叫做空间向量,空间向量的大小叫做空间向量的长度或模 . 空间向量用字母 a,b,c,…表示.
与平面向量一样,空间向量也用有向线段表示,有向线段的长度表示空间向量的模 .
如图1.1-1,向量 a 的起点是 A,终点是 B ,则向量 a 也可以记作 ,其模记为 或 . 图1.1-2所示的正方体中,过同一个顶点 O 的三条棱上的三条有向线段表示的三个向量为 , , ,它们是不共面的向量,即它们是不同在任何一个平面内的三个向量.
长度为 0 的向量叫做零向量,记为 0 .当有向线段的起点 A 与终点 B 重合时, . 模为 1 的向量叫做单位向量 . 与向量 a 长度相等而方向相反的向量,叫做 a 的相反向量,记为 -a.
如果表示若干空间向量的有向线段所在的直线互相平行或重合,那么这些向量叫做共线向量或平行向量.
规定:零向量与任意向量平行,即对于任意向量 a,都有.
方向相同且模相等的向量叫做相等向量 . 因此,在空间,同向且等长的有向线段表示同一向量或相等向量.
空间向量是自由的,对于空间中的任意两个非零向量,可以通过平移使它们的起点重合. 因为两条相交直线确定一个平面,所以起点重合的两个不共线向量可以确定一个平面,也就是说,任意两个空间向量都可以平移到同一个平面内,成为同一平面内的两个向量. 如图1.1-3,已知空间向量 a,b ,以任意点 O 为起点,作向量 ,,我们就可以把它们平移到同一个平面 α 内.
问题1 平面向量与空间向量有什么区别与联系?
(1)区别:平面向量研究的是二维平面的向量,空间向量研究的是三维空间的向量.
(2)联系:空间向量的定义、表示方法及零向量、单位向量、相反向量、相等向量和共线向量(平行向量)的概念都与平面向量相同.
探究二 空间向量的线性运算
问题2 如图1.1-4 和图 1.1-5,计算 .
(1);
(2);
(3)当时,;
当时, ;
当时,.
问题3 由此是否能得出空间向量线性运算的运算律?
空间向量线性运算的运算律:
(1)交换律:
;
(2)结合律:
;
(3)分配律:
,
.
问题4 如图1.1-6,在平行六面体 中,分别标出 , 表示的向量.从中体会向量加法运算的交换律和结合律.一般地,三个不共面的向量的和与这三个向量有什么关系?
在平行四边形 ABCD 中, ;在平行四边形中, ;在平行四边形中, ;在平行四边形 中, .故 .一般地,对于三个不共面的向量 a,b,c,以任意点 O 为起点,a,b,c 为邻边作平行六面体,则 a,b,c 的和等于以 O 为起点的平行六面体对角线所表示的向量.利用向量加法的交换律和结合律,可以得到:有限个向量求和,交换相加向量的顺序,其和不变.
探究三 共线向量及共面向量
问题5 对任意两个空间向量 a 与 b,如果 ,a与 b有什么位置关系?反过来,a 与 b 有什么位置关系时,?
类似于平面向量共线的充要条件,对任意两个空间向量 a,b
,的充要条件是存在实数 λ ,使 .(共线向量定理)
如图1.1-7,O 是直线 l 上一点,在直线l上取非零向量 a ,则对于直线 l 上任意一点 P ,由数乘向量的定义及向量共线的充要条件可知,存在实数 λ ,使得 .
与向量 a 平行的非零向量称为直线 l 的方向向量.
这样,直线 l 上任意一点都可以由直线l上的一点和它的方向向量表示,也就是说,直线可以由其上一点和它的方向向量确定.
如图1.1-8,如果表示向量 a 的有向线段 所在的直线 OA 与直线 l 平行或重合,那么称向量 a 平行于直线 l . 如果直线 OA 平行于平面 α 或在平面 α 内,那么称向量 a 平行于平面 α .平行于同一个平面的向量,叫做共面向量.
问题6 我们知道,任意两个空间向量总是共面的,但三个空间向量既可能是共面的,也可能是不共面的 . 那么,什么情况下三个空间向量共面呢?
带着问题6来进行探究.
问题7 对平面内任意两个不共线向量 a,b,由平面向量基本定理可知,这个平面内的任意一个向量 p 可以写成 ,其中 (x,y) 是唯一确定的有序实数对 . 对两个不共线的空间向量 a,b,如果,那么向量 p 与向量 a,b 有什么位置关系?反过来,向量 p 与向量 a,b 有什么位置关系时,?
可以发现,如果两个向量 a,b 不共线,那么向量 p 与向量 a,b共面的充要条件是存在唯一的有序实数对 (x,y),使 .(共面向量定理)
例1 如图1.1-9,已知平行四边形 ABCD ,过平面 AC 外一点 O 作射线 OA,OB,OC,OD ,在四条射线上分别取点 E,F,G,H,使 . 求证:E,F,G,H 四点共面.
1.下列命题:
①若向量a,b共线,则向量a,b所在的直线平行;②若向量a,b所在的直线为异面直线,则向量a,b一定不共面;③若三个向量a,b,c两两共面,则向量a,b,c共面;④分别表示空间向量的两条有向线段所在的直线是异面直线,则这两个向量不是共面向量.
其中正确命题的个数是( )
A.0 B.1 C.2 D.3
练一练
A
解析:a与b共线,a,b 所在直线也可能重合,故①错误;根据向量的意义知,空间任意两向量 a,b 都共面,故②错误;三个向量 a,b,c 中任意两个一定共线,但它们三个却不一定共面,故③错误;因为空间任意两向量平移之后均可共面,所以空间任意两向量均共面,故④错误.综上可知四个命题中正确的个数为 0,故选A.
练一练
A
练一练
A
练一练
课堂小结
——你学到了那些新知识呢?
空间向量的概念;
空间向量的线性运算;
空间共线向量与共面向量.
