13.1.2 第2课时 线段垂直平分线的性质 课件(共18张PPT)
文档属性
| 名称 | 13.1.2 第2课时 线段垂直平分线的性质 课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 976.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-17 17:56:14 | ||
图片预览




文档简介
(共18张PPT)
13.1.2 第2课时
线段垂直平分线的性质
人教版 八年级上册
教学目标
【教学目标】
1.知识与技能
(1)掌握线段垂直平分线的性质和判定。
(2)能运用线段垂直平分线的性质和判定解决实际问题。
2.过程与方法
探究线段垂直平分线的性质,培养学生认真探究、积极思考的能力。
3.情感态度和价值观
在探究的过程中,更大程度的激发学生学习的主动性和积极性,并使学生具有一些初步研究问题的能力。
【重点】线段垂直平分线的性质
【难点】线段垂直平分的性质的运用
情景导入
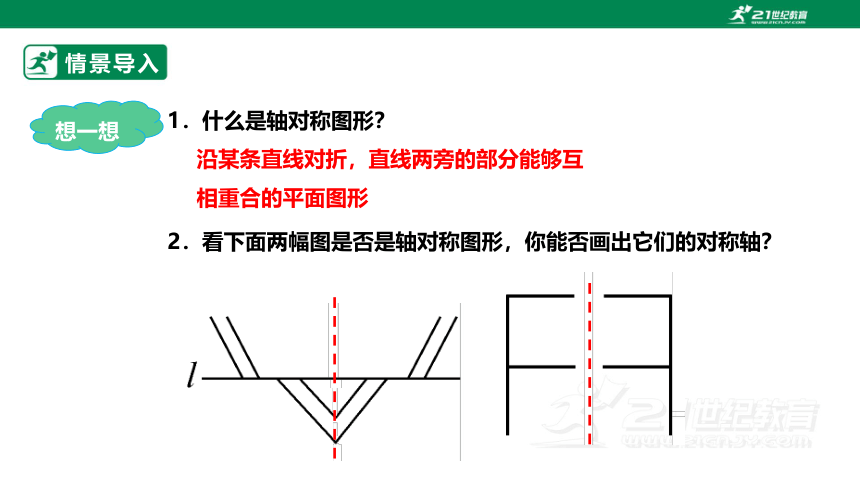
1.什么是轴对称图形?
2.看下面两幅图是否是轴对称图形,你能否画出它们的对称轴?
想一想
沿某条直线对折,直线两旁的部分能够互相重合的平面图形
新知探究
问题1:有时我们感觉一(两)个平面图形是轴对称的,如何验证呢?
A
B
C
A ′
B ′
C ′
通过折叠,如果这(两)个图形能够互相重合,则这(两)个图形是轴对称图形.
问题2:不折叠图形,你能准确地作出轴对称图形的对称轴吗?
例题讲解
例2 如图,点A和点B关于某条直线成轴对称,你能作出这条直线吗?
A
B
分析:我们只要连接点A和点B,作出线段AB的垂直平分线,就可得到点A和点B的对称轴.为此作出到点A,B的距离相等的两点,即线段AB的垂直平分线上的两点,从而作出线段AB的垂直平分线.
新知探究
A
B
C
D
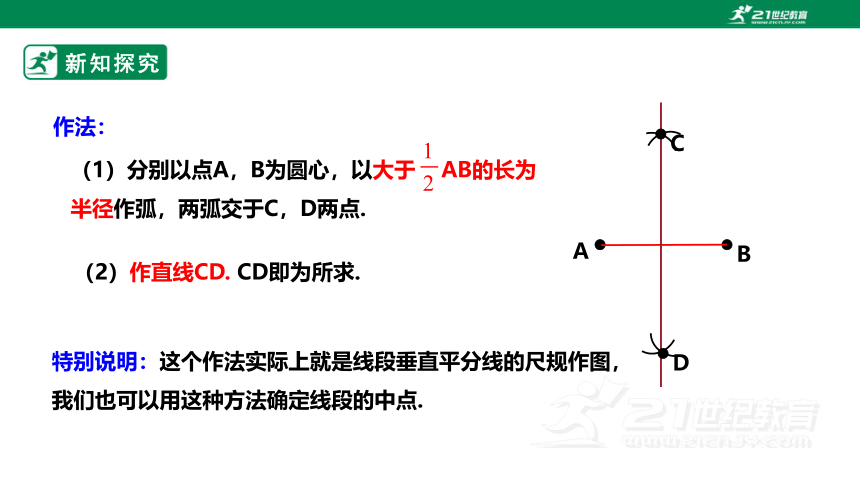
作法:
(1)分别以点A,B为圆心,以大于 AB的长为半径作弧,两弧交于C,D两点.
(2)作直线CD. CD即为所求.
特别说明:这个作法实际上就是线段垂直平分线的尺规作图,我们也可以用这种方法确定线段的中点.
新知探究
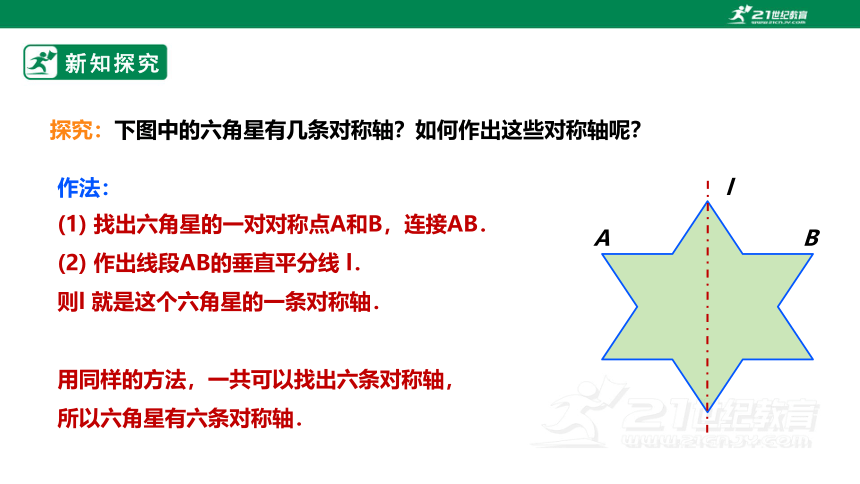
探究:下图中的六角星有几条对称轴?如何作出这些对称轴呢?
A
B
作法:
(1) 找出六角星的一对对称点A和B,连接AB.
(2) 作出线段AB的垂直平分线 l.
则l 就是这个六角星的一条对称轴.
l
用同样的方法,一共可以找出六条对称轴,
所以六角星有六条对称轴.
总结归纳
对称轴的作法:
如果两个图形成轴对称,其对称轴就是任何一对对应点所连线段的垂直平分线.因此,我们只要找到一对对应点,作出连接它们的线段的垂直平分线, 就可以得到这两个图形的对称轴.
新知探究
如图,A,B是路边两个新建小区,要在公路边增设一个公共汽车站.使两个小区到车站的路程一样长,该公共汽车站应建在什么地方?
A
B
公共汽车站
总结归纳
方法总结:
①过成轴对称图形的两组对应点的连线(或延长线)交点的直线是这个轴对称图形的对称轴.
②如果成轴对称的两个图形对称点连线(或延长线)相交,那么交点必定在对称轴上.
课堂练习
1.如图所示的尺规作图是作( )
A.线段的垂直平分线
B.一条线段等于已知线段
C.角的平分线
D.一个角等于已知角
A
课堂练习
2.如图,已知△ABC,求作一点P,使P点到∠CAB的两边的距离相等,且PA=PB.下列确定P点的方法正确的是( )
A.P为∠CAB,∠ABC两角平分线的交点
B.P为∠CAB的平分线与AB的垂直平分线的交点
C.P为AC,AB两边上的高 的交点
D.P为AC ,AB两边的垂直平分线的交点
B
课堂练习
3.如图,在△ABC中,AB>AC.按以下步骤作图:分别以点B和点C为圆心,大于BC一半的长为半径作圆弧,两弧相交于点M和点N;作直线MN交AB于点D;连接CD.若AB=6,AC=4,则△ACD的周长为______.
10
课堂练习
4.如图,有A,B,C三个村庄,现准备要建一所希望小学,要求学校到三个村庄的距离相等,请你确定学校的位置.
B
C
学校在连接任意两点的两条线段的垂直平分线的交点处.
A
课堂练习
5.如图,在△ABC中,∠C=60°,∠A=4 0°.
(1)用尺规作图作AB的垂直平分线,交AC于点D,交AB于点E(保留作图痕迹,不要求写作法和证明);
(2)求证:BD平分∠CBA.
解:(1)如图1所示:
(2)连接BD,如图2所示:
∵∠C=60°,∠A=40°,∴∠CBA=80°,
∵DE是AB的垂直平分线,∴∠A=∠DBA=40°,
∴∠DBA=∠CBA,
∴BD平分∠CBA.
课堂小结
作线段的
垂直平分线
基本作图
作对称轴
(1) 将图形对折;
(2) 用尺规作图;
(3) 用刻度尺先取一对对称点连线的中点,然后作垂线
(1) 作一条线段等于已知线段;
(2) 作一个角等于已知角;
(3) 作一个角的平分线;
(4) 经过已知直线外一点作这条直线的垂线;
(5) 作已知线段的垂直平分线.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
13.1.2 第2课时
线段垂直平分线的性质
人教版 八年级上册
教学目标
【教学目标】
1.知识与技能
(1)掌握线段垂直平分线的性质和判定。
(2)能运用线段垂直平分线的性质和判定解决实际问题。
2.过程与方法
探究线段垂直平分线的性质,培养学生认真探究、积极思考的能力。
3.情感态度和价值观
在探究的过程中,更大程度的激发学生学习的主动性和积极性,并使学生具有一些初步研究问题的能力。
【重点】线段垂直平分线的性质
【难点】线段垂直平分的性质的运用
情景导入
1.什么是轴对称图形?
2.看下面两幅图是否是轴对称图形,你能否画出它们的对称轴?
想一想
沿某条直线对折,直线两旁的部分能够互相重合的平面图形
新知探究
问题1:有时我们感觉一(两)个平面图形是轴对称的,如何验证呢?
A
B
C
A ′
B ′
C ′
通过折叠,如果这(两)个图形能够互相重合,则这(两)个图形是轴对称图形.
问题2:不折叠图形,你能准确地作出轴对称图形的对称轴吗?
例题讲解
例2 如图,点A和点B关于某条直线成轴对称,你能作出这条直线吗?
A
B
分析:我们只要连接点A和点B,作出线段AB的垂直平分线,就可得到点A和点B的对称轴.为此作出到点A,B的距离相等的两点,即线段AB的垂直平分线上的两点,从而作出线段AB的垂直平分线.
新知探究
A
B
C
D
作法:
(1)分别以点A,B为圆心,以大于 AB的长为半径作弧,两弧交于C,D两点.
(2)作直线CD. CD即为所求.
特别说明:这个作法实际上就是线段垂直平分线的尺规作图,我们也可以用这种方法确定线段的中点.
新知探究
探究:下图中的六角星有几条对称轴?如何作出这些对称轴呢?
A
B
作法:
(1) 找出六角星的一对对称点A和B,连接AB.
(2) 作出线段AB的垂直平分线 l.
则l 就是这个六角星的一条对称轴.
l
用同样的方法,一共可以找出六条对称轴,
所以六角星有六条对称轴.
总结归纳
对称轴的作法:
如果两个图形成轴对称,其对称轴就是任何一对对应点所连线段的垂直平分线.因此,我们只要找到一对对应点,作出连接它们的线段的垂直平分线, 就可以得到这两个图形的对称轴.
新知探究
如图,A,B是路边两个新建小区,要在公路边增设一个公共汽车站.使两个小区到车站的路程一样长,该公共汽车站应建在什么地方?
A
B
公共汽车站
总结归纳
方法总结:
①过成轴对称图形的两组对应点的连线(或延长线)交点的直线是这个轴对称图形的对称轴.
②如果成轴对称的两个图形对称点连线(或延长线)相交,那么交点必定在对称轴上.
课堂练习
1.如图所示的尺规作图是作( )
A.线段的垂直平分线
B.一条线段等于已知线段
C.角的平分线
D.一个角等于已知角
A
课堂练习
2.如图,已知△ABC,求作一点P,使P点到∠CAB的两边的距离相等,且PA=PB.下列确定P点的方法正确的是( )
A.P为∠CAB,∠ABC两角平分线的交点
B.P为∠CAB的平分线与AB的垂直平分线的交点
C.P为AC,AB两边上的高 的交点
D.P为AC ,AB两边的垂直平分线的交点
B
课堂练习
3.如图,在△ABC中,AB>AC.按以下步骤作图:分别以点B和点C为圆心,大于BC一半的长为半径作圆弧,两弧相交于点M和点N;作直线MN交AB于点D;连接CD.若AB=6,AC=4,则△ACD的周长为______.
10
课堂练习
4.如图,有A,B,C三个村庄,现准备要建一所希望小学,要求学校到三个村庄的距离相等,请你确定学校的位置.
B
C
学校在连接任意两点的两条线段的垂直平分线的交点处.
A
课堂练习
5.如图,在△ABC中,∠C=60°,∠A=4 0°.
(1)用尺规作图作AB的垂直平分线,交AC于点D,交AB于点E(保留作图痕迹,不要求写作法和证明);
(2)求证:BD平分∠CBA.
解:(1)如图1所示:
(2)连接BD,如图2所示:
∵∠C=60°,∠A=40°,∴∠CBA=80°,
∵DE是AB的垂直平分线,∴∠A=∠DBA=40°,
∴∠DBA=∠CBA,
∴BD平分∠CBA.
课堂小结
作线段的
垂直平分线
基本作图
作对称轴
(1) 将图形对折;
(2) 用尺规作图;
(3) 用刻度尺先取一对对称点连线的中点,然后作垂线
(1) 作一条线段等于已知线段;
(2) 作一个角等于已知角;
(3) 作一个角的平分线;
(4) 经过已知直线外一点作这条直线的垂线;
(5) 作已知线段的垂直平分线.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
