正弦定理和余弦定理的应用举例
图片预览










文档简介
课件45张PPT。第八节 正弦定理、余弦定理的应用举例1.仰角和俯角
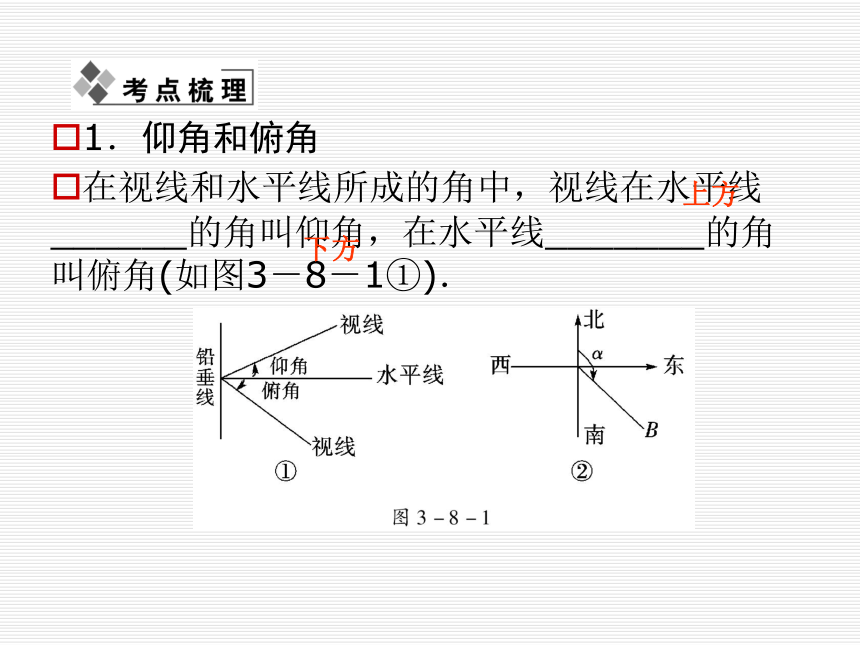
在视线和水平线所成的角中,视线在水平线______的角叫仰角,在水平线_______的角叫俯角(如图3-8-1①).上方下方2.方位角和方向角
(1)方位角:从指北方向_________转到目标方向线的水平角,如B点的方位角为α(如图3-8-1②).
(2)方向角:相对于某正方向的水平角,如南偏东30°等.
3.坡度与坡比
坡度:坡面与水平面所成的二面角的度数.
坡比:坡面的铅直高度与水平长度之比.顺时针1.仰角、俯角、方位角有什么区别?
【提示】 三者的参照不同.仰角与俯角是相对于水平线而言的,而方位角是相对于正北方向而言的.
2.如何用方位角、方向角确定一点的位置?
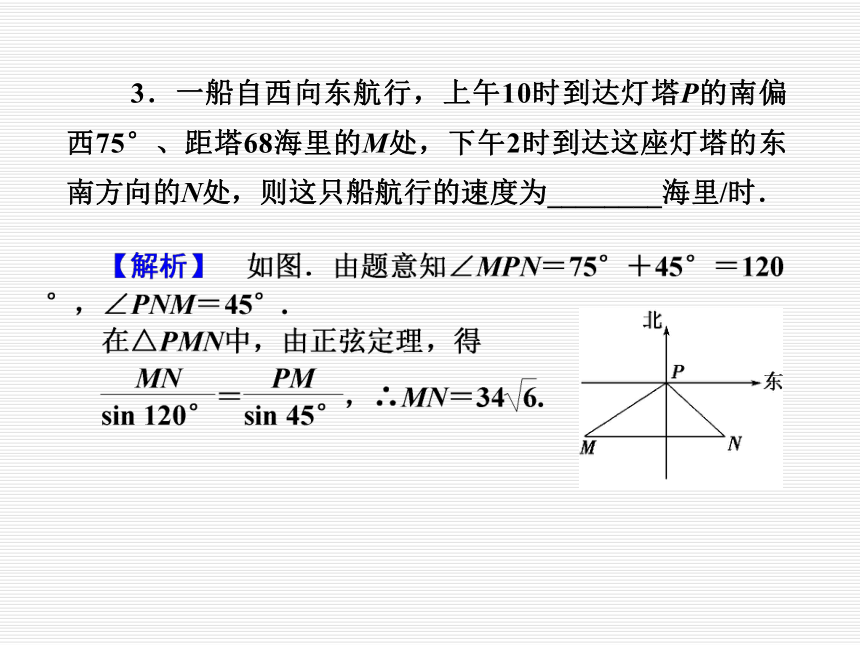
【提示】 利用方位角或方向角和目标与观测点的距离即可唯一确定一点的位置.【答案】 B2.在相距2千米的A、B两点处测量目标点C,若∠CAB=75°,∠CBA=60°,则A、C两点之间的距离为________千米. 3.一船自西向东航行,上午10时到达灯塔P的南偏西75°、距塔68海里的M处,下午2时到达这座灯塔的东南方向的N处,则这只船航行的速度为________海里/时.4.(2013·梅州模拟)如图3-8-3,为了测量河的宽度,在一岸边选定两点A,B望对岸的标记物C,测得∠CAB=30°,∠CBA=75°,AB=120 m.则这条河的宽度为________m.【答案】 60
1.利用示意图把已知量和待求量尽量集中在有关三角形中,建立一个解三角形的模型;
2.利用正、余弦定理解出所求的边和角,得出该数学模型的解.【思路点拨】 用|AC|表示|BC|,在△ABC中,根据余弦定理列方程求|AC|,在△ACH中,求|CH|.
1.在测量高度时,要准确理解仰角、俯角的概念,仰角和俯角都是在同一铅垂面内,视线与水平线的夹角;
2.分清已知条件与所求,画出示意图;明确在哪个三角形内运用正、余弦定理,有序地解相关的三角形. 某人在C点测得某塔在南偏西80°,塔顶A仰角为45°,此人沿南偏东40°方向前进10米到D,测得塔顶A的仰角为30°,求该塔的高度.
测量角度问题的一般步骤
(1)在弄清题意的基础上,画出表示实际问题的图形,并在图形中标出有关的角和距离;
(2)用正弦定理或余弦定理解三角形;
(3)将解得的结果转化为实际问题的解.如图3-8-7所示,位于A处
的信息中心获悉:在其正东
方向相距40海里的B处有一
艘渔船遇险,在原地等待营
救.信息中心立即把消息告
知在其南偏西30°、相距20海里的C处的乙船,现乙船朝北偏东θ的方向沿直线CB前往B处救援,求cos θ的值.图3-8-7解三角形应用题的一般步骤:
(1)阅读理解题意,弄清问题的实际背景,明确已知与未知,理清量与量之间的关系.
(2)根据题意画出示意图,将实际问题抽象成解三角形问题的模型.
(3)根据题意选择正弦定理或余弦定理求解.
(4)将三角形问题还原为实际问题,注意实际问题中的有关单位问题、近似计算的要求等.解三角形应用题常有以下两种情形:
(1)实际问题经抽象概括后,已知量与未知量全部集中在一个三角形中,可用正弦定理或余弦定理求解.
(2)实际问题经抽象概括后,已知量与未知量涉及到两个或两个以上的三角形,这时需作出这些三角形,先解够条件的三角形,然后逐步求解其他三角形,有时需设出未知量,从几个三角形中列出方程(组),解方程(组)得出所要求的解.
从近两年高考试题看,高考对正、余弦定理的实际应用考察较少,但此部分内容能较好地考察学生的阅读理解能力,分析问题和解决问题的能力及函数与方程的思想,因此应积极备考.思想方法之八 构建三角形模型解决实际应用问题
(2013·清远模拟)某港口O要将一件重要物品用小艇送到一艘正在航行的轮船上.在小艇出发时,轮船位于港口O北偏西30°且与该港口相距20海里的A处,并正以30海里/小时的航行速度沿正东方向匀速行驶,假设该小艇沿直线方向以v海里/小时的航行速度匀速行驶,经过t小时与轮船相遇.
(1)若希望相遇时小艇的航行距离最小,则小艇航行速度的大小应为多少?(2)假设小艇的最高航行速度只能达到30海里/小时,试设计航行方案(即确定航行方向和航行速度的大小),使得小艇能以最短时间与轮船相遇,并说明理由.
易错提示:(1)理解能力差,方向角概念不清,不能根据题设条件做出示意图,导致无法入手;
(2)主要是不会构建v与t的函数关系式,难以利用条件解不等式.
防范措施:(1)理清方向角的概念,准确画出相关示意图.
(2)在△AOB中,根据题设条件,恰当选择正弦(余弦)定理求解.【答案】 15 m2.(2013·惠州模拟)某航模
兴趣小组的同学,为了测定在
湖面上航模航行的速度,采用
如下办法:在岸边设置两个观
察点A,B,且AB长为80米,
当航模在C处时,测得∠ABC=105°和∠BAC=30°,经过20秒后,航模直线航行到D处,测得∠BAD=90°和∠ABD=45°.请你根据以上条件求出航模的速度.(答案保留根号)课后作业(二十五)
在视线和水平线所成的角中,视线在水平线______的角叫仰角,在水平线_______的角叫俯角(如图3-8-1①).上方下方2.方位角和方向角
(1)方位角:从指北方向_________转到目标方向线的水平角,如B点的方位角为α(如图3-8-1②).
(2)方向角:相对于某正方向的水平角,如南偏东30°等.
3.坡度与坡比
坡度:坡面与水平面所成的二面角的度数.
坡比:坡面的铅直高度与水平长度之比.顺时针1.仰角、俯角、方位角有什么区别?
【提示】 三者的参照不同.仰角与俯角是相对于水平线而言的,而方位角是相对于正北方向而言的.
2.如何用方位角、方向角确定一点的位置?
【提示】 利用方位角或方向角和目标与观测点的距离即可唯一确定一点的位置.【答案】 B2.在相距2千米的A、B两点处测量目标点C,若∠CAB=75°,∠CBA=60°,则A、C两点之间的距离为________千米. 3.一船自西向东航行,上午10时到达灯塔P的南偏西75°、距塔68海里的M处,下午2时到达这座灯塔的东南方向的N处,则这只船航行的速度为________海里/时.4.(2013·梅州模拟)如图3-8-3,为了测量河的宽度,在一岸边选定两点A,B望对岸的标记物C,测得∠CAB=30°,∠CBA=75°,AB=120 m.则这条河的宽度为________m.【答案】 60
1.利用示意图把已知量和待求量尽量集中在有关三角形中,建立一个解三角形的模型;
2.利用正、余弦定理解出所求的边和角,得出该数学模型的解.【思路点拨】 用|AC|表示|BC|,在△ABC中,根据余弦定理列方程求|AC|,在△ACH中,求|CH|.
1.在测量高度时,要准确理解仰角、俯角的概念,仰角和俯角都是在同一铅垂面内,视线与水平线的夹角;
2.分清已知条件与所求,画出示意图;明确在哪个三角形内运用正、余弦定理,有序地解相关的三角形. 某人在C点测得某塔在南偏西80°,塔顶A仰角为45°,此人沿南偏东40°方向前进10米到D,测得塔顶A的仰角为30°,求该塔的高度.
测量角度问题的一般步骤
(1)在弄清题意的基础上,画出表示实际问题的图形,并在图形中标出有关的角和距离;
(2)用正弦定理或余弦定理解三角形;
(3)将解得的结果转化为实际问题的解.如图3-8-7所示,位于A处
的信息中心获悉:在其正东
方向相距40海里的B处有一
艘渔船遇险,在原地等待营
救.信息中心立即把消息告
知在其南偏西30°、相距20海里的C处的乙船,现乙船朝北偏东θ的方向沿直线CB前往B处救援,求cos θ的值.图3-8-7解三角形应用题的一般步骤:
(1)阅读理解题意,弄清问题的实际背景,明确已知与未知,理清量与量之间的关系.
(2)根据题意画出示意图,将实际问题抽象成解三角形问题的模型.
(3)根据题意选择正弦定理或余弦定理求解.
(4)将三角形问题还原为实际问题,注意实际问题中的有关单位问题、近似计算的要求等.解三角形应用题常有以下两种情形:
(1)实际问题经抽象概括后,已知量与未知量全部集中在一个三角形中,可用正弦定理或余弦定理求解.
(2)实际问题经抽象概括后,已知量与未知量涉及到两个或两个以上的三角形,这时需作出这些三角形,先解够条件的三角形,然后逐步求解其他三角形,有时需设出未知量,从几个三角形中列出方程(组),解方程(组)得出所要求的解.
从近两年高考试题看,高考对正、余弦定理的实际应用考察较少,但此部分内容能较好地考察学生的阅读理解能力,分析问题和解决问题的能力及函数与方程的思想,因此应积极备考.思想方法之八 构建三角形模型解决实际应用问题
(2013·清远模拟)某港口O要将一件重要物品用小艇送到一艘正在航行的轮船上.在小艇出发时,轮船位于港口O北偏西30°且与该港口相距20海里的A处,并正以30海里/小时的航行速度沿正东方向匀速行驶,假设该小艇沿直线方向以v海里/小时的航行速度匀速行驶,经过t小时与轮船相遇.
(1)若希望相遇时小艇的航行距离最小,则小艇航行速度的大小应为多少?(2)假设小艇的最高航行速度只能达到30海里/小时,试设计航行方案(即确定航行方向和航行速度的大小),使得小艇能以最短时间与轮船相遇,并说明理由.
易错提示:(1)理解能力差,方向角概念不清,不能根据题设条件做出示意图,导致无法入手;
(2)主要是不会构建v与t的函数关系式,难以利用条件解不等式.
防范措施:(1)理清方向角的概念,准确画出相关示意图.
(2)在△AOB中,根据题设条件,恰当选择正弦(余弦)定理求解.【答案】 15 m2.(2013·惠州模拟)某航模
兴趣小组的同学,为了测定在
湖面上航模航行的速度,采用
如下办法:在岸边设置两个观
察点A,B,且AB长为80米,
当航模在C处时,测得∠ABC=105°和∠BAC=30°,经过20秒后,航模直线航行到D处,测得∠BAD=90°和∠ABD=45°.请你根据以上条件求出航模的速度.(答案保留根号)课后作业(二十五)
