粤教版 必修一 2.1 知识与智慧 课件(共22张)
文档属性
| 名称 | 粤教版 必修一 2.1 知识与智慧 课件(共22张) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 粤教版(2019) | ||
| 科目 | 信息科技(信息技术) | ||
| 更新时间 | 2022-10-19 14:42:37 | ||
图片预览





文档简介
(共23张PPT)
知识与数字化学习
粤教版(2019版) 信息技术(高中)
2.1知识与智慧
必修1 数据与计算
第二章
1、知识
2、智慧
学习目标
重点:知识
难点:智慧
重难点
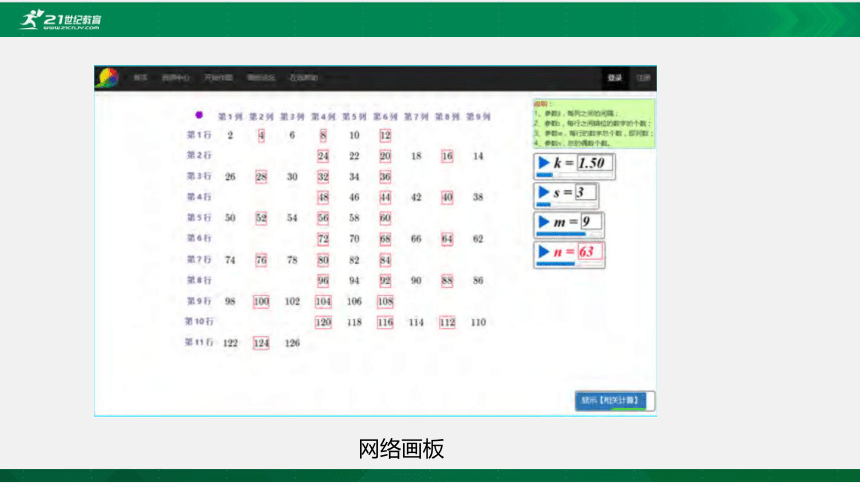
未来教室里,教师们运用Python、思维导图、网络画板(图2-1)等各类数字化学习 工具进行个性化教学,使教学更加形象、直观、易懂;同学们利用数字化学习工具进行个 性化学习,不仅可以开阔视野、开发思维、启迪智慧,而且可以直观地感受知识形成的过 程,提高学习效率。
网络画板
思维导图
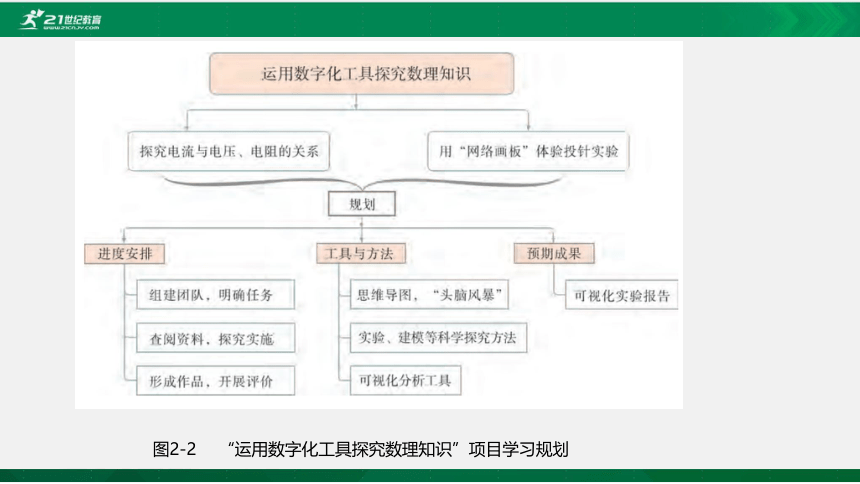
图2-2 “运用数字化工具探究数理知识”项目学习规划
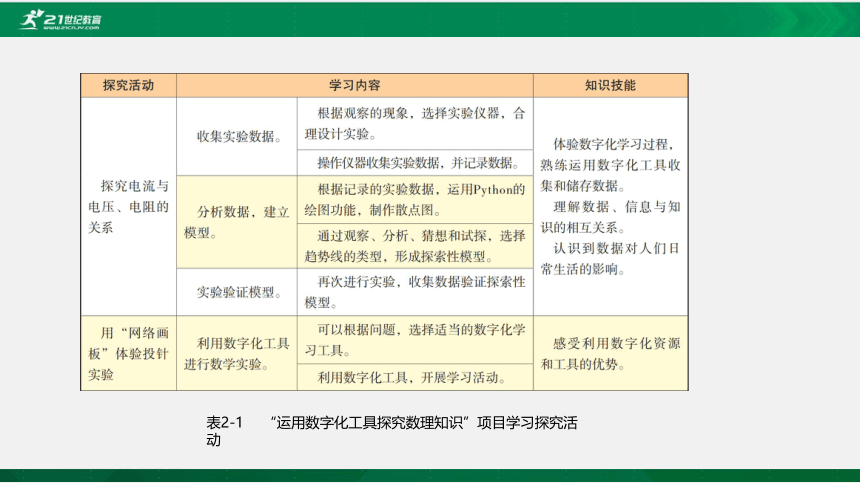
表2-1 “运用数字化工具探究数理知识”项目学习探究活动
在人类的生产、生活和研究活动中,人们会不断学习、总结、发现认识自然、探究 规律的方法。“做实验→获取观察数据→分析处理数据→推理建立数学模型→实验验证 模型→形成知识→应用知识解决问题”是一条非常有效的知识发现路径。
课堂导入
2.1.1知识
知识是人们运用大脑对获取或积累的信息进行系统化地提炼、研究和分析的结果,能 够精确地反映事物的本质。它来源于实践,经过加工提炼,又高于实践。
欧姆在研究电流与电压、电阻关系的实验中利用了控制变量法,即保持电压不变,探 究电流和电阻的关系;或保持电阻不变,探究电流和电压的关系。 下面我们运用Python工具,利用控制变量法采集实验数据,研究当导体电压保持不变 时,通过导体的电流随导体电阻变化的规律。
图2-4 欧姆定律实验简化示意图
实验仪器 电压表、电流表、电池、开关、导线、滑动变阻器和10个不同阻值的电阻。
实验步骤
(1)收集实验数据。
①连接电路图如图2-4所示。连接电路时注意:接 线时开关要断开;闭合开关前,滑动变阻器的滑片要滑 到最大阻值处。
②把电阻R1(记下阻值)接入电路,移动滑动变阻 器的滑片,使电压表示数U=3 V,记录电流表示数I1。
③把电阻R1换成电阻R2(记下阻值),再次移动滑 动变阻器的滑片,使电压表示数U=3 V,记录电流表示 数I2。
④如此类推,把电阻R9换成电阻R10,再次移动滑片,使电压表示数U=3 V,记录电流 表示数I10。
表2-2 欧姆定律实验的观察数据
(2)运用Python工具处理数据,绘制图像。
①绘制散点图。可以从教科书配套学习资源包中安装Python解释器Jupyter notebook, 运行配套学习资源包“第二章\课本素材\绘制散点图”程序,把表2-2中的数据输入程序 中,执行程序后得到如图2-5所示的电流I与电阻R关系数据散点图。
②在“绘制散点图”程序中加上指令“plt.plot(x0,y0)”,执行程序后,得到如图 2-6所示的电流I与电阻R关系数据曲线图。
图2-5 电流I 与电阻R 关系数据散点图
图2-6 电流I 与电阻R 关系数据曲线图
图2-7 电流I 与电阻R 关系数据曲线拟合图
③观察电流 I 与电阻 R 关系数据曲线 图后,可以猜想电流 I 与电阻 R 的关系是 反比例关系,于是按 I =U/R 的关系对数据 做曲线拟合。打开配套学习资源包“第 二章\课本素材\曲线拟合”程序,执行 程序后得到如图2-7所示的电流I与电 阻 R 关系数据曲线拟合图。其中, U=2905.67607341 mV与电压表的示数基 本吻合,即I=
④经过推理和实验验证,电流 I 与电 阻R反比例关系成立,即I=U/R 。
2 . 1 . 2 智慧
图2-8 数据、信息、知识和智慧的相互关系
数据、信息、知识和智慧是逐渐递进的概念,前者是后者的基础和前提,后者是前者 的抽象与升华。从数据到信息的转化,主要理解数据间的相互联系;从信息到知识的转 化,主要理解信息间的相互联系,发现和抽象其规律;从知识到智慧的转化,主要理解和 应用知识原理与法则解决现实世界的问题。
科学研究的第三种方法——计算方法
科学研究主要依靠理论方法和实验方法。理论方法是指以数学学科为代表,以推 理和演绎为特征的方法。研究人员通过构建分析模型和理论推导进行规律预测与发 现。实验方法是指以物理学科为代表,以实验、观察和总结为特征的方法。研究人员 通过直接观察获取数据,对数据进行分析,进而发现规律,获得知识。 随着移动互联网和物联网的飞速发展,现实世界的各种事物都变得可感知、可度量, 从而生成数量庞大的数据或数据群,基于庞大数据形成的仿真系统成为可能。因此,依靠 计算发现和预测规律成为与理论方法和实验方法并存的科学研究的第三种方法。研究人员 通过建立仿真的分析模型和有效的算法,利用计算工具来进行规律发现和预测。 依靠计算方法发现和预测规律已成为不同学科的科学家进行研究的重要方法。
例如, 生物学家利用计算方法研究生命体的特性,化学家利用计算方法研究化学反应的机理,建筑学家利用计算方法来研究建筑结构的抗震性,社会学家利用计算方法研究社会群体网络 的各种特性等。 由此,计算方法与各学科结合形成了所谓的计算科学,如计算物理学、计算化学、计 算生物学、计算经济学等。 我们所使用的工具影响 着我们的思维方式和思维习惯,从而也深刻影响着我们的思维能力。” 研究人员在利用计算方法进行创新研究的同时,也在不断地研究新型的计算方法。 这种结合不同专业的新型计算方法的研究需要专业知识与计算思维的结合。1998年,John Pople便因成功地研究出量子化学综合软件包Gaussian而获得诺贝尔奖,Gaussian已成为研究 化学领域许多课题的重要的计算方法。另一个典型的计算方法是求解应力或疲劳等结构力 学、多物理场耦合的有限元分析方法。利用先进的计算方法的虚拟现实、增强现实等技术 也在各个领域创造出令人惊喜的视觉效果。
THANKS
“
”
知识与数字化学习
粤教版(2019版) 信息技术(高中)
2.1知识与智慧
必修1 数据与计算
第二章
1、知识
2、智慧
学习目标
重点:知识
难点:智慧
重难点
未来教室里,教师们运用Python、思维导图、网络画板(图2-1)等各类数字化学习 工具进行个性化教学,使教学更加形象、直观、易懂;同学们利用数字化学习工具进行个 性化学习,不仅可以开阔视野、开发思维、启迪智慧,而且可以直观地感受知识形成的过 程,提高学习效率。
网络画板
思维导图
图2-2 “运用数字化工具探究数理知识”项目学习规划
表2-1 “运用数字化工具探究数理知识”项目学习探究活动
在人类的生产、生活和研究活动中,人们会不断学习、总结、发现认识自然、探究 规律的方法。“做实验→获取观察数据→分析处理数据→推理建立数学模型→实验验证 模型→形成知识→应用知识解决问题”是一条非常有效的知识发现路径。
课堂导入
2.1.1知识
知识是人们运用大脑对获取或积累的信息进行系统化地提炼、研究和分析的结果,能 够精确地反映事物的本质。它来源于实践,经过加工提炼,又高于实践。
欧姆在研究电流与电压、电阻关系的实验中利用了控制变量法,即保持电压不变,探 究电流和电阻的关系;或保持电阻不变,探究电流和电压的关系。 下面我们运用Python工具,利用控制变量法采集实验数据,研究当导体电压保持不变 时,通过导体的电流随导体电阻变化的规律。
图2-4 欧姆定律实验简化示意图
实验仪器 电压表、电流表、电池、开关、导线、滑动变阻器和10个不同阻值的电阻。
实验步骤
(1)收集实验数据。
①连接电路图如图2-4所示。连接电路时注意:接 线时开关要断开;闭合开关前,滑动变阻器的滑片要滑 到最大阻值处。
②把电阻R1(记下阻值)接入电路,移动滑动变阻 器的滑片,使电压表示数U=3 V,记录电流表示数I1。
③把电阻R1换成电阻R2(记下阻值),再次移动滑 动变阻器的滑片,使电压表示数U=3 V,记录电流表示 数I2。
④如此类推,把电阻R9换成电阻R10,再次移动滑片,使电压表示数U=3 V,记录电流 表示数I10。
表2-2 欧姆定律实验的观察数据
(2)运用Python工具处理数据,绘制图像。
①绘制散点图。可以从教科书配套学习资源包中安装Python解释器Jupyter notebook, 运行配套学习资源包“第二章\课本素材\绘制散点图”程序,把表2-2中的数据输入程序 中,执行程序后得到如图2-5所示的电流I与电阻R关系数据散点图。
②在“绘制散点图”程序中加上指令“plt.plot(x0,y0)”,执行程序后,得到如图 2-6所示的电流I与电阻R关系数据曲线图。
图2-5 电流I 与电阻R 关系数据散点图
图2-6 电流I 与电阻R 关系数据曲线图
图2-7 电流I 与电阻R 关系数据曲线拟合图
③观察电流 I 与电阻 R 关系数据曲线 图后,可以猜想电流 I 与电阻 R 的关系是 反比例关系,于是按 I =U/R 的关系对数据 做曲线拟合。打开配套学习资源包“第 二章\课本素材\曲线拟合”程序,执行 程序后得到如图2-7所示的电流I与电 阻 R 关系数据曲线拟合图。其中, U=2905.67607341 mV与电压表的示数基 本吻合,即I=
④经过推理和实验验证,电流 I 与电 阻R反比例关系成立,即I=U/R 。
2 . 1 . 2 智慧
图2-8 数据、信息、知识和智慧的相互关系
数据、信息、知识和智慧是逐渐递进的概念,前者是后者的基础和前提,后者是前者 的抽象与升华。从数据到信息的转化,主要理解数据间的相互联系;从信息到知识的转 化,主要理解信息间的相互联系,发现和抽象其规律;从知识到智慧的转化,主要理解和 应用知识原理与法则解决现实世界的问题。
科学研究的第三种方法——计算方法
科学研究主要依靠理论方法和实验方法。理论方法是指以数学学科为代表,以推 理和演绎为特征的方法。研究人员通过构建分析模型和理论推导进行规律预测与发 现。实验方法是指以物理学科为代表,以实验、观察和总结为特征的方法。研究人员 通过直接观察获取数据,对数据进行分析,进而发现规律,获得知识。 随着移动互联网和物联网的飞速发展,现实世界的各种事物都变得可感知、可度量, 从而生成数量庞大的数据或数据群,基于庞大数据形成的仿真系统成为可能。因此,依靠 计算发现和预测规律成为与理论方法和实验方法并存的科学研究的第三种方法。研究人员 通过建立仿真的分析模型和有效的算法,利用计算工具来进行规律发现和预测。 依靠计算方法发现和预测规律已成为不同学科的科学家进行研究的重要方法。
例如, 生物学家利用计算方法研究生命体的特性,化学家利用计算方法研究化学反应的机理,建筑学家利用计算方法来研究建筑结构的抗震性,社会学家利用计算方法研究社会群体网络 的各种特性等。 由此,计算方法与各学科结合形成了所谓的计算科学,如计算物理学、计算化学、计 算生物学、计算经济学等。 我们所使用的工具影响 着我们的思维方式和思维习惯,从而也深刻影响着我们的思维能力。” 研究人员在利用计算方法进行创新研究的同时,也在不断地研究新型的计算方法。 这种结合不同专业的新型计算方法的研究需要专业知识与计算思维的结合。1998年,John Pople便因成功地研究出量子化学综合软件包Gaussian而获得诺贝尔奖,Gaussian已成为研究 化学领域许多课题的重要的计算方法。另一个典型的计算方法是求解应力或疲劳等结构力 学、多物理场耦合的有限元分析方法。利用先进的计算方法的虚拟现实、增强现实等技术 也在各个领域创造出令人惊喜的视觉效果。
THANKS
“
”
同课章节目录
- 第一章 数据与信息
- 项目范例 体验庆祝国庆多媒体作品的数据与信息处理
- 1.1 数据及其特征
- 1.2 数据编码
- 1.3 信息及其特征
- 第二章 知识与数字化学习
- 项目范例 运用数字化工具探究数理知识
- 2.1 知识与智慧
- 2.2 数字化学习与创新
- 第三章 算法基础
- 项目范例 设计从A市到B市耗时最少的旅行路线方案
- 3.1 体验计算机解决问题的过程
- 3.2 算法及其描述
- 3.3 计算机程序与程序设计语言
- 第四章 程序设计基础
- 项目范例 设计购买纪念品的最佳方案
- 4.1 程序设计语言的基础知识
- 4.2 运用顺序结构描述问题求解过程
- 4.3 运用选择结构描述问题求解过程
- 4.4 运用循环结构描述问题求解过程
- 第五章 数据处理和可视化表达
- 项目范例 网络购物平台客户行为数据分析和可视化表达
- 5.1 认识大数据
- 5.2 数据的采集
- 5.3 数据的分析
- 5.4 数据的可视化表达
- 第六章 人工智能及其应用
- 项目范例 剖析空调企业智能客服机器人
- 6.1 认识人工智能
- 6.2 人工智能的应用
