七年级数学第一章有理数导学案(21课时)
文档属性
| 名称 | 七年级数学第一章有理数导学案(21课时) |  | |
| 格式 | zip | ||
| 文件大小 | 282.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-11-12 13:59:30 | ||
图片预览




文档简介
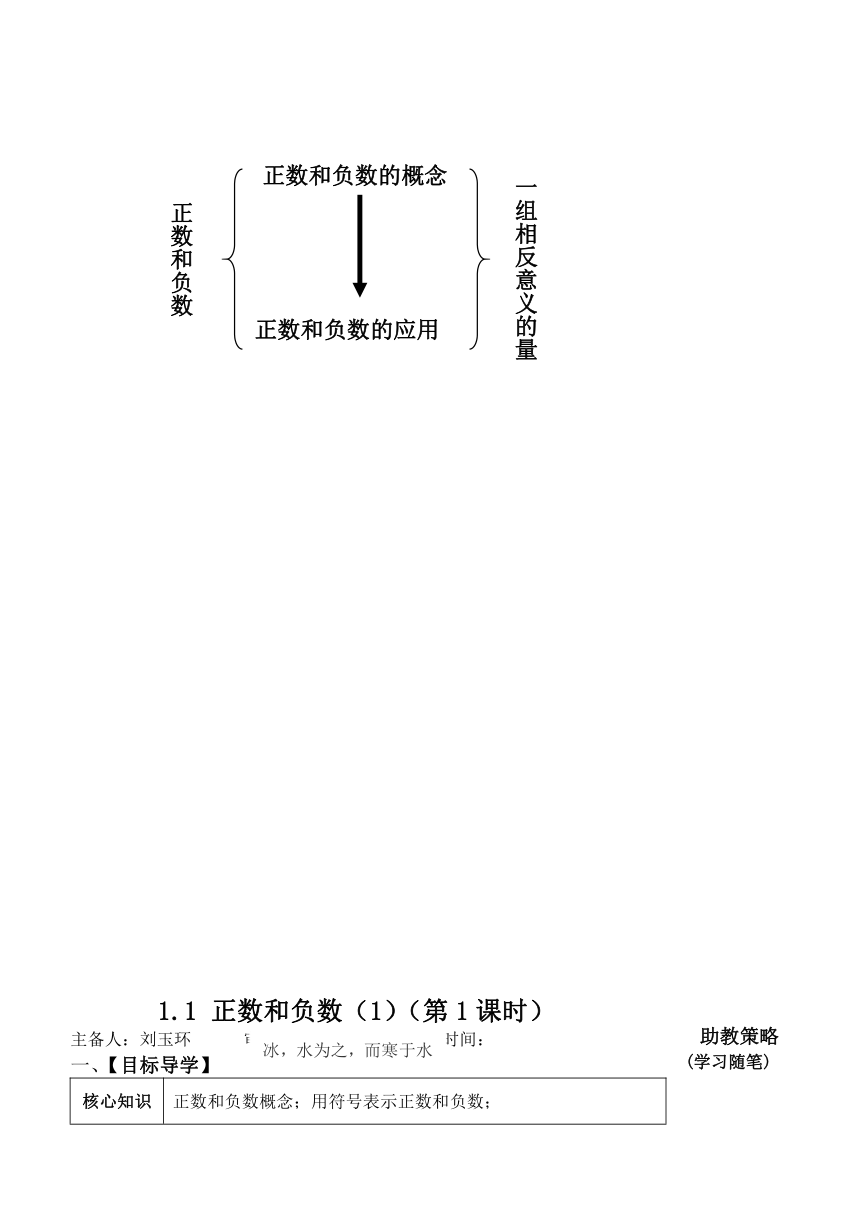
第一章 有理数知识框架图
1.1 正数和负数核心知识框架图
1.1 正数和负数(1)(第1课时)
主备人:刘玉环 审核人: 审核时间:
一、【目标导学】
核心知识 正数和负数概念;用符号表示正数和负数;
核心能力 会用正、负数表示具有相反意义的量;
情感态度 体验数学发展是生活实际的需要,激发学生学习数学的兴趣。
【学习重点】:两种意义相反的量
【学习难点】:正确会区分两种不同意义的量。
二、【自主学习】
1、正数与负数的产生
(1)生活中具有相反意义的量
如:运进5吨与运出3吨;上升7米与下降8米;向东50米与向西47米等都是生活中遇到的具有相反意义的量。
请你也举一个具有相反意义量的子: 。
(2)负数的产生同样是生活和生产的需要
2、正数和负数的表示方法
(1)活动:两个同学一组,一同学任意说意义相反的两个量,另一个同学用正负数表示.
(2)阅读P3练习前的内容
3、正数、负数的概念
1)大于0的数叫做 ,小于0的数叫做 。
2)正数是大于0的数,负数是 的数,0既不是正数也不是负数。
三、【合作探究】
1. P3第一题到第二题(直接做在课本上)。
2.小明的姐姐在银行工作,她把存入3万元记作+3万元,那么支取2万元应记作_______,-4万元表示________________。
3.已知下列各数:,,3.14,+3065,0,-239; 则正数有_________;负数有________。
4.下列结论中正确的是 …………………………………………( )
A.0既是正数,又是负数 B.O是最小的正数
C.0是最大的负数 D.0既不是正数,也不是负数
四、【展示质疑与小结】
五、【能力检测】
1.零下15℃,表示为_________,比O℃低4℃的温度是_________。
2.地图上标有甲地海拔高度30米,乙地海拔高度为20米,丙地海拔高度为-5米,其中最高处为_______地,最低处为_______地.
3.“甲比乙大-3岁”表示的意义是______________________。
4.甲冷库的温度是-12°C,乙冷库的温度比甲冷酷低5°C,则乙冷库的温度是
5.如果海平面的高度为0米,一潜水艇在海水下40米处航行,一条鲨鱼在潜水艇上方10米处游动,试用正负数分别表示潜水艇和鲨鱼的高度。
六、【课外拓展】
一种零件的内径尺寸在图纸上是9±0.05(单位:mm),表示这种零件的标准尺寸是9mm,加工要求最大不超过标准尺寸多少 最小不小于标准尺寸多少
七、【星级评价】
自评☆☆☆ 他评 ☆☆☆ 师评☆☆☆ 及时订正△
1.1 正数和负数(2)(第2课时)
主备人:刘玉环 审核人: 审核时间:
一、【目标导学】
核心知识 会用正、负数表示具有相反意义的量;
核心能力 通过正、负数学习,培养学生应用数学知识的意识;
情感态度 通过探究,渗透对立统一的辨证思想。
【学习重点】:用正、负数表示具有相反意义的量
【学习难点】:实际问题中的数量关系
二、【自主学习】
1、指出下列各数哪些是正数?哪些是负数?
-2,9/2,0,-3/7,10,3.14,-0.08.
2、一个月内,小明体重增加2kg,小华体重减少1kg,小强体重无变化,写出他们这个月的体重增长值;
3、2009年下列国家的商品进出口总额比上一年的变化情况是:
美国减少6.4%, 德国增长1.3%,
法国减少2.4%, 英国减少3.5%,
意大利增长0.2%, 中国增长7.5%.
写出这些国家2009年商品进出口总额的增长率.
三、【合作探究】
1、某药品的说明书上标明保存温度是(20±2)℃,由此可知在 ℃~ ℃范围内保存才合适.
2、“牛牛”饮料公司的一种瓶装饮料外包装上有“500±30(mL)”字样,请问“500±30(mL)”是什么含义?质检局对该产品抽查5瓶,容量分别为503mL,511mL,489mL,473mL,527mL ,问抽查产品的容量是否合格?
分析:500±30(mL)中,“500”指的是什么?“+30”是什么意思?“-30”是什么意思?
四、【展示质疑与小结】
五、【能力检测】
1、课本第4面练习.
2、一种零件的内径尺寸在图纸上是30±0.05(单位:毫米),表示这种零件的标准尺寸是30毫米,加工要求最大不超过标准尺寸___ ___毫米,最小不低于标准尺寸___ ___毫米.
3、21世纪第一年一些国家的服务出口额比上年的增长率如下:
美国 德国 英国 中国 日本 意大利
-3.4% -0.9% -5.3% 2.8% -7.3% 7.0%
这一年这六国中哪些国家的服务出口额增长了,哪些国家的服务出口额减少了?,哪国增长率最高,哪国增长率最低?
六、【课外拓展】
1、教科书5页习题4、5、:6、7题
2、10筐橘子,以每筐15㎏为标准,超过的千克数记作正数,不足的千克数记作负数。标重的记录情况如下:+1,-0.5,-0.5,-1,+0.5,-0.5,+0.5,+0.5,+0.5,-0.5。问这10筐橘子各重多少千克?总重多少千克?
3、一种零件的内径尺寸在图纸上是9±0.05(单位:mm),表示这种零件的标准尺寸是9mm,加工要求最大不超过标准尺寸多少 最小不小于标准尺寸多少
七、【星级评价】
自评☆☆☆ 他评 ☆☆☆ 师评☆☆☆ 及时订正△
1.2有理数核心知识框架图
1.2.1 有理数(第3课时)
主备人:刘玉环 审核人: 审核时间:
一、【目标导学】
核心知识 掌握有理数的概念,会对有理数按一定标准进行分类,
核心能力 了解分类的标准与分类结果的相关性,初步了解“集合”的含义;
情感态度 体验分类是数学上常用的处理问题方法。
【学习重点】:正确理解有理数的概念
【学习难点】:正确理解分类的标准和按照一定标准分类
二、【自主学习】
1、通过两节课的学习,,那么你能写出3个不同类的数吗 .(4名学生板书)
__________________________________________
2、P6练习(做在课本上)
三、【合作探究】
有理数的分类
小组中每人任意写出三个数,
问题1:观察这些数,我们将这些数做一下分类;该分为几类,又该怎样分呢?
分为 类,分别是:
引导归纳: 统称为整数, 统称为有理数。
问题2:我们是否可以把上述数分为两类 如果可以,应分为哪两类
归纳:所有的正数组成 集合,所有的负数组成 集合
问题3:把下列各数填入它所属于的集合的圈内:
15,-,-5,,,0.1,-5.32,-80,123,2.333.
正整数集合 负整数集合
正分数集合 负分数集合
四、【展示质疑与小结】
五、【能力检测】
1、下列各数,哪些是整数 哪些是分数 哪些是正数 哪些是负数
+7,-5, ,,79,0,0.67,,+5.1
2、把下列给数填在相应的大括号里:
-4,0.001,0,-1.7,15,.
正数集合{ …},负数集合{ …},
正整数集合{ …},分数集合{ …}
3、0是整数吗 自然数一定是整数吗 0一定是正整数吗 整数一定是自然数吗
六、【课外拓展】
图中两个圆圈分别表示正整数集合和整数集合,请写并填入两个圆圈的重叠部分.你能说出这个重叠部分表示什么数的集合吗
正数集合 整数集合
七、【星级评价】
自评☆☆☆ 他评 ☆☆☆ 师评☆☆☆ 及时订正△
1.2.2数轴(第4课时)
主备人:刘玉环 审核人: 审核时间:
一、【目标导学】
核心知识 掌握数轴概念,理解数轴上的点和有理数的对应关系;
核心能力 会正确地画出数轴,利用数轴上的点表示有理数;
情感态度 领会数形结合的重要思想方法。
【学习重难点】:数轴的概念和用数轴上的点表示有理数.
二、【自主学习】
看课本P7-9填空:
1、数轴的概念:
定义:规定了 、 和 的直线叫做数轴。
2、数轴的画法:
(1)画 、定原点,标出原点“O”.
(2)取原点向 方向为正方向,并标出箭头.
(3)选适当的长度作为单位长度,并标出…,-3,-2,-1,1,2, 3…各点,请同学们画一个数轴:
3、数轴定义的理解:
(1)规定了原点、正方向和单位长度的直线叫做 ,如图1所示.
(2)所有的有理数,都可以用数轴上的点表示.例如:
A点表示-4; B点表示 O点表示 D点表示
4、观察数轴可以知道:
(1)在数轴上表示的两数,右边的数总比左边的数 。
(2)由正、负数在数轴上的位置可知:正数都有大于 ,负数都小于 ,正数 一切负数。
三、【合作探究】
1、考考你:下列图形哪些是数轴?
2、 数轴上点A表示-3,
(1)在同一数轴上,点B表示-5,则A、B之间的距离是___,
(2) 在同一数轴上与点A相距5个单位的点表示的数是____
(3)点A到原点的距离是___
四、【展示质疑与小结】
1. 数轴有什么作用?2. 怎样画数轴?
五、【能力检测】
1、在数轴上,表示数-3,2.6,,0,,,-1的点中,在原点左边的点有 个。
2、在数轴上点A表示-4,如果把原点O向正方向移动1个单位,那么在新数轴上点A表示的数是( )
A.-5, B.-4 C.-3 D.-2
3、 (1)(请先在头脑中想象点的移动,尝试解决下面问题,然后再画图解答)一个点在数轴上表示的数是-5,这个点先向左边移动3个单位,然后再向右边移动6个单位,这时它表示的数是多少呢 如果按上面的移动规律,最后得到的点是2,则开始时它表示什么数
(2)你觉得数轴上的点表示数的大小与点的位置有关吗 为什么
六、【课外拓展】
教科书第15页习题5、6、7
七、【星级评价】
自评☆☆☆ 他评 ☆☆☆ 师评☆☆☆ 及时订正△
1.2.3 相反数(第5课时)
主备人:刘玉环 审核人: 审核时间:
一、【导学目标】
核心知识 借助数轴理解相反数的概念,会求一个数的相反数;
核心能力 养学生观察、猜想、归纳的能力,初步形成数形结合的思想。
情感态度 体验数学发展是生活实际的需要,激发学生学习数学的兴趣。
【学习重点】理解相反数的概念和求一个数的相反数
【学习难点】:相反数概念的理解。
二、【自主学习】
思考:1、数轴上与原点距离是2 的点有______个,这些点表示的数是_____
2、请两位同学背靠背,一个向左走5步,另一个向右走5步,如果向右走为正,向左、向右分别记作什么?
一般地,设a是一个正数,数轴上与原点的距离是a的点有___个,它们分别在原点的____,表示____和____,我们说这两点关于原点对称。
+3.6 和-3.6,6和-6 ,每对数,有什么相同和不同?
归纳:像+3.6和-3.6、6和-6、,只有____ 不同的两个数,叫互为相反数。其中一个叫另一个的相反数.
考考你:(1)-8的相反数是___, 7是____的相反数。
(2)a的相反数是_____.-a的相反数是____
(3) 怎样表示一个数的相反数?
归纳:在这个数的前面添上“-”,就可表示这个数的相反数。如12的相反数是____,-9的相反数是_____,如果在这个数的前面添上“+”表示____.
(4)互为相反数在轴上的位置有什么特点?
(5) 零的相反数是____.
三、【合作探究】
1 .判断下列说明是否正确
(1)-(-3)表示-3的相反数( ), (2)-2.5的相反数是2.5( )
(3)2.7与-3.7是互为相反数( ) (4)-π是相反数。( )
2 .分别写出下列各数的相反数:1.3 、-6
-0.2 、-(-3) 、π-1
3. 填空:(1) -(-0.8)=___, (2) –(-)=____,
(3) +(+4)=____, (4) –(-11)=_____
四、【展示质疑与小结】
五、【能力检测】
1、课本P10练习
2、填空:
①的相反数是 ; ② 的相反数是;
③若-x=10,则x的相反数在原点的 侧。
3、若 a 是负数,则 -a 是 ___数;若 -a 是负数,则 a 是______数.
六、【课外拓展】
1、化简下列各数中的符号:
(1) (2)-(+5)
(3) (4)
2、 填空:
(1)a-4的相反数是 ,3-x的相反数是 。
(2)是 的相反数。
(3)如果-a=-9,那么-a的相反数是 。
(4)若-(a-5)是负数,则a-5 0.
(5) 若是负数,则x+y 0.
3、 已知a、b在数轴上的位置如图所示。
在数轴上作出它们的相反数;
用“<”按从小到大的顺序将这两个数连接起来。
4、如果a-5与a互为相反数,求a.
七、【星级评价】
自评☆☆☆ 他评 ☆☆☆ 师评☆☆☆ 及时订正△
1.2.4绝对值(1)(第6课时)
主备人:刘玉环 审核人: 审核时间:
一、【目标导学】
核心知识 借助数轴,理解绝对值的概念,能求一个有理数的绝对值。
核心能力 会利用绝对值比较两个有理数的大小。
情感态度 经历将实际问题数学化的过程,感受数学与生活的关系,贯彻数形结合的思想。
【学习重点】:正确理解绝对值的概念,会求已知数的绝对值
【学习难点】:绝对值的几何意义,应用绝对值解决实际问题
二、【自主学习】
1、情境引入:两只小狗从同一点O出发,在一条笔直的街上跑,一只向右跑10米到达A点,另一只向左跑10米到达B点。
(1)若规定向右为正,则A处记做__________,B处记做__________;
(2)A处距离出发点“O” 米,B处距离出发点“O” 米;
(3)这两只小狗在跑的过程中,有没有共同的地方?
(4)在数轴上的A、B两点又有什么特征?
2、在数轴上找到-5和5的点,它们到原点的距离分别是多少?
3、绝对值的概念:在数轴上,一个数所对应的点与原点的距离叫做该数的 。用符号“ ”表示。例如:-5到原点的距离是 ,所以-5的绝对值是 ,记作:|-5|= ,5的绝对值是 ,记作 。
三、【合作探究】
如上图,学校位于数轴的原点处,小光、小明、小亮家分别位于点A、B、C处,单位长度表示1千米。小光家所在的位置对应的数是 ,与原点的距离是 ,那就是说,-2的绝对值是 ,记作= ;小明家所在的位置对应的数是 ,与原点的距离是 ,那就是说+1的绝对值是 1,记作 。
提问:互为相反数的两个数的绝对值有什么关系?
2、探索绝对值的性质:试一试,填空:
= ;= ;= ; = ;
提出问题:你能从上面的解答中发现什么规律吗?
总结:绝对值的性质:
(1)一个正数的绝对值等于 ;
(2)一个负数的绝对值等于它的 ;
(3)0的绝对值是 ;
(4)互为相反数的两个数的绝对值 。
四、【展示质疑与小结】
五、【能力检测】
1、课本P13习题第5、6、7题。
2、想一想:
(1)一个数的绝对值是它本身,这个数是什么数?
(2)一个数的绝对值是它的相反数,这个数是什么数?
【课外拓展】
1、用”>”、”<”、”=”连接下列两数:
∣∣___∣∣ ∣-3.5∣___-3.5
∣0∣____∣-0.58∣ ∣-5.9∣___∣-6.2∣
2、 数轴上与表示1的点的距离是2的点所表示的数有___________________.
3、 计算|4|+|0|-|-3|=______________.
4、绝对值的数学表示式:
七、【星级评价】
自评☆☆☆ 他评 ☆☆☆ 师评☆☆☆ 及时订正△
1.2.5有理数大小的比较(第7课时)
主备人:刘玉环 审核人: 审核时间:
一、【目标导学】
核心知识 借助数轴,理解有理数大小关系,会比较两个有理数的大小。
核心能力 能熟练运用法则结合数轴比较有理数的大小,特别是应用绝对值概念比较两个负数的大小,能利用数轴对多个有理数进行有序排列。
情感态度 转化思想[比较负数→比较正数
【学习重点】:会比较两个有理数的大小
【学习难点】:有理数大小比较法则中两个负数比较法则的理解
二、【自主学习】
问题一:3的绝对值是 ,-3的绝对值是 ;绝对值等于3的数是 ,0的绝对值是 ,
问题二:下面是某一天5个城市的最低气温:
哈尔滨-20℃、北京-10℃、长沙5℃、上海0℃、广州10℃
1、比较这一天下列两个城市间最低气温的高低(填“高于”或“低于”)
广州_______上海; 北京________哈尔滨;
武汉________哈尔滨; 武汉__________广州。
2、画一画:
(1)把上述5个城市最低气温的数表示在数轴上。
(2)观察这5个数在数轴上的位置,从中你发现了什么?
(3)温度的高低与相应的数在数轴上的位置有什么关系?
归纳: 在数轴上表示的两个数,右边的数总比左边的数 。
正数都大于 ,负数都小于 ,正数 负数。
三、【合作探究】
1、在数轴上表示数2,0,-3,-1,并比较它们的大小,将它们按从小到大的顺序用“<”号连接。
2、(1)求出数轴上各数的绝对值,并比较它们的大小.
(2)由上你发现了什么?
归纳: 两个正数比较大小,绝对值大的数 ;
两个负数比较大小,绝对值大的数反而 。
想一想:我们有几种方法来判断有理数的大小?你认为它们各有什么特点?
四、【展示质疑与小结】
五、【能力检测】
1、课本P13练习
2、课本P14-15习题第5,6、12题
3、(1) 整数x满足<3,则x=___________________,
(2)负整数x满足,则x=___________________
六、【课外拓展】
1.本节课主要学习了有理数大小比较的两种方法,一种是按照法则,两两比较,另一种是利用数轴,
2.绝对值比较时,分母相同,分子大的数 ;分子相同,则分母大的数反而 ;分子分母都不相同时,则应先通分再比较,或把分子化为相同再比较。
3.两个负数比较大小时的一般步骤:①求绝对值;②比较绝对值的大小;③比较负数的大小。
七、【星级评价】
自评☆☆☆ 他评 ☆☆☆ 师评☆☆☆ 及时订正△
1.3有理数的加、减法核心知识框架图
1.3.1有理数的加法(1)(第8课时)
主备人:刘玉环 审核人: 审核时间:
一、【目标导学】
核心知识 探索有理数加法法则,理解有理数的加法法则;
核心能力 能运用有理数加法法则,正确进行有理数加法运算;
情感态度 经历探索有理数加法法则的过程,体验数学来源于实践并为实践服务的思想,同时培养学生探究性学习的能力.
【学习重点】:有理数加法法则。
【学习难点】:异号两数相加的法则。
二、【自主学习】
1、比较大小:
(1)-π -3.14 (2)0.0001 -1000
看课本P19-20页填空:
1、有理数加法法则:
(1)、同号两数相加,取 的符号,并把 相加;
(2)、异号两数相加,取 符号,并用较 的绝对值减去较 的绝对值;
(3)、互为相反数的两个数相加得 ;
(4)、 一个数同0相加,仍得 。
三、【合作探究】
1、计算下列各式:
(1) (一8)+(一12); (2) (一3.75)+(-0.25);
(3)(一5)+9; (4)(-10)+7
(5)4+(-4) (6)(-9)+0
2、小慧原来在银行存有零用钱350元,上个月取出了120元,这个月计划再存人50元,请用有理数的加法计算:
(1)到上月底小慧在银行还有多少存款
(2)到这个月底小慧将有多少存款
四、【展示质疑与小结】
五、【能力检测】
1、课本P18练习
2、课本P24习题第1题
六、【课外拓展】
1.有理数的加法法则;
2.有理数加法的数轴表示;
3.有理数相加,先确定 ,再算绝对值;
4.有理数的加法运算,和不一定大于加数。
七、【星级评价】
自评☆☆☆ 他评 ☆☆☆ 师评☆☆☆ 及时订正△
1.3.1有理数的加法(二)(第9课时)
主备人:刘玉环 审核人: 审核时间:
一、【目标导学】
核心知识 进一步掌握有理数加法运算法则,理解加法运算律在有理数范围内推广的合理性;
核心能力 能运用加法运算律简化加法运算;
情感态度 经历有理数加法运算律的探索,体会观察、实践、归纳等活动在数学中的作用.
【学习重点】:运算律的理解及合理、灵活的运用。
【学习难点】:合理运用运算律。
二、【自主学习】
1、 计算下列各式:
(1)(+5)+(+8); (2)(-5)+(-8); (3)(+9)+(-2);
(4)(-9)+(+2); (5)(-9)+0; (6)0+0
2、计算下列各题:
(1) (-9.18)+6.18; (2) 6.18+(-9.18);
3、计算下列各题:
(1) [8+(-5)]+(-4); (2) 8+[(-5)+(-4)];
(3) [(-7)+(-10)]+(-11); (4) (-7)+[(-10)+(-11)];
(5) [(-22)+(-27)]+(+27); (6) (-22)+[(-27)+(+27)].
通过上面练习,观察得出:
交换律——两个有理数相加,交换加数的位置, 不变。
用代数式表示上面一段话:a+b=
结合律——三个数相加,先把前两个数相加,或者先把后两个数相加,和不变.用代数式表示上面一段话:(a+b)+c=
三、【合作探究】:
1、计算:(1) 33+(-2)+7+(-8) (2)4.375+(-82)+( -4.375)
小结:简化加法运算一般是三种方法:首先消去互为相反数的两数(其和为0),同号结合或凑整数。
四、【展示质疑与小结】
五、【能力检测】
1、课本P20练习:1、2
2、课本P24习题第2题
3、计算
(1) (2)(-9)+4+(-5)+8;
(3)(-36.35)+(-7.25)+26.35+(+7)
(4)
(5)
六、【课外拓展】
某出租车沿公路左右行驶,向左为正,向右为负,某天从A地出发后到收工回家所走的路线如下:(单位:千米)
⑴ 问收工时离出发点A多少千米?
⑵ 若该出租车每千米耗油0.3升,问从A地出发到收工共耗油多少升?
6.已知的相反数为-5,试求++(-)
7.计算:|1-|+|-|+|-|+…+|-|
七、【星级评价】
自评☆☆☆ 他评 ☆☆☆ 师评☆☆☆ 及时订正△
1.3.2有理数的减法(第10课时)
主备人:刘玉环 审核人: 审核时间:
一、【目标导学】
核心知识 理解有理数减法法则, 能熟练进行减法运算.
核心能力 会将减法转化为加法,进行加减混合运算,
情感态度 体会化归思想在数学中的作用.
【学习重点】:有理数减法法则和运算
【学习难点】:有理数减法法则的推导.
二、【自主学习】
1、填空:
(1)_______+6=20; (2)20+______=17;
(3)_______+(-2)=-20; (4)(-20)+____=-6?
2、学生独立看书,自学课本P.21~P.22
得出结论: 减去一个数等于加上这个数的_______ .
三、【合作探究】
1、 计算:
(1) 0-(-3.18) (2)(-10)-(-6) (3)-
2、某市元月中旬的平均气温是5℃,元月下旬因有寒流,预计气温将下降6~9℃,预计元月下旬的平均气温在什么范围内?
(理解、列式、计算)
总结反思:
(1) 有理数减法法则:减去一个数,等于加上这个数的 。
(2) 有理数减法的步骤:先变为 ,再改变 的符号,最后按有理数加法法则计算.
四、【展示质疑与小结】
五、【能力检测】
1.填空题:
(1)12-(+3)=___+___=___; (2)(-7)-(-6)=____+____=____;
(3)9-(-9)=____+____=___; (4)(-32)-(+13) ___+___=___.
2.计算:
(1)6-9; (2)(+4)-(-7); (3)(-5)-(-8);
(4) |-(-2.3)|-4.6; (5)1.9-(-0.6); (6)0-(-|5.4|)
3.计算
(1)比2℃低8℃的温度; (2)比-5℃低6℃的温度.
5.世界最高峰是珠穆朗玛峰,海拔高度是8848米,陆上最低处是位于亚洲西部的死海湖,湖面海拔高度是-392米,两处高度相差多少?
六、【课外拓展】
1.已知a = 8,b = -5,c = -3,求下列各式的值:
(1)a-b-c; (2)a-(c+b)
2.若a<0 , b>0, 则a, a+b, a-b, b中最大的是( )
A. a B. a+b C. a-b D. b
七、【星级评价】
自评☆☆☆ 他评 ☆☆☆ 师评☆☆☆ 及时订正△
1.3.2有理数的加、减法混合运算(第11课时)
主备人:刘玉环 审核人: 审核时间:
一、【目标导学】
核心知识 理解有理数减法法则, 能熟练进行减法运算.
核心能力 会将减法转化为加法,进行加减混合运算,
情感态度 体会化归思想在数学中的作用.
【学习重点】:有理数减法法则和运算
【学习难点】:有理数减法法则的推导.
二、【自主学习】
1、计算下列各式:
(1)(-18)-(-4); (2)(-18)-4; (3)(+18)-(-4)
2、请认真看课本第23页至24面的内容,要求解决两个问题:(1)有理数的加减混合运算与有理数的加法有什么联系?(2)有理数的加减混合运算有哪些步骤?
三、【合作探究】
(1)计算(-9)+(+6)-(-11)-7.(看到这个题目你想怎样做?你是怎么做的?)
若先把减法转化为加法,这时就成了___,___,___,___的和,正号通常可以省略,负号也可以通过化简省略,即
原式=________________________(省略正号并化简)
=_________________________(省略括号)
虽然加号、括号省略了,但-9+6+11-7仍表示-9,+6,+11,-7的和,所以这个算式可以读成什么?有哪两种读法?
(2)用加法运算律计算出结果
既然算式能看成几个数的和,我们可以运用加法的运算律进行计算,通常同号两数放在一起分别相加.
-9+6+11-7=(______)+(_______)
那么:-9+6+11-7接下来该怎样计算?
-9+6+11-7=________________=_______________=______
展示交流:全班合作交流,教师点拨后得出有理数加减混合运算的一般步骤:
(1)__________;(2)__________;(3)_________;(4)________;(5) __________
巩固练习:计算 (1)-4+7-4 (2)+6+9-15+31、
四、【展示质疑与小结】
1、 有理数减法法则:减去一个数,等于加上这个数的 。
2、 有理数减法的步骤:先变为 ,再改变 的符号,最后按有理数加法法则计算。
五、【能力检测】
1.填空题:
1.-4+7-4=-_____ - ______ + ________
2.+6+9-15+3=______________________
3.-9-3+2-4=_______9_______3_____4_____2
4.____________
2. 计算
(1)(+9)-(+10)+(-2)-(-8)+3; (2)
3.计算
(1)(+9)-(+10)+(-2)-(-8)+3 (2)
六、【课外拓展】
计算:(1)一天早晨的气温是-7℃,中午上升了11℃,半夜又下降了9℃,半夜的温度是多少?
(2)有8筐白菜,以每筐25千克为准,超过的千克数记作正数,不足的千克数记作负数,称后的记录如下:
1.5, -3.2, -0.5, 1, -2, -2, -2.5。 则这筐白菜一共多少千克?
七、【星级评价】
自评☆☆☆ 他评 ☆☆☆ 师评☆☆☆ 及时订正△
1.4有理数的乘、除法核心知识框架图
1.4.1有理数的乘法(1)(第12课时)
主备人:刘玉环 审核人: 审核时间:
一、【目标导学】
核心知识 掌握有理数乘法法则,初步了解有理数乘法法则的合理性。
核心能力 能够运用法则进行简单的有理数的乘法运算。
情感态度 通过对问题的变式探索,培养观察、归纳、猜测、验证能力。
【学习重点】:能按有理数乘法法则进行简单的有理数乘法运算。
【学习难点】:有理数乘法法则的推导。
1.了解有理数乘法的实际意义,理解有理数的乘法法则;
2. 能熟练地进行有理数的乘法运算.
二、【自主学习】
1.有理数加法法则内容是什么?
2.计算:
(1)2+2+2= (2)(-2)+(-2)+(-2)=
3.你能将上面两个算式写成乘法算式吗?
三、【合作探究】
1.自学课本28-29页回答下列问题
(1)如果它以每分2cm的速度向右爬行,3分钟后它在什么位置
可以表示为 .
(2)如果它以每分2cm的速度向左爬行,3分钟后它在什么位置
可以表示为
(3) 如果它以每分2cm的速度向右爬行,3分钟前它在什么位置
可以表示为
(4)如果它以每分2cm的速度向左爬行,3分钟前它在什么位置
可以表示为
由上可知:(1) 2×3 = ; (2)(-2)×3 = ;
(3)(+2)×(-3)= ; (4)(-2)×(-3)= ;
(5)两个数相乘,一个数是0时,结果为0
观察上面的式子, 你有什么发现?能说出有理数乘法法则吗?
归纳有理数乘法法则:
两数相乘,同号 ,异号 ,并把 相乘。
任何数与0相乘,都得 。
四、【展示质疑与小结】
五、【能力检测】
1.计算:
(1)0.25×(-4) (2)0×(-0.125) (3) (-)×(-0.5)
(4) (-)×6 (5)(-)×(-0.125) (6)(- 0.25) ×
2.对于有理数a、b定义一种运算:a*b=2a-b,计算(-2)*3+1
六、【课外拓展】
初一年级共100名学生,在一次数学测试中以90分为标准,超过的记为正,不足的记为负,成绩如下:
人数 10 20 5 14 12 18 10 4 9 6 2
成绩 -1 +3 -2 +1 +10 +2 0 -7 +7 -9 -12
请你算出这次考试的平均成绩.
七、【星级评价】
自评☆☆☆ 他评 ☆☆☆ 师评☆☆☆ 及时订正△
1.4.1有理数的乘法(2)(第13课时)
主备人:刘玉环 审核人: 审核时间:
一、【目标导学】
核心知识 经历探索多个有理数相乘的符号确定法则;
核心能力 会进行有理数的乘法运算;
情感态度 通过对问题的探索,培养观察、分析和概括的能力。
【学习重点】:多个有理数乘法运算符号的确定;
【学习难点】:正确进行多个有理数的乘法运算。
二、【自主学习】
1、有理数乘法法则:
2、计算:(1)(-0.75)×(-2)= (2)(-0.125)×8=
三、【合作探究】
观察:下列各式的积是正的还是负的?
2×3×4×(-5),
2×3×(-4)×(-5),
2×(-3)× (-4)×(-5),
(-2) ×(-3) ×(-4) ×(-5);
思考:几个不是0的数相乘,积的符号与负因数的个数之间有什么关系?
分组讨论交流,再用自己的语言表达所发现的规律:
几个不是0的数相乘,负因数的个数是 时,积是正数;负因数的个数是 时,积是负数。
例题:(1)
(2)
请你思考,多个不是0的数相乘,先做哪一步,再做哪一步?
你能看出下列式子的结果吗?如果能,理由
7.8×(-8.1)×O× (-19.6)
四、【展示质疑与小结】
五、【能力检测】
1、选择:(1).若干个不等于0的有理数相乘,积的符号( )
A.由因数的个数决定 B.由正因数的个数决定
C.由负因数的个数决定 D.由负因数和正因数个数的差为决定
2、下列运算结果为负值的是( )
A.(-7)×(-6) B.(-6)+(-4) C. 0×(-2)(-3) D.(-7)-(-15)
3、下列运算错误的是( )
A.(-2)×(-3)=6 B.
C.(-5)×(-2)×(-4)=-40 D.(-3)×(-2)×(-4)=-24
二、计算:
(1)、—5×8×(—7)×(—0.25);
(2);
六、【课外拓展】
(1)、 ;
(2)、 ;
七、【星级评价】
自评☆☆☆ 他评 ☆☆☆ 师评☆☆☆ 及时订正△
1.4.1有理数的乘法(3)(第14课时)
主备人:刘玉环 审核人: 审核时间:
一、【目标导学】
核心知识 通过自己动手实际操作,证明有理数运算中乘法的交换律、结合律以及分配律依然成立;
核心能力 通过对问题的探索,培养观察、分析和概括的能力。
情感态度 培养积极参与对数学问题的讨论的能力,敢于发表自己的观点,并用实例来给予证明,培养对数学的好奇心
【学习重点】:理解有理数乘法依然满足交换律、结合律与分配律,并会利用它们进行简化运算。
【学习难点】:运用乘法的交换律、结合律、分配律进行简化运算的原则。
二、【自主学习】
1、计算
(1)(-78)×5= (2)(-8)×(-2.5)=
2、做一做,并比较它们的结果。
(-2) ×7= , 7×(-2)=
(-3)×(-4)= ,(-4)×(-3)=
由上面的两组式子,我们发现乘法满足
[3×(-4)]×(-5)= ×(-5)=
3×[(-4)×(-5)]=3× =
由上面的两组式子,我们发现乘法满足
(-6)×[4+(-9)]=(-6)× =
(-6)×4+(-6)×(-9)= + =
由上面的两组式子,我们发现乘法满足
请用字母表示乘法的交换律、结合律与分配律:
乘法的交换律:
乘法的结合律:
乘法的分配律:
三、【合作探究】
1、计算:(1) (2)
2、某校体育器材室共有60个篮球。一天课外活动,有3个级分别计划借篮球总数的,和。请你算一算,这60个篮球够借吗?如果够了,还多几个篮球?如果不够,还缺几个?
四、【展示质疑与小结】
五、【能力检测】
1.运用运算律填空.
(1)-2×=×(_____).
(2)[×2]×(-4)=×[(______)×(______)].
(3)×[+]=×(_____)+(_____)×
2.选择题:利用分配律计算时,正确的方案是 ( )
A B
C D
3.运用运算律计算:
(1)(-25)×(-85)×(-4) (2) eq \b(--)×16
(3)60×-60×+60× (4)(—100)×(-+-0.1)
六、【课外拓展】
1. 已知:互为相反数,c、d互为倒数,x的绝对值是1,求:
3x—[(a+b)+cd]x的值
2. 定义一种运算符号△的意义:a△b=ab—1,求:
2△(—3)、2△[(—3)—5]的值
七、【星级评价】
自评☆☆☆ 他评 ☆☆☆ 师评☆☆☆ 及时订正△
1.4.2有理数的除法(第15课时)
主备人:刘玉环 审核人: 审核时间:
一、【目标导学】
核心知识 了解有理数除法的定义;理解倒数概念,会求有理数的倒数;
核心能力 掌握除法法则,会进行有理数的除法运算;
情感态度 培养积极参与对数学问题的讨论的能力,敢于发表自己的观点,并用实例来给予证明,培养对数学的好奇心
【学习重点】:正确进行有理数除法的运算,正确求一个有理数的倒数
【学习难点】:如何进行有理数除法的运算,求一个负数的倒数。
二、【自主学习】
1、 (-2) × 8 = 7×(-3)=
(-3)×(-5)= (-4)×(-3)=
×( )=1; 0.5×( )=1;
-4×( )=1; ×( )=1.
2、(1)6个同样大小的苹果平均分给3个小孩,每个小孩分到几个苹果?
(2)怎样计算下列各式? (独立思考后,再将结果与同桌交流)
(-6)÷3 6÷(-3) (-6)÷(-3) 0÷4
归纳:同号两数相除得( ),异号两数相除得( )并且把它们的( )相除0除以以何一个不为等于0的数都得( )
2、比较下列各组数的计算结果
(1) 1÷5 与1× (2)2÷() 与 2×
归纳:如果两个数的乘积等于1,那么把其中一个数叫做另一个数的( ),也称这两个数( )。除以一个非零数等于乘上这个数的( )
三、【合作探究】
1、(1)(-18)÷6= (2)(-63)÷(-7)=
(3)0÷(-8)= (4)16÷(-3)=
2、-6的倒数是________ -6 的倒数的倒数是________
-6 的相反数是________ -6 的相反数的相反数是________
四、【展示质疑与小结】
五、【能力检测】
1、(1)()÷()= ( 2)(-6.5)÷0.13 =
(3)()÷()= (4)÷(-1)=
(5)的倒数是 (6) 的相反数是
3、1.4的倒数是 ; 若a,b互为倒数,则2ab= ;
4、若一个数和它的倒数相等,则这个数是 ;若一个数和它的相反数相等,则这个数是 ;
六、【课外拓展】
1.果两个有理数的和除以它们的积,所得的商是0,那么这两个有理数 ( )
A.互为相反数,但不等于0 ; B.互为倒数 ; C.有一个等于0 ; D.都等于0
2.b≠0,则+的取值不可能是 ( )
A.0 B.1 C.2 D.-2
3.++=1,求()2003÷(××)的值。
七、【星级评价】
自评☆☆☆ 他评 ☆☆☆ 师评☆☆☆ 及时订正△
1.4.2有理数的运算顺序(第16课时)
主备人:刘玉环 审核人: 审核时间:
一、【目标导学】
核心知识 掌握有理数加、减、乘、除运算顺序
核心能力 会正确合理地进行有理数运算;
情感态度 培养学生严谨的学习习惯。
【学习重点】:正确进行有理数的混合运算。
【学习难点】:正确合理地进行运算。
二、【自主学习】
一、自主学习
1、计算
(1) (-8)÷(-4); (2) (-9)÷3 (3) (—0.1)÷×(—100);
2. 有理数的除法法则
3、 计算
(1)(—8)+4÷(-2) (2)(-7)×(-5)—90÷(-15)
你的计算方法是先算 法,再算 法。
有理数加减乘除的混合运算顺序应该是 写出解答过程
2.自学完成例9(阅读课本P36—P37页内容)
三、【合作探究】
1、计算(P36练习)
(1)6—(—12)÷(—3);(2)(—48)÷8—(—25)×(—6);
( 3);
四、【展示质疑与小结】
五、【能力检测】
1、选择题
(1)下列运算有错误的是( )
A.÷(-3)=3×(-3) B.
C.8-(-2)=8+2 D.2-7=(+2)+(-7)
(2)下列运算正确的是( )
A. ; B.0-2=-2; C. D.(-2)÷(-4)=2;
2、计算
1)、18—6÷(—2)× ; 2)11+(—22)—3×(—11);
六【课外拓展】
(1) (-)÷(-)÷(-) (2)
(3) (4)
七、【星级评价】
自评☆☆☆ 他评 ☆☆☆ 师评☆☆☆ 及时订正△
1.5有理数的乘方核心知识框架图
1.5.1有理数的乘方(第17课时)
主备人:刘玉环 审核人: 审核时间:
一、【目标导学】
核心知识 理解乘方的意义,探究有理数乘方的符号法则;
核心能力 会正确进行有理数乘方运算。
情感态度 经历探索有理数乘方的运算,获得解决问题经验。
【学习重点】:有理数乘方的意义以及有理数乘方的运算
【学习难点】:有理数乘方运算以及符号法则
二、【自主学习】
1、复习巩固:
①乘法运算的符号法则及运算方法:
②多个不为0的数相乘,积的符号怎样确定?
2、导学:
(1)一般地,几个相同因数相乘,即,记作 ,读作
求n个相同因数的 ,叫作乘方,乘方的结果叫做 。 在中,叫做 ,叫作 。当看作的次方的结果时,也可读作 。
特别地一个数也可以看作这数本身的一次方,如5就是5的一次,即,指数为1通常 不写。
(2)警示:
①乘方是一种运算(乘法运算的特例),即求个相同因数连乘的简便形式;
②幂是乘方的结果,它不能单独存在,即没有乘方就无所谓幂;
③乘方具有双重含义:既表示一种 ,又表示乘方运算的结果;
④书写格式:若底数是负数、分数或含运算关系的式子时,必须要用 把底数括起来,以体现底数的整体性。
(3)拓展:底数为,0,1,10,0.1的幂的特性:
(n为正整数) (n为整数)
(1后面有____个0), =0.00…01 (1前面有______个0)
(4)乘方的符号法则:
负数的奇次幂是 数,负数的偶次幂是 数。
正数的任何次幂都是 数,0的任何正整数次幂都是 。
三、【合作探究】
1、计算:
, , , ,
, ,
2、 ;
3、已知n是正整数,那么 , 4、如果一个有理数的偶次幂是非负数,那么这个有理数是 。
A、正数 B、负数 C、0 D、任何有理数
5、平方等于9的数是 ,立方等于27的数是 ,平方等于本身的数是 ,立方等于本身的数是
四、【展示质疑与小结】
五、【能力检测】
1、把写成乘方形式 。
2、计算: , ,
3、若,则 若,则
六、【课外拓展】
1、计算:
2、观察下列数,根据规律写出横线上的数
;;;;______;第2010个数是____________。
七、【星级评价】
自评☆☆☆ 他评 ☆☆☆ 师评☆☆☆ 及时订正△
1.5.1有理数的乘方(第18课时)
主备人:刘玉环 审核人: 审核时间:
一、【目标导学】
核心知识 能确定有理数加、减、乘、除、乘方混合运算的顺序;
核心能力 及时纠正运算中的错误,进一步培养学生正确迅速的运算能力。
情感态度 培养学生严谨的学习态度。
【学习重点】:有理数的混合运算;
【学习难点】:运算顺序的确定和性质符号的处理。
二、【自主学习】
(一)复习回顾:
1、有理数的加、减、乘、除及乘方的运算法则
2、加入乘方后,有理数的混合运算的顺序如何?
(二)导学:
有理数的混合运算顺序:(1)先 ,再 ,最后 ;(2)同级运算,从左到右进行;(3)如有括号,先做 的运算,按小括号、中括号、大括号依次进行。
方法规律:
(1)有理数运算分三级运算,加减法是第一级运算,乘除法是第二级运算,乘方和开方(以后学习)是第 级运算。
运算顺序是:先算高级运算,再算 运算;同级运算,再按从左至右的顺序运算。
(2)在运算过程中注意运算律的运用
(三)完成P43例3及P44的练习
三、【合作探究】
1、计算:
(1)
(2)
(3)
2、观察下面行数:
① -3,9,-27,81,-243,729,…
② 0,12,-24,84,-240,732,…
③ -1,3,-9,27,-81,243,…
(1)第①行数有什么规律?
(2)第②行数与第①行数有什么关系?
(3)第③行数与第①行数有什么关系?
(3)取每行数的第10个数,计算这三个数的和
四、【展示质疑与小结】
五、【能力检测】
1、计算:
2、、为有理数,且,求的值;
4、一根1米长的绳子,第一次剪去,第二次剪去剩下的,如此剪下去,第六次后剩下的绳子还有1厘米长吗?为什么?
六、【课外拓展】
已知
试求的值
七、【星级评价】
自评☆☆☆ 他评 ☆☆☆ 师评☆☆☆ 及时订正△
1.5.2科学计数法(第19课时)
主备人:刘玉环 审核人: 审核时间:
一、【目标导学】
核心知识 了解科学记数法的意义,弄清科学记数法中10的指数n与这个数的整数位数的关系。
核心能力 会用科学记数表示绝对值大于10的数;
情感态度 体会科学记数法的优点。
【学习重点】:用科学记数法表示绝对值大于10的数;
【学习难点】:正确使用科学记数法表示数
二、【自主学习】
1、展示你收集的你认为非常大的数,与同学交流,你觉得记录这些数据方便吗?
2、现实生活中,我们会遇到一些比较大的数,如太阳的半径、光速,日前世界人口等,读写这样大的数有一定的困难,先看10的乘方的特点:
1000 000 1000 000 000
10…..0(在1后面有 个0)
对于一般的大数如何简单地表示出来?
3000 000 000 1000 000 000
696000 100 000
读作6.96乘10的5次方(幂)
3、科学记数法:
像上面这样,把一个大于10的数表示成 的形式(其中是整数数位只有一位的数,n是整数),使用的是科学记数法,“科学记数”谨记三点:
(1)弄清a×中的a的取值范围
(2)正确确定a×中的n的值,当所记数大于10时,n是 且等于所记数的整数位数 。
(3)会将用科学记数法表示的数还原。
提醒:a符号与原数的符号相同,如:将科学记数时,a为而不是。
三、【合作探究】
1、用科学记数法表示下列各数:
1000 000; 572 000 000; 123 000 000 000;
; ;
2、第五次人口普查知山西省人口总数约为3297万人,用科学记数法表示是多少人?
3、太阳直径为千米,其原数为多少米?
四、【展示质疑与小结】
五、【能力检测】
1、用科学记数法表示下列各数
10000; 800000; 567000; 000;
2、下列用科学记数法写出的数,原数分别是什么数?
4.5 7.04 3.96
3、下列各数,属于科学记数法表示的是 。
A、53.7 B、0.537 C、537 D、5.37
4、在比例尺为1:8000 000的地图上,量得太原到北京的距离为6.4㎝,将实际距离用科学记数法表示为 ㎞。
六、【课外拓展】
地球绕太阳公转的速度约为1.1㎞/h,声音在空气中传播速度为330m/s,试比较这两个速度的大小。
七、【星级评价】
自评☆☆☆ 他评 ☆☆☆ 师评☆☆☆ 及时订正△
1.5.3近似数(第20课时)
主备人:刘玉环 审核人: 审核时间:
一、【目标导学】
核心知识 了解近似数和有效数字的概念,
核心能力 能按要求取近似数和保留有效数字;
情感态度 体会近似数的意义及在生活中的应用。
【学习重点】:能按要求取近似数和有效数字;
【学习难点】:有效数字概念的理解。
二、【自主学习】
1.用科学记数法表示下列各数:
(1)1250000000= ;(2)-130000= ;
(3)-1025000= ;
2.下列用科学记数法表示的数,把原数写在横线上:
(1) ;(2)
三、【合作探究】
1.(1)我们班有 名学生, 名男生, 名女生;
(2)一天有 小时,一小时有 分,一分钟有 秒;
(3)我的体重约为 千克,我的身高约为 厘米;
(4)我国大约有 亿人口.
在上题中,第 题中的数字是准确的,第 题中的数字是与实际接近的。这种只是接近实际数字,但与实际数字还有差别的数被称为近似数。
2.你还能举出生活中的准确数与近似数吗?请将你举的例子写在下面的空白处。
3.近似数与准确数的接近程度,可以用精确度表示(就是按四舍五入保留小数)。
按四舍五入对圆周率取近似数时,有:
(精确到个位),
(精确到 0.1 ,或叫精确到十分位),
(精确到 ,或叫精确到 位),
(精确到 ,或叫精确到 位),
(精确到 ,或叫精确到 位)。……
4.例6按括号内的要求,用四舍五入法对下列各数取近似数:
(1)0.0158(精确到0.001); (2)304.35(精确到个位);
(3)1.804(精确到0.1); (4)1.804(精确到0.01);
解:(1) (2)
(3) (4)
思考:1.8,与1.80的精确度相同吗?在表示近似数时,能将小数点后的0随便去掉吗?
归纳:从一个数的左边________________, 到_______________止,所有的数字都是这个数的有效数字。
四、【展示质疑与小结】
五、【能力检测】
P46练习
用四舍五入法对它们取近似数,并写出各近似数数的有效数字
(1)0.00356(精确到万分位); (2)61.235(精确到个位);
(3)1.8935(精确到0.001); (4)0.0571(精确到0.1);
六、【课外拓展】
P47 T 6、9、10
七、【星级评价】
自评☆☆☆ 他评 ☆☆☆ 师评☆☆☆ 及时订正△
单元小结(第21课时)
主备人:刘玉环 审核人: 审核时间:
一、【目标导学】
核心知识 、复习整理有理数有关概念和有理数运算法则,运算律以及近似计算等有关知识;
核心能力 培养学生综合运用知识解决问题的能力;
情感态度 渗透数形结合的思想。
【学习重点】:有理数概念和有理数运算;
【学习难点】:负数和有理数法则的理解。
二、【自主学习】
2、知识专题部分:
专题1加法的运算律例1:计算:
专题2乘法的运算律及分配律
例2:计算:
专题3 充分利用概念
例3:已知a.b互为相反数,c.d互为倒数,m是绝对值最小的数,求代数式的值。
专题4 非负数性质的应用
例4:已知,求的值。
专题5 数形结合的思想方法
例5:有理数a.b在数轴上的位置如图所示 ,试比较:,,,这四个数的大小
专题6 公式的递用解题法
例6:计算: ①; ②
专题7 分类讨论的思想方法
例7:已知a是任一有理数,试比较与的大小.
专题8 特殊值法
例8:若,,且,则 0(填“”或“”)
三、【合作探究】
1、计算:
(1) (2)、
2、若m、n互为相反数,x、y互为倒数,求的值。
3、若与互为相反数,求的值。
4、已知有理数a、b、c在数轴上的位置,如图所示,化简.
四、【展示质疑与小结】
全章复习的目的是使学生进一步系统掌握基础知识、基本技能和基本方法,进一步提高综合运用数学知识灵活地分析和解决问题的能力?因此,我们应注意下面两个方面:第一,既加强基础,又提高能力和发展智力;第二,既全面复习,又突出重点?。
五、【能力检测】
1、写出下列各数的相反数和倒数?
原 数 5 -6 1 0?5 -1
相反数
倒 数
2、?计算:
(1); (2)(-81)÷÷(-16);
(3)22+(-2)3×5-(-0.28)÷(-2)2 (4)[(-3)3-(-5)3]÷[(-3)-(-5)]?
六、【课外拓展】
1、计算:
2、计算:
3、试比较与的大小。
七、【星级评价】
评☆☆☆ 他评 ☆☆☆ 师评☆☆☆ 及时订正△
青,取之于蓝,而青于蓝
正数和负数的概念
一组相反意义的量
正数和负数
正数和负数的应用
冰,水为之,而寒于水
助教策略
(学习随笔)
引导学生思考讨论,借助举例说明。
阅读思考。
方法指导:先独立完成,然后组内小展示时组长帮助组员学会。
1、本节课你有那些收获?
2、还有没解决的问题吗?
木直中绳,輮以为轮,其曲中规,虽有槁暴,不复挺者,輮使之然也
助教策略
(学习随笔)
方法指导:独立完成后,小组内的对子间互相用红笔互改,有疑问的由组长组织讨论订正。
故木受绳则直,金就砺则利,君子博学而日参省乎己,则知明而行无过矣
助教策略
(学习随笔)
通过上节课的学习,我们知道在实际生产和生活中存在着两种不同意义的量,为了区分它们,我们用正数和负数来分别表示它们.
通过问题3提醒学生审题时要注意要求,题中求的是增长率,不是增长值.
1、本节课你有那些收获?
2、还有没解决的问题吗?
吾尝跂而望矣,不如登高之博见也
教策略
(学习随笔)
方法指导:独立完成后,小组内的对子间互相用红笔互改,有疑问的由组长组织讨论订正。)
不临深溪,不知地之厚也
按整数、分数分:
按正数、负数、零分:
有理数的分类
意义:
在数轴上表示:
相反数
有理数
在数轴上:
利用绝对值:
有理数的大小比较方法
几何意义:
代数意义:
绝对值:
倒数意义:
行衢道者不至,事两君者不容。
助教策略
(学习随笔)
问题3中,首先要解释集合的含义.练习2中可补充思考:四个集合合并在一起是什么集合 (若降低难度可分开问)
不闻先王之遗言,不知学问之大也
助教策略
(学习随笔)
此题是一个探索题,有一定难度,可以分步完成,不如先写出正数,在写出整数,观察都具备的是其中哪个数.
蓬生麻中,不扶而直;
助教策略
(学习随笔)
学生观察,思考,研究,表示.增强学生的合作意识.
满足的条件可以先不必明确,基本能明确就可以,在后面逐步明
明确数轴的正确画法和要求.
练习中注意纠正学生数轴画法的错误和点的表示错误
白沙在涅,与之俱黑
助教策略
(学习随笔)
总结可以由教师提出问题,学生总结,教师完善
2题也可以启发学生反过来想,即点A向正方向移动1个单位.
3题有一定的难度,两次变动可转化成原点实际怎样移动了,移动了几个单位,那么-5实际上怎样移动了
干、越、夷、貉之子,生而同声,长而异俗,教使之然也
助教策略
(学习随笔)
知识回顾,导入新课。
观察、 归纳,提升学生发现问题的能力
物类之起,必有所始。
助教策略
(学习随笔)
神莫大于化道,福莫长于无祸
小节:相反数的概念及注意事项
助教策略
(学习随笔)
登高而招,臂非加长也,而见者远
助教策略
(学习随笔)
以开放的形式创设情境,以学生进行讨论,并培养分类的能力,培养学生的观察与归纳能力,渗透数形思想
方法指导:先独立完成,然后组内小展示时组长帮助组员学会。
登高而招,臂非加长也,而见者远
助教策略
(学习随笔)
方法指导:独立完成后,小组内的对子间互相用红笔互改,有疑问的由组长组织讨论订正。
顺风而呼,声非加疾也,而闻者彰
助教策略
(学习随笔)
方法指导:独立完成自主学习
方法指导:先独立完成,然后组内小展示时组长帮助组员学会。
假舆马者,非利足也,而致千里
0
1
-1
-2
2
0
1
-1
-2
2
助教策略
(学习随笔)
0
1
-1
-2
2
本节课我们学习了哪些内容?
方法指导:独立完成后,小组内的对子间互相用红笔互改,有疑问的由组长组织讨论订正。
假舟楫者,非能水也,而绝江河
有理数的加
、
减运算
法则
加法法则
减法法则
有理数加、减混合运算法则
运算律
加法交换律
字母表示:
文字叙述:
加法结合律
字母表示:
文字叙述:
简便计算
声无小而不闻,行无隐而不形 。
助教策略
(学习随笔)
方法指导:独立完成自主学习
方法指导:先独立完成,然后组内小展示时组长帮助组员学会。
君子生非异也,善假于物也
助教策略
(学习随笔)
本节课我们学习了哪些内容?
方法指导:独立完成后,小组内的对子间互相用红笔互改,有疑问的由组长组织讨论订正。
物类之起,必有所始
助教策略
(学习随笔)
方法指导:独立完成自主学习
荣辱之来,必象其德
助教策略
(学习随笔)
方法指导:先独立完成,然后组内小展示时组长帮助组员学会。
本节课我们学习了哪些内容?
方法指导:独立完成后,小组内的对子间互相用红笔互改,有疑问的由组长组织讨论订正。
肉腐出虫,鱼枯生蠹
助教策略
(学习随笔)
荣辱之来,必象其德
助教策略
(学习随笔)
方法指导:独立完成自主学习
方法指导:先独立完成,然后组内小展示时组长帮助组员学会。
怠慢忘身,祸灾乃作
助教策略
(学习随笔)
本节课我们学习了哪些内容?
方法指导:独立完成后,小组内的对子间互相用红笔互改,有疑问的由组长组织讨论订正。
强自取柱,柔自取束。
助教策略
(学习随笔)
方法指导:独立完成自主学习
方法指导:先独立完成,然后组内小展示时组长帮助组员学会。
白沙在涅,与之俱黑
助教策略
(学习随笔)
本节课我们学习了哪些内容?
方法指导:独立完成后,小组内的对子间互相用红笔互改,有疑问的由组长组织讨论订正。
草木畴生,禽兽群焉,物各从其类也。
乘法法则
除法法则
有理数乘、除混合运算法则
法则
有理数的乘
、
除运算
字母表示:
文字叙述:
乘法交换律
简便计算
运算律
字母表示:
文字叙述:
乘法结合律
字母表示:
文字叙述:
乘法分配律
玉在山而草润,渊生珠而崖不枯。
助教策略
(学习随笔)
方法指导:独立完成自主学习
方法指导:先独立完成,然后组内小展示时组长帮助组员学会。
是故质的张,而弓矢至焉;林木茂,而斧斤至焉
助教策略
(学习随笔)
本节课我们学习了哪些内容?
方法指导:独立完成后,小组内的对子间互相用红笔互改,有疑问的由组长组织讨论订正。
邪秽在身,怨之所构
助教策略
(学习随笔)
方法指导:独立完成自主学习
方法指导:先独立完成,然后组内小展示时组长帮助组员学会。
施薪若一,火就燥也,平地若一,水就湿也
助教策略
(学习随笔)
本节课我们学习了哪些内容?
方法指导:独立完成后,小组内的对子间互相用红笔互改,有疑问的由组长组织讨论订正。
积土成山,风雨兴焉
助教策略
(学习随笔)
方法指导:独立完成自主学习
方法指导:先独立完成,然后组内小展示时组长帮助组员学会。
积水成渊,蛟龙生焉
助教策略
(学习随笔)
本节课我们学习了哪些内容?
方法指导:独立完成后,小组内的对子间互相用红笔互改,有疑问的由组长组织讨论订正。
积善成德,而神明自得,圣心备焉
助教策略
(学习随笔)
方法指导:独立完成自主学习
方法指导:先独立完成,然后组内小展示时组长帮助组员学会。
故不积跬步,无以至千里
助教策略
(学习随笔)
本节课我们学习了哪些内容?
方法指导:独立完成后,小组内的对子间互相用红笔互改,有疑问的由组长组织讨论订正。
不积小流,无以成江海
助教策略
(学习随笔)
方法指导:独立完成自主学习
方法指导:先独立完成,然后组内小展示时组长帮助组员学会。
本节课我们学习了哪些内容?
其数则始乎诵经,终乎读礼
助教策略
(学习随笔)
方法指导:独立完成后,小组内的对子间互相用红笔互改,有疑问的由组长组织讨论订正。
骐骥一跃,不能十步
有理数的乘方运算法则
运算顺序
运算律的应用
有理数的乘方运算
有理数混合运算法则
科学记数法:a
近似数与有效数字的意义
玉在山而草润,渊生珠而崖不枯。
助教策略
(学习随笔)
方法指导:独立完成自主学习
n为奇数
n为偶数
锲而舍之,朽木不折
助教策略
(学习随笔)
方法指导:先独立完成,然后组内小展示时组长帮助组员学会。
本节课我们学习了哪些内容?
方法指导:独立完成后,小组内的对子间互相用红笔互改,有疑问的由组长组织讨论订正。
邪秽在身,怨之所构。
助教策略
(学习随笔)
方法指导:独立完成自主学习
方法指导:先独立完成,然后组内小展示时组长帮助组员学会。
伯牙鼓琴,而六马仰秣
助教策略
(学习随笔)
本节课我们学习了哪些内容?
方法指导:独立完成后,小组内的对子间互相用红笔互改,有疑问的由组长组织讨论订正。
故声无小而不闻,行无隐而不形
助教策略
(学习随笔)
方法指导:独立完成自主学习
方法指导:先独立完成,然后组内小展示时组长帮助组员学会。
玉在山而草润,渊生珠而崖不枯
助教策略
(学习随笔)
本节课我们学习了哪些内容?
方法指导:独立完成后,小组内的对子间互相用红笔互改,有疑问的由组长组织讨论订正。
为善不积邪?安有不闻者乎
助教策略
(学习随笔)
方法指导:独立完成自主学习
方法指导:先独立完成,然后组内小展示时组长帮助组员学会。
故学数有终,若其义则不可须臾舍也
本节课我们学习了哪些内容?
方法指导:独立完成后,小组内的对子间互相用红笔互改,有疑问的由组长组织讨论订正。
为之,人也;舍 之,禽兽也
助教策略
(学习随笔)
鼓励学生独立思考回答以上问题。组织学生讨论交流,梳理本章内容。
有理数
有理数的分类
按整数、分数分:
按正数、负数、零分:
意义:
在数轴上表示:
相反数
倒数意义:
有理数的大小比较方法
运算
在数轴上:
利用绝对值:
绝对值:
1、几何意义:
2、代数意义:
概念
法则
加法法则
减法法则
乘法法则
除法法则
乘方法则
有理数混合运算法则
运算律
交换律
1、加法交换律
2、乘法交换律
字母表示:
文字叙述:
字母表示:
文字叙述:
结合律
1、加法结合律
2、乘法结合律
字母表示:
文字叙述:
字母表示:
文字叙述:
分配律
字母表示:
文字叙述:
3、科学记数法的意义:
4、近似数与有效数字的意义:
驽马十驾,功在不舍
先组织学生独立尝试,再小组展示质疑。
. . .
a o b
为善不积邪?安有不闻者乎
学生独立解决问题。然后小组交流,弄清疑点,注意纠错。
为善不积邪?安有不闻者乎
助教策略
(学习随笔)
方法指导:独立完成后,小组内的对子间互相用红笔互改,有疑问的由组长组织讨论订正。
故不登高山,不知天之高也
1.1 正数和负数核心知识框架图
1.1 正数和负数(1)(第1课时)
主备人:刘玉环 审核人: 审核时间:
一、【目标导学】
核心知识 正数和负数概念;用符号表示正数和负数;
核心能力 会用正、负数表示具有相反意义的量;
情感态度 体验数学发展是生活实际的需要,激发学生学习数学的兴趣。
【学习重点】:两种意义相反的量
【学习难点】:正确会区分两种不同意义的量。
二、【自主学习】
1、正数与负数的产生
(1)生活中具有相反意义的量
如:运进5吨与运出3吨;上升7米与下降8米;向东50米与向西47米等都是生活中遇到的具有相反意义的量。
请你也举一个具有相反意义量的子: 。
(2)负数的产生同样是生活和生产的需要
2、正数和负数的表示方法
(1)活动:两个同学一组,一同学任意说意义相反的两个量,另一个同学用正负数表示.
(2)阅读P3练习前的内容
3、正数、负数的概念
1)大于0的数叫做 ,小于0的数叫做 。
2)正数是大于0的数,负数是 的数,0既不是正数也不是负数。
三、【合作探究】
1. P3第一题到第二题(直接做在课本上)。
2.小明的姐姐在银行工作,她把存入3万元记作+3万元,那么支取2万元应记作_______,-4万元表示________________。
3.已知下列各数:,,3.14,+3065,0,-239; 则正数有_________;负数有________。
4.下列结论中正确的是 …………………………………………( )
A.0既是正数,又是负数 B.O是最小的正数
C.0是最大的负数 D.0既不是正数,也不是负数
四、【展示质疑与小结】
五、【能力检测】
1.零下15℃,表示为_________,比O℃低4℃的温度是_________。
2.地图上标有甲地海拔高度30米,乙地海拔高度为20米,丙地海拔高度为-5米,其中最高处为_______地,最低处为_______地.
3.“甲比乙大-3岁”表示的意义是______________________。
4.甲冷库的温度是-12°C,乙冷库的温度比甲冷酷低5°C,则乙冷库的温度是
5.如果海平面的高度为0米,一潜水艇在海水下40米处航行,一条鲨鱼在潜水艇上方10米处游动,试用正负数分别表示潜水艇和鲨鱼的高度。
六、【课外拓展】
一种零件的内径尺寸在图纸上是9±0.05(单位:mm),表示这种零件的标准尺寸是9mm,加工要求最大不超过标准尺寸多少 最小不小于标准尺寸多少
七、【星级评价】
自评☆☆☆ 他评 ☆☆☆ 师评☆☆☆ 及时订正△
1.1 正数和负数(2)(第2课时)
主备人:刘玉环 审核人: 审核时间:
一、【目标导学】
核心知识 会用正、负数表示具有相反意义的量;
核心能力 通过正、负数学习,培养学生应用数学知识的意识;
情感态度 通过探究,渗透对立统一的辨证思想。
【学习重点】:用正、负数表示具有相反意义的量
【学习难点】:实际问题中的数量关系
二、【自主学习】
1、指出下列各数哪些是正数?哪些是负数?
-2,9/2,0,-3/7,10,3.14,-0.08.
2、一个月内,小明体重增加2kg,小华体重减少1kg,小强体重无变化,写出他们这个月的体重增长值;
3、2009年下列国家的商品进出口总额比上一年的变化情况是:
美国减少6.4%, 德国增长1.3%,
法国减少2.4%, 英国减少3.5%,
意大利增长0.2%, 中国增长7.5%.
写出这些国家2009年商品进出口总额的增长率.
三、【合作探究】
1、某药品的说明书上标明保存温度是(20±2)℃,由此可知在 ℃~ ℃范围内保存才合适.
2、“牛牛”饮料公司的一种瓶装饮料外包装上有“500±30(mL)”字样,请问“500±30(mL)”是什么含义?质检局对该产品抽查5瓶,容量分别为503mL,511mL,489mL,473mL,527mL ,问抽查产品的容量是否合格?
分析:500±30(mL)中,“500”指的是什么?“+30”是什么意思?“-30”是什么意思?
四、【展示质疑与小结】
五、【能力检测】
1、课本第4面练习.
2、一种零件的内径尺寸在图纸上是30±0.05(单位:毫米),表示这种零件的标准尺寸是30毫米,加工要求最大不超过标准尺寸___ ___毫米,最小不低于标准尺寸___ ___毫米.
3、21世纪第一年一些国家的服务出口额比上年的增长率如下:
美国 德国 英国 中国 日本 意大利
-3.4% -0.9% -5.3% 2.8% -7.3% 7.0%
这一年这六国中哪些国家的服务出口额增长了,哪些国家的服务出口额减少了?,哪国增长率最高,哪国增长率最低?
六、【课外拓展】
1、教科书5页习题4、5、:6、7题
2、10筐橘子,以每筐15㎏为标准,超过的千克数记作正数,不足的千克数记作负数。标重的记录情况如下:+1,-0.5,-0.5,-1,+0.5,-0.5,+0.5,+0.5,+0.5,-0.5。问这10筐橘子各重多少千克?总重多少千克?
3、一种零件的内径尺寸在图纸上是9±0.05(单位:mm),表示这种零件的标准尺寸是9mm,加工要求最大不超过标准尺寸多少 最小不小于标准尺寸多少
七、【星级评价】
自评☆☆☆ 他评 ☆☆☆ 师评☆☆☆ 及时订正△
1.2有理数核心知识框架图
1.2.1 有理数(第3课时)
主备人:刘玉环 审核人: 审核时间:
一、【目标导学】
核心知识 掌握有理数的概念,会对有理数按一定标准进行分类,
核心能力 了解分类的标准与分类结果的相关性,初步了解“集合”的含义;
情感态度 体验分类是数学上常用的处理问题方法。
【学习重点】:正确理解有理数的概念
【学习难点】:正确理解分类的标准和按照一定标准分类
二、【自主学习】
1、通过两节课的学习,,那么你能写出3个不同类的数吗 .(4名学生板书)
__________________________________________
2、P6练习(做在课本上)
三、【合作探究】
有理数的分类
小组中每人任意写出三个数,
问题1:观察这些数,我们将这些数做一下分类;该分为几类,又该怎样分呢?
分为 类,分别是:
引导归纳: 统称为整数, 统称为有理数。
问题2:我们是否可以把上述数分为两类 如果可以,应分为哪两类
归纳:所有的正数组成 集合,所有的负数组成 集合
问题3:把下列各数填入它所属于的集合的圈内:
15,-,-5,,,0.1,-5.32,-80,123,2.333.
正整数集合 负整数集合
正分数集合 负分数集合
四、【展示质疑与小结】
五、【能力检测】
1、下列各数,哪些是整数 哪些是分数 哪些是正数 哪些是负数
+7,-5, ,,79,0,0.67,,+5.1
2、把下列给数填在相应的大括号里:
-4,0.001,0,-1.7,15,.
正数集合{ …},负数集合{ …},
正整数集合{ …},分数集合{ …}
3、0是整数吗 自然数一定是整数吗 0一定是正整数吗 整数一定是自然数吗
六、【课外拓展】
图中两个圆圈分别表示正整数集合和整数集合,请写并填入两个圆圈的重叠部分.你能说出这个重叠部分表示什么数的集合吗
正数集合 整数集合
七、【星级评价】
自评☆☆☆ 他评 ☆☆☆ 师评☆☆☆ 及时订正△
1.2.2数轴(第4课时)
主备人:刘玉环 审核人: 审核时间:
一、【目标导学】
核心知识 掌握数轴概念,理解数轴上的点和有理数的对应关系;
核心能力 会正确地画出数轴,利用数轴上的点表示有理数;
情感态度 领会数形结合的重要思想方法。
【学习重难点】:数轴的概念和用数轴上的点表示有理数.
二、【自主学习】
看课本P7-9填空:
1、数轴的概念:
定义:规定了 、 和 的直线叫做数轴。
2、数轴的画法:
(1)画 、定原点,标出原点“O”.
(2)取原点向 方向为正方向,并标出箭头.
(3)选适当的长度作为单位长度,并标出…,-3,-2,-1,1,2, 3…各点,请同学们画一个数轴:
3、数轴定义的理解:
(1)规定了原点、正方向和单位长度的直线叫做 ,如图1所示.
(2)所有的有理数,都可以用数轴上的点表示.例如:
A点表示-4; B点表示 O点表示 D点表示
4、观察数轴可以知道:
(1)在数轴上表示的两数,右边的数总比左边的数 。
(2)由正、负数在数轴上的位置可知:正数都有大于 ,负数都小于 ,正数 一切负数。
三、【合作探究】
1、考考你:下列图形哪些是数轴?
2、 数轴上点A表示-3,
(1)在同一数轴上,点B表示-5,则A、B之间的距离是___,
(2) 在同一数轴上与点A相距5个单位的点表示的数是____
(3)点A到原点的距离是___
四、【展示质疑与小结】
1. 数轴有什么作用?2. 怎样画数轴?
五、【能力检测】
1、在数轴上,表示数-3,2.6,,0,,,-1的点中,在原点左边的点有 个。
2、在数轴上点A表示-4,如果把原点O向正方向移动1个单位,那么在新数轴上点A表示的数是( )
A.-5, B.-4 C.-3 D.-2
3、 (1)(请先在头脑中想象点的移动,尝试解决下面问题,然后再画图解答)一个点在数轴上表示的数是-5,这个点先向左边移动3个单位,然后再向右边移动6个单位,这时它表示的数是多少呢 如果按上面的移动规律,最后得到的点是2,则开始时它表示什么数
(2)你觉得数轴上的点表示数的大小与点的位置有关吗 为什么
六、【课外拓展】
教科书第15页习题5、6、7
七、【星级评价】
自评☆☆☆ 他评 ☆☆☆ 师评☆☆☆ 及时订正△
1.2.3 相反数(第5课时)
主备人:刘玉环 审核人: 审核时间:
一、【导学目标】
核心知识 借助数轴理解相反数的概念,会求一个数的相反数;
核心能力 养学生观察、猜想、归纳的能力,初步形成数形结合的思想。
情感态度 体验数学发展是生活实际的需要,激发学生学习数学的兴趣。
【学习重点】理解相反数的概念和求一个数的相反数
【学习难点】:相反数概念的理解。
二、【自主学习】
思考:1、数轴上与原点距离是2 的点有______个,这些点表示的数是_____
2、请两位同学背靠背,一个向左走5步,另一个向右走5步,如果向右走为正,向左、向右分别记作什么?
一般地,设a是一个正数,数轴上与原点的距离是a的点有___个,它们分别在原点的____,表示____和____,我们说这两点关于原点对称。
+3.6 和-3.6,6和-6 ,每对数,有什么相同和不同?
归纳:像+3.6和-3.6、6和-6、,只有____ 不同的两个数,叫互为相反数。其中一个叫另一个的相反数.
考考你:(1)-8的相反数是___, 7是____的相反数。
(2)a的相反数是_____.-a的相反数是____
(3) 怎样表示一个数的相反数?
归纳:在这个数的前面添上“-”,就可表示这个数的相反数。如12的相反数是____,-9的相反数是_____,如果在这个数的前面添上“+”表示____.
(4)互为相反数在轴上的位置有什么特点?
(5) 零的相反数是____.
三、【合作探究】
1 .判断下列说明是否正确
(1)-(-3)表示-3的相反数( ), (2)-2.5的相反数是2.5( )
(3)2.7与-3.7是互为相反数( ) (4)-π是相反数。( )
2 .分别写出下列各数的相反数:1.3 、-6
-0.2 、-(-3) 、π-1
3. 填空:(1) -(-0.8)=___, (2) –(-)=____,
(3) +(+4)=____, (4) –(-11)=_____
四、【展示质疑与小结】
五、【能力检测】
1、课本P10练习
2、填空:
①的相反数是 ; ② 的相反数是;
③若-x=10,则x的相反数在原点的 侧。
3、若 a 是负数,则 -a 是 ___数;若 -a 是负数,则 a 是______数.
六、【课外拓展】
1、化简下列各数中的符号:
(1) (2)-(+5)
(3) (4)
2、 填空:
(1)a-4的相反数是 ,3-x的相反数是 。
(2)是 的相反数。
(3)如果-a=-9,那么-a的相反数是 。
(4)若-(a-5)是负数,则a-5 0.
(5) 若是负数,则x+y 0.
3、 已知a、b在数轴上的位置如图所示。
在数轴上作出它们的相反数;
用“<”按从小到大的顺序将这两个数连接起来。
4、如果a-5与a互为相反数,求a.
七、【星级评价】
自评☆☆☆ 他评 ☆☆☆ 师评☆☆☆ 及时订正△
1.2.4绝对值(1)(第6课时)
主备人:刘玉环 审核人: 审核时间:
一、【目标导学】
核心知识 借助数轴,理解绝对值的概念,能求一个有理数的绝对值。
核心能力 会利用绝对值比较两个有理数的大小。
情感态度 经历将实际问题数学化的过程,感受数学与生活的关系,贯彻数形结合的思想。
【学习重点】:正确理解绝对值的概念,会求已知数的绝对值
【学习难点】:绝对值的几何意义,应用绝对值解决实际问题
二、【自主学习】
1、情境引入:两只小狗从同一点O出发,在一条笔直的街上跑,一只向右跑10米到达A点,另一只向左跑10米到达B点。
(1)若规定向右为正,则A处记做__________,B处记做__________;
(2)A处距离出发点“O” 米,B处距离出发点“O” 米;
(3)这两只小狗在跑的过程中,有没有共同的地方?
(4)在数轴上的A、B两点又有什么特征?
2、在数轴上找到-5和5的点,它们到原点的距离分别是多少?
3、绝对值的概念:在数轴上,一个数所对应的点与原点的距离叫做该数的 。用符号“ ”表示。例如:-5到原点的距离是 ,所以-5的绝对值是 ,记作:|-5|= ,5的绝对值是 ,记作 。
三、【合作探究】
如上图,学校位于数轴的原点处,小光、小明、小亮家分别位于点A、B、C处,单位长度表示1千米。小光家所在的位置对应的数是 ,与原点的距离是 ,那就是说,-2的绝对值是 ,记作= ;小明家所在的位置对应的数是 ,与原点的距离是 ,那就是说+1的绝对值是 1,记作 。
提问:互为相反数的两个数的绝对值有什么关系?
2、探索绝对值的性质:试一试,填空:
= ;= ;= ; = ;
提出问题:你能从上面的解答中发现什么规律吗?
总结:绝对值的性质:
(1)一个正数的绝对值等于 ;
(2)一个负数的绝对值等于它的 ;
(3)0的绝对值是 ;
(4)互为相反数的两个数的绝对值 。
四、【展示质疑与小结】
五、【能力检测】
1、课本P13习题第5、6、7题。
2、想一想:
(1)一个数的绝对值是它本身,这个数是什么数?
(2)一个数的绝对值是它的相反数,这个数是什么数?
【课外拓展】
1、用”>”、”<”、”=”连接下列两数:
∣∣___∣∣ ∣-3.5∣___-3.5
∣0∣____∣-0.58∣ ∣-5.9∣___∣-6.2∣
2、 数轴上与表示1的点的距离是2的点所表示的数有___________________.
3、 计算|4|+|0|-|-3|=______________.
4、绝对值的数学表示式:
七、【星级评价】
自评☆☆☆ 他评 ☆☆☆ 师评☆☆☆ 及时订正△
1.2.5有理数大小的比较(第7课时)
主备人:刘玉环 审核人: 审核时间:
一、【目标导学】
核心知识 借助数轴,理解有理数大小关系,会比较两个有理数的大小。
核心能力 能熟练运用法则结合数轴比较有理数的大小,特别是应用绝对值概念比较两个负数的大小,能利用数轴对多个有理数进行有序排列。
情感态度 转化思想[比较负数→比较正数
【学习重点】:会比较两个有理数的大小
【学习难点】:有理数大小比较法则中两个负数比较法则的理解
二、【自主学习】
问题一:3的绝对值是 ,-3的绝对值是 ;绝对值等于3的数是 ,0的绝对值是 ,
问题二:下面是某一天5个城市的最低气温:
哈尔滨-20℃、北京-10℃、长沙5℃、上海0℃、广州10℃
1、比较这一天下列两个城市间最低气温的高低(填“高于”或“低于”)
广州_______上海; 北京________哈尔滨;
武汉________哈尔滨; 武汉__________广州。
2、画一画:
(1)把上述5个城市最低气温的数表示在数轴上。
(2)观察这5个数在数轴上的位置,从中你发现了什么?
(3)温度的高低与相应的数在数轴上的位置有什么关系?
归纳: 在数轴上表示的两个数,右边的数总比左边的数 。
正数都大于 ,负数都小于 ,正数 负数。
三、【合作探究】
1、在数轴上表示数2,0,-3,-1,并比较它们的大小,将它们按从小到大的顺序用“<”号连接。
2、(1)求出数轴上各数的绝对值,并比较它们的大小.
(2)由上你发现了什么?
归纳: 两个正数比较大小,绝对值大的数 ;
两个负数比较大小,绝对值大的数反而 。
想一想:我们有几种方法来判断有理数的大小?你认为它们各有什么特点?
四、【展示质疑与小结】
五、【能力检测】
1、课本P13练习
2、课本P14-15习题第5,6、12题
3、(1) 整数x满足<3,则x=___________________,
(2)负整数x满足,则x=___________________
六、【课外拓展】
1.本节课主要学习了有理数大小比较的两种方法,一种是按照法则,两两比较,另一种是利用数轴,
2.绝对值比较时,分母相同,分子大的数 ;分子相同,则分母大的数反而 ;分子分母都不相同时,则应先通分再比较,或把分子化为相同再比较。
3.两个负数比较大小时的一般步骤:①求绝对值;②比较绝对值的大小;③比较负数的大小。
七、【星级评价】
自评☆☆☆ 他评 ☆☆☆ 师评☆☆☆ 及时订正△
1.3有理数的加、减法核心知识框架图
1.3.1有理数的加法(1)(第8课时)
主备人:刘玉环 审核人: 审核时间:
一、【目标导学】
核心知识 探索有理数加法法则,理解有理数的加法法则;
核心能力 能运用有理数加法法则,正确进行有理数加法运算;
情感态度 经历探索有理数加法法则的过程,体验数学来源于实践并为实践服务的思想,同时培养学生探究性学习的能力.
【学习重点】:有理数加法法则。
【学习难点】:异号两数相加的法则。
二、【自主学习】
1、比较大小:
(1)-π -3.14 (2)0.0001 -1000
看课本P19-20页填空:
1、有理数加法法则:
(1)、同号两数相加,取 的符号,并把 相加;
(2)、异号两数相加,取 符号,并用较 的绝对值减去较 的绝对值;
(3)、互为相反数的两个数相加得 ;
(4)、 一个数同0相加,仍得 。
三、【合作探究】
1、计算下列各式:
(1) (一8)+(一12); (2) (一3.75)+(-0.25);
(3)(一5)+9; (4)(-10)+7
(5)4+(-4) (6)(-9)+0
2、小慧原来在银行存有零用钱350元,上个月取出了120元,这个月计划再存人50元,请用有理数的加法计算:
(1)到上月底小慧在银行还有多少存款
(2)到这个月底小慧将有多少存款
四、【展示质疑与小结】
五、【能力检测】
1、课本P18练习
2、课本P24习题第1题
六、【课外拓展】
1.有理数的加法法则;
2.有理数加法的数轴表示;
3.有理数相加,先确定 ,再算绝对值;
4.有理数的加法运算,和不一定大于加数。
七、【星级评价】
自评☆☆☆ 他评 ☆☆☆ 师评☆☆☆ 及时订正△
1.3.1有理数的加法(二)(第9课时)
主备人:刘玉环 审核人: 审核时间:
一、【目标导学】
核心知识 进一步掌握有理数加法运算法则,理解加法运算律在有理数范围内推广的合理性;
核心能力 能运用加法运算律简化加法运算;
情感态度 经历有理数加法运算律的探索,体会观察、实践、归纳等活动在数学中的作用.
【学习重点】:运算律的理解及合理、灵活的运用。
【学习难点】:合理运用运算律。
二、【自主学习】
1、 计算下列各式:
(1)(+5)+(+8); (2)(-5)+(-8); (3)(+9)+(-2);
(4)(-9)+(+2); (5)(-9)+0; (6)0+0
2、计算下列各题:
(1) (-9.18)+6.18; (2) 6.18+(-9.18);
3、计算下列各题:
(1) [8+(-5)]+(-4); (2) 8+[(-5)+(-4)];
(3) [(-7)+(-10)]+(-11); (4) (-7)+[(-10)+(-11)];
(5) [(-22)+(-27)]+(+27); (6) (-22)+[(-27)+(+27)].
通过上面练习,观察得出:
交换律——两个有理数相加,交换加数的位置, 不变。
用代数式表示上面一段话:a+b=
结合律——三个数相加,先把前两个数相加,或者先把后两个数相加,和不变.用代数式表示上面一段话:(a+b)+c=
三、【合作探究】:
1、计算:(1) 33+(-2)+7+(-8) (2)4.375+(-82)+( -4.375)
小结:简化加法运算一般是三种方法:首先消去互为相反数的两数(其和为0),同号结合或凑整数。
四、【展示质疑与小结】
五、【能力检测】
1、课本P20练习:1、2
2、课本P24习题第2题
3、计算
(1) (2)(-9)+4+(-5)+8;
(3)(-36.35)+(-7.25)+26.35+(+7)
(4)
(5)
六、【课外拓展】
某出租车沿公路左右行驶,向左为正,向右为负,某天从A地出发后到收工回家所走的路线如下:(单位:千米)
⑴ 问收工时离出发点A多少千米?
⑵ 若该出租车每千米耗油0.3升,问从A地出发到收工共耗油多少升?
6.已知的相反数为-5,试求++(-)
7.计算:|1-|+|-|+|-|+…+|-|
七、【星级评价】
自评☆☆☆ 他评 ☆☆☆ 师评☆☆☆ 及时订正△
1.3.2有理数的减法(第10课时)
主备人:刘玉环 审核人: 审核时间:
一、【目标导学】
核心知识 理解有理数减法法则, 能熟练进行减法运算.
核心能力 会将减法转化为加法,进行加减混合运算,
情感态度 体会化归思想在数学中的作用.
【学习重点】:有理数减法法则和运算
【学习难点】:有理数减法法则的推导.
二、【自主学习】
1、填空:
(1)_______+6=20; (2)20+______=17;
(3)_______+(-2)=-20; (4)(-20)+____=-6?
2、学生独立看书,自学课本P.21~P.22
得出结论: 减去一个数等于加上这个数的_______ .
三、【合作探究】
1、 计算:
(1) 0-(-3.18) (2)(-10)-(-6) (3)-
2、某市元月中旬的平均气温是5℃,元月下旬因有寒流,预计气温将下降6~9℃,预计元月下旬的平均气温在什么范围内?
(理解、列式、计算)
总结反思:
(1) 有理数减法法则:减去一个数,等于加上这个数的 。
(2) 有理数减法的步骤:先变为 ,再改变 的符号,最后按有理数加法法则计算.
四、【展示质疑与小结】
五、【能力检测】
1.填空题:
(1)12-(+3)=___+___=___; (2)(-7)-(-6)=____+____=____;
(3)9-(-9)=____+____=___; (4)(-32)-(+13) ___+___=___.
2.计算:
(1)6-9; (2)(+4)-(-7); (3)(-5)-(-8);
(4) |-(-2.3)|-4.6; (5)1.9-(-0.6); (6)0-(-|5.4|)
3.计算
(1)比2℃低8℃的温度; (2)比-5℃低6℃的温度.
5.世界最高峰是珠穆朗玛峰,海拔高度是8848米,陆上最低处是位于亚洲西部的死海湖,湖面海拔高度是-392米,两处高度相差多少?
六、【课外拓展】
1.已知a = 8,b = -5,c = -3,求下列各式的值:
(1)a-b-c; (2)a-(c+b)
2.若a<0 , b>0, 则a, a+b, a-b, b中最大的是( )
A. a B. a+b C. a-b D. b
七、【星级评价】
自评☆☆☆ 他评 ☆☆☆ 师评☆☆☆ 及时订正△
1.3.2有理数的加、减法混合运算(第11课时)
主备人:刘玉环 审核人: 审核时间:
一、【目标导学】
核心知识 理解有理数减法法则, 能熟练进行减法运算.
核心能力 会将减法转化为加法,进行加减混合运算,
情感态度 体会化归思想在数学中的作用.
【学习重点】:有理数减法法则和运算
【学习难点】:有理数减法法则的推导.
二、【自主学习】
1、计算下列各式:
(1)(-18)-(-4); (2)(-18)-4; (3)(+18)-(-4)
2、请认真看课本第23页至24面的内容,要求解决两个问题:(1)有理数的加减混合运算与有理数的加法有什么联系?(2)有理数的加减混合运算有哪些步骤?
三、【合作探究】
(1)计算(-9)+(+6)-(-11)-7.(看到这个题目你想怎样做?你是怎么做的?)
若先把减法转化为加法,这时就成了___,___,___,___的和,正号通常可以省略,负号也可以通过化简省略,即
原式=________________________(省略正号并化简)
=_________________________(省略括号)
虽然加号、括号省略了,但-9+6+11-7仍表示-9,+6,+11,-7的和,所以这个算式可以读成什么?有哪两种读法?
(2)用加法运算律计算出结果
既然算式能看成几个数的和,我们可以运用加法的运算律进行计算,通常同号两数放在一起分别相加.
-9+6+11-7=(______)+(_______)
那么:-9+6+11-7接下来该怎样计算?
-9+6+11-7=________________=_______________=______
展示交流:全班合作交流,教师点拨后得出有理数加减混合运算的一般步骤:
(1)__________;(2)__________;(3)_________;(4)________;(5) __________
巩固练习:计算 (1)-4+7-4 (2)+6+9-15+31、
四、【展示质疑与小结】
1、 有理数减法法则:减去一个数,等于加上这个数的 。
2、 有理数减法的步骤:先变为 ,再改变 的符号,最后按有理数加法法则计算。
五、【能力检测】
1.填空题:
1.-4+7-4=-_____ - ______ + ________
2.+6+9-15+3=______________________
3.-9-3+2-4=_______9_______3_____4_____2
4.____________
2. 计算
(1)(+9)-(+10)+(-2)-(-8)+3; (2)
3.计算
(1)(+9)-(+10)+(-2)-(-8)+3 (2)
六、【课外拓展】
计算:(1)一天早晨的气温是-7℃,中午上升了11℃,半夜又下降了9℃,半夜的温度是多少?
(2)有8筐白菜,以每筐25千克为准,超过的千克数记作正数,不足的千克数记作负数,称后的记录如下:
1.5, -3.2, -0.5, 1, -2, -2, -2.5。 则这筐白菜一共多少千克?
七、【星级评价】
自评☆☆☆ 他评 ☆☆☆ 师评☆☆☆ 及时订正△
1.4有理数的乘、除法核心知识框架图
1.4.1有理数的乘法(1)(第12课时)
主备人:刘玉环 审核人: 审核时间:
一、【目标导学】
核心知识 掌握有理数乘法法则,初步了解有理数乘法法则的合理性。
核心能力 能够运用法则进行简单的有理数的乘法运算。
情感态度 通过对问题的变式探索,培养观察、归纳、猜测、验证能力。
【学习重点】:能按有理数乘法法则进行简单的有理数乘法运算。
【学习难点】:有理数乘法法则的推导。
1.了解有理数乘法的实际意义,理解有理数的乘法法则;
2. 能熟练地进行有理数的乘法运算.
二、【自主学习】
1.有理数加法法则内容是什么?
2.计算:
(1)2+2+2= (2)(-2)+(-2)+(-2)=
3.你能将上面两个算式写成乘法算式吗?
三、【合作探究】
1.自学课本28-29页回答下列问题
(1)如果它以每分2cm的速度向右爬行,3分钟后它在什么位置
可以表示为 .
(2)如果它以每分2cm的速度向左爬行,3分钟后它在什么位置
可以表示为
(3) 如果它以每分2cm的速度向右爬行,3分钟前它在什么位置
可以表示为
(4)如果它以每分2cm的速度向左爬行,3分钟前它在什么位置
可以表示为
由上可知:(1) 2×3 = ; (2)(-2)×3 = ;
(3)(+2)×(-3)= ; (4)(-2)×(-3)= ;
(5)两个数相乘,一个数是0时,结果为0
观察上面的式子, 你有什么发现?能说出有理数乘法法则吗?
归纳有理数乘法法则:
两数相乘,同号 ,异号 ,并把 相乘。
任何数与0相乘,都得 。
四、【展示质疑与小结】
五、【能力检测】
1.计算:
(1)0.25×(-4) (2)0×(-0.125) (3) (-)×(-0.5)
(4) (-)×6 (5)(-)×(-0.125) (6)(- 0.25) ×
2.对于有理数a、b定义一种运算:a*b=2a-b,计算(-2)*3+1
六、【课外拓展】
初一年级共100名学生,在一次数学测试中以90分为标准,超过的记为正,不足的记为负,成绩如下:
人数 10 20 5 14 12 18 10 4 9 6 2
成绩 -1 +3 -2 +1 +10 +2 0 -7 +7 -9 -12
请你算出这次考试的平均成绩.
七、【星级评价】
自评☆☆☆ 他评 ☆☆☆ 师评☆☆☆ 及时订正△
1.4.1有理数的乘法(2)(第13课时)
主备人:刘玉环 审核人: 审核时间:
一、【目标导学】
核心知识 经历探索多个有理数相乘的符号确定法则;
核心能力 会进行有理数的乘法运算;
情感态度 通过对问题的探索,培养观察、分析和概括的能力。
【学习重点】:多个有理数乘法运算符号的确定;
【学习难点】:正确进行多个有理数的乘法运算。
二、【自主学习】
1、有理数乘法法则:
2、计算:(1)(-0.75)×(-2)= (2)(-0.125)×8=
三、【合作探究】
观察:下列各式的积是正的还是负的?
2×3×4×(-5),
2×3×(-4)×(-5),
2×(-3)× (-4)×(-5),
(-2) ×(-3) ×(-4) ×(-5);
思考:几个不是0的数相乘,积的符号与负因数的个数之间有什么关系?
分组讨论交流,再用自己的语言表达所发现的规律:
几个不是0的数相乘,负因数的个数是 时,积是正数;负因数的个数是 时,积是负数。
例题:(1)
(2)
请你思考,多个不是0的数相乘,先做哪一步,再做哪一步?
你能看出下列式子的结果吗?如果能,理由
7.8×(-8.1)×O× (-19.6)
四、【展示质疑与小结】
五、【能力检测】
1、选择:(1).若干个不等于0的有理数相乘,积的符号( )
A.由因数的个数决定 B.由正因数的个数决定
C.由负因数的个数决定 D.由负因数和正因数个数的差为决定
2、下列运算结果为负值的是( )
A.(-7)×(-6) B.(-6)+(-4) C. 0×(-2)(-3) D.(-7)-(-15)
3、下列运算错误的是( )
A.(-2)×(-3)=6 B.
C.(-5)×(-2)×(-4)=-40 D.(-3)×(-2)×(-4)=-24
二、计算:
(1)、—5×8×(—7)×(—0.25);
(2);
六、【课外拓展】
(1)、 ;
(2)、 ;
七、【星级评价】
自评☆☆☆ 他评 ☆☆☆ 师评☆☆☆ 及时订正△
1.4.1有理数的乘法(3)(第14课时)
主备人:刘玉环 审核人: 审核时间:
一、【目标导学】
核心知识 通过自己动手实际操作,证明有理数运算中乘法的交换律、结合律以及分配律依然成立;
核心能力 通过对问题的探索,培养观察、分析和概括的能力。
情感态度 培养积极参与对数学问题的讨论的能力,敢于发表自己的观点,并用实例来给予证明,培养对数学的好奇心
【学习重点】:理解有理数乘法依然满足交换律、结合律与分配律,并会利用它们进行简化运算。
【学习难点】:运用乘法的交换律、结合律、分配律进行简化运算的原则。
二、【自主学习】
1、计算
(1)(-78)×5= (2)(-8)×(-2.5)=
2、做一做,并比较它们的结果。
(-2) ×7= , 7×(-2)=
(-3)×(-4)= ,(-4)×(-3)=
由上面的两组式子,我们发现乘法满足
[3×(-4)]×(-5)= ×(-5)=
3×[(-4)×(-5)]=3× =
由上面的两组式子,我们发现乘法满足
(-6)×[4+(-9)]=(-6)× =
(-6)×4+(-6)×(-9)= + =
由上面的两组式子,我们发现乘法满足
请用字母表示乘法的交换律、结合律与分配律:
乘法的交换律:
乘法的结合律:
乘法的分配律:
三、【合作探究】
1、计算:(1) (2)
2、某校体育器材室共有60个篮球。一天课外活动,有3个级分别计划借篮球总数的,和。请你算一算,这60个篮球够借吗?如果够了,还多几个篮球?如果不够,还缺几个?
四、【展示质疑与小结】
五、【能力检测】
1.运用运算律填空.
(1)-2×=×(_____).
(2)[×2]×(-4)=×[(______)×(______)].
(3)×[+]=×(_____)+(_____)×
2.选择题:利用分配律计算时,正确的方案是 ( )
A B
C D
3.运用运算律计算:
(1)(-25)×(-85)×(-4) (2) eq \b(--)×16
(3)60×-60×+60× (4)(—100)×(-+-0.1)
六、【课外拓展】
1. 已知:互为相反数,c、d互为倒数,x的绝对值是1,求:
3x—[(a+b)+cd]x的值
2. 定义一种运算符号△的意义:a△b=ab—1,求:
2△(—3)、2△[(—3)—5]的值
七、【星级评价】
自评☆☆☆ 他评 ☆☆☆ 师评☆☆☆ 及时订正△
1.4.2有理数的除法(第15课时)
主备人:刘玉环 审核人: 审核时间:
一、【目标导学】
核心知识 了解有理数除法的定义;理解倒数概念,会求有理数的倒数;
核心能力 掌握除法法则,会进行有理数的除法运算;
情感态度 培养积极参与对数学问题的讨论的能力,敢于发表自己的观点,并用实例来给予证明,培养对数学的好奇心
【学习重点】:正确进行有理数除法的运算,正确求一个有理数的倒数
【学习难点】:如何进行有理数除法的运算,求一个负数的倒数。
二、【自主学习】
1、 (-2) × 8 = 7×(-3)=
(-3)×(-5)= (-4)×(-3)=
×( )=1; 0.5×( )=1;
-4×( )=1; ×( )=1.
2、(1)6个同样大小的苹果平均分给3个小孩,每个小孩分到几个苹果?
(2)怎样计算下列各式? (独立思考后,再将结果与同桌交流)
(-6)÷3 6÷(-3) (-6)÷(-3) 0÷4
归纳:同号两数相除得( ),异号两数相除得( )并且把它们的( )相除0除以以何一个不为等于0的数都得( )
2、比较下列各组数的计算结果
(1) 1÷5 与1× (2)2÷() 与 2×
归纳:如果两个数的乘积等于1,那么把其中一个数叫做另一个数的( ),也称这两个数( )。除以一个非零数等于乘上这个数的( )
三、【合作探究】
1、(1)(-18)÷6= (2)(-63)÷(-7)=
(3)0÷(-8)= (4)16÷(-3)=
2、-6的倒数是________ -6 的倒数的倒数是________
-6 的相反数是________ -6 的相反数的相反数是________
四、【展示质疑与小结】
五、【能力检测】
1、(1)()÷()= ( 2)(-6.5)÷0.13 =
(3)()÷()= (4)÷(-1)=
(5)的倒数是 (6) 的相反数是
3、1.4的倒数是 ; 若a,b互为倒数,则2ab= ;
4、若一个数和它的倒数相等,则这个数是 ;若一个数和它的相反数相等,则这个数是 ;
六、【课外拓展】
1.果两个有理数的和除以它们的积,所得的商是0,那么这两个有理数 ( )
A.互为相反数,但不等于0 ; B.互为倒数 ; C.有一个等于0 ; D.都等于0
2.b≠0,则+的取值不可能是 ( )
A.0 B.1 C.2 D.-2
3.++=1,求()2003÷(××)的值。
七、【星级评价】
自评☆☆☆ 他评 ☆☆☆ 师评☆☆☆ 及时订正△
1.4.2有理数的运算顺序(第16课时)
主备人:刘玉环 审核人: 审核时间:
一、【目标导学】
核心知识 掌握有理数加、减、乘、除运算顺序
核心能力 会正确合理地进行有理数运算;
情感态度 培养学生严谨的学习习惯。
【学习重点】:正确进行有理数的混合运算。
【学习难点】:正确合理地进行运算。
二、【自主学习】
一、自主学习
1、计算
(1) (-8)÷(-4); (2) (-9)÷3 (3) (—0.1)÷×(—100);
2. 有理数的除法法则
3、 计算
(1)(—8)+4÷(-2) (2)(-7)×(-5)—90÷(-15)
你的计算方法是先算 法,再算 法。
有理数加减乘除的混合运算顺序应该是 写出解答过程
2.自学完成例9(阅读课本P36—P37页内容)
三、【合作探究】
1、计算(P36练习)
(1)6—(—12)÷(—3);(2)(—48)÷8—(—25)×(—6);
( 3);
四、【展示质疑与小结】
五、【能力检测】
1、选择题
(1)下列运算有错误的是( )
A.÷(-3)=3×(-3) B.
C.8-(-2)=8+2 D.2-7=(+2)+(-7)
(2)下列运算正确的是( )
A. ; B.0-2=-2; C. D.(-2)÷(-4)=2;
2、计算
1)、18—6÷(—2)× ; 2)11+(—22)—3×(—11);
六【课外拓展】
(1) (-)÷(-)÷(-) (2)
(3) (4)
七、【星级评价】
自评☆☆☆ 他评 ☆☆☆ 师评☆☆☆ 及时订正△
1.5有理数的乘方核心知识框架图
1.5.1有理数的乘方(第17课时)
主备人:刘玉环 审核人: 审核时间:
一、【目标导学】
核心知识 理解乘方的意义,探究有理数乘方的符号法则;
核心能力 会正确进行有理数乘方运算。
情感态度 经历探索有理数乘方的运算,获得解决问题经验。
【学习重点】:有理数乘方的意义以及有理数乘方的运算
【学习难点】:有理数乘方运算以及符号法则
二、【自主学习】
1、复习巩固:
①乘法运算的符号法则及运算方法:
②多个不为0的数相乘,积的符号怎样确定?
2、导学:
(1)一般地,几个相同因数相乘,即,记作 ,读作
求n个相同因数的 ,叫作乘方,乘方的结果叫做 。 在中,叫做 ,叫作 。当看作的次方的结果时,也可读作 。
特别地一个数也可以看作这数本身的一次方,如5就是5的一次,即,指数为1通常 不写。
(2)警示:
①乘方是一种运算(乘法运算的特例),即求个相同因数连乘的简便形式;
②幂是乘方的结果,它不能单独存在,即没有乘方就无所谓幂;
③乘方具有双重含义:既表示一种 ,又表示乘方运算的结果;
④书写格式:若底数是负数、分数或含运算关系的式子时,必须要用 把底数括起来,以体现底数的整体性。
(3)拓展:底数为,0,1,10,0.1的幂的特性:
(n为正整数) (n为整数)
(1后面有____个0), =0.00…01 (1前面有______个0)
(4)乘方的符号法则:
负数的奇次幂是 数,负数的偶次幂是 数。
正数的任何次幂都是 数,0的任何正整数次幂都是 。
三、【合作探究】
1、计算:
, , , ,
, ,
2、 ;
3、已知n是正整数,那么 , 4、如果一个有理数的偶次幂是非负数,那么这个有理数是 。
A、正数 B、负数 C、0 D、任何有理数
5、平方等于9的数是 ,立方等于27的数是 ,平方等于本身的数是 ,立方等于本身的数是
四、【展示质疑与小结】
五、【能力检测】
1、把写成乘方形式 。
2、计算: , ,
3、若,则 若,则
六、【课外拓展】
1、计算:
2、观察下列数,根据规律写出横线上的数
;;;;______;第2010个数是____________。
七、【星级评价】
自评☆☆☆ 他评 ☆☆☆ 师评☆☆☆ 及时订正△
1.5.1有理数的乘方(第18课时)
主备人:刘玉环 审核人: 审核时间:
一、【目标导学】
核心知识 能确定有理数加、减、乘、除、乘方混合运算的顺序;
核心能力 及时纠正运算中的错误,进一步培养学生正确迅速的运算能力。
情感态度 培养学生严谨的学习态度。
【学习重点】:有理数的混合运算;
【学习难点】:运算顺序的确定和性质符号的处理。
二、【自主学习】
(一)复习回顾:
1、有理数的加、减、乘、除及乘方的运算法则
2、加入乘方后,有理数的混合运算的顺序如何?
(二)导学:
有理数的混合运算顺序:(1)先 ,再 ,最后 ;(2)同级运算,从左到右进行;(3)如有括号,先做 的运算,按小括号、中括号、大括号依次进行。
方法规律:
(1)有理数运算分三级运算,加减法是第一级运算,乘除法是第二级运算,乘方和开方(以后学习)是第 级运算。
运算顺序是:先算高级运算,再算 运算;同级运算,再按从左至右的顺序运算。
(2)在运算过程中注意运算律的运用
(三)完成P43例3及P44的练习
三、【合作探究】
1、计算:
(1)
(2)
(3)
2、观察下面行数:
① -3,9,-27,81,-243,729,…
② 0,12,-24,84,-240,732,…
③ -1,3,-9,27,-81,243,…
(1)第①行数有什么规律?
(2)第②行数与第①行数有什么关系?
(3)第③行数与第①行数有什么关系?
(3)取每行数的第10个数,计算这三个数的和
四、【展示质疑与小结】
五、【能力检测】
1、计算:
2、、为有理数,且,求的值;
4、一根1米长的绳子,第一次剪去,第二次剪去剩下的,如此剪下去,第六次后剩下的绳子还有1厘米长吗?为什么?
六、【课外拓展】
已知
试求的值
七、【星级评价】
自评☆☆☆ 他评 ☆☆☆ 师评☆☆☆ 及时订正△
1.5.2科学计数法(第19课时)
主备人:刘玉环 审核人: 审核时间:
一、【目标导学】
核心知识 了解科学记数法的意义,弄清科学记数法中10的指数n与这个数的整数位数的关系。
核心能力 会用科学记数表示绝对值大于10的数;
情感态度 体会科学记数法的优点。
【学习重点】:用科学记数法表示绝对值大于10的数;
【学习难点】:正确使用科学记数法表示数
二、【自主学习】
1、展示你收集的你认为非常大的数,与同学交流,你觉得记录这些数据方便吗?
2、现实生活中,我们会遇到一些比较大的数,如太阳的半径、光速,日前世界人口等,读写这样大的数有一定的困难,先看10的乘方的特点:
1000 000 1000 000 000
10…..0(在1后面有 个0)
对于一般的大数如何简单地表示出来?
3000 000 000 1000 000 000
696000 100 000
读作6.96乘10的5次方(幂)
3、科学记数法:
像上面这样,把一个大于10的数表示成 的形式(其中是整数数位只有一位的数,n是整数),使用的是科学记数法,“科学记数”谨记三点:
(1)弄清a×中的a的取值范围
(2)正确确定a×中的n的值,当所记数大于10时,n是 且等于所记数的整数位数 。
(3)会将用科学记数法表示的数还原。
提醒:a符号与原数的符号相同,如:将科学记数时,a为而不是。
三、【合作探究】
1、用科学记数法表示下列各数:
1000 000; 572 000 000; 123 000 000 000;
; ;
2、第五次人口普查知山西省人口总数约为3297万人,用科学记数法表示是多少人?
3、太阳直径为千米,其原数为多少米?
四、【展示质疑与小结】
五、【能力检测】
1、用科学记数法表示下列各数
10000; 800000; 567000; 000;
2、下列用科学记数法写出的数,原数分别是什么数?
4.5 7.04 3.96
3、下列各数,属于科学记数法表示的是 。
A、53.7 B、0.537 C、537 D、5.37
4、在比例尺为1:8000 000的地图上,量得太原到北京的距离为6.4㎝,将实际距离用科学记数法表示为 ㎞。
六、【课外拓展】
地球绕太阳公转的速度约为1.1㎞/h,声音在空气中传播速度为330m/s,试比较这两个速度的大小。
七、【星级评价】
自评☆☆☆ 他评 ☆☆☆ 师评☆☆☆ 及时订正△
1.5.3近似数(第20课时)
主备人:刘玉环 审核人: 审核时间:
一、【目标导学】
核心知识 了解近似数和有效数字的概念,
核心能力 能按要求取近似数和保留有效数字;
情感态度 体会近似数的意义及在生活中的应用。
【学习重点】:能按要求取近似数和有效数字;
【学习难点】:有效数字概念的理解。
二、【自主学习】
1.用科学记数法表示下列各数:
(1)1250000000= ;(2)-130000= ;
(3)-1025000= ;
2.下列用科学记数法表示的数,把原数写在横线上:
(1) ;(2)
三、【合作探究】
1.(1)我们班有 名学生, 名男生, 名女生;
(2)一天有 小时,一小时有 分,一分钟有 秒;
(3)我的体重约为 千克,我的身高约为 厘米;
(4)我国大约有 亿人口.
在上题中,第 题中的数字是准确的,第 题中的数字是与实际接近的。这种只是接近实际数字,但与实际数字还有差别的数被称为近似数。
2.你还能举出生活中的准确数与近似数吗?请将你举的例子写在下面的空白处。
3.近似数与准确数的接近程度,可以用精确度表示(就是按四舍五入保留小数)。
按四舍五入对圆周率取近似数时,有:
(精确到个位),
(精确到 0.1 ,或叫精确到十分位),
(精确到 ,或叫精确到 位),
(精确到 ,或叫精确到 位),
(精确到 ,或叫精确到 位)。……
4.例6按括号内的要求,用四舍五入法对下列各数取近似数:
(1)0.0158(精确到0.001); (2)304.35(精确到个位);
(3)1.804(精确到0.1); (4)1.804(精确到0.01);
解:(1) (2)
(3) (4)
思考:1.8,与1.80的精确度相同吗?在表示近似数时,能将小数点后的0随便去掉吗?
归纳:从一个数的左边________________, 到_______________止,所有的数字都是这个数的有效数字。
四、【展示质疑与小结】
五、【能力检测】
P46练习
用四舍五入法对它们取近似数,并写出各近似数数的有效数字
(1)0.00356(精确到万分位); (2)61.235(精确到个位);
(3)1.8935(精确到0.001); (4)0.0571(精确到0.1);
六、【课外拓展】
P47 T 6、9、10
七、【星级评价】
自评☆☆☆ 他评 ☆☆☆ 师评☆☆☆ 及时订正△
单元小结(第21课时)
主备人:刘玉环 审核人: 审核时间:
一、【目标导学】
核心知识 、复习整理有理数有关概念和有理数运算法则,运算律以及近似计算等有关知识;
核心能力 培养学生综合运用知识解决问题的能力;
情感态度 渗透数形结合的思想。
【学习重点】:有理数概念和有理数运算;
【学习难点】:负数和有理数法则的理解。
二、【自主学习】
2、知识专题部分:
专题1加法的运算律例1:计算:
专题2乘法的运算律及分配律
例2:计算:
专题3 充分利用概念
例3:已知a.b互为相反数,c.d互为倒数,m是绝对值最小的数,求代数式的值。
专题4 非负数性质的应用
例4:已知,求的值。
专题5 数形结合的思想方法
例5:有理数a.b在数轴上的位置如图所示 ,试比较:,,,这四个数的大小
专题6 公式的递用解题法
例6:计算: ①; ②
专题7 分类讨论的思想方法
例7:已知a是任一有理数,试比较与的大小.
专题8 特殊值法
例8:若,,且,则 0(填“”或“”)
三、【合作探究】
1、计算:
(1) (2)、
2、若m、n互为相反数,x、y互为倒数,求的值。
3、若与互为相反数,求的值。
4、已知有理数a、b、c在数轴上的位置,如图所示,化简.
四、【展示质疑与小结】
全章复习的目的是使学生进一步系统掌握基础知识、基本技能和基本方法,进一步提高综合运用数学知识灵活地分析和解决问题的能力?因此,我们应注意下面两个方面:第一,既加强基础,又提高能力和发展智力;第二,既全面复习,又突出重点?。
五、【能力检测】
1、写出下列各数的相反数和倒数?
原 数 5 -6 1 0?5 -1
相反数
倒 数
2、?计算:
(1); (2)(-81)÷÷(-16);
(3)22+(-2)3×5-(-0.28)÷(-2)2 (4)[(-3)3-(-5)3]÷[(-3)-(-5)]?
六、【课外拓展】
1、计算:
2、计算:
3、试比较与的大小。
七、【星级评价】
评☆☆☆ 他评 ☆☆☆ 师评☆☆☆ 及时订正△
青,取之于蓝,而青于蓝
正数和负数的概念
一组相反意义的量
正数和负数
正数和负数的应用
冰,水为之,而寒于水
助教策略
(学习随笔)
引导学生思考讨论,借助举例说明。
阅读思考。
方法指导:先独立完成,然后组内小展示时组长帮助组员学会。
1、本节课你有那些收获?
2、还有没解决的问题吗?
木直中绳,輮以为轮,其曲中规,虽有槁暴,不复挺者,輮使之然也
助教策略
(学习随笔)
方法指导:独立完成后,小组内的对子间互相用红笔互改,有疑问的由组长组织讨论订正。
故木受绳则直,金就砺则利,君子博学而日参省乎己,则知明而行无过矣
助教策略
(学习随笔)
通过上节课的学习,我们知道在实际生产和生活中存在着两种不同意义的量,为了区分它们,我们用正数和负数来分别表示它们.
通过问题3提醒学生审题时要注意要求,题中求的是增长率,不是增长值.
1、本节课你有那些收获?
2、还有没解决的问题吗?
吾尝跂而望矣,不如登高之博见也
教策略
(学习随笔)
方法指导:独立完成后,小组内的对子间互相用红笔互改,有疑问的由组长组织讨论订正。)
不临深溪,不知地之厚也
按整数、分数分:
按正数、负数、零分:
有理数的分类
意义:
在数轴上表示:
相反数
有理数
在数轴上:
利用绝对值:
有理数的大小比较方法
几何意义:
代数意义:
绝对值:
倒数意义:
行衢道者不至,事两君者不容。
助教策略
(学习随笔)
问题3中,首先要解释集合的含义.练习2中可补充思考:四个集合合并在一起是什么集合 (若降低难度可分开问)
不闻先王之遗言,不知学问之大也
助教策略
(学习随笔)
此题是一个探索题,有一定难度,可以分步完成,不如先写出正数,在写出整数,观察都具备的是其中哪个数.
蓬生麻中,不扶而直;
助教策略
(学习随笔)
学生观察,思考,研究,表示.增强学生的合作意识.
满足的条件可以先不必明确,基本能明确就可以,在后面逐步明
明确数轴的正确画法和要求.
练习中注意纠正学生数轴画法的错误和点的表示错误
白沙在涅,与之俱黑
助教策略
(学习随笔)
总结可以由教师提出问题,学生总结,教师完善
2题也可以启发学生反过来想,即点A向正方向移动1个单位.
3题有一定的难度,两次变动可转化成原点实际怎样移动了,移动了几个单位,那么-5实际上怎样移动了
干、越、夷、貉之子,生而同声,长而异俗,教使之然也
助教策略
(学习随笔)
知识回顾,导入新课。
观察、 归纳,提升学生发现问题的能力
物类之起,必有所始。
助教策略
(学习随笔)
神莫大于化道,福莫长于无祸
小节:相反数的概念及注意事项
助教策略
(学习随笔)
登高而招,臂非加长也,而见者远
助教策略
(学习随笔)
以开放的形式创设情境,以学生进行讨论,并培养分类的能力,培养学生的观察与归纳能力,渗透数形思想
方法指导:先独立完成,然后组内小展示时组长帮助组员学会。
登高而招,臂非加长也,而见者远
助教策略
(学习随笔)
方法指导:独立完成后,小组内的对子间互相用红笔互改,有疑问的由组长组织讨论订正。
顺风而呼,声非加疾也,而闻者彰
助教策略
(学习随笔)
方法指导:独立完成自主学习
方法指导:先独立完成,然后组内小展示时组长帮助组员学会。
假舆马者,非利足也,而致千里
0
1
-1
-2
2
0
1
-1
-2
2
助教策略
(学习随笔)
0
1
-1
-2
2
本节课我们学习了哪些内容?
方法指导:独立完成后,小组内的对子间互相用红笔互改,有疑问的由组长组织讨论订正。
假舟楫者,非能水也,而绝江河
有理数的加
、
减运算
法则
加法法则
减法法则
有理数加、减混合运算法则
运算律
加法交换律
字母表示:
文字叙述:
加法结合律
字母表示:
文字叙述:
简便计算
声无小而不闻,行无隐而不形 。
助教策略
(学习随笔)
方法指导:独立完成自主学习
方法指导:先独立完成,然后组内小展示时组长帮助组员学会。
君子生非异也,善假于物也
助教策略
(学习随笔)
本节课我们学习了哪些内容?
方法指导:独立完成后,小组内的对子间互相用红笔互改,有疑问的由组长组织讨论订正。
物类之起,必有所始
助教策略
(学习随笔)
方法指导:独立完成自主学习
荣辱之来,必象其德
助教策略
(学习随笔)
方法指导:先独立完成,然后组内小展示时组长帮助组员学会。
本节课我们学习了哪些内容?
方法指导:独立完成后,小组内的对子间互相用红笔互改,有疑问的由组长组织讨论订正。
肉腐出虫,鱼枯生蠹
助教策略
(学习随笔)
荣辱之来,必象其德
助教策略
(学习随笔)
方法指导:独立完成自主学习
方法指导:先独立完成,然后组内小展示时组长帮助组员学会。
怠慢忘身,祸灾乃作
助教策略
(学习随笔)
本节课我们学习了哪些内容?
方法指导:独立完成后,小组内的对子间互相用红笔互改,有疑问的由组长组织讨论订正。
强自取柱,柔自取束。
助教策略
(学习随笔)
方法指导:独立完成自主学习
方法指导:先独立完成,然后组内小展示时组长帮助组员学会。
白沙在涅,与之俱黑
助教策略
(学习随笔)
本节课我们学习了哪些内容?
方法指导:独立完成后,小组内的对子间互相用红笔互改,有疑问的由组长组织讨论订正。
草木畴生,禽兽群焉,物各从其类也。
乘法法则
除法法则
有理数乘、除混合运算法则
法则
有理数的乘
、
除运算
字母表示:
文字叙述:
乘法交换律
简便计算
运算律
字母表示:
文字叙述:
乘法结合律
字母表示:
文字叙述:
乘法分配律
玉在山而草润,渊生珠而崖不枯。
助教策略
(学习随笔)
方法指导:独立完成自主学习
方法指导:先独立完成,然后组内小展示时组长帮助组员学会。
是故质的张,而弓矢至焉;林木茂,而斧斤至焉
助教策略
(学习随笔)
本节课我们学习了哪些内容?
方法指导:独立完成后,小组内的对子间互相用红笔互改,有疑问的由组长组织讨论订正。
邪秽在身,怨之所构
助教策略
(学习随笔)
方法指导:独立完成自主学习
方法指导:先独立完成,然后组内小展示时组长帮助组员学会。
施薪若一,火就燥也,平地若一,水就湿也
助教策略
(学习随笔)
本节课我们学习了哪些内容?
方法指导:独立完成后,小组内的对子间互相用红笔互改,有疑问的由组长组织讨论订正。
积土成山,风雨兴焉
助教策略
(学习随笔)
方法指导:独立完成自主学习
方法指导:先独立完成,然后组内小展示时组长帮助组员学会。
积水成渊,蛟龙生焉
助教策略
(学习随笔)
本节课我们学习了哪些内容?
方法指导:独立完成后,小组内的对子间互相用红笔互改,有疑问的由组长组织讨论订正。
积善成德,而神明自得,圣心备焉
助教策略
(学习随笔)
方法指导:独立完成自主学习
方法指导:先独立完成,然后组内小展示时组长帮助组员学会。
故不积跬步,无以至千里
助教策略
(学习随笔)
本节课我们学习了哪些内容?
方法指导:独立完成后,小组内的对子间互相用红笔互改,有疑问的由组长组织讨论订正。
不积小流,无以成江海
助教策略
(学习随笔)
方法指导:独立完成自主学习
方法指导:先独立完成,然后组内小展示时组长帮助组员学会。
本节课我们学习了哪些内容?
其数则始乎诵经,终乎读礼
助教策略
(学习随笔)
方法指导:独立完成后,小组内的对子间互相用红笔互改,有疑问的由组长组织讨论订正。
骐骥一跃,不能十步
有理数的乘方运算法则
运算顺序
运算律的应用
有理数的乘方运算
有理数混合运算法则
科学记数法:a
近似数与有效数字的意义
玉在山而草润,渊生珠而崖不枯。
助教策略
(学习随笔)
方法指导:独立完成自主学习
n为奇数
n为偶数
锲而舍之,朽木不折
助教策略
(学习随笔)
方法指导:先独立完成,然后组内小展示时组长帮助组员学会。
本节课我们学习了哪些内容?
方法指导:独立完成后,小组内的对子间互相用红笔互改,有疑问的由组长组织讨论订正。
邪秽在身,怨之所构。
助教策略
(学习随笔)
方法指导:独立完成自主学习
方法指导:先独立完成,然后组内小展示时组长帮助组员学会。
伯牙鼓琴,而六马仰秣
助教策略
(学习随笔)
本节课我们学习了哪些内容?
方法指导:独立完成后,小组内的对子间互相用红笔互改,有疑问的由组长组织讨论订正。
故声无小而不闻,行无隐而不形
助教策略
(学习随笔)
方法指导:独立完成自主学习
方法指导:先独立完成,然后组内小展示时组长帮助组员学会。
玉在山而草润,渊生珠而崖不枯
助教策略
(学习随笔)
本节课我们学习了哪些内容?
方法指导:独立完成后,小组内的对子间互相用红笔互改,有疑问的由组长组织讨论订正。
为善不积邪?安有不闻者乎
助教策略
(学习随笔)
方法指导:独立完成自主学习
方法指导:先独立完成,然后组内小展示时组长帮助组员学会。
故学数有终,若其义则不可须臾舍也
本节课我们学习了哪些内容?
方法指导:独立完成后,小组内的对子间互相用红笔互改,有疑问的由组长组织讨论订正。
为之,人也;舍 之,禽兽也
助教策略
(学习随笔)
鼓励学生独立思考回答以上问题。组织学生讨论交流,梳理本章内容。
有理数
有理数的分类
按整数、分数分:
按正数、负数、零分:
意义:
在数轴上表示:
相反数
倒数意义:
有理数的大小比较方法
运算
在数轴上:
利用绝对值:
绝对值:
1、几何意义:
2、代数意义:
概念
法则
加法法则
减法法则
乘法法则
除法法则
乘方法则
有理数混合运算法则
运算律
交换律
1、加法交换律
2、乘法交换律
字母表示:
文字叙述:
字母表示:
文字叙述:
结合律
1、加法结合律
2、乘法结合律
字母表示:
文字叙述:
字母表示:
文字叙述:
分配律
字母表示:
文字叙述:
3、科学记数法的意义:
4、近似数与有效数字的意义:
驽马十驾,功在不舍
先组织学生独立尝试,再小组展示质疑。
. . .
a o b
为善不积邪?安有不闻者乎
学生独立解决问题。然后小组交流,弄清疑点,注意纠错。
为善不积邪?安有不闻者乎
助教策略
(学习随笔)
方法指导:独立完成后,小组内的对子间互相用红笔互改,有疑问的由组长组织讨论订正。
故不登高山,不知天之高也
