13.2三角形全等的条件3(上课)[上学期]
文档属性
| 名称 | 13.2三角形全等的条件3(上课)[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 312.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-10-29 12:20:00 | ||
图片预览






文档简介
课件14张PPT。13.2 全等三角形条件3全等三角形判定定理:(1)边边边(SSS)
(2)两边夹角(SAS)(3)两角一边(角边角、角角边)
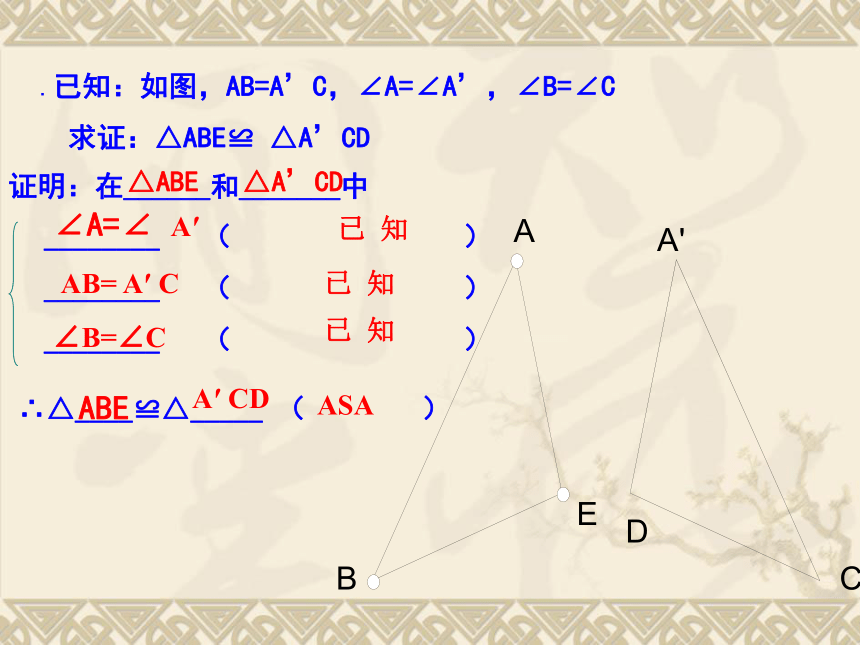
(4)三组角 先任意画出一个△ABC,再画一个△A/B/C/,使A/B/=AB,∠A/ =∠A,∠B/ =∠B 。把画好的△A/B/C/剪下,放到△ABC上,它们全等吗?探究1全等判定定理3:有两角和它们夹边对应相等的两个三角形全等(简写成“角边角”或“ASA”)。从探究中你发现了什么规律:.已知:如图,AB=A’C,∠A=∠A’,∠B=∠C
求证:△ABE≌ △A’CD ∠A=∠ A′△ABE △A’CD ABEAB= A′ C∠B=∠C
ASA
A′ CD
已 知已 知已 知
在△ABC和△DEF中,∠A=∠D, ∠B=∠E ,BC=EF,△ABC与△DEF全等吗?能利用角边角条件证明你的结论吗?探究2全等判定定理4:有两角和其中一个角的对边对应相等的两个三角形全等(简写成“角角边”或“AAS”)。从探究中你发现了什么规律:
两角一边,这一边不是其中一角的对边可以证明全等吗?
小结:证明三角形全等的方法有哪些?全等判定定理1:有三边对应相等的两个三角形全等(简写成“边边边”或“SSS”)。全等判定定理2:有两边和它们夹角对应相等的两个三角形全等(简写成“边角边”或“SAS”)。全等判定定理3:有两角和它们夹边对应相等的两个三角形全等(简写成“角边角”或“ASA”)。全等判定定理4:有两角和其中一个角的对边对应相等的两个三角形全等(简写成“角角边”或“AAS”)。全等三角形判定定理:(1)边边边(SSS)
(2)边角边(SAS)
(3)角边角(ASA)
(4)角角边(AAS)例题讲解: (2)如图, 在AB、AC上各取一点E、D,使AE=AD,连结BD、CE,相交于点O,连结AO,若∠1= ∠2 ,求证∠B= ∠C。 ABCDE12O (3)如图, CE⊥AB于点E,BD ⊥AC于D,且∠1= ∠2 ,求证:BE=CD。 练习:P101 补充题:
如图,已知∠1=∠2,∠3=∠4,BD=CE
求证:AB=AC (2)如图,两条直线AC、BD相交于点O,BO=DO,CO=AO,直线EF过点O,且分别交AB、DC于点E、F,求证:OE=OFABCDEFO 2、如图,两条直线AC、BD相交于点O,△ABO≌ △CDO,BE//DF,求证:BE=DF3、已知:如图,△ABC≌△A′B′C′,
AD、A′D′分别是△ABC和△A′B′C′的高.
求证:AD = A′D′See You!
(2)两边夹角(SAS)(3)两角一边(角边角、角角边)
(4)三组角 先任意画出一个△ABC,再画一个△A/B/C/,使A/B/=AB,∠A/ =∠A,∠B/ =∠B 。把画好的△A/B/C/剪下,放到△ABC上,它们全等吗?探究1全等判定定理3:有两角和它们夹边对应相等的两个三角形全等(简写成“角边角”或“ASA”)。从探究中你发现了什么规律:.已知:如图,AB=A’C,∠A=∠A’,∠B=∠C
求证:△ABE≌ △A’CD ∠A=∠ A′△ABE △A’CD ABEAB= A′ C∠B=∠C
ASA
A′ CD
已 知已 知已 知
在△ABC和△DEF中,∠A=∠D, ∠B=∠E ,BC=EF,△ABC与△DEF全等吗?能利用角边角条件证明你的结论吗?探究2全等判定定理4:有两角和其中一个角的对边对应相等的两个三角形全等(简写成“角角边”或“AAS”)。从探究中你发现了什么规律:
两角一边,这一边不是其中一角的对边可以证明全等吗?
小结:证明三角形全等的方法有哪些?全等判定定理1:有三边对应相等的两个三角形全等(简写成“边边边”或“SSS”)。全等判定定理2:有两边和它们夹角对应相等的两个三角形全等(简写成“边角边”或“SAS”)。全等判定定理3:有两角和它们夹边对应相等的两个三角形全等(简写成“角边角”或“ASA”)。全等判定定理4:有两角和其中一个角的对边对应相等的两个三角形全等(简写成“角角边”或“AAS”)。全等三角形判定定理:(1)边边边(SSS)
(2)边角边(SAS)
(3)角边角(ASA)
(4)角角边(AAS)例题讲解: (2)如图, 在AB、AC上各取一点E、D,使AE=AD,连结BD、CE,相交于点O,连结AO,若∠1= ∠2 ,求证∠B= ∠C。 ABCDE12O (3)如图, CE⊥AB于点E,BD ⊥AC于D,且∠1= ∠2 ,求证:BE=CD。 练习:P101 补充题:
如图,已知∠1=∠2,∠3=∠4,BD=CE
求证:AB=AC (2)如图,两条直线AC、BD相交于点O,BO=DO,CO=AO,直线EF过点O,且分别交AB、DC于点E、F,求证:OE=OFABCDEFO 2、如图,两条直线AC、BD相交于点O,△ABO≌ △CDO,BE//DF,求证:BE=DF3、已知:如图,△ABC≌△A′B′C′,
AD、A′D′分别是△ABC和△A′B′C′的高.
求证:AD = A′D′See You!
