三角形全等的条件及其性质[上学期]
文档属性
| 名称 | 三角形全等的条件及其性质[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 206.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-11-10 18:52:00 | ||
图片预览



文档简介
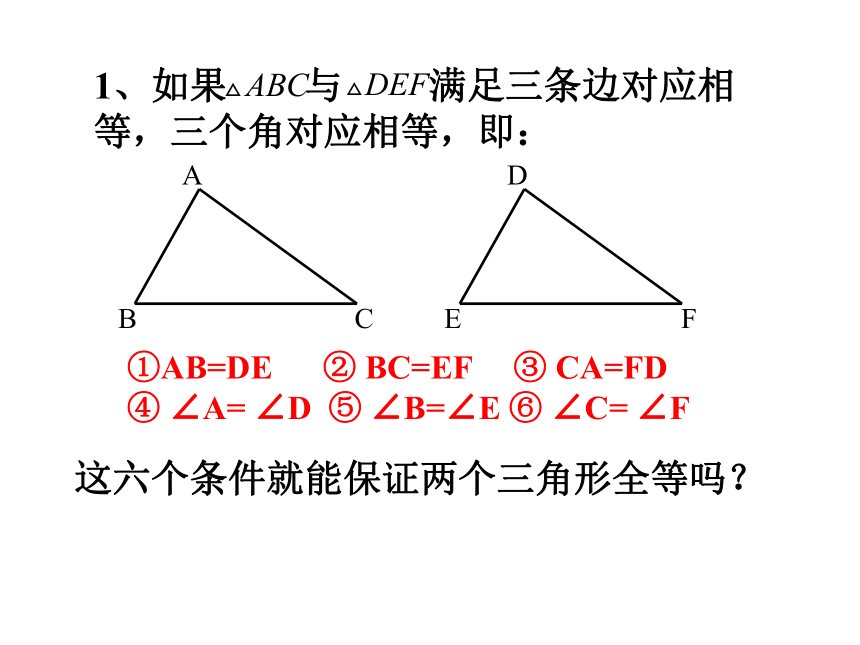
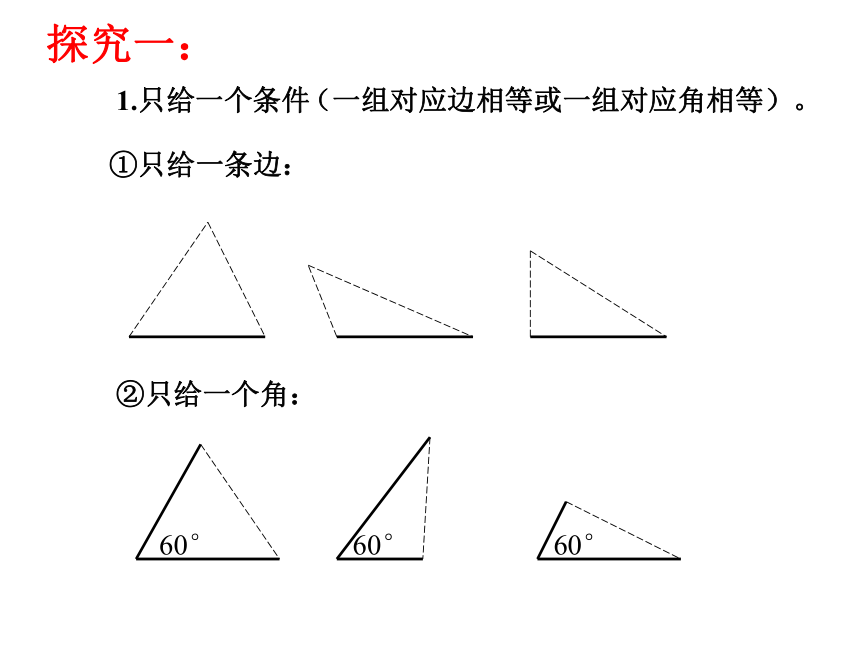
课件16张PPT。13.2 三角形全等的条件(一)临海中学初二数学备课组①AB=DE ② BC=EF ③ CA=FD ④ ∠A= ∠D ⑤ ∠B=∠E ⑥ ∠C= ∠F1、如果 与 满足三条边对应相等,三个角对应相等,即:这六个条件就能保证两个三角形全等吗?1.只给一个条件①只给一条边:②只给一个角:探究一:(一组对应边相等或一组对应角相等)。
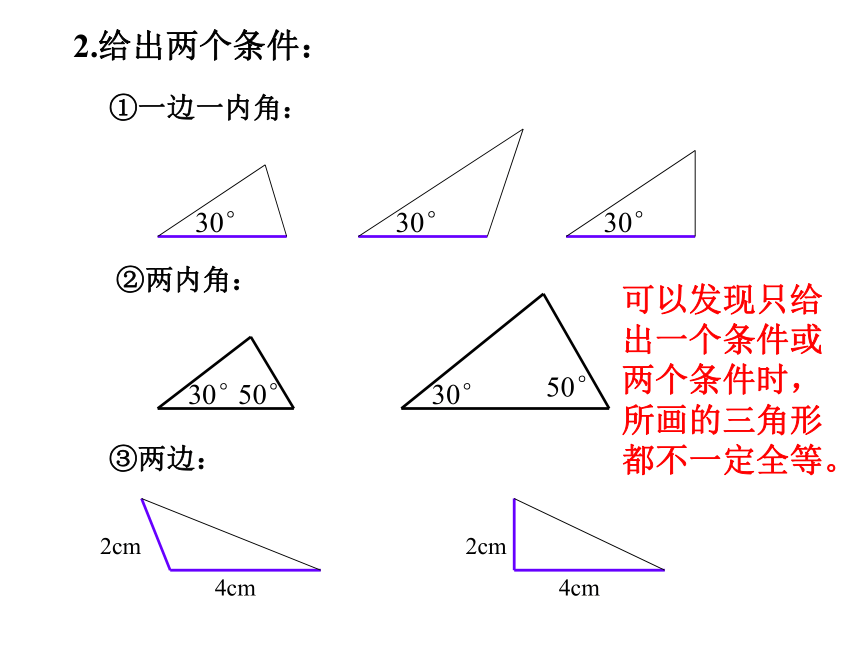
2.给出两个条件:①一边一内角:②两内角:③两边:可以发现只给出一个条件或两个条件时,所画的三角形都不一定全等。3.满足上述条件中的三个条件,能保证 与三条边三个角两角一边两边一角全等吗?我们可以分情况讨论,有哪几种情况?探究二先任意画一个 ,再画 ,使AB=DE,BC=EF,CA=FD,你能画出满足上述条件的 吗?把画好的 剪下,放到 上,它们全等吗?上面的探究反映了什么规律?1、画线段EF= BC。2、分别以E、F为圆心,线段AB,AC为半径画弧,两弧交于点D3、连结DE,DF。△ DEF就是所求的三角形画法: 有三边对应相等的两个三角形全等.
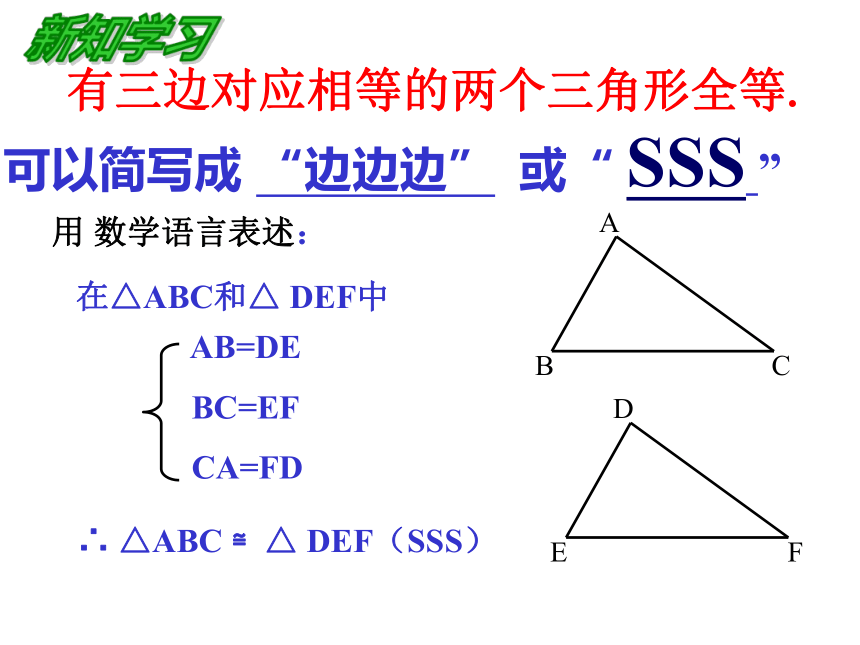
可以简写成 “边边边” 或“ SSS ” 用 数学语言表述:在△ABC和△ DEF中∴ △ABC ≌△ DEF(SSS)新知学习 判断两个三角形全等的推理过程,叫做证明三角形全等。议一议:在下列推理中填写需要补充的条件,使结论成立:
如图,在△AOB和△DOC中∴ △AOB≌△DOC(SSS)解: △ABC≌△DCB
理由如下:
AB = CD
AC = DB
=
SSS △DCBBCCBBF=CD或 BD=CF应用迁移,巩固提高例1. 如下图,△ABC是一个刚架,AB=AC,AD是连接A与BC中点D的支架。 求证:△ ABD≌ △ ACD分析:要证明△ ABD≌ △ ACD,首先看这两个三角形的三条边是否对应相等。结论:从这题的证明中可以看出,证明是由题设(已知)出发,经过一步步的推理,最后推出结论正确的过程。归纳:①准备条件:证全等时要用的间接条件要先证好;②三角形全等书写三步骤:写出在哪两个三角形中摆出三个条件用大括号括起来写出全等结论证明的书写步骤:(SSS)拓展与提高:如图,在四边形ABCD中
AB=CD,AD=BC,则∠A= ∠C
请说明理由。AB=CD (已知)AD=BC (已知)BD=DB(公共边)∴ ∠A= ∠C ( )
全等三角形的对应角相等小结2. 三边对应相等的两个三角形全等(边边边或SSS);1.知道三角形三条边的长度怎样画三角形。3、体验分类讨论的数学思想4、初步学会理解证明的思路作业A.作业本1-4题及画一个三角形,是它的三边分别为3cm,4cm,3cm和习题精选P88 6题B.作业本1-4题及画一个三角形,是它的三边分别为3cm,4cm,3cm和习题精选P88 8题C.作业本1-4,6,7题及画一个三角形,是它的三边分别为3cm,4cm,3cm再 见已知: 如图,AC=AD ,BC=BD. 求证: ∠C=∠D.ABCD解:在△ACB 和 △ADB中 AC = A D
BC = BD
A B = A B (公共边)∴△ACB≌△ADB(SSS)议一议:连结AB∴∠C=∠D.(全等三角形对应角相等)
2.给出两个条件:①一边一内角:②两内角:③两边:可以发现只给出一个条件或两个条件时,所画的三角形都不一定全等。3.满足上述条件中的三个条件,能保证 与三条边三个角两角一边两边一角全等吗?我们可以分情况讨论,有哪几种情况?探究二先任意画一个 ,再画 ,使AB=DE,BC=EF,CA=FD,你能画出满足上述条件的 吗?把画好的 剪下,放到 上,它们全等吗?上面的探究反映了什么规律?1、画线段EF= BC。2、分别以E、F为圆心,线段AB,AC为半径画弧,两弧交于点D3、连结DE,DF。△ DEF就是所求的三角形画法: 有三边对应相等的两个三角形全等.
可以简写成 “边边边” 或“ SSS ” 用 数学语言表述:在△ABC和△ DEF中∴ △ABC ≌△ DEF(SSS)新知学习 判断两个三角形全等的推理过程,叫做证明三角形全等。议一议:在下列推理中填写需要补充的条件,使结论成立:
如图,在△AOB和△DOC中∴ △AOB≌△DOC(SSS)解: △ABC≌△DCB
理由如下:
AB = CD
AC = DB
=
SSS △DCBBCCBBF=CD或 BD=CF应用迁移,巩固提高例1. 如下图,△ABC是一个刚架,AB=AC,AD是连接A与BC中点D的支架。 求证:△ ABD≌ △ ACD分析:要证明△ ABD≌ △ ACD,首先看这两个三角形的三条边是否对应相等。结论:从这题的证明中可以看出,证明是由题设(已知)出发,经过一步步的推理,最后推出结论正确的过程。归纳:①准备条件:证全等时要用的间接条件要先证好;②三角形全等书写三步骤:写出在哪两个三角形中摆出三个条件用大括号括起来写出全等结论证明的书写步骤:(SSS)拓展与提高:如图,在四边形ABCD中
AB=CD,AD=BC,则∠A= ∠C
请说明理由。AB=CD (已知)AD=BC (已知)BD=DB(公共边)∴ ∠A= ∠C ( )
全等三角形的对应角相等小结2. 三边对应相等的两个三角形全等(边边边或SSS);1.知道三角形三条边的长度怎样画三角形。3、体验分类讨论的数学思想4、初步学会理解证明的思路作业A.作业本1-4题及画一个三角形,是它的三边分别为3cm,4cm,3cm和习题精选P88 6题B.作业本1-4题及画一个三角形,是它的三边分别为3cm,4cm,3cm和习题精选P88 8题C.作业本1-4,6,7题及画一个三角形,是它的三边分别为3cm,4cm,3cm再 见已知: 如图,AC=AD ,BC=BD. 求证: ∠C=∠D.ABCD解:在△ACB 和 △ADB中 AC = A D
BC = BD
A B = A B (公共边)∴△ACB≌△ADB(SSS)议一议:连结AB∴∠C=∠D.(全等三角形对应角相等)
