三角形全等的条件(四)[下学期]
文档属性
| 名称 | 三角形全等的条件(四)[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 895.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-11-20 00:00:00 | ||
图片预览


文档简介
课件15张PPT。13.2探索三角形全等的条件路桥实验中学 王万丰
2006.11.21尺规作图的方法步骤:1、画∠DC/E= 90°.
2、在射线C/ D上截取C/B/=CB.
3、以B/为圆心,以AB为半径画弧,交 射线C/E于点A/.
4、连结B/A/。已知Rt△ABC,∠C=90°。
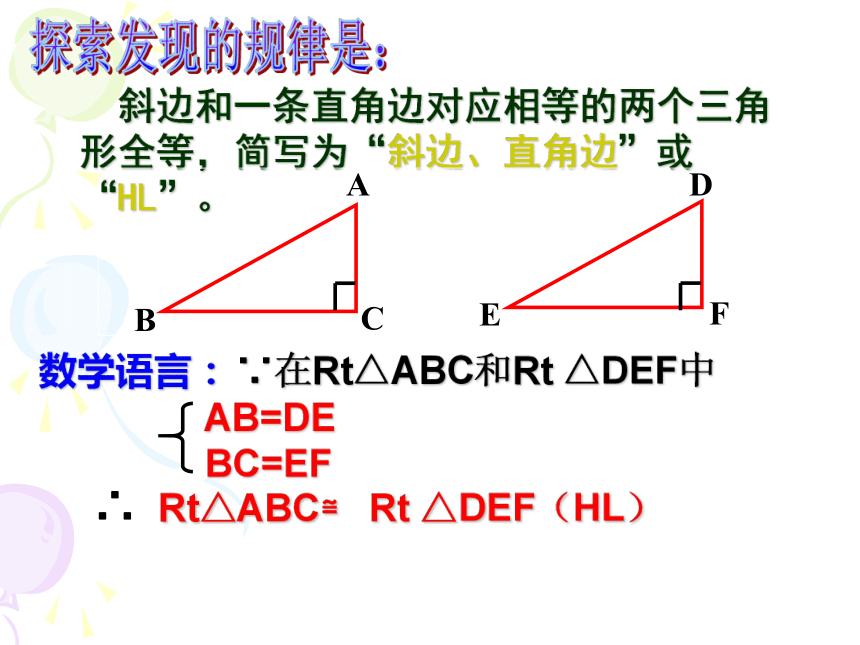
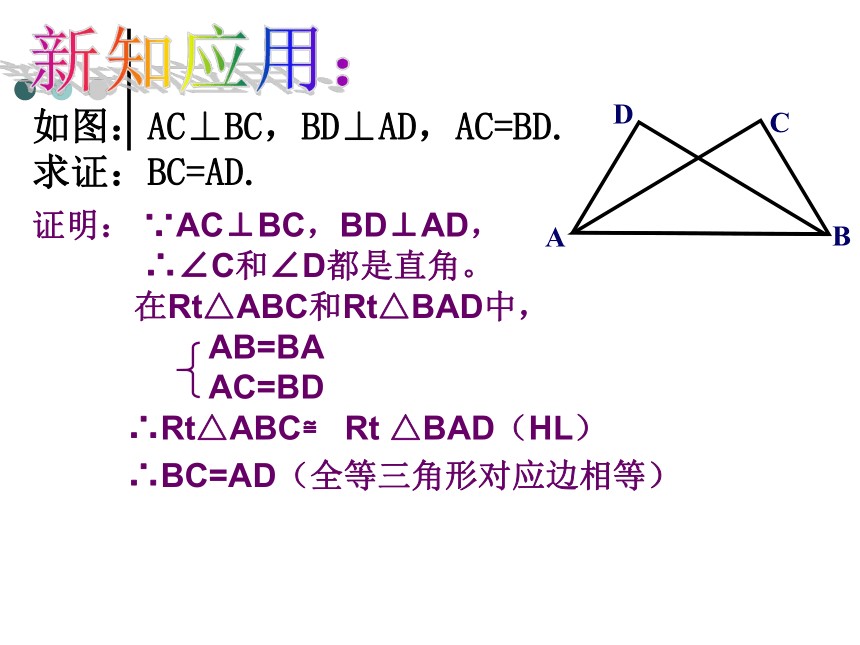
作Rt△A′B′C′ ,使得∠C′=∠C=90°,斜边和任意一条直角边对应相等。探 究 探索发现的规律是: 斜边和一条直角边对应相等的两个三角形全等,简写为“斜边、直角边”或“HL”。数学语言:∵在Rt△ABC和Rt △DEF中如图:AC⊥BC,BD⊥AD,AC=BD.
求证:BC=AD.ABCD证明: ∵AC⊥BC,BD⊥AD,
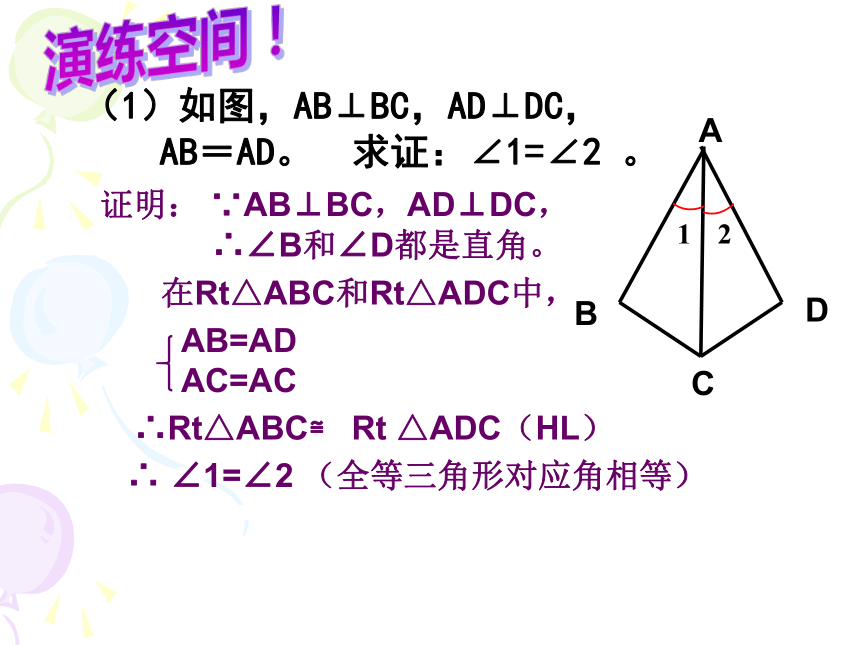
∴∠C和∠D都是直角。在Rt△ABC和Rt△BAD中,∴Rt△ABC≌ Rt △BAD(HL)∴BC=AD(全等三角形对应边相等)新知应用:(1)如图,AB⊥BC,AD⊥DC,
AB=AD。 求证:∠1=∠2 。证明: ∵AB⊥BC,AD⊥DC,
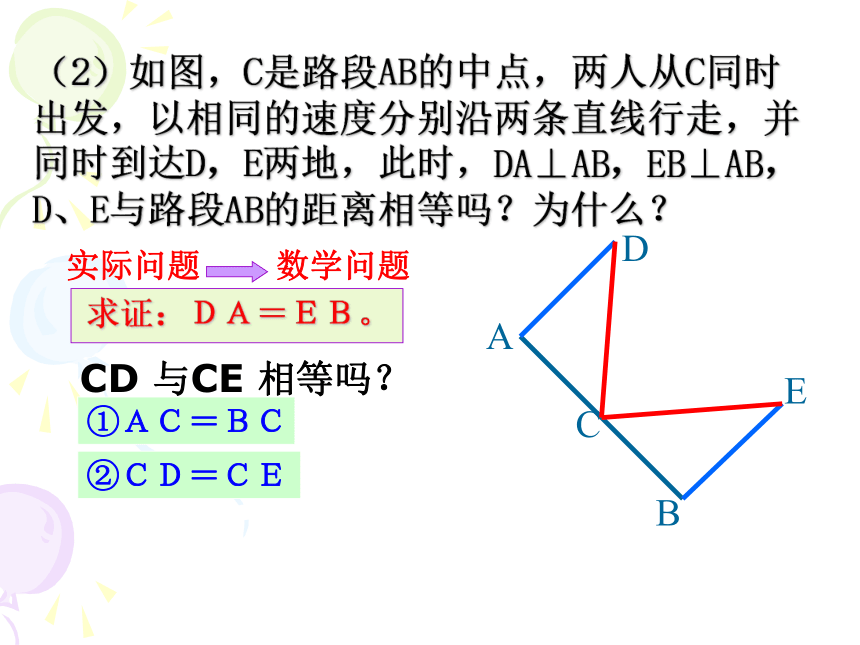
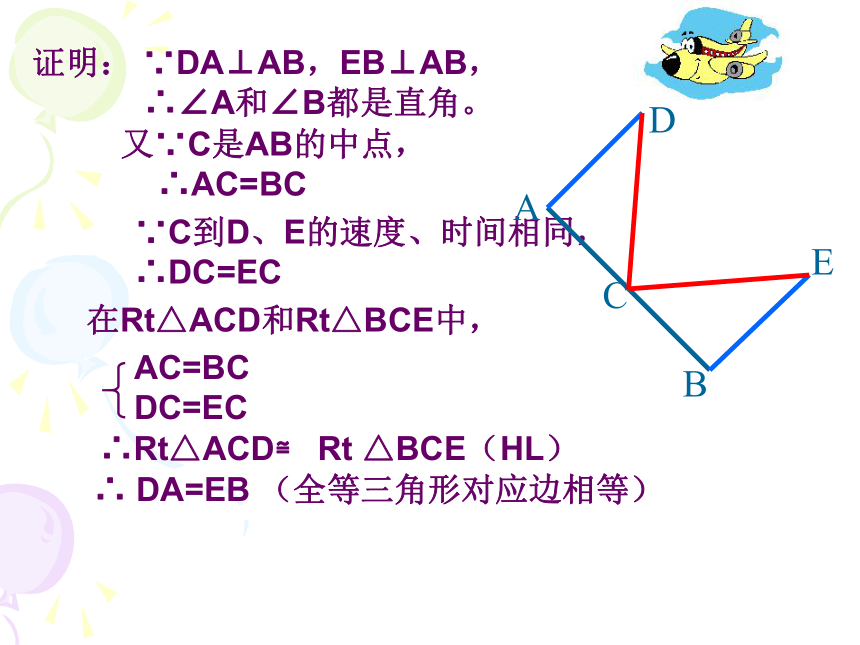
∴∠B和∠D都是直角。∴Rt△ABC≌ Rt △ADC(HL)∴ ∠1=∠2 (全等三角形对应角相等)在Rt△ABC和Rt△ADC中,演练空间!(2)如图,C是路段AB的中点,两人从C同时出发,以相同的速度分别沿两条直线行走,并同时到达D,E两地,此时,DA⊥AB,EB⊥AB,D、E与路段AB的距离相等吗?为什么?CD 与CE 相等吗?证明: ∵DA⊥AB,EB⊥AB,
∴∠A和∠B都是直角。∴Rt△ACD≌ Rt △BCE(HL)∴ DA=EB (全等三角形对应边相等)在Rt△ACD和Rt△BCE中,又∵C是AB的中点,
∴AC=BC ∵C到D、E的速度、时间相同,
∴DC=EC(3)如图,AB=CD,AE⊥BC,DF⊥BC,
CE=BF.求证:AE=DF.证明:∵ AE⊥BC,DF⊥BC
∴△ABE和△DCF都是直角三角形。又∵CE=BF ∴CE-EF=BF-EF
即CF=BE。 在Rt△ABE和Rt△DCF中∴Rt△ABE≌Rt△DCF(HL) ∴AE=DF
斜边和一条直角边对应相等的两个直角三角形全等(HL).畅所欲言! (1)如图,两根长度为12米的绳子,一端系在旗杆上,另一端分别固定在地面两个木桩上,两个木桩离旗杆底部的距离相等吗?请说明你的理由。拓展探究1 (2)如图,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠ABC和∠DFE大小有什么关系?拓展探究2解:在Rt△ABC和Rt△DEF中,∴ Rt△ABC≌Rt△DEF (HL).∴∠ABC=∠DEF
(全等三角形对应角相等).∵ ∠DEF+∠DFE=90°,∴∠ABC+∠DFE=90°. 如图,E,F分别为线段AC上的两个点,且DE⊥AC于E点,BF⊥AC于F点,若AB=CD,AF=CE,BD交AC于M点.求证:MB=MD, ME=MF。ABCDEFM拓 展 探 究 3如图,在矩形ABCD中,F是BC边上一点,AF的延长线交DC的延长线于点G,DE⊥AG于E,且DE=AB,∠1=∠2.根据上述条件,请在图中找出一对全等三角形,并证明你的结论. 课后思考题再 见
2006.11.21尺规作图的方法步骤:1、画∠DC/E= 90°.
2、在射线C/ D上截取C/B/=CB.
3、以B/为圆心,以AB为半径画弧,交 射线C/E于点A/.
4、连结B/A/。已知Rt△ABC,∠C=90°。
作Rt△A′B′C′ ,使得∠C′=∠C=90°,斜边和任意一条直角边对应相等。探 究 探索发现的规律是: 斜边和一条直角边对应相等的两个三角形全等,简写为“斜边、直角边”或“HL”。数学语言:∵在Rt△ABC和Rt △DEF中如图:AC⊥BC,BD⊥AD,AC=BD.
求证:BC=AD.ABCD证明: ∵AC⊥BC,BD⊥AD,
∴∠C和∠D都是直角。在Rt△ABC和Rt△BAD中,∴Rt△ABC≌ Rt △BAD(HL)∴BC=AD(全等三角形对应边相等)新知应用:(1)如图,AB⊥BC,AD⊥DC,
AB=AD。 求证:∠1=∠2 。证明: ∵AB⊥BC,AD⊥DC,
∴∠B和∠D都是直角。∴Rt△ABC≌ Rt △ADC(HL)∴ ∠1=∠2 (全等三角形对应角相等)在Rt△ABC和Rt△ADC中,演练空间!(2)如图,C是路段AB的中点,两人从C同时出发,以相同的速度分别沿两条直线行走,并同时到达D,E两地,此时,DA⊥AB,EB⊥AB,D、E与路段AB的距离相等吗?为什么?CD 与CE 相等吗?证明: ∵DA⊥AB,EB⊥AB,
∴∠A和∠B都是直角。∴Rt△ACD≌ Rt △BCE(HL)∴ DA=EB (全等三角形对应边相等)在Rt△ACD和Rt△BCE中,又∵C是AB的中点,
∴AC=BC ∵C到D、E的速度、时间相同,
∴DC=EC(3)如图,AB=CD,AE⊥BC,DF⊥BC,
CE=BF.求证:AE=DF.证明:∵ AE⊥BC,DF⊥BC
∴△ABE和△DCF都是直角三角形。又∵CE=BF ∴CE-EF=BF-EF
即CF=BE。 在Rt△ABE和Rt△DCF中∴Rt△ABE≌Rt△DCF(HL) ∴AE=DF
斜边和一条直角边对应相等的两个直角三角形全等(HL).畅所欲言! (1)如图,两根长度为12米的绳子,一端系在旗杆上,另一端分别固定在地面两个木桩上,两个木桩离旗杆底部的距离相等吗?请说明你的理由。拓展探究1 (2)如图,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠ABC和∠DFE大小有什么关系?拓展探究2解:在Rt△ABC和Rt△DEF中,∴ Rt△ABC≌Rt△DEF (HL).∴∠ABC=∠DEF
(全等三角形对应角相等).∵ ∠DEF+∠DFE=90°,∴∠ABC+∠DFE=90°. 如图,E,F分别为线段AC上的两个点,且DE⊥AC于E点,BF⊥AC于F点,若AB=CD,AF=CE,BD交AC于M点.求证:MB=MD, ME=MF。ABCDEFM拓 展 探 究 3如图,在矩形ABCD中,F是BC边上一点,AF的延长线交DC的延长线于点G,DE⊥AG于E,且DE=AB,∠1=∠2.根据上述条件,请在图中找出一对全等三角形,并证明你的结论. 课后思考题再 见
