三角形全等的条件(三)[上学期]
文档属性
| 名称 | 三角形全等的条件(三)[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 30.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-11-21 00:00:00 | ||
图片预览

文档简介
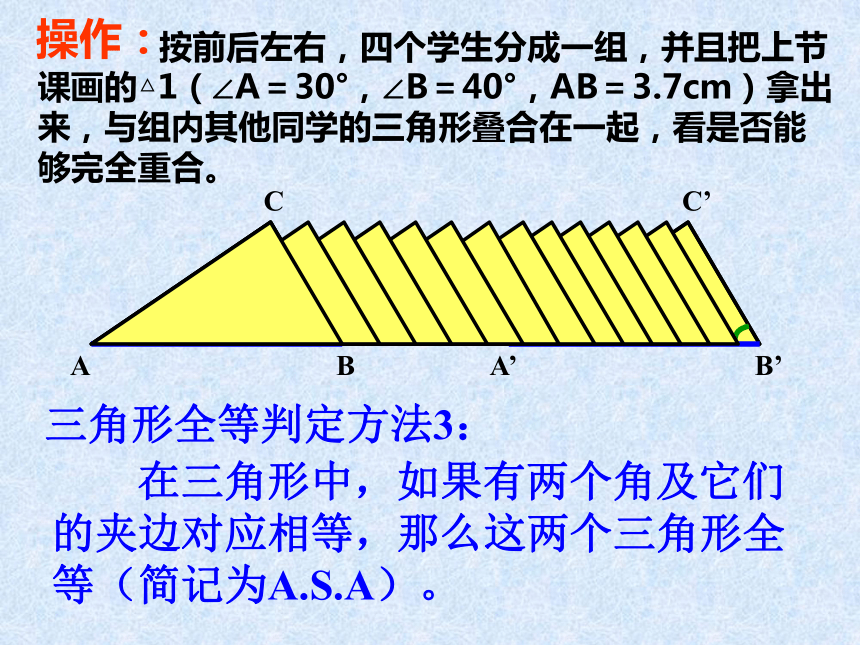
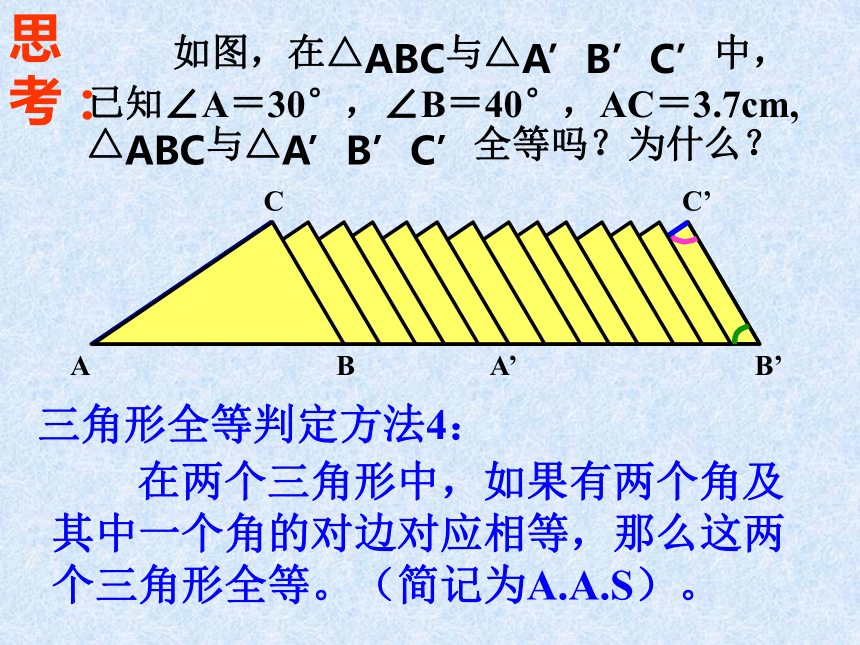
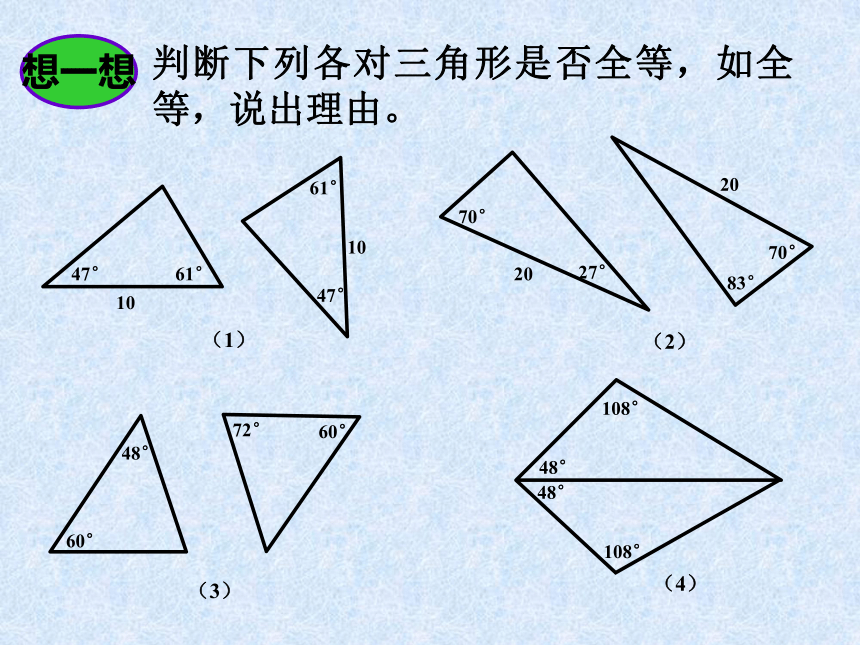
课件14张PPT。13.2三角形全等的判定3(角、边、角)(角、角、边)ABCA’B’C’操作: 按前后左右,四个学生分成一组,并且把上节课画的△1(∠A=30°,∠B=40°,AB=3.7cm)拿出来,与组内其他同学的三角形叠合在一起,看是否能够完全重合。 三角形全等判定方法3: 在三角形中,如果有两个角及它们的夹边对应相等,那么这两个三角形全等(简记为A.S.A)。 ABCA’B’C’思考: 如图,在△ABC与△A’B’C’中,已知∠A=30°,∠B=40°,AC=3.7cm, △ABC与△A’B’C’全等吗?为什么? 三角形全等判定方法4: 在两个三角形中,如果有两个角及其中一个角的对边对应相等,那么这两个三角形全等。(简记为A.A.S)。 判断下列各对三角形是否全等,如全等,说出理由。想一想47°47°61°61°1010(1)(2)83°27°70°70°2020(3)60°60°72°48°(4)48°48°108°108°在△AOC和△BOD中,
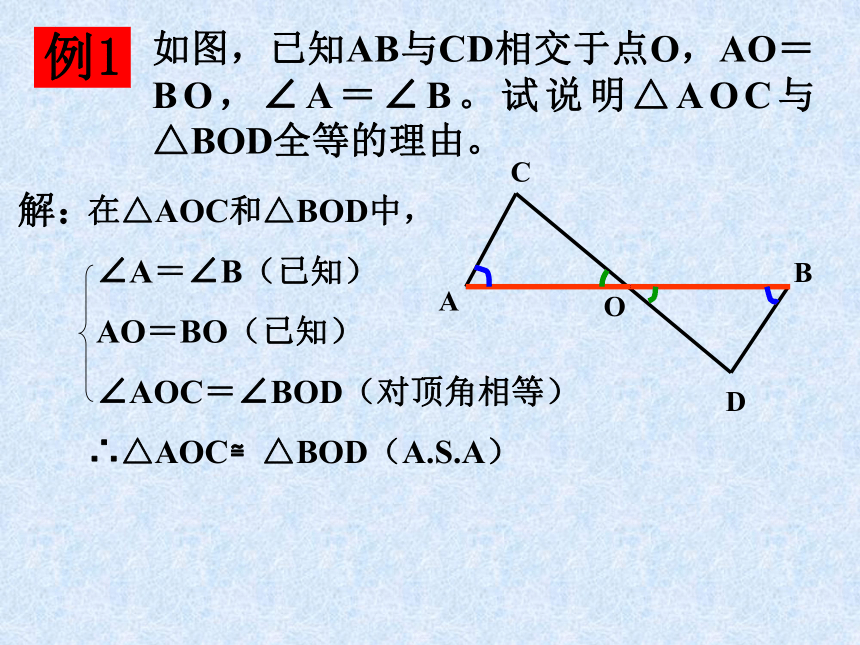
∠A=∠B(已知)
AO=BO(已知)
∠AOC=∠BOD(对顶角相等)
∴△AOC≌△BOD(A.S.A)
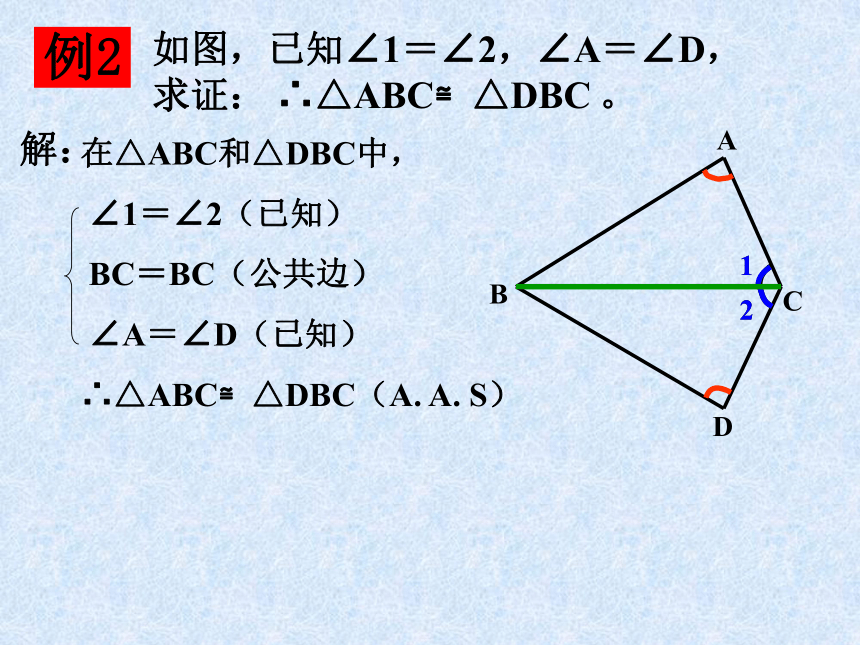
如图,已知AB与CD相交于点O,AO=BO,∠A=∠B。试说明△AOC与△BOD全等的理由。 DABCO解:例121在△ABC和△DBC中,
∠1=∠2(已知)
BC=BC(公共边)
∠A=∠D(已知)
∴△ABC≌△DBC(A. A. S)
如图,已知∠1=∠2,∠A=∠D,
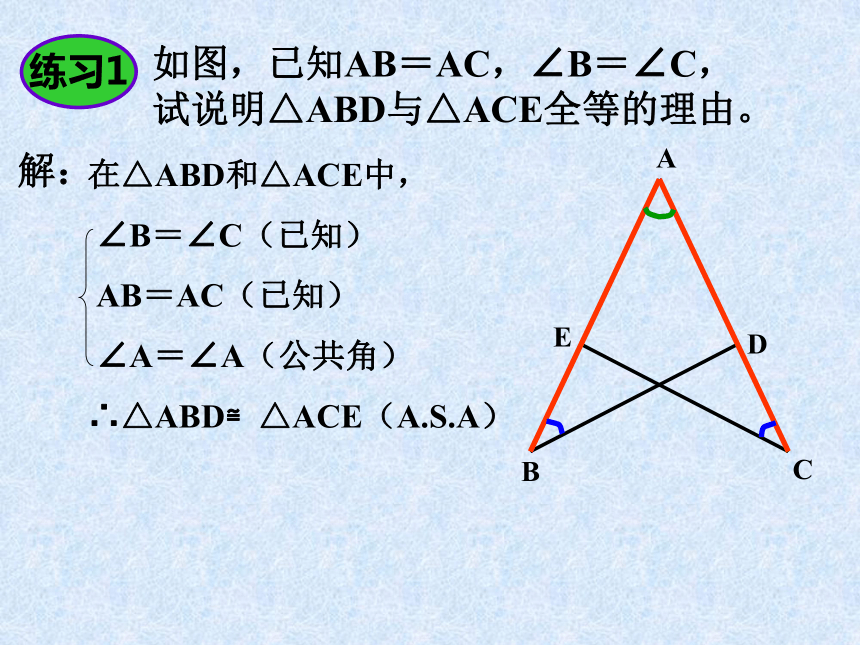
求证: ∴△ABC≌△DBC 。 DABC1解:例22在△ABD和△ACE中,
∠B=∠C(已知)
AB=AC(已知)
∠A=∠A(公共角)
∴△ABD≌△ACE(A.S.A)
如图,已知AB=AC,∠B=∠C,
试说明△ABD与△ACE全等的理由。 D解:练习1ACBE在△AOC和△DOB中,
∠A=∠D(已知)
CO=BO(已知)
∠1=∠2(对顶角相等)
∴△AOC≌△DOB( A. A. S)如图,已知AB与CD相交于O,∠A=∠D,CO=BO,试说明△AOC与△DOB全等的理由。 D解:练习2ACBO12等,经常隐含在图形中。你发现了吗?公共边; 对顶角 公共角; ABCDE12 如图,已知∠C=∠E,∠1=∠2,AB=AD,
求证:△ABC≌△ADE
证明: ∵∠1=∠2(已知) ∴∠1+∠DAC=∠2+∠DAC 即∠BAC=∠DAE
∴ △ABC≌△ADE(AAS)在△ABC和△ADC 中如图,∠ABC=∠DCB,∠ACB=∠DBC,试说明△ABC与△DCB全等的理由。 练习5ABCD课堂小结:
1)两角和它们的夹边对应相等的两个三角形全等(ASA);
2)两角和其中一角的对边对应相等的两个三角形全等(AAS)。
作业:谢谢各位莅临指导!
∠A=∠B(已知)
AO=BO(已知)
∠AOC=∠BOD(对顶角相等)
∴△AOC≌△BOD(A.S.A)
如图,已知AB与CD相交于点O,AO=BO,∠A=∠B。试说明△AOC与△BOD全等的理由。 DABCO解:例121在△ABC和△DBC中,
∠1=∠2(已知)
BC=BC(公共边)
∠A=∠D(已知)
∴△ABC≌△DBC(A. A. S)
如图,已知∠1=∠2,∠A=∠D,
求证: ∴△ABC≌△DBC 。 DABC1解:例22在△ABD和△ACE中,
∠B=∠C(已知)
AB=AC(已知)
∠A=∠A(公共角)
∴△ABD≌△ACE(A.S.A)
如图,已知AB=AC,∠B=∠C,
试说明△ABD与△ACE全等的理由。 D解:练习1ACBE在△AOC和△DOB中,
∠A=∠D(已知)
CO=BO(已知)
∠1=∠2(对顶角相等)
∴△AOC≌△DOB( A. A. S)如图,已知AB与CD相交于O,∠A=∠D,CO=BO,试说明△AOC与△DOB全等的理由。 D解:练习2ACBO12等,经常隐含在图形中。你发现了吗?公共边; 对顶角 公共角; ABCDE12 如图,已知∠C=∠E,∠1=∠2,AB=AD,
求证:△ABC≌△ADE
证明: ∵∠1=∠2(已知) ∴∠1+∠DAC=∠2+∠DAC 即∠BAC=∠DAE
∴ △ABC≌△ADE(AAS)在△ABC和△ADC 中如图,∠ABC=∠DCB,∠ACB=∠DBC,试说明△ABC与△DCB全等的理由。 练习5ABCD课堂小结:
1)两角和它们的夹边对应相等的两个三角形全等(ASA);
2)两角和其中一角的对边对应相等的两个三角形全等(AAS)。
作业:谢谢各位莅临指导!
