三角形全等的条件(二)[下学期]
文档属性
| 名称 | 三角形全等的条件(二)[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 651.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-11-20 21:25:00 | ||
图片预览

文档简介
课件13张PPT。13.2 三角形全等的条件(2)路桥实验中学 王万丰
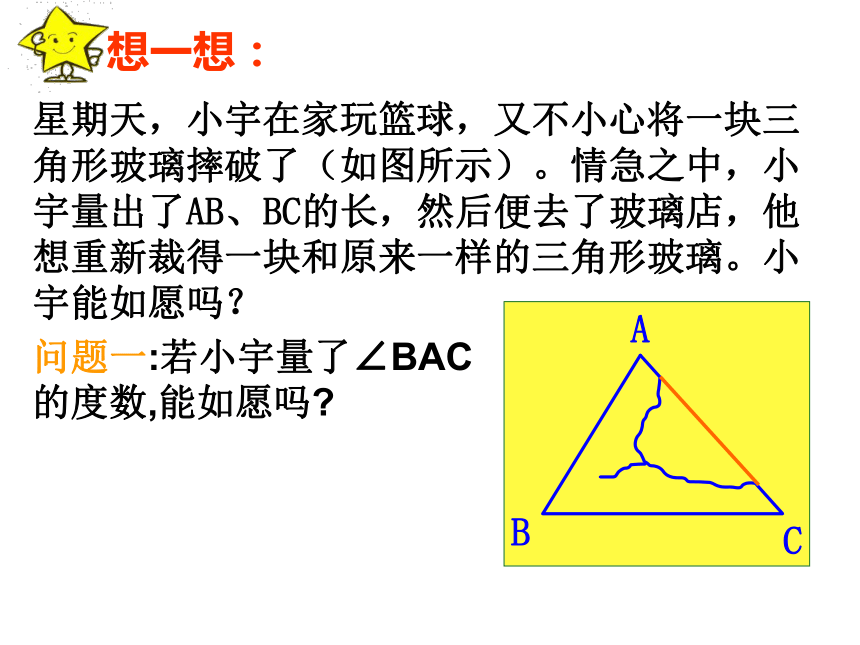
2006.11.17想一想:星期天,小宇在家玩篮球,又不小心将一块三角形玻璃摔破了(如图所示)。情急之中,小宇量出了AB、BC的长,然后便去了玻璃店,他想重新裁得一块和原来一样的三角形玻璃。小宇能如愿吗?问题一:若小宇量了∠BAC
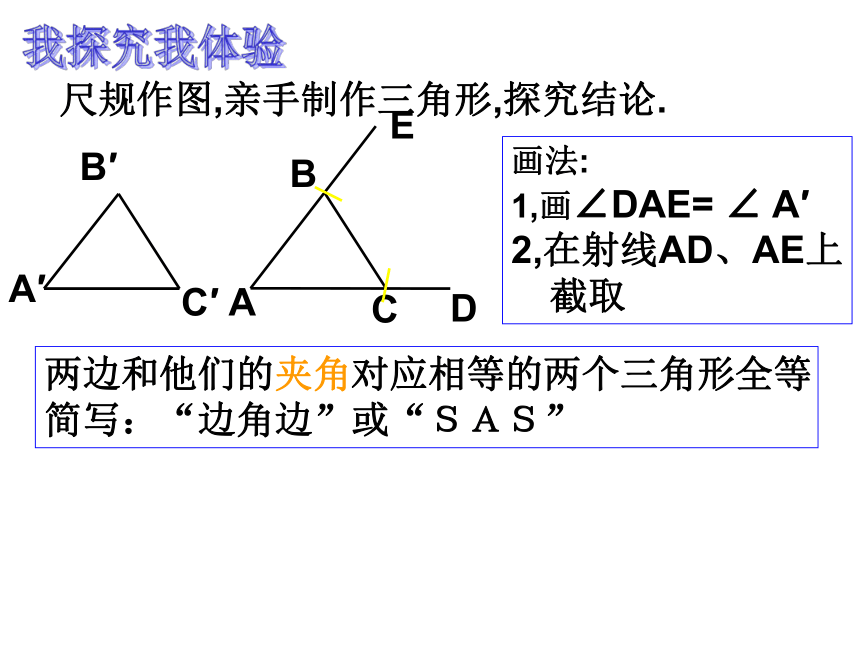
的度数,能如愿吗?尺规作图,亲手制作三角形,探究结论.A′B′C′ABCED画法:
1,画∠DAE= ∠ A′
2,在射线AD、AE上
截取两边和他们的夹角对应相等的两个三角形全等
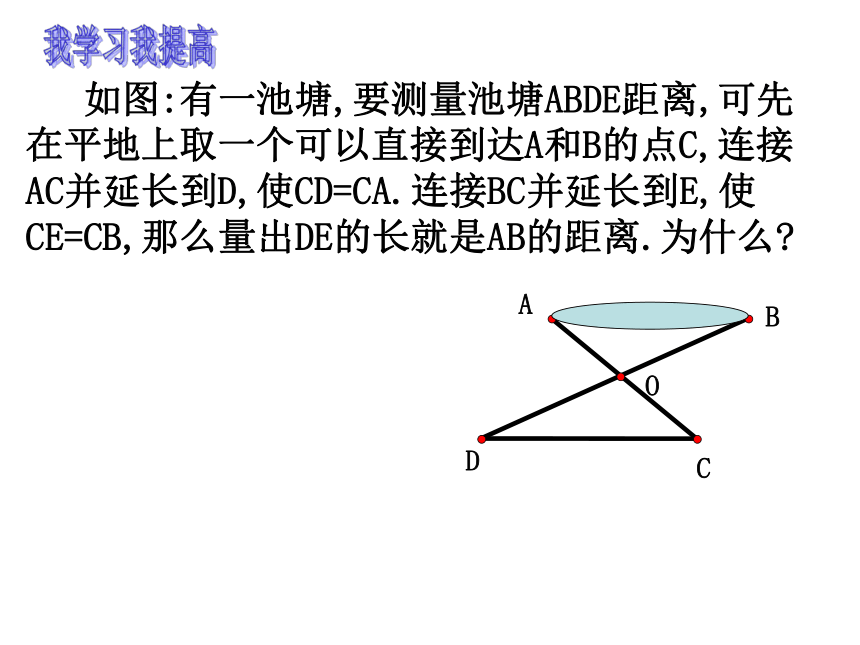
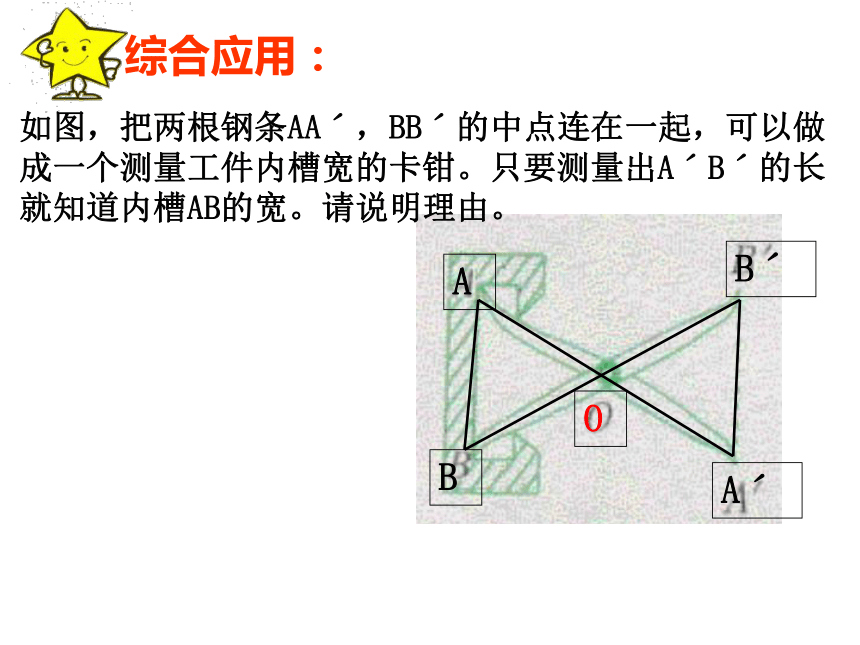
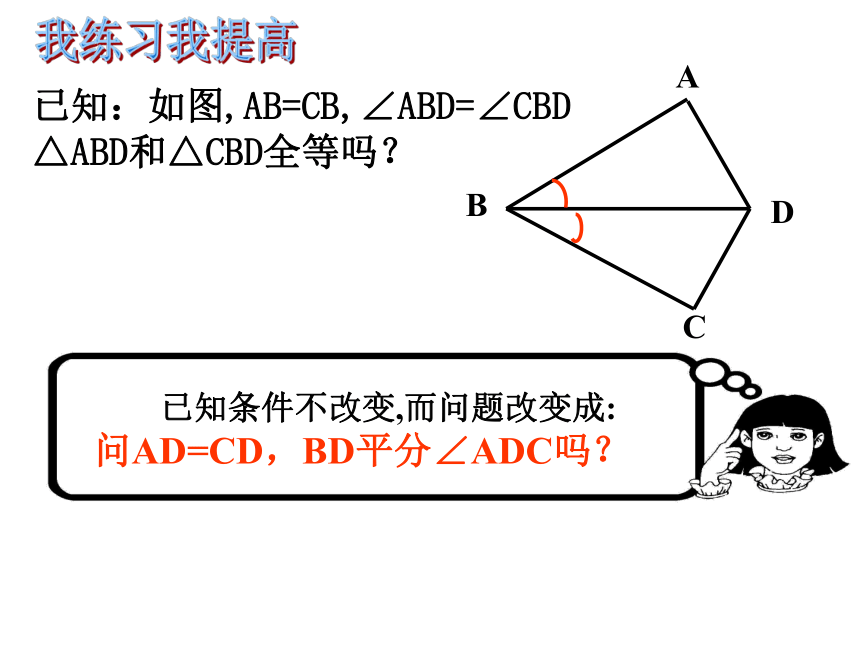
简写:“边角边”或“SAS”我探究我体验 如图:有一池塘,要测量池塘ABDE距离,可先在平地上取一个可以直接到达A和B的点C,连接AC并延长到D,使CD=CA.连接BC并延长到E,使CE=CB,那么量出DE的长就是AB的距离.为什么?我学习我提高综合应用:如图,把两根钢条AAˊ,BBˊ的中点连在一起,可以做成一个测量工件内槽宽的卡钳。只要测量出AˊBˊ的长就知道内槽AB的宽。请说明理由。已知:如图,AB=CB,∠ABD=∠CBD
△ABD和△CBD全等吗? 已知条件不改变,而问题改变成:
问AD=CD,BD平分∠ADC吗? 我练习我提高有两边和一个角对应相等的两个三角形全吗?注:这个角一定要是
这两边所夹的角我探究我聪明两边和他们的夹角对应相等的两个三角形全等
简写:“边角边”或“SAS”我自信我拓展 小明做了一个如图所示的风筝,其中∠EDH=∠FDH, ED=FD ,将上述条件标注在图中,小明不用测量就能知道EH=FH吗?与同桌进行交流。△EDH≌△FDH 根据“SAS”,所以EH=FH.
?
?
?
如图:A、B、C三点在一条直线上DA⊥AC,EC⊥AC,AB=CE,AD=CB.
求:∠DBE的度数我练习我提高解:如图,已知AB=DE,AC=DF,要说明△ABC≌△DEF,
还需增加一个什么条件?开放题 与同桌交流一下,然后请说一说,你本节课学习了些什么?1. 用尺规作图:已知两边及其夹角的三角形画三角形2. 三角形全等的条件,两边和它们的夹角对应相等的两个三角形全等 (边角边或SAS)3、会用SAS判定两个三角形全等总结与反思再见
2006.11.17想一想:星期天,小宇在家玩篮球,又不小心将一块三角形玻璃摔破了(如图所示)。情急之中,小宇量出了AB、BC的长,然后便去了玻璃店,他想重新裁得一块和原来一样的三角形玻璃。小宇能如愿吗?问题一:若小宇量了∠BAC
的度数,能如愿吗?尺规作图,亲手制作三角形,探究结论.A′B′C′ABCED画法:
1,画∠DAE= ∠ A′
2,在射线AD、AE上
截取两边和他们的夹角对应相等的两个三角形全等
简写:“边角边”或“SAS”我探究我体验 如图:有一池塘,要测量池塘ABDE距离,可先在平地上取一个可以直接到达A和B的点C,连接AC并延长到D,使CD=CA.连接BC并延长到E,使CE=CB,那么量出DE的长就是AB的距离.为什么?我学习我提高综合应用:如图,把两根钢条AAˊ,BBˊ的中点连在一起,可以做成一个测量工件内槽宽的卡钳。只要测量出AˊBˊ的长就知道内槽AB的宽。请说明理由。已知:如图,AB=CB,∠ABD=∠CBD
△ABD和△CBD全等吗? 已知条件不改变,而问题改变成:
问AD=CD,BD平分∠ADC吗? 我练习我提高有两边和一个角对应相等的两个三角形全吗?注:这个角一定要是
这两边所夹的角我探究我聪明两边和他们的夹角对应相等的两个三角形全等
简写:“边角边”或“SAS”我自信我拓展 小明做了一个如图所示的风筝,其中∠EDH=∠FDH, ED=FD ,将上述条件标注在图中,小明不用测量就能知道EH=FH吗?与同桌进行交流。△EDH≌△FDH 根据“SAS”,所以EH=FH.
?
?
?
如图:A、B、C三点在一条直线上DA⊥AC,EC⊥AC,AB=CE,AD=CB.
求:∠DBE的度数我练习我提高解:如图,已知AB=DE,AC=DF,要说明△ABC≌△DEF,
还需增加一个什么条件?开放题 与同桌交流一下,然后请说一说,你本节课学习了些什么?1. 用尺规作图:已知两边及其夹角的三角形画三角形2. 三角形全等的条件,两边和它们的夹角对应相等的两个三角形全等 (边角边或SAS)3、会用SAS判定两个三角形全等总结与反思再见
