三角形全等的条件(一)[下学期]
文档属性
| 名称 | 三角形全等的条件(一)[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 192.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-11-20 00:00:00 | ||
图片预览



文档简介
课件14张PPT。13.2三角形全等的条件(1)路桥实验中学 王万丰
20006.11.10(1)只给出一个条件(一条边或一个角)画三角形时,画出的三角形一定全等吗?有一条边对应相等的三角形不一定全等有一个角对应相等的三角形不一定全等做一做:(2)给出两个条件画三角形时,有几种可能的情况?每种情况下作出的三角形一定全等吗?不一定全等 只给出一个或两个条件时,都不能保证
所画的三角形一定全等,并且三个内角对
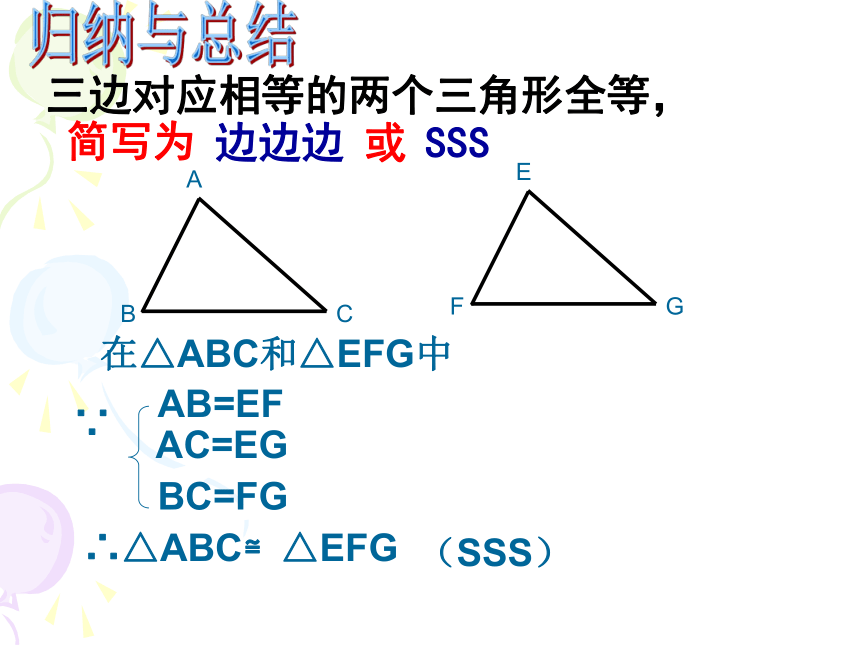
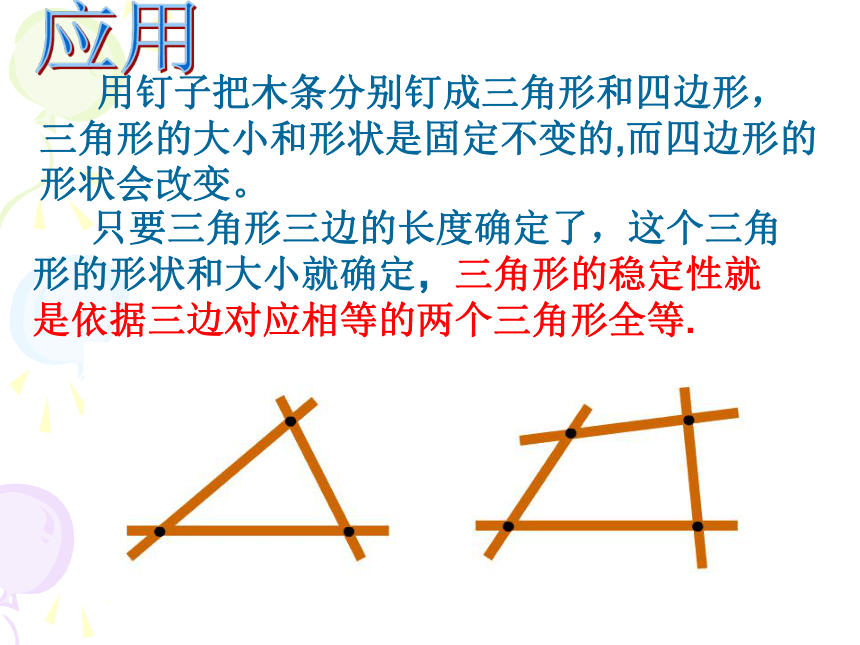
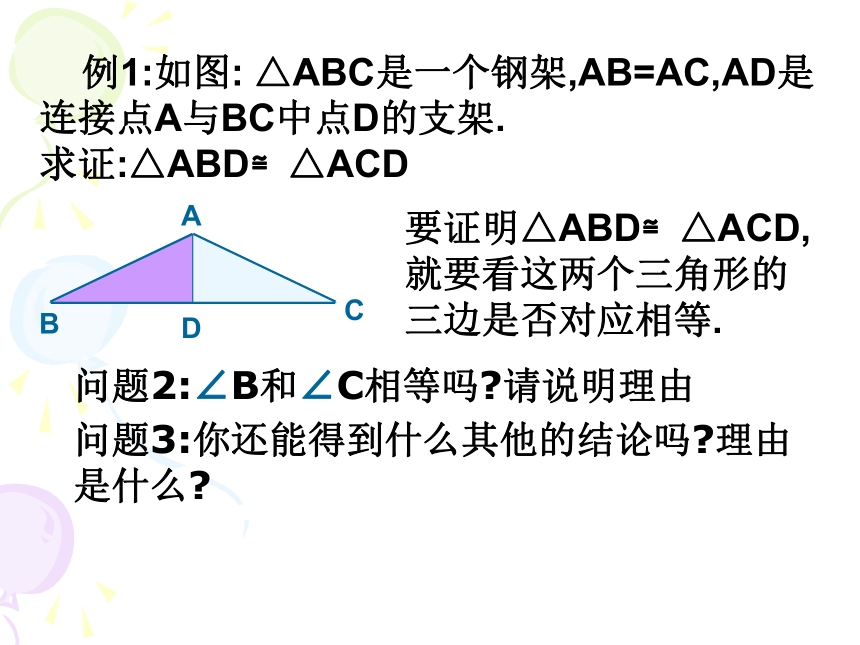
应相等的两个三角形也不一定全等。再探究∵在△ABC和△EFG中AB=EFAC=EGBC=FG∴△ABC≌△EFG(SSS)三边对应相等的两个三角形全等,归纳与总结 用钉子把木条分别钉成三角形和四边形,三角形的大小和形状是固定不变的,而四边形的形状会改变。 只要三角形三边的长度确定了,这个三角形的形状和大小就确定,三角形的稳定性就是依据三边对应相等的两个三角形全等.应用 例1:如图: △ABC是一个钢架,AB=AC,AD是连接点A与BC中点D的支架.
求证:△ABD≌△ACDABCD要证明△ABD≌△ACD,就要看这两个三角形的三边是否对应相等.问题2:∠B和∠C相等吗?请说明理由问题3:你还能得到什么其他的结论吗?理由
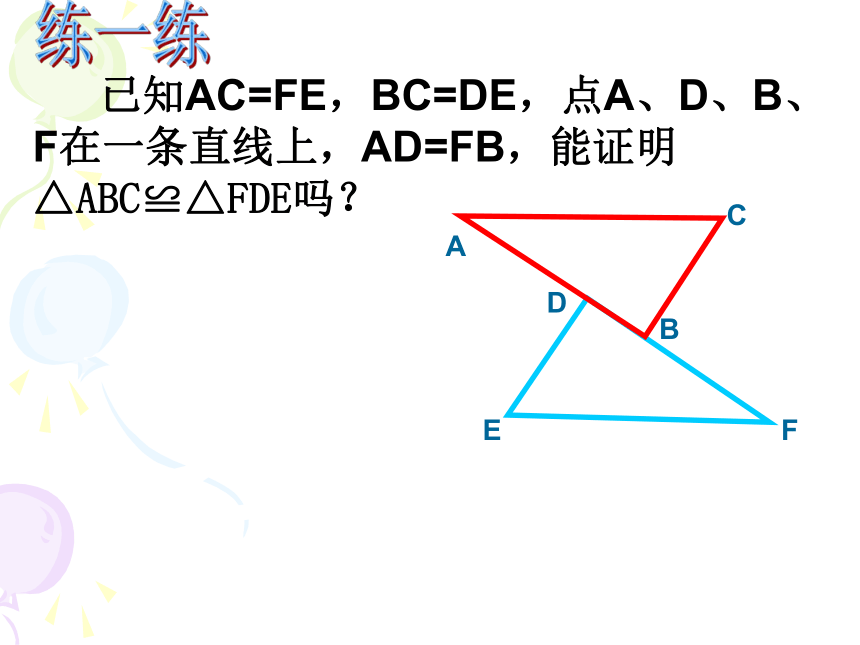
是什么? 已知AC=FE,BC=DE,点A、D、B、F在一条直线上,AD=FB,能证明△ABC≌△FDE吗?练一练 已知AC=FE,BC=DE,点A、D、B、F在一条直线上,AD=FB,能证明△ABC≌△FDE吗?变一变 工人师傅常用角尺平分一个任意角。做法如下:如图:∠AOB是一个任意角,在边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与M,N重合,过角尺顶点C的射线OC便是∠AOB的平分线。为什么?我想我聪明填一填:解: △ABC≌△DCB
理由如下:
AB = CD
AC = BD
=
△ABC ≌(1)如图,AB=CD,AC=BD,△ABC和△DCB是否全等?试说明理由。 BCBC△DCB( S S S )BF=CD请同学们谈谈本节课的收获与体会如图,已知AB=CD,BC=DA。你能说明△ABC与△CDA全等吗?你能说明AB∥CD,AD∥BC吗?为什么? BC解:在△ABC与△CDA中,
∵∴△ABC≌△CDA(SSS)
∴∠BAC=∠DCA,∠ACB=∠CAD(全等三角形对应角相等) D∴AB∥CD,AD∥BC(内错角相等,两直线平行)延伸:如图,AB=AC,BH=CH,D是BC的中点,指出图中全等三角形,它们全等的条件什么?
解:有三组。△ABH≌△ACH△DBH≌△DCH△ABD≌△ACD∴△ABH≌△ACH (SSS)在△ABH和△ACH中在△DBH和△DCH中∴△DBH≌△DCH(SSS) 想一想:如果给出三个条件画三角形时,你能说出有哪几种可能的情况吗?有四种可能:三条边、三个角、两边一角和两角一边。 已知三角形三条边分别是4cm,5cm,7cm,画出这个三形,把所画的三角形分别剪下来,并与同伴比一比,发现什么?
三边对应相等的两个三角形全等,
20006.11.10(1)只给出一个条件(一条边或一个角)画三角形时,画出的三角形一定全等吗?有一条边对应相等的三角形不一定全等有一个角对应相等的三角形不一定全等做一做:(2)给出两个条件画三角形时,有几种可能的情况?每种情况下作出的三角形一定全等吗?不一定全等 只给出一个或两个条件时,都不能保证
所画的三角形一定全等,并且三个内角对
应相等的两个三角形也不一定全等。再探究∵在△ABC和△EFG中AB=EFAC=EGBC=FG∴△ABC≌△EFG(SSS)三边对应相等的两个三角形全等,归纳与总结 用钉子把木条分别钉成三角形和四边形,三角形的大小和形状是固定不变的,而四边形的形状会改变。 只要三角形三边的长度确定了,这个三角形的形状和大小就确定,三角形的稳定性就是依据三边对应相等的两个三角形全等.应用 例1:如图: △ABC是一个钢架,AB=AC,AD是连接点A与BC中点D的支架.
求证:△ABD≌△ACDABCD要证明△ABD≌△ACD,就要看这两个三角形的三边是否对应相等.问题2:∠B和∠C相等吗?请说明理由问题3:你还能得到什么其他的结论吗?理由
是什么? 已知AC=FE,BC=DE,点A、D、B、F在一条直线上,AD=FB,能证明△ABC≌△FDE吗?练一练 已知AC=FE,BC=DE,点A、D、B、F在一条直线上,AD=FB,能证明△ABC≌△FDE吗?变一变 工人师傅常用角尺平分一个任意角。做法如下:如图:∠AOB是一个任意角,在边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与M,N重合,过角尺顶点C的射线OC便是∠AOB的平分线。为什么?我想我聪明填一填:解: △ABC≌△DCB
理由如下:
AB = CD
AC = BD
=
△ABC ≌(1)如图,AB=CD,AC=BD,△ABC和△DCB是否全等?试说明理由。 BCBC△DCB( S S S )BF=CD请同学们谈谈本节课的收获与体会如图,已知AB=CD,BC=DA。你能说明△ABC与△CDA全等吗?你能说明AB∥CD,AD∥BC吗?为什么? BC解:在△ABC与△CDA中,
∵∴△ABC≌△CDA(SSS)
∴∠BAC=∠DCA,∠ACB=∠CAD(全等三角形对应角相等) D∴AB∥CD,AD∥BC(内错角相等,两直线平行)延伸:如图,AB=AC,BH=CH,D是BC的中点,指出图中全等三角形,它们全等的条件什么?
解:有三组。△ABH≌△ACH△DBH≌△DCH△ABD≌△ACD∴△ABH≌△ACH (SSS)在△ABH和△ACH中在△DBH和△DCH中∴△DBH≌△DCH(SSS) 想一想:如果给出三个条件画三角形时,你能说出有哪几种可能的情况吗?有四种可能:三条边、三个角、两边一角和两角一边。 已知三角形三条边分别是4cm,5cm,7cm,画出这个三形,把所画的三角形分别剪下来,并与同伴比一比,发现什么?
三边对应相等的两个三角形全等,
