人教版数学八年级上册 14.3.1提公因式(1)课件(共26张PPT)
文档属性
| 名称 | 人教版数学八年级上册 14.3.1提公因式(1)课件(共26张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 818.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-18 09:46:13 | ||
图片预览






文档简介
(共26张PPT)
14.3.1提公因式法分解因式
回忆
运用前面所学的知识填空:
把下列多项式写 成乘积的形式
都是多项式化为几个整式的积的形式
(1) ma+mb+mc=( )( )
(2) x2 -1 =( )( )
(3) a2 +2ab+b2 =( )2
(1) m(a+b+c)=
(2) (x+1)(x-1)=
(3) (a+b)2 =
ma+mb+mc
x2 -1
a2 +2ab+b2
m a+b+c
x+1 x-1
a+b
探究
观察“回忆”与“探究”,你能发现它们之间的联系与区别吗?
把一个多项式化为几个整式的乘积的形式,像这样的式子变形叫做把这个多项式因式分解,也叫做把这个多项式分解因式。
定义
X2-1 (x+1)(x-1)
因式分解
整式乘法
因式分解和整式乘法是相反方向的变形.
初步应用 巩固新知
从左到右的变形是因式分解的有( )
①
②
③
④
⑤
⑥2
③
⑥
多项式中各项都含有的相同因式,叫做这个多项式的公因式。
相同因式m
这个多项式有什么特点?
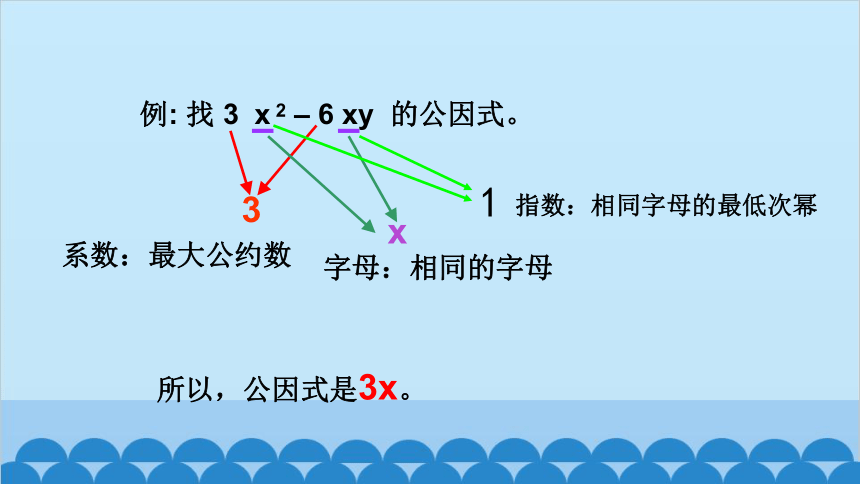
例: 找 3 x 2 – 6 xy 的公因式。
系数:最大公约数
3
字母:相同的字母
x
所以,公因式是3x。
指数:相同字母的最低次幂
1
12a2b3- 8a3b2-16ab4,
系数:找各项系数的最大公约数。
字母:找各项的相同字母。
指数:找各项相同字母的最低次幂的指数。
如何确定公因式?
4ab2
找一找: 下列各多项式的公因式是什么?
(3)
(a)
(a2)
(2(m+n))
(3mn)
(-2xy)
(1) 3x+6y
(2)ab-2ac
(3) a 2 - a 3
(4)4 (m+n) 2 +2(m+n)
(5)9 m 2n-6mn
(6)-6 x 2 y-8 xy 2
如果一个多项式的各项含有公因式,那么
就可以把这个公因式提出来,从而将多项式
化成两个因式乘积 的形式,这种分解因式的
方法叫做提公因式法。
( a+b+c )
ma+ mb +mc
m
=
用提公因式法分解因式:
(1) -2x3+6x2-2x
(2) -3an+2+2an+1-7an
1.把下列多项式因式分解:
(1) 4ab-2a2b; (2) -3ab+6abx-9aby
(3) - 24m2x+16n2x; (4) anb2-2anb.
2ab(2-a)
-3ab(1-2x+3y)
-8x(3m2-2n2)
anb(b-2)
当堂练习
2 把下列各式分解因式
(1) 2a(b+c)-3(b+c)
(2) 2a(b-c)-3(c-b)
(3) 6a(b-c)2-3(c-b)3
(4) (2x+3y)(3x-2y)-5x(2x+3y)
3、把下列各式分解因式
2a(y-x)-3b(x-y)
(2) p(a2+b2)-q(a2+b2)
(3) 2(a-3)2 -(a-3)
2.先分解因式,再求值:
4a2(x+7)-3(x+7),其中a=-5,x=3.
1.计算21×3.14+62×3.14+17×3.14
2、确定公因式的方法:
小结
3、提公因式法分解因式步骤(分两步):
1、什么叫因式分解?
(1)定系数 (2)定字母 (3)定指数
第一步,找出公因式;
第二步,提取公因式.
4、提公因式法分解因式应注意的问题:
(1)公因式要提尽;
(2)小心漏掉1;
(3)提出负号时,要注意变号.
1. 分解因式:
8m2n+2mn;
(2)12xyz-9x2y2;
(3)-12a2b+24ab2
(4)2a(y-z)-3b(z-y);
(5)p(a2+b2)-q(a2+b2).
当堂检测
1、分解因式:
练习.分解因式:
14.3.1提公因式法分解因式
回忆
运用前面所学的知识填空:
把下列多项式写 成乘积的形式
都是多项式化为几个整式的积的形式
(1) ma+mb+mc=( )( )
(2) x2 -1 =( )( )
(3) a2 +2ab+b2 =( )2
(1) m(a+b+c)=
(2) (x+1)(x-1)=
(3) (a+b)2 =
ma+mb+mc
x2 -1
a2 +2ab+b2
m a+b+c
x+1 x-1
a+b
探究
观察“回忆”与“探究”,你能发现它们之间的联系与区别吗?
把一个多项式化为几个整式的乘积的形式,像这样的式子变形叫做把这个多项式因式分解,也叫做把这个多项式分解因式。
定义
X2-1 (x+1)(x-1)
因式分解
整式乘法
因式分解和整式乘法是相反方向的变形.
初步应用 巩固新知
从左到右的变形是因式分解的有( )
①
②
③
④
⑤
⑥2
③
⑥
多项式中各项都含有的相同因式,叫做这个多项式的公因式。
相同因式m
这个多项式有什么特点?
例: 找 3 x 2 – 6 xy 的公因式。
系数:最大公约数
3
字母:相同的字母
x
所以,公因式是3x。
指数:相同字母的最低次幂
1
12a2b3- 8a3b2-16ab4,
系数:找各项系数的最大公约数。
字母:找各项的相同字母。
指数:找各项相同字母的最低次幂的指数。
如何确定公因式?
4ab2
找一找: 下列各多项式的公因式是什么?
(3)
(a)
(a2)
(2(m+n))
(3mn)
(-2xy)
(1) 3x+6y
(2)ab-2ac
(3) a 2 - a 3
(4)4 (m+n) 2 +2(m+n)
(5)9 m 2n-6mn
(6)-6 x 2 y-8 xy 2
如果一个多项式的各项含有公因式,那么
就可以把这个公因式提出来,从而将多项式
化成两个因式乘积 的形式,这种分解因式的
方法叫做提公因式法。
( a+b+c )
ma+ mb +mc
m
=
用提公因式法分解因式:
(1) -2x3+6x2-2x
(2) -3an+2+2an+1-7an
1.把下列多项式因式分解:
(1) 4ab-2a2b; (2) -3ab+6abx-9aby
(3) - 24m2x+16n2x; (4) anb2-2anb.
2ab(2-a)
-3ab(1-2x+3y)
-8x(3m2-2n2)
anb(b-2)
当堂练习
2 把下列各式分解因式
(1) 2a(b+c)-3(b+c)
(2) 2a(b-c)-3(c-b)
(3) 6a(b-c)2-3(c-b)3
(4) (2x+3y)(3x-2y)-5x(2x+3y)
3、把下列各式分解因式
2a(y-x)-3b(x-y)
(2) p(a2+b2)-q(a2+b2)
(3) 2(a-3)2 -(a-3)
2.先分解因式,再求值:
4a2(x+7)-3(x+7),其中a=-5,x=3.
1.计算21×3.14+62×3.14+17×3.14
2、确定公因式的方法:
小结
3、提公因式法分解因式步骤(分两步):
1、什么叫因式分解?
(1)定系数 (2)定字母 (3)定指数
第一步,找出公因式;
第二步,提取公因式.
4、提公因式法分解因式应注意的问题:
(1)公因式要提尽;
(2)小心漏掉1;
(3)提出负号时,要注意变号.
1. 分解因式:
8m2n+2mn;
(2)12xyz-9x2y2;
(3)-12a2b+24ab2
(4)2a(y-z)-3b(z-y);
(5)p(a2+b2)-q(a2+b2).
当堂检测
1、分解因式:
练习.分解因式:
