13-2 三角形全等的条件(复习2)[上学期]
文档属性
| 名称 | 13-2 三角形全等的条件(复习2)[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 293.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-11-27 00:00:00 | ||
图片预览

文档简介
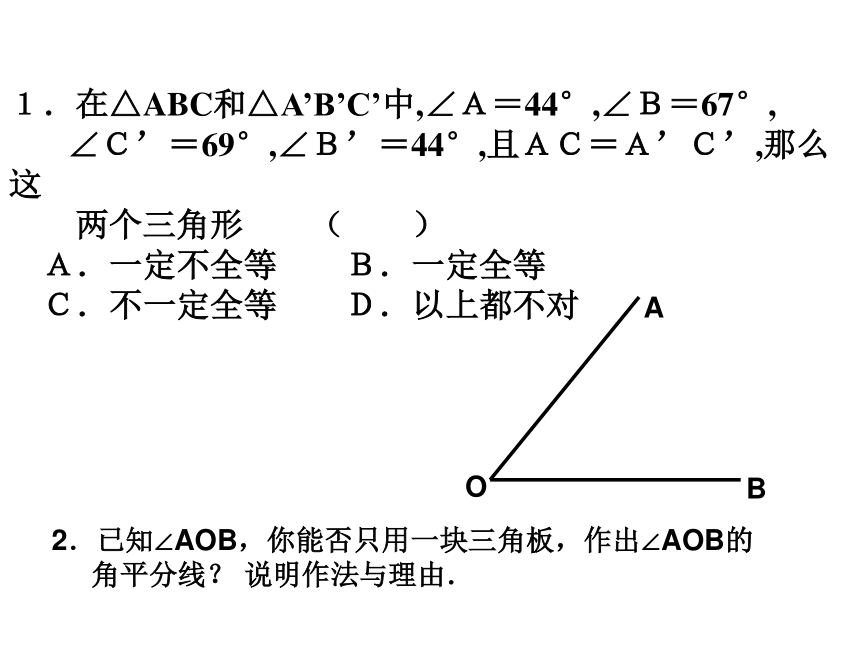
课件15张PPT。13-2 三角形全等的条件(复习)1.在△ABC和△A’B’C’中,∠A=44°,∠B=67°,
∠C’=69°,∠B’=44°,且AC=A’C’,那么这
两个三角形 ( )
A.一定不全等 B.一定全等
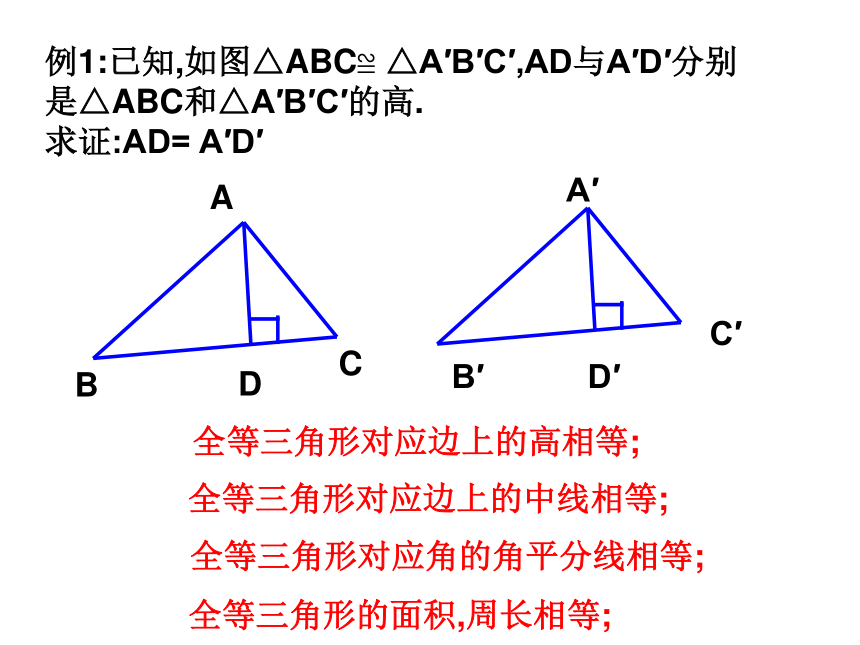
C.不一定全等 D.以上都不对例1:已知,如图△ABC≌ △A′B′C′,AD与A′D′分别是△ABC和△A′B′C′的高.
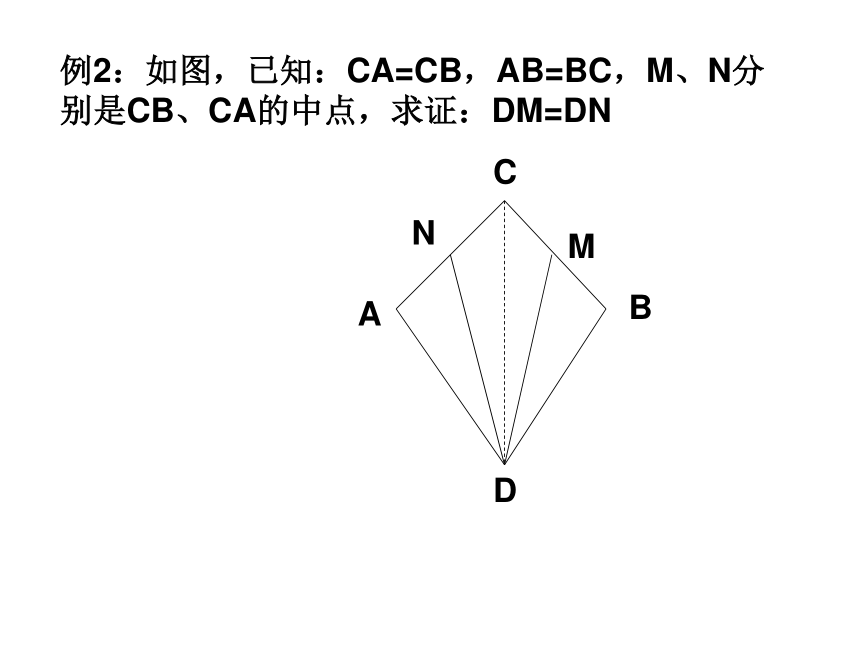
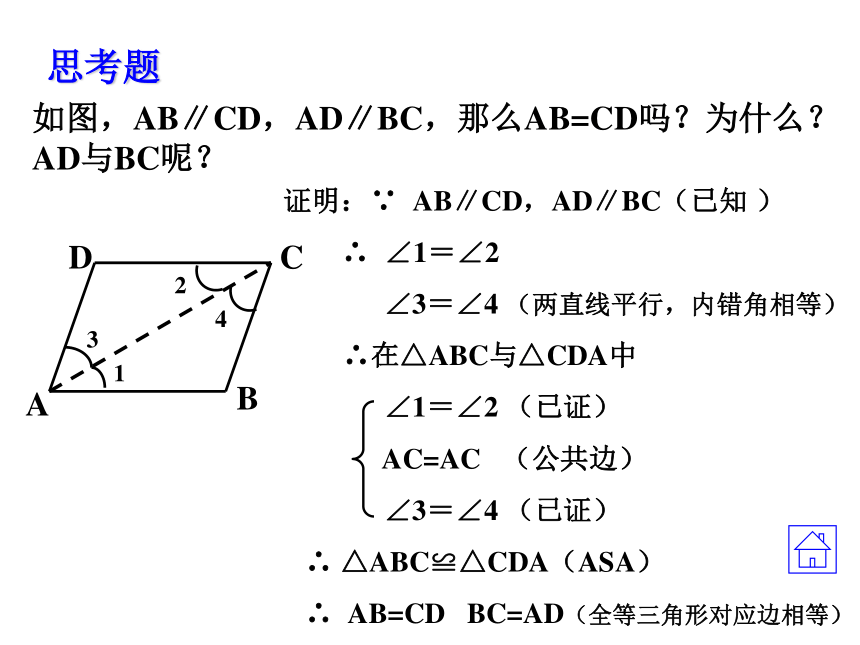
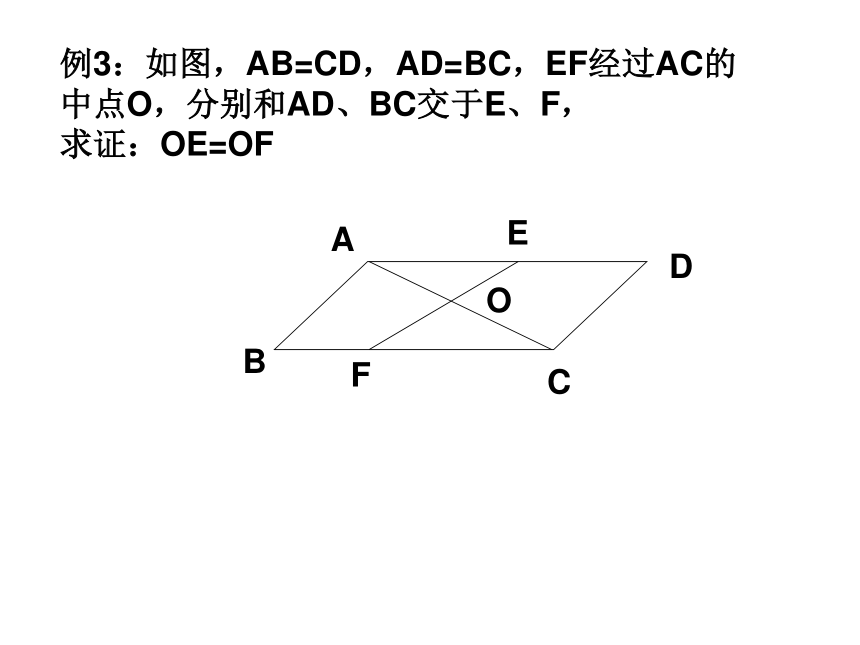
求证:AD= A′D′ABDCA′B′C′D′全等三角形对应边上的高相等;全等三角形对应边上的中线相等;全等三角形对应角的角平分线相等;全等三角形的面积,周长相等;例2:如图,已知:CA=CB,AB=BC,M、N分别是CB、CA的中点,求证:DM=DNABCDMN如图,AB∥CD,AD∥BC,那么AB=CD吗?为什么?AD与BC呢?思考题例3:如图,AB=CD,AD=BC,EF经过AC的中点O,分别和AD、BC交于E、F,
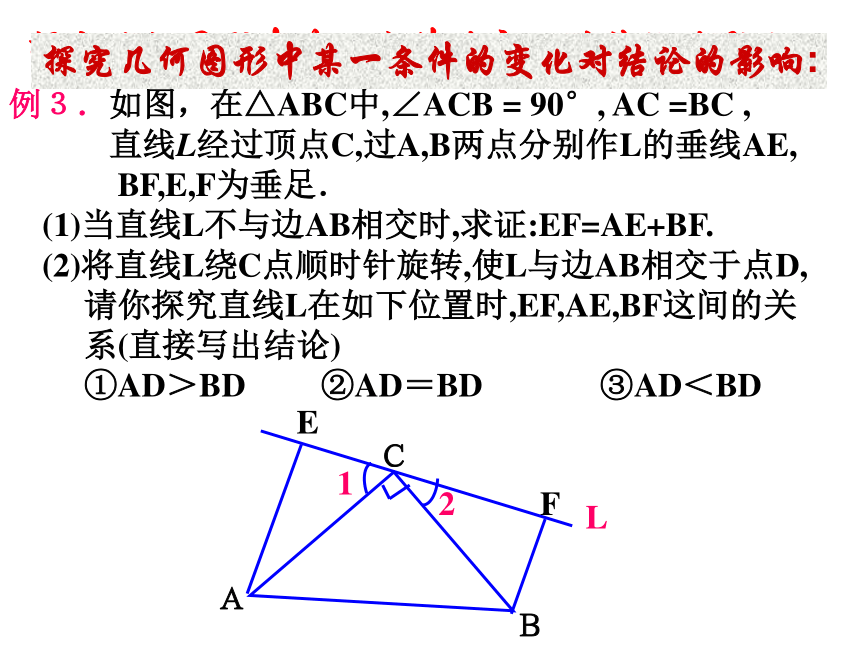
求证:OE=OF探究几何图形中某一条件的变化对结论的影响:探究几何图形中某一条件的变化对结论的影响:例3.如图,在△ABC中,∠ACB = 90°, AC =BC ,
直线L经过顶点C,过A,B两点分别作L的垂线AE,
BF,E,F为垂足.
(1)当直线L不与边AB相交时,求证:EF=AE+BF.
(2)将直线L绕C点顺时针旋转,使L与边AB相交于点D,
请你探究直线L在如下位置时,EF,AE,BF这间的关
系(直接写出结论)
①AD>BD ②AD=BD ③AD<BD探究几何图形中某一条件的变化对结论的影响:探究几何图形中某一条件的变化对结论的影响:例3.如图,在△ABC中,∠ACB = 90°, AC =BC ,
直线L经过顶点C,过A,B两点分别作L的垂线AE,
BF,E,F为垂足.
(1)当直线L不与边AB相交时,求证:EF=AE+BF.
(2)将直线L绕C点顺时针旋转,使L与边AB相交于点D,
请你探究直线L在如下位置时,EF,AE,BF这间的关
系(直接写出结论)
①AD>BD ②AD=BD ③AD<BD探究几何图形中某一条件的变化对结论的影响:探究几何图形中某一条件的变化对结论的影响:例3.如图,在△ABC中,∠ACB = 90°, AC =BC ,
直线L经过顶点C,过A,B两点分别作L的垂线AE,
BF,E,F为垂足.
(1)当直线L不与边AB相交时,求证:EF=AE+BF.
(2)将直线L绕C点顺时针旋转,使L与边AB相交于点D,
请你探究直线L在如下位置时,EF,AE,BF这间的关
系(直接写出结论)
①AD>BD ②AD=BD ③AD<BD探究几何图形中某一条件的变化对结论的影响:特别提示:
添加辅助线应以不破坏已知条件为前提.添辅助线构造全等三角形解题例6.如图,在△ABC中,AB=12,AC=8,AD是BC边上
的中线,求AD的取值范围.特别提示:
把三角形的一边的中线加倍延长,把分散条件集中
到同一个三角形中是解决中线问题的基本规律.添辅助线构造全等三角形解题5.若AD是Rt△ABC的斜边上的中线,那么△ABD≌△ADC吗?
为什么?
小明是这样想的:
△ABD≌△ADC 这是因为:
△ABC为直角三角形. △ABD≌△ADC 小明思考得对吗? 拓展与延伸下图是一个等边三角形,你能把它分成两个全等三角形吗?你能把它分成三个全等三角形吗?四个呢?经过本节课的学习,你有哪些收获?小结
∠C’=69°,∠B’=44°,且AC=A’C’,那么这
两个三角形 ( )
A.一定不全等 B.一定全等
C.不一定全等 D.以上都不对例1:已知,如图△ABC≌ △A′B′C′,AD与A′D′分别是△ABC和△A′B′C′的高.
求证:AD= A′D′ABDCA′B′C′D′全等三角形对应边上的高相等;全等三角形对应边上的中线相等;全等三角形对应角的角平分线相等;全等三角形的面积,周长相等;例2:如图,已知:CA=CB,AB=BC,M、N分别是CB、CA的中点,求证:DM=DNABCDMN如图,AB∥CD,AD∥BC,那么AB=CD吗?为什么?AD与BC呢?思考题例3:如图,AB=CD,AD=BC,EF经过AC的中点O,分别和AD、BC交于E、F,
求证:OE=OF探究几何图形中某一条件的变化对结论的影响:探究几何图形中某一条件的变化对结论的影响:例3.如图,在△ABC中,∠ACB = 90°, AC =BC ,
直线L经过顶点C,过A,B两点分别作L的垂线AE,
BF,E,F为垂足.
(1)当直线L不与边AB相交时,求证:EF=AE+BF.
(2)将直线L绕C点顺时针旋转,使L与边AB相交于点D,
请你探究直线L在如下位置时,EF,AE,BF这间的关
系(直接写出结论)
①AD>BD ②AD=BD ③AD<BD探究几何图形中某一条件的变化对结论的影响:探究几何图形中某一条件的变化对结论的影响:例3.如图,在△ABC中,∠ACB = 90°, AC =BC ,
直线L经过顶点C,过A,B两点分别作L的垂线AE,
BF,E,F为垂足.
(1)当直线L不与边AB相交时,求证:EF=AE+BF.
(2)将直线L绕C点顺时针旋转,使L与边AB相交于点D,
请你探究直线L在如下位置时,EF,AE,BF这间的关
系(直接写出结论)
①AD>BD ②AD=BD ③AD<BD探究几何图形中某一条件的变化对结论的影响:探究几何图形中某一条件的变化对结论的影响:例3.如图,在△ABC中,∠ACB = 90°, AC =BC ,
直线L经过顶点C,过A,B两点分别作L的垂线AE,
BF,E,F为垂足.
(1)当直线L不与边AB相交时,求证:EF=AE+BF.
(2)将直线L绕C点顺时针旋转,使L与边AB相交于点D,
请你探究直线L在如下位置时,EF,AE,BF这间的关
系(直接写出结论)
①AD>BD ②AD=BD ③AD<BD探究几何图形中某一条件的变化对结论的影响:特别提示:
添加辅助线应以不破坏已知条件为前提.添辅助线构造全等三角形解题例6.如图,在△ABC中,AB=12,AC=8,AD是BC边上
的中线,求AD的取值范围.特别提示:
把三角形的一边的中线加倍延长,把分散条件集中
到同一个三角形中是解决中线问题的基本规律.添辅助线构造全等三角形解题5.若AD是Rt△ABC的斜边上的中线,那么△ABD≌△ADC吗?
为什么?
小明是这样想的:
△ABD≌△ADC 这是因为:
△ABC为直角三角形. △ABD≌△ADC 小明思考得对吗? 拓展与延伸下图是一个等边三角形,你能把它分成两个全等三角形吗?你能把它分成三个全等三角形吗?四个呢?经过本节课的学习,你有哪些收获?小结
