4.4对数函数及其性质教案-2022-2023学年高一上学期数学人教A版(2019)必修第一册(无答案)
文档属性
| 名称 | 4.4对数函数及其性质教案-2022-2023学年高一上学期数学人教A版(2019)必修第一册(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 803.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-18 10:39:46 | ||
图片预览




文档简介
数学学生讲义
学生姓名: 年级:高一年级 科目:数学 学科教师:
课题 对数函数及其性质
授课类型 基础知识回顾 经典例题再现 巩固提升
教学目标 1.理解对数函数的概念,体会对数函数是一类很重要的函数模型; 2.探索对数函数的单调性与特殊点,掌握对数函数的性质,会进行同底对数和不同底对数大小的比较; 3.了解反函数的概念,知道指数函数与对数函数互为反函数.
教学重难点 探索对数函数的单调性与特殊点,掌握对数函数的性质。
授课日期及时段
教学内容
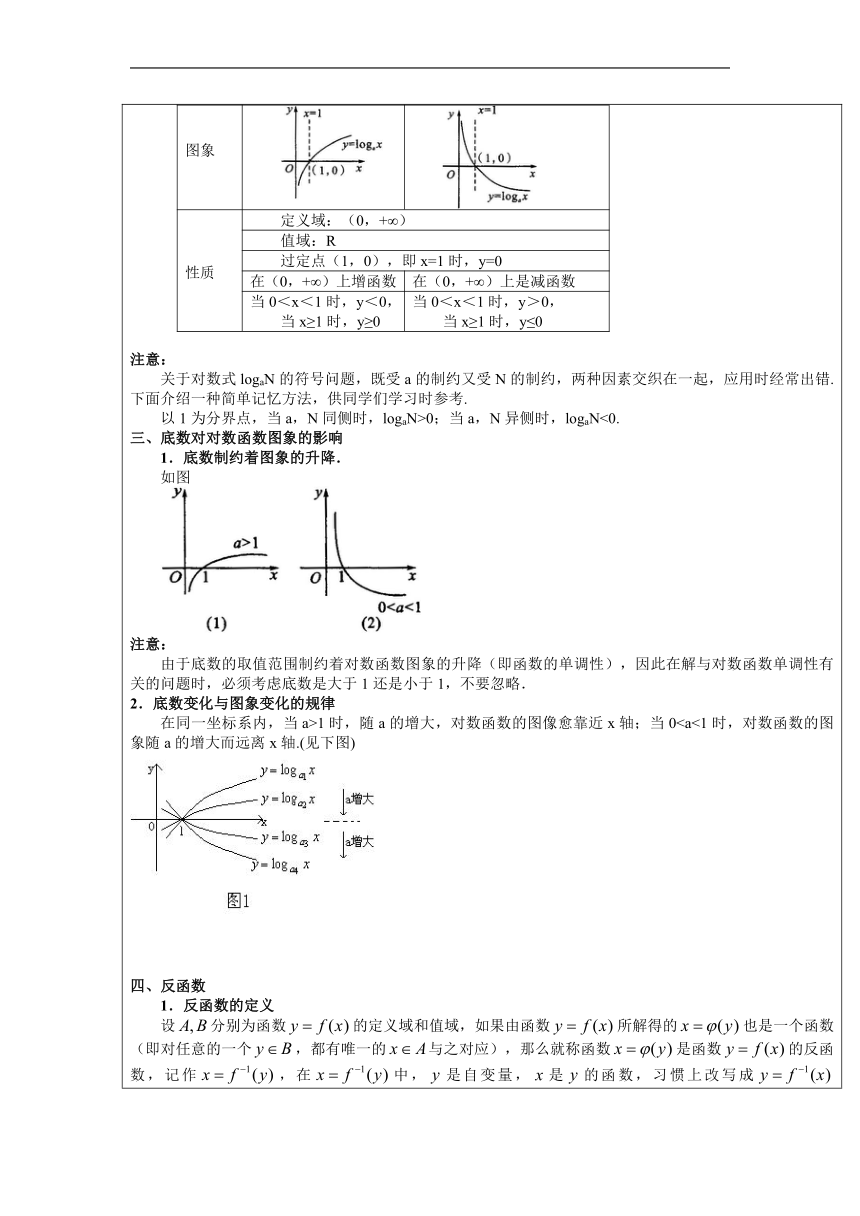
一、对数函数的概念 1.函数y=logax(a>0,a≠1)叫做对数函数.其中是自变量,函数的定义域是,值域为. 2.判断一个函数是对数函数是形如的形式,即必须满足以下条件: (1)系数为1; (2)底数为大于0且不等于1的常数; (3)对数的真数仅有自变量. 注意: (1)只有形如y=logax(a>0,a≠1)的函数才叫做对数函数,像等函数,它们是由对数函数变化得到的,都不是对数函数。 (2)求对数函数的定义域时应注意:①对数函数的真数要求大于零,底数大于零且不等于1;②对含有字母的式子要注意分类讨论。 二、对数函数的图象与性质 a>10<a<1 图象 性质定义域:(0,+∞)值域:R过定点(1,0),即x=1时,y=0在(0,+∞)上增函数在(0,+∞)上是减函数当0<x<1时,y<0, 当x≥1时,y≥0当0<x<1时,y>0, 当x≥1时,y≤0
注意: 关于对数式logaN的符号问题,既受a的制约又受N的制约,两种因素交织在一起,应用时经常出错.下面介绍一种简单记忆方法,供同学们学习时参考. 以1为分界点,当a,N同侧时,logaN>0;当a,N异侧时,logaN<0. 三、底数对对数函数图象的影响 1.底数制约着图象的升降. 如图 注意: 由于底数的取值范围制约着对数函数图象的升降(即函数的单调性),因此在解与对数函数单调性有关的问题时,必须考虑底数是大于1还是小于1,不要忽略. 2.底数变化与图象变化的规律 在同一坐标系内,当a>1时,随a的增大,对数函数的图像愈靠近x轴;当0
学生姓名: 年级:高一年级 科目:数学 学科教师:
课题 对数函数及其性质
授课类型 基础知识回顾 经典例题再现 巩固提升
教学目标 1.理解对数函数的概念,体会对数函数是一类很重要的函数模型; 2.探索对数函数的单调性与特殊点,掌握对数函数的性质,会进行同底对数和不同底对数大小的比较; 3.了解反函数的概念,知道指数函数与对数函数互为反函数.
教学重难点 探索对数函数的单调性与特殊点,掌握对数函数的性质。
授课日期及时段
教学内容
一、对数函数的概念 1.函数y=logax(a>0,a≠1)叫做对数函数.其中是自变量,函数的定义域是,值域为. 2.判断一个函数是对数函数是形如的形式,即必须满足以下条件: (1)系数为1; (2)底数为大于0且不等于1的常数; (3)对数的真数仅有自变量. 注意: (1)只有形如y=logax(a>0,a≠1)的函数才叫做对数函数,像等函数,它们是由对数函数变化得到的,都不是对数函数。 (2)求对数函数的定义域时应注意:①对数函数的真数要求大于零,底数大于零且不等于1;②对含有字母的式子要注意分类讨论。 二、对数函数的图象与性质 a>10<a<1 图象 性质定义域:(0,+∞)值域:R过定点(1,0),即x=1时,y=0在(0,+∞)上增函数在(0,+∞)上是减函数当0<x<1时,y<0, 当x≥1时,y≥0当0<x<1时,y>0, 当x≥1时,y≤0
注意: 关于对数式logaN的符号问题,既受a的制约又受N的制约,两种因素交织在一起,应用时经常出错.下面介绍一种简单记忆方法,供同学们学习时参考. 以1为分界点,当a,N同侧时,logaN>0;当a,N异侧时,logaN<0. 三、底数对对数函数图象的影响 1.底数制约着图象的升降. 如图 注意: 由于底数的取值范围制约着对数函数图象的升降(即函数的单调性),因此在解与对数函数单调性有关的问题时,必须考虑底数是大于1还是小于1,不要忽略. 2.底数变化与图象变化的规律 在同一坐标系内,当a>1时,随a的增大,对数函数的图像愈靠近x轴;当0
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
