北师大版八年级数学上册试题 第四章 一次函数 复习卷 (含答案)
文档属性
| 名称 | 北师大版八年级数学上册试题 第四章 一次函数 复习卷 (含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 255.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-18 09:52:46 | ||
图片预览

文档简介
第四章 《一次函数》复习卷
一、选择题。
1.下列等式中,是的函数有( )个.
A.1 B.2 C.3 D.4
2.函数y=自变量x的取值范围是( )
A.全体实数 B.x≠0 C.x<2 D.x≠2
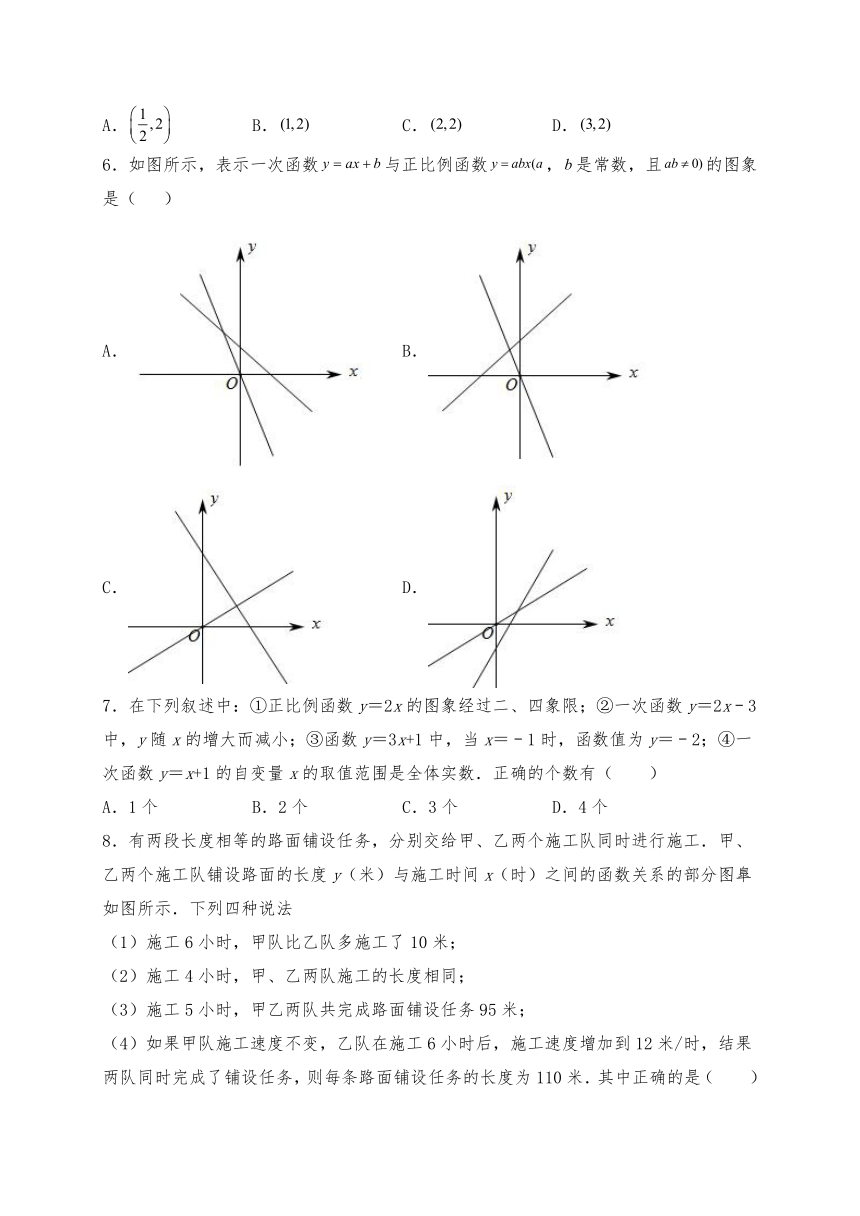
3.小苏和小林在如图所示的跑道上进行4×50米折返跑.在整个过程中,跑步者距起跑线的距离y(单位:m)与跑步时间t(单位:s)的对应关系如下图所示.下列叙述正确的是( )
A.两人从起跑线同时出发,同时到达终点
B.小苏跑全程的平均速度大于小林跑全程的平均速度
C.小苏在跑最后100m的过程中,与小林相遇2次
D.小苏前15s跑过的路程小于小林前15s跑过的路程
4.已知正比例函数y=kx,当x=2时,y=6,则下列各点在该函数图象上的是( )
A.(﹣1,﹣2) B.(﹣1,3) C.(1,3) D.(3,1)
5.如图,在平面直角坐标系中,一次函数经过点,与x轴、y轴分别交于点A和点B,在区域内(不含边界)的点有( )
A. B. C. D.
6.如图所示,表示一次函数与正比例函数,是常数,且的图象是( )
A. B.
C. D.
7.在下列叙述中:①正比例函数y=2x的图象经过二、四象限;②一次函数y=2x﹣3中,y随x的增大而减小;③函数y=3x+1中,当x=﹣1时,函数值为y=﹣2;④一次函数y=x+1的自变量x的取值范围是全体实数.正确的个数有( )
A.1个 B.2个 C.3个 D.4个
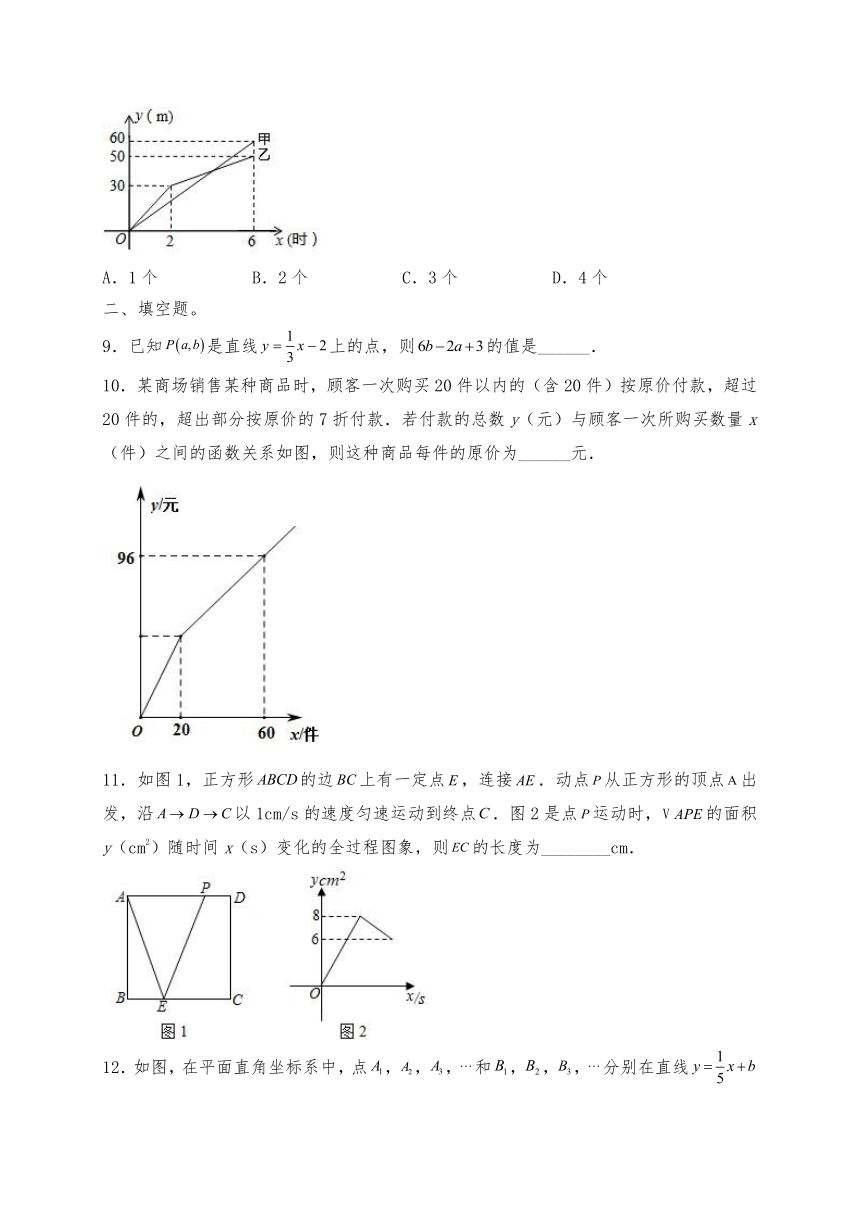
8.有两段长度相等的路面铺设任务,分别交给甲、乙两个施工队同时进行施工.甲、乙两个施工队铺设路面的长度y(米)与施工时间x(时)之间的函数关系的部分图臯如图所示.下列四种说法
(1)施工6小时,甲队比乙队多施工了10米;
(2)施工4小时,甲、乙两队施工的长度相同;
(3)施工5小时,甲乙两队共完成路面铺设任务95米;
(4)如果甲队施工速度不变,乙队在施工6小时后,施工速度增加到12米/时,结果两队同时完成了铺设任务,则每条路面铺设任务的长度为110米.其中正确的是( )
A.1个 B.2个 C.3个 D.4个
二、填空题。
9.已知是直线上的点,则的值是______.
10.某商场销售某种商品时,顾客一次购买20件以内的(含20件)按原价付款,超过20件的,超出部分按原价的7折付款.若付款的总数y(元)与顾客一次所购买数量x(件)之间的函数关系如图,则这种商品每件的原价为______元.
11.如图1,正方形的边上有一定点,连接.动点从正方形的顶点出发,沿以1cm/s的速度匀速运动到终点.图2是点运动时,的面积y(cm2)随时间x(s)变化的全过程图象,则的长度为________cm.
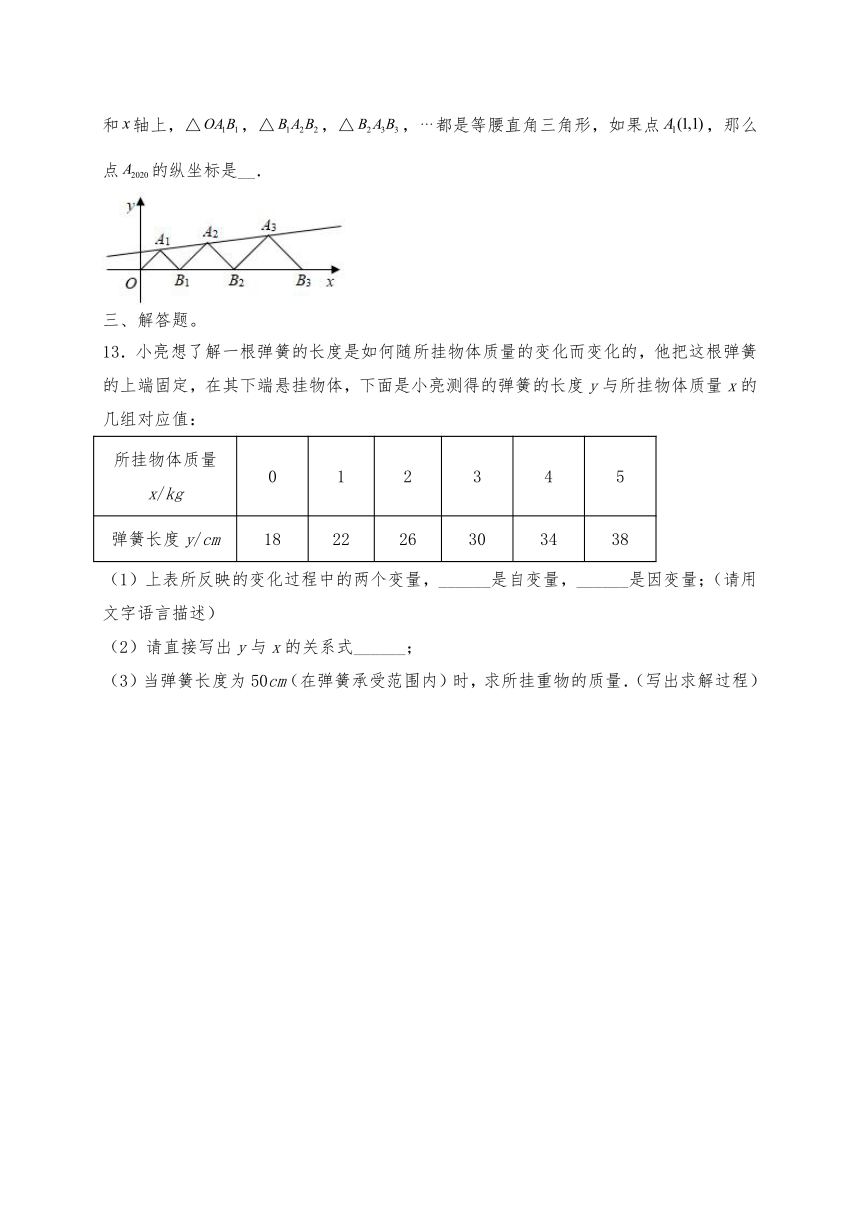
12.如图,在平面直角坐标系中,点,,,和,,,分别在直线和轴上,△,△,△,都是等腰直角三角形,如果点,那么点的纵坐标是__.
三、解答题。
13.小亮想了解一根弹簧的长度是如何随所挂物体质量的变化而变化的,他把这根弹簧的上端固定,在其下端悬挂物体,下面是小亮测得的弹簧的长度y与所挂物体质量x的几组对应值:
所挂物体质量x/kg 0 1 2 3 4 5
弹簧长度y/cm 18 22 26 30 34 38
(1)上表所反映的变化过程中的两个变量,______是自变量,______是因变量;(请用文字语言描述)
(2)请直接写出y与x的关系式______;
(3)当弹簧长度为50cm(在弹簧承受范围内)时,求所挂重物的质量.(写出求解过程)
14.如图,在平面直角坐标系中,一次函数的图象经过点,且与正比例函数的图象交于点
(1)求一次函数的解析式;
(2)若直线与轴交于点,若连接后,请直接写出的面积是______.
15.“环境就是民生,青山就是美丽,蓝天也是幸福”,为建立整洁舒适的居住环境,某小区物业打算购买一批垃圾桶.
方案:买分类垃圾桶,需要费用元,以后每月垃圾处理费用元;
方案:买不分类垃圾桶,需要费用元,以后每月的垃圾处理费用为元.
设交费时间为个月,购买费和垃圾处理费共元.
分别写出两种方案中与之间的函数表达式:
方案:____________________;方案:____________________.
在同一平面直角坐标系中,画出、的图象;
请说明中,和的实际意义?
在垃圾桶的使用寿命相同的情况下,那种方案更省钱?
答案
一、选择题。
C.D.D.C.B.A.B.D.
二、填空题。
9.-1.
10.2
11.3.
12..
三、解答题。
13.
解:(1)上表反映了弹簧长度与所挂物体质量之间的关系;其中所挂物体质量是自变量,弹簧长度是因变量;
故答案为:所挂物体质量,弹簧长度;
(2)由表格可得:当所挂物体重量为1千克时,弹簧长4厘米;当不挂重物时,弹簧长18厘米,
则y与x的关系式为:y=4x+18;
故答案为:y=4x+18;
(3)当弹簧长度为50cm(在弹簧承受范围内)时,
50=4x+18,
解得x=8,
答:所挂重物的质量为8kg.
14.
解:(1)把点代入得,,
∴,
∴,
把,代入得,
解得:,
∴一次函数的解析式为:;
(2)连接OC,
∵一次函数解析式为,
令时,,
∴,
∵,,
∴;
故答案是4.
15.
解:(1)由题意,得y1=250x+3000,y2=500x+1000;
故答案为:250x+3000, 500x+1000;
(2)如图所示:
(3)中,的实际意义是每月垃圾处理费用,的实际意义买分类垃圾桶需要的费用;
(4)由图象可知:当使用时间少于8个月时,直线y2落在直线y1的下方,y2y1,即方案1省钱.当使用时间正好8个月时,两种方案一样
一、选择题。
1.下列等式中,是的函数有( )个.
A.1 B.2 C.3 D.4
2.函数y=自变量x的取值范围是( )
A.全体实数 B.x≠0 C.x<2 D.x≠2
3.小苏和小林在如图所示的跑道上进行4×50米折返跑.在整个过程中,跑步者距起跑线的距离y(单位:m)与跑步时间t(单位:s)的对应关系如下图所示.下列叙述正确的是( )
A.两人从起跑线同时出发,同时到达终点
B.小苏跑全程的平均速度大于小林跑全程的平均速度
C.小苏在跑最后100m的过程中,与小林相遇2次
D.小苏前15s跑过的路程小于小林前15s跑过的路程
4.已知正比例函数y=kx,当x=2时,y=6,则下列各点在该函数图象上的是( )
A.(﹣1,﹣2) B.(﹣1,3) C.(1,3) D.(3,1)
5.如图,在平面直角坐标系中,一次函数经过点,与x轴、y轴分别交于点A和点B,在区域内(不含边界)的点有( )
A. B. C. D.
6.如图所示,表示一次函数与正比例函数,是常数,且的图象是( )
A. B.
C. D.
7.在下列叙述中:①正比例函数y=2x的图象经过二、四象限;②一次函数y=2x﹣3中,y随x的增大而减小;③函数y=3x+1中,当x=﹣1时,函数值为y=﹣2;④一次函数y=x+1的自变量x的取值范围是全体实数.正确的个数有( )
A.1个 B.2个 C.3个 D.4个
8.有两段长度相等的路面铺设任务,分别交给甲、乙两个施工队同时进行施工.甲、乙两个施工队铺设路面的长度y(米)与施工时间x(时)之间的函数关系的部分图臯如图所示.下列四种说法
(1)施工6小时,甲队比乙队多施工了10米;
(2)施工4小时,甲、乙两队施工的长度相同;
(3)施工5小时,甲乙两队共完成路面铺设任务95米;
(4)如果甲队施工速度不变,乙队在施工6小时后,施工速度增加到12米/时,结果两队同时完成了铺设任务,则每条路面铺设任务的长度为110米.其中正确的是( )
A.1个 B.2个 C.3个 D.4个
二、填空题。
9.已知是直线上的点,则的值是______.
10.某商场销售某种商品时,顾客一次购买20件以内的(含20件)按原价付款,超过20件的,超出部分按原价的7折付款.若付款的总数y(元)与顾客一次所购买数量x(件)之间的函数关系如图,则这种商品每件的原价为______元.
11.如图1,正方形的边上有一定点,连接.动点从正方形的顶点出发,沿以1cm/s的速度匀速运动到终点.图2是点运动时,的面积y(cm2)随时间x(s)变化的全过程图象,则的长度为________cm.
12.如图,在平面直角坐标系中,点,,,和,,,分别在直线和轴上,△,△,△,都是等腰直角三角形,如果点,那么点的纵坐标是__.
三、解答题。
13.小亮想了解一根弹簧的长度是如何随所挂物体质量的变化而变化的,他把这根弹簧的上端固定,在其下端悬挂物体,下面是小亮测得的弹簧的长度y与所挂物体质量x的几组对应值:
所挂物体质量x/kg 0 1 2 3 4 5
弹簧长度y/cm 18 22 26 30 34 38
(1)上表所反映的变化过程中的两个变量,______是自变量,______是因变量;(请用文字语言描述)
(2)请直接写出y与x的关系式______;
(3)当弹簧长度为50cm(在弹簧承受范围内)时,求所挂重物的质量.(写出求解过程)
14.如图,在平面直角坐标系中,一次函数的图象经过点,且与正比例函数的图象交于点
(1)求一次函数的解析式;
(2)若直线与轴交于点,若连接后,请直接写出的面积是______.
15.“环境就是民生,青山就是美丽,蓝天也是幸福”,为建立整洁舒适的居住环境,某小区物业打算购买一批垃圾桶.
方案:买分类垃圾桶,需要费用元,以后每月垃圾处理费用元;
方案:买不分类垃圾桶,需要费用元,以后每月的垃圾处理费用为元.
设交费时间为个月,购买费和垃圾处理费共元.
分别写出两种方案中与之间的函数表达式:
方案:____________________;方案:____________________.
在同一平面直角坐标系中,画出、的图象;
请说明中,和的实际意义?
在垃圾桶的使用寿命相同的情况下,那种方案更省钱?
答案
一、选择题。
C.D.D.C.B.A.B.D.
二、填空题。
9.-1.
10.2
11.3.
12..
三、解答题。
13.
解:(1)上表反映了弹簧长度与所挂物体质量之间的关系;其中所挂物体质量是自变量,弹簧长度是因变量;
故答案为:所挂物体质量,弹簧长度;
(2)由表格可得:当所挂物体重量为1千克时,弹簧长4厘米;当不挂重物时,弹簧长18厘米,
则y与x的关系式为:y=4x+18;
故答案为:y=4x+18;
(3)当弹簧长度为50cm(在弹簧承受范围内)时,
50=4x+18,
解得x=8,
答:所挂重物的质量为8kg.
14.
解:(1)把点代入得,,
∴,
∴,
把,代入得,
解得:,
∴一次函数的解析式为:;
(2)连接OC,
∵一次函数解析式为,
令时,,
∴,
∵,,
∴;
故答案是4.
15.
解:(1)由题意,得y1=250x+3000,y2=500x+1000;
故答案为:250x+3000, 500x+1000;
(2)如图所示:
(3)中,的实际意义是每月垃圾处理费用,的实际意义买分类垃圾桶需要的费用;
(4)由图象可知:当使用时间少于8个月时,直线y2落在直线y1的下方,y2
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
