八年级数学上册试题 第五章 《二元一次方程组》单元测试卷 -北师大版(含答案)
文档属性
| 名称 | 八年级数学上册试题 第五章 《二元一次方程组》单元测试卷 -北师大版(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 440.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-18 10:13:08 | ||
图片预览


文档简介
第五章 《二元一次方程组》单元测试卷
一、选择题:本题共12个小题,每小题3分,共36分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.我国古代数学名著《孙子算经》中记载了一道题,大意是:有100匹马恰好拉了100片瓦,已知1匹大马能拉3片瓦,3匹小马能拉1片瓦,问有多少匹大马、多少匹小马?若设大马有x匹,小马有y匹,那么可列方程组为( )
A. B.
C. D.
2.某商场新购进一种服装,每套售价1000元,若将裤子降价10%,上衣涨价5%,调价后这套服装的单价比原来提高了2%,则调价前上衣的单价是( )
A.200元 B.480元 C.600元 D.800元
3.大课间,12人跳绳队为尊重每个队员的意愿,准备把队员分成跳大绳组或跳小绳组,大绳组3人一组,小绳组2人一组,在全队同学能同时参加活动且符合小组规定人数的前提下,则不同的分组方法有( )
A.1种 B.2种 C.3种 D.4种
4.已知关于,的方程组与有相同的解,则,的值为( )
A. B. C. D.
5.已知关于,的方程组,给出下列说法:①当时,方程组的解也是方程的一个解;②当时,;③不论取什么实数,的值始终不变;④若,则以上四种说法中正确的有( )个
A.1 B.2 C.3 D.4
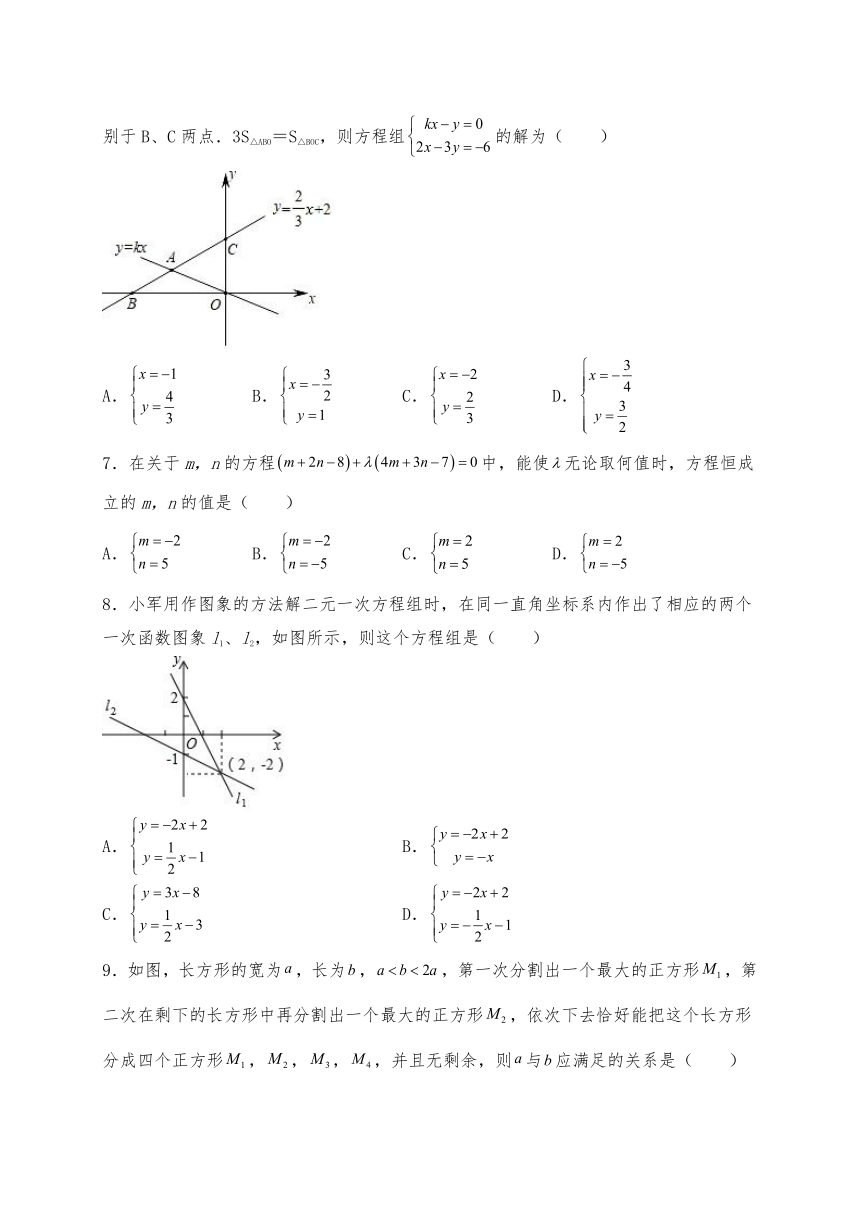
6.如图,直线y=kx(k≠0)与y=x+2在第二象限交于A,y=x+2交x轴,y轴分别于B、C两点.3S△ABO=S△BOC,则方程组的解为( )
A. B. C. D.
7.在关于m,n的方程中,能使无论取何值时,方程恒成立的m,n的值是( )
A. B. C. D.
8.小军用作图象的方法解二元一次方程组时,在同一直角坐标系内作出了相应的两个一次函数图象l1、l2,如图所示,则这个方程组是( )
A. B.
C. D.
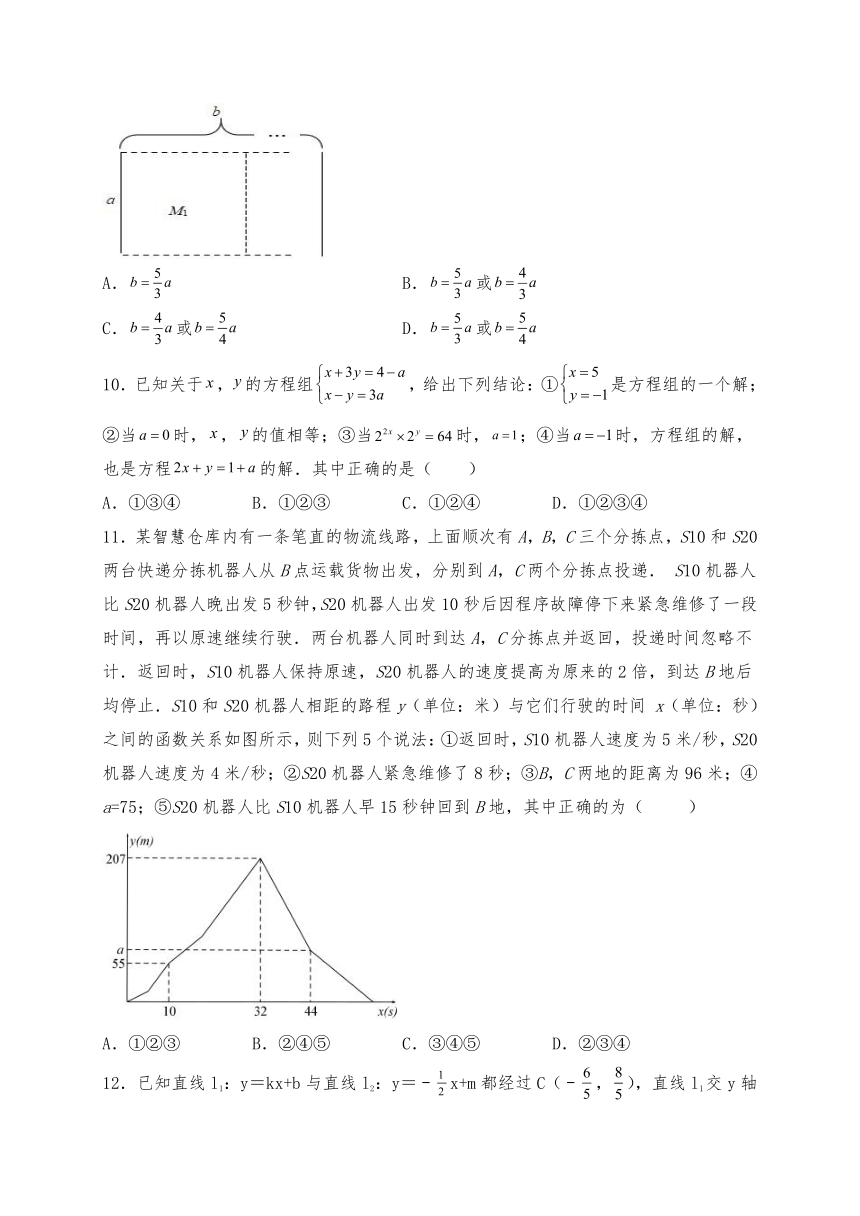
9.如图,长方形的宽为,长为,,第一次分割出一个最大的正方形,第二次在剩下的长方形中再分割出一个最大的正方形,依次下去恰好能把这个长方形分成四个正方形,,,,并且无剩余,则与应满足的关系是( )
A. B.或
C.或 D.或
10.已知关于,的方程组,给出下列结论:①是方程组的一个解;②当时,,的值相等;③当时,;④当时,方程组的解,也是方程的解.其中正确的是( )
A.①③④ B.①②③ C.①②④ D.①②③④
11.某智慧仓库内有一条笔直的物流线路,上面顺次有A,B,C三个分拣点,S10和S20两台快递分拣机器人从B点运载货物出发,分别到A,C两个分拣点投递. S10机器人比S20机器人晚出发5秒钟,S20机器人出发10秒后因程序故障停下来紧急维修了一段时间,再以原速继续行驶.两台机器人同时到达A,C分拣点并返回,投递时间忽略不计.返回时,S10机器人保持原速,S20机器人的速度提高为原来的2倍,到达B地后均停止.S10和S20机器人相距的路程y(单位:米)与它们行驶的时间 x(单位:秒)之间的函数关系如图所示,则下列5个说法:①返回时,S10机器人速度为5米/秒,S20机器人速度为4米/秒;②S20机器人紧急维修了8秒;③B,C两地的距离为96米;④a=75;⑤S20机器人比S10机器人早15秒钟回到B地,其中正确的为( )
A.①②③ B.②④⑤ C.③④⑤ D.②③④
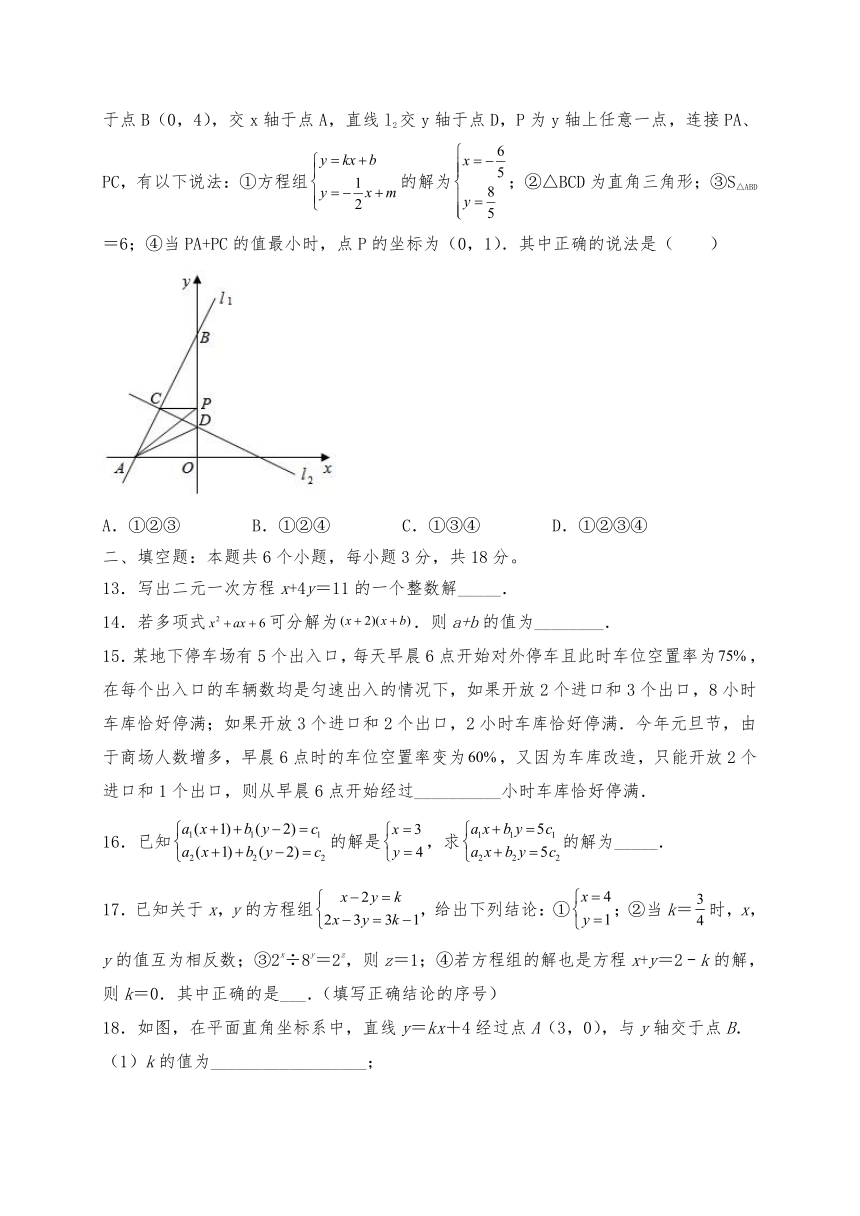
12.已知直线l1:y=kx+b与直线l2:y=﹣x+m都经过C(﹣,),直线l1交y轴于点B(0,4),交x轴于点A,直线l2交y轴于点D,P为y轴上任意一点,连接PA、PC,有以下说法:①方程组的解为;②△BCD为直角三角形;③S△ABD=6;④当PA+PC的值最小时,点P的坐标为(0,1).其中正确的说法是( )
A.①②③ B.①②④ C.①③④ D.①②③④
二、填空题:本题共6个小题,每小题3分,共18分。
13.写出二元一次方程x+4y=11的一个整数解_____.
14.若多项式可分解为.则a+b的值为________.
15.某地下停车场有5个出入口,每天早晨6点开始对外停车且此时车位空置率为,在每个出入口的车辆数均是匀速出入的情况下,如果开放2个进口和3个出口,8小时车库恰好停满;如果开放3个进口和2个出口,2小时车库恰好停满.今年元旦节,由于商场人数增多,早晨6点时的车位空置率变为,又因为车库改造,只能开放2个进口和1个出口,则从早晨6点开始经过__________小时车库恰好停满.
16.已知的解是,求的解为_____.
17.已知关于x,y的方程组,给出下列结论:①;②当k=时,x,y的值互为相反数;③2x÷8y=2z,则z=1;④若方程组的解也是方程x+y=2﹣k的解,则k=0.其中正确的是___.(填写正确结论的序号)
18.如图,在平面直角坐标系中,直线y=kx+4经过点A(3,0),与y轴交于点B.
(1)k的值为__________________;
(2)y轴上有点M(0,),线段AB上存在两点P,Q,使得以O,P,Q为顶点的三角形与OMP全等,则符合条件的点P的坐标为__________________.
三、解答题(19题6分,其余每题8分,共46分)
19.甲、乙两位同学在解方程组时,甲把字母看错了得到了方程组的解为;乙把字母看错了得到方程组的解为.
(1)求的值;
(2)求原方程组的解.
20.(2021·全国·八年级专题练习)解下列方程组:
(1) (2)
21.疫情期间,为满足市场需求,某厂家每天定量生产医用口罩和N95口罩共80万个.当该厂家生产的两种口罩当日全部售出时,则可获得利润35万元.两种口罩的成本和售价如下表所示:
成本(元/个) 售价(元/个)
医用口罩 0.8 1.2
N95口罩 2.5 3
(1)求每天定量生产这两种口罩各多少万个?(列方程组求解)
(2)该厂家将每天生产的口罩打包(每包1万个)并进行整包批发销售.为了支持防疫工作,现从生产的两种口罩中分别抽取若干包口罩免费捐赠给疫情严重的地区,且捐赠的N95口罩包数不超过医用口罩的包数.若该企业把捐赠后剩余的口罩全部售出后,每日仍可盈利2万元,求从医用口罩和N95口罩中各抽取多少包?
22.对a,b定义一种新运算T,规定:T(a,b)=(a+2b)(ax+by)(其中x,y均为非零实数).例如:T(1,1)=3x+3y.
(1)已知T(1,﹣1)=0,T(0,2)=8,求x,y的值;
(2)已知关于x,y的方程组,若a≥﹣2,求x+y的取值范围;
(3)在(2)的条件下,已知平面直角坐标系上的点A(x,y)落在坐标轴上,将线段OA沿x轴向右平移2个单位,得线段O′A′,坐标轴上有一点B满足三角形BOA′的面积为9,请直接写出点B的坐标.
23.某企业用规格是170cm×40cm的标准板材作为原材料,按照图①所示的裁法一或裁法二,裁剪出甲型与乙型两种板材(单位:cm).
(1)求图中a、b的值;
(2)若将40张标准板材按裁法一裁剪,5张标准板材按裁法二裁剪,裁剪后将得到的甲型与乙型板材做侧面或底面,做成如图②所示的竖式与横式两种无盖的装饰盒若干个(接缝处的长度忽略不计).
①一共可裁剪出甲型板材 张,乙型板材 张;
②恰好一共可以做出竖式和横式两种无盖装饰盒子多少个?
24.如图,在平面直角坐标系中,直线l1:y=x+4交y轴于点A,直线l2:y=﹣x与l1交于点B.
(1)求点B的坐标;
(2)在y轴左侧,有一条平行于y轴的动直线,分别与l1,l2交于点M、N,且点M在点N的上方.
①当MN=2时,求△BMN的面积;
②点Q为y轴上一动点若△MNQ是以NQ为直角边的直角三角形,且两直角边长之比为3∶4,求出满足条件所有点Q的坐标.
答案
一、选择题
D.D.C.D .D.C.A.D.B.D.B.B.
二、填空题。
13.(答案不唯一).
14.8.
15..
16..
17.①②③④.
18.(1)﹣ (2) (,)或(,)
三、解答题
19.
解:(1),
根据题意可知:
将,代入方程②,得
,
解得,
将,代入方程①,得
,
解得,
;
(2)由(1)知方程组为:
,
①②,得
,
把代入①得,,
原方程组的解为.
20.
解:(1)将“”看作整体:,
由①得, ③
将③代入②得 ,即, ④
将④代入③,化简得,即,
将代入④得,
所以原方程组的解为 .
(2)
由①得, ③
将③代入②,整理得,解得,
将代入③得,
所以原方程组的解为.
21.解:(1)设每天生产医用口罩x万个,生产N95口罩y万个,
依题意,得
解得
答:每天生产医用口罩50万个,生产N95口罩30万个.
(2)设从医用口罩中抽取m包,N95口罩中抽取n包,
依题意,得,
∴.
∵m,n均为正整数,
∴,,,,.
又∵捐赠的N95口罩不超过医用口罩的包数,
∴,,,.
答:从医用口罩中抽取10包、从N95口罩中抽取7包或从医用口罩中15包、从N95口罩中抽取5包或从医用口罩中抽取20包、从N95口罩中抽取3包或从医用口罩中抽取25包、从N95口罩中抽取1包.
22.
解:(1)根据新运算的定义可得:
,
解得:;
(2)由题意得:,
解得:,
,
,
,
,
;
(3)由(2)知,,
,
将线段沿轴向右平移2个单位,得线段,
,
点落在坐标轴上,且,
或,
或;
①当时,,
若点在轴上,,
,
或;
若点在轴上,,
,
或;
②当时,;
点只能在轴上,,
,
或;
综上所述,点的坐标为或或或或或.
23.
解:(1)依题意,得:
解得:a=60 b=40
答:a、b的值分别为60,40 .
(2)①一共可裁剪出甲型板材40×2+5=85(张)
乙型板材40+5×2=50(张).
故答案是:85,50;
②设可做成m个竖式无盖装饰盒,n个横式无盖装饰盒.
依题意得:,
解得:m=4,n=23
所以m+n=27,故答案为27个
24.
解:(1)∵直线l2:y=﹣x与l1交于点B,
∴联立方程组可得,
解得:,
∴B点坐标为(﹣2,2);
(2)①如图,设平行于y轴的动直线为:直线x=m,
过点B作BC⊥y轴,交直线x=m于点D,
∴M点坐标为(m,m+4),N点坐标为(m,﹣m),
∴MN=m+4﹣(﹣m)=2,
解得:m=﹣1,
又∵B点坐标为(﹣2,2),
∴BD=﹣1﹣(﹣2)=1,
∴S△BMN=MN BD==1;
②如图,
i)在Rt△MNQ中,当MN∶QN=3∶4时,
设MN=3a,QN=4a,
∴N点坐标为(﹣4a,4a),M点坐标为(﹣4a,﹣4a+4),Q点坐标为(0,4a),
∴MN=﹣4a+4﹣4a=3a,
解得:a=,
∴Q点坐标为(0,),
ii)在Rt△MNQ中,当QN∶MN=3∶4时,
设MN=4a,QN=3a,
∴N点坐标为(﹣3a,3a),M点坐标为(﹣3a,﹣3a+4),Q点坐标为(0,3a),
∴MN=﹣3a+4﹣3a=4a,
解得:a=,
∴Q点坐标为(0,),
综上,Q点坐标为(0,)或(0,).
一、选择题:本题共12个小题,每小题3分,共36分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.我国古代数学名著《孙子算经》中记载了一道题,大意是:有100匹马恰好拉了100片瓦,已知1匹大马能拉3片瓦,3匹小马能拉1片瓦,问有多少匹大马、多少匹小马?若设大马有x匹,小马有y匹,那么可列方程组为( )
A. B.
C. D.
2.某商场新购进一种服装,每套售价1000元,若将裤子降价10%,上衣涨价5%,调价后这套服装的单价比原来提高了2%,则调价前上衣的单价是( )
A.200元 B.480元 C.600元 D.800元
3.大课间,12人跳绳队为尊重每个队员的意愿,准备把队员分成跳大绳组或跳小绳组,大绳组3人一组,小绳组2人一组,在全队同学能同时参加活动且符合小组规定人数的前提下,则不同的分组方法有( )
A.1种 B.2种 C.3种 D.4种
4.已知关于,的方程组与有相同的解,则,的值为( )
A. B. C. D.
5.已知关于,的方程组,给出下列说法:①当时,方程组的解也是方程的一个解;②当时,;③不论取什么实数,的值始终不变;④若,则以上四种说法中正确的有( )个
A.1 B.2 C.3 D.4
6.如图,直线y=kx(k≠0)与y=x+2在第二象限交于A,y=x+2交x轴,y轴分别于B、C两点.3S△ABO=S△BOC,则方程组的解为( )
A. B. C. D.
7.在关于m,n的方程中,能使无论取何值时,方程恒成立的m,n的值是( )
A. B. C. D.
8.小军用作图象的方法解二元一次方程组时,在同一直角坐标系内作出了相应的两个一次函数图象l1、l2,如图所示,则这个方程组是( )
A. B.
C. D.
9.如图,长方形的宽为,长为,,第一次分割出一个最大的正方形,第二次在剩下的长方形中再分割出一个最大的正方形,依次下去恰好能把这个长方形分成四个正方形,,,,并且无剩余,则与应满足的关系是( )
A. B.或
C.或 D.或
10.已知关于,的方程组,给出下列结论:①是方程组的一个解;②当时,,的值相等;③当时,;④当时,方程组的解,也是方程的解.其中正确的是( )
A.①③④ B.①②③ C.①②④ D.①②③④
11.某智慧仓库内有一条笔直的物流线路,上面顺次有A,B,C三个分拣点,S10和S20两台快递分拣机器人从B点运载货物出发,分别到A,C两个分拣点投递. S10机器人比S20机器人晚出发5秒钟,S20机器人出发10秒后因程序故障停下来紧急维修了一段时间,再以原速继续行驶.两台机器人同时到达A,C分拣点并返回,投递时间忽略不计.返回时,S10机器人保持原速,S20机器人的速度提高为原来的2倍,到达B地后均停止.S10和S20机器人相距的路程y(单位:米)与它们行驶的时间 x(单位:秒)之间的函数关系如图所示,则下列5个说法:①返回时,S10机器人速度为5米/秒,S20机器人速度为4米/秒;②S20机器人紧急维修了8秒;③B,C两地的距离为96米;④a=75;⑤S20机器人比S10机器人早15秒钟回到B地,其中正确的为( )
A.①②③ B.②④⑤ C.③④⑤ D.②③④
12.已知直线l1:y=kx+b与直线l2:y=﹣x+m都经过C(﹣,),直线l1交y轴于点B(0,4),交x轴于点A,直线l2交y轴于点D,P为y轴上任意一点,连接PA、PC,有以下说法:①方程组的解为;②△BCD为直角三角形;③S△ABD=6;④当PA+PC的值最小时,点P的坐标为(0,1).其中正确的说法是( )
A.①②③ B.①②④ C.①③④ D.①②③④
二、填空题:本题共6个小题,每小题3分,共18分。
13.写出二元一次方程x+4y=11的一个整数解_____.
14.若多项式可分解为.则a+b的值为________.
15.某地下停车场有5个出入口,每天早晨6点开始对外停车且此时车位空置率为,在每个出入口的车辆数均是匀速出入的情况下,如果开放2个进口和3个出口,8小时车库恰好停满;如果开放3个进口和2个出口,2小时车库恰好停满.今年元旦节,由于商场人数增多,早晨6点时的车位空置率变为,又因为车库改造,只能开放2个进口和1个出口,则从早晨6点开始经过__________小时车库恰好停满.
16.已知的解是,求的解为_____.
17.已知关于x,y的方程组,给出下列结论:①;②当k=时,x,y的值互为相反数;③2x÷8y=2z,则z=1;④若方程组的解也是方程x+y=2﹣k的解,则k=0.其中正确的是___.(填写正确结论的序号)
18.如图,在平面直角坐标系中,直线y=kx+4经过点A(3,0),与y轴交于点B.
(1)k的值为__________________;
(2)y轴上有点M(0,),线段AB上存在两点P,Q,使得以O,P,Q为顶点的三角形与OMP全等,则符合条件的点P的坐标为__________________.
三、解答题(19题6分,其余每题8分,共46分)
19.甲、乙两位同学在解方程组时,甲把字母看错了得到了方程组的解为;乙把字母看错了得到方程组的解为.
(1)求的值;
(2)求原方程组的解.
20.(2021·全国·八年级专题练习)解下列方程组:
(1) (2)
21.疫情期间,为满足市场需求,某厂家每天定量生产医用口罩和N95口罩共80万个.当该厂家生产的两种口罩当日全部售出时,则可获得利润35万元.两种口罩的成本和售价如下表所示:
成本(元/个) 售价(元/个)
医用口罩 0.8 1.2
N95口罩 2.5 3
(1)求每天定量生产这两种口罩各多少万个?(列方程组求解)
(2)该厂家将每天生产的口罩打包(每包1万个)并进行整包批发销售.为了支持防疫工作,现从生产的两种口罩中分别抽取若干包口罩免费捐赠给疫情严重的地区,且捐赠的N95口罩包数不超过医用口罩的包数.若该企业把捐赠后剩余的口罩全部售出后,每日仍可盈利2万元,求从医用口罩和N95口罩中各抽取多少包?
22.对a,b定义一种新运算T,规定:T(a,b)=(a+2b)(ax+by)(其中x,y均为非零实数).例如:T(1,1)=3x+3y.
(1)已知T(1,﹣1)=0,T(0,2)=8,求x,y的值;
(2)已知关于x,y的方程组,若a≥﹣2,求x+y的取值范围;
(3)在(2)的条件下,已知平面直角坐标系上的点A(x,y)落在坐标轴上,将线段OA沿x轴向右平移2个单位,得线段O′A′,坐标轴上有一点B满足三角形BOA′的面积为9,请直接写出点B的坐标.
23.某企业用规格是170cm×40cm的标准板材作为原材料,按照图①所示的裁法一或裁法二,裁剪出甲型与乙型两种板材(单位:cm).
(1)求图中a、b的值;
(2)若将40张标准板材按裁法一裁剪,5张标准板材按裁法二裁剪,裁剪后将得到的甲型与乙型板材做侧面或底面,做成如图②所示的竖式与横式两种无盖的装饰盒若干个(接缝处的长度忽略不计).
①一共可裁剪出甲型板材 张,乙型板材 张;
②恰好一共可以做出竖式和横式两种无盖装饰盒子多少个?
24.如图,在平面直角坐标系中,直线l1:y=x+4交y轴于点A,直线l2:y=﹣x与l1交于点B.
(1)求点B的坐标;
(2)在y轴左侧,有一条平行于y轴的动直线,分别与l1,l2交于点M、N,且点M在点N的上方.
①当MN=2时,求△BMN的面积;
②点Q为y轴上一动点若△MNQ是以NQ为直角边的直角三角形,且两直角边长之比为3∶4,求出满足条件所有点Q的坐标.
答案
一、选择题
D.D.C.D .D.C.A.D.B.D.B.B.
二、填空题。
13.(答案不唯一).
14.8.
15..
16..
17.①②③④.
18.(1)﹣ (2) (,)或(,)
三、解答题
19.
解:(1),
根据题意可知:
将,代入方程②,得
,
解得,
将,代入方程①,得
,
解得,
;
(2)由(1)知方程组为:
,
①②,得
,
把代入①得,,
原方程组的解为.
20.
解:(1)将“”看作整体:,
由①得, ③
将③代入②得 ,即, ④
将④代入③,化简得,即,
将代入④得,
所以原方程组的解为 .
(2)
由①得, ③
将③代入②,整理得,解得,
将代入③得,
所以原方程组的解为.
21.解:(1)设每天生产医用口罩x万个,生产N95口罩y万个,
依题意,得
解得
答:每天生产医用口罩50万个,生产N95口罩30万个.
(2)设从医用口罩中抽取m包,N95口罩中抽取n包,
依题意,得,
∴.
∵m,n均为正整数,
∴,,,,.
又∵捐赠的N95口罩不超过医用口罩的包数,
∴,,,.
答:从医用口罩中抽取10包、从N95口罩中抽取7包或从医用口罩中15包、从N95口罩中抽取5包或从医用口罩中抽取20包、从N95口罩中抽取3包或从医用口罩中抽取25包、从N95口罩中抽取1包.
22.
解:(1)根据新运算的定义可得:
,
解得:;
(2)由题意得:,
解得:,
,
,
,
,
;
(3)由(2)知,,
,
将线段沿轴向右平移2个单位,得线段,
,
点落在坐标轴上,且,
或,
或;
①当时,,
若点在轴上,,
,
或;
若点在轴上,,
,
或;
②当时,;
点只能在轴上,,
,
或;
综上所述,点的坐标为或或或或或.
23.
解:(1)依题意,得:
解得:a=60 b=40
答:a、b的值分别为60,40 .
(2)①一共可裁剪出甲型板材40×2+5=85(张)
乙型板材40+5×2=50(张).
故答案是:85,50;
②设可做成m个竖式无盖装饰盒,n个横式无盖装饰盒.
依题意得:,
解得:m=4,n=23
所以m+n=27,故答案为27个
24.
解:(1)∵直线l2:y=﹣x与l1交于点B,
∴联立方程组可得,
解得:,
∴B点坐标为(﹣2,2);
(2)①如图,设平行于y轴的动直线为:直线x=m,
过点B作BC⊥y轴,交直线x=m于点D,
∴M点坐标为(m,m+4),N点坐标为(m,﹣m),
∴MN=m+4﹣(﹣m)=2,
解得:m=﹣1,
又∵B点坐标为(﹣2,2),
∴BD=﹣1﹣(﹣2)=1,
∴S△BMN=MN BD==1;
②如图,
i)在Rt△MNQ中,当MN∶QN=3∶4时,
设MN=3a,QN=4a,
∴N点坐标为(﹣4a,4a),M点坐标为(﹣4a,﹣4a+4),Q点坐标为(0,4a),
∴MN=﹣4a+4﹣4a=3a,
解得:a=,
∴Q点坐标为(0,),
ii)在Rt△MNQ中,当QN∶MN=3∶4时,
设MN=4a,QN=3a,
∴N点坐标为(﹣3a,3a),M点坐标为(﹣3a,﹣3a+4),Q点坐标为(0,3a),
∴MN=﹣3a+4﹣3a=4a,
解得:a=,
∴Q点坐标为(0,),
综上,Q点坐标为(0,)或(0,).
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
