空间向量与立体几何试卷(含答案)
文档属性
| 名称 | 空间向量与立体几何试卷(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 516.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-18 15:09:13 | ||
图片预览




文档简介
空间向量与立体几何测试(时间:120分钟 满分:150分)
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知向量,,满足||=||+||,则有( )
A.=+ B.=--
C.与同向 D.与同向
2.设向量a,b满足|a+b|=,|a-b|=,则a·b等于( )
A.1 B.2 C.3 D.5
3.在长方体ABCD A1B1C1D1中,AC与BD的交点为M,设=a,=b,=c,则下列向量中与相等的向量是 ( )
A.-a+b+c B.a+b+c
C.a-b+c D.-a-b+c
4.已知三棱锥P ABC中,PA⊥平面ABC,AB⊥AC,且PA=AB=AC=1.如图建立空间直角坐标系Axyz.设G为△PBC的重心,则的坐标为( )
A. B.
C. D.
5.设{i,j,k}是单位正交基底,已知向量p在基底{a,b,c}下的坐标为(8,6,4),其中a=i+j,b=j+k,c=k+i,则向量p在基底{i,j,k}下的坐标是( )
A.(12,14,10) B.(10,12,14)
C.(14,12,10) D.(4,3,2)
6.若a=(a1,a2,a3),b=(b1,b2,b3),则==是a∥b的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
7.如图所示,在正方体ABCD A1B1C1D1中,E,F分别在A1D,AC上,且A1E=A1D,AF=AC,则( )
A.EF至多与A1D,AC之一垂直
B.EF⊥A1D,EF⊥AC
C.EF与BD1相交
D.EF与BD1异面
8.已知点A,B,C的坐标分别为(0,1,0),(-1,0,1),(2,1,1),点P的坐标为(x,0,z),若PA⊥AB,PA⊥AC,则x-z=( )
A. B.- C.- D.1
二、选择题:本题共4小题,每小题5分,共20分。在每小题给出的选项中,有多项符合题目要求。全部选对的得5分,有选错的得0分,部分选对的得2分。
9.若n=(2,-3,1)是平面α的一个法向量,则下列向量中能作为平面α法向量的是( )
A.n1=(-2,3,-1) B.n2=(200,-300,100)
C.n3=(2,-3,) D.n4=(-2,3,0)
10.设a,b,c是任意的非零空间向量,且它们互不共线,给出下列命题,其中正确的是( )
A.(a·b)c-(c·a)b=0
B.|a|-|b|<|a-b|
C.(b·a)c-(c·a)b一定不与c垂直
D.(3a+2b)·(3a-2b)=9|a|2-4|b|2
11.已知向量a=(1,2,3),b=(3,0,-1),c=(-1,5,-3),下列等式中正确的是( )
A.(a·b)c=b·c
B.(a+b)·c=a·(b+c)
C.(a+b+c)2=a2+b2+c2
D.|a+b+c|=|a-b-c|
12.正三棱柱ABC A1B1C1中,AA1=AB,则( )
A.AC1与底面ABC所成角的正弦值为
B.AC1与底面ABC所成角的正弦值为
C.AC1与侧面AA1B1B所成角的正弦值为
D.AC1与侧面AA1B1B所成角的正弦值为
三、填空题:本题共4小题,每小题5分,共20分。把答案填在题中横线上。
13.已知平面α的一个法向量n=,A∈α,P α,且=,则直线PA与平面α所成的角为________.
14.在△ABC中,A(1,-2,-1),B(0,-3,1),C(2,-2,1). 若向量n是与共线的单位向量,则向量n的坐标为________;若向量n与平面ABC垂直,且|n|=,则n的坐标为________.
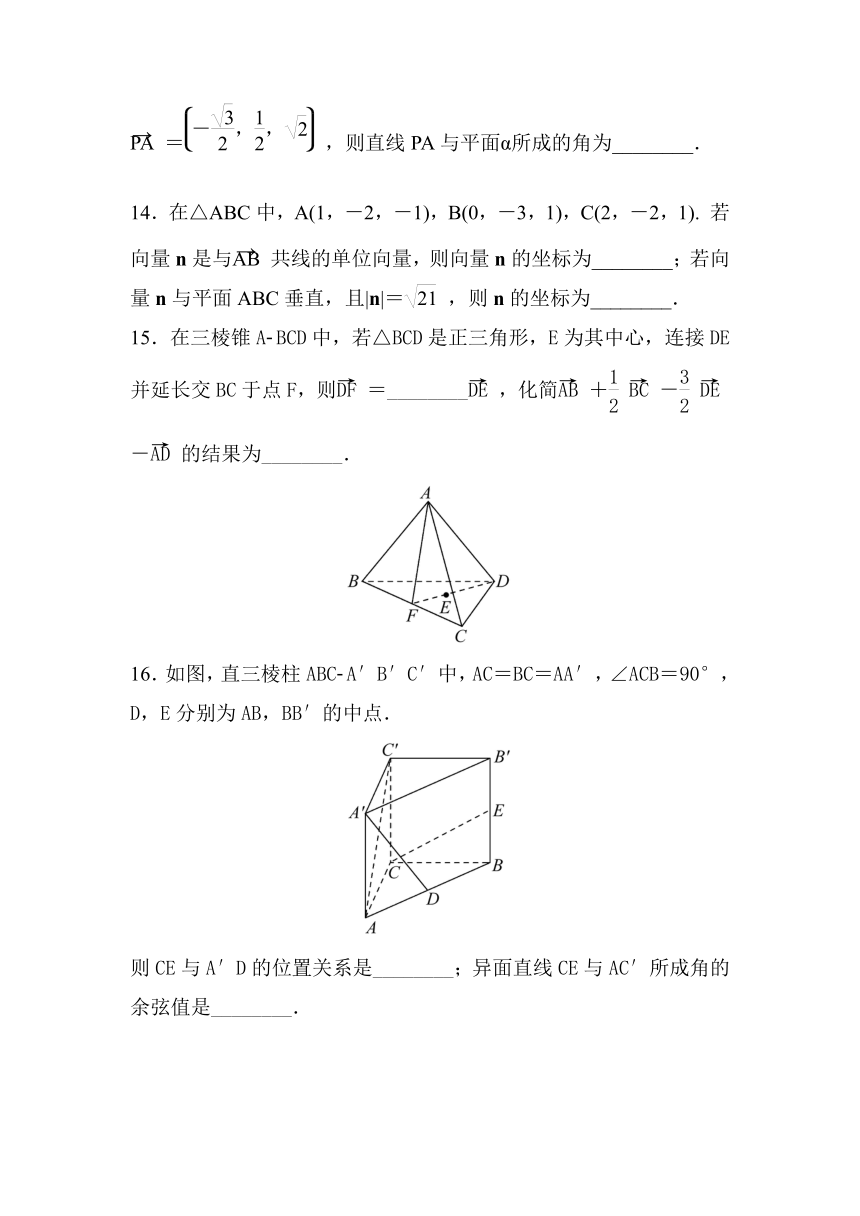
15.在三棱锥A BCD中,若△BCD是正三角形,E为其中心,连接DE并延长交BC于点F,则=________,化简+--的结果为________.
16.如图,直三棱柱ABC A′B′C′中,AC=BC=AA′,∠ACB=90°,D,E分别为AB,BB′的中点.
则CE与A′D的位置关系是________;异面直线CE与AC′所成角的余弦值是________.
四、解答题:本题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17.(本小题满分10分)
如图所示,在正方体ABCD A1B1C1D1中,求异面直线A1B与AC所成的角。
18.(本小题满分12分)
如图所示,在三棱锥A BCD中,E,F分别是AD,BC的中点,设=a,=b,=c,以{a,b,c}为空间的一个基底,求直线EF的一个方向向量。
19.(本小题满分12分)
如图,在四棱锥P ABCD中,PA⊥平面ABCD,AB=4,BC=3,AD=5,∠DAB=∠ABC=90°,E是CD的中点。求证:CD⊥平面PAE。
20.(本小题满分12分)
如图所示,四边形ABCD为矩形,PA⊥平面ABCD,PA=AD,M,N,Q分别是PC,AB,CD的中点。
求证:(1)MN∥平面PAD;
(2)平面QMN∥平面PAD。
21.(本小题满分12分)
如图,在长方体ABCD A1B1C1D1中,点E,F分别在棱DD1,BB1上,且2DE=ED1,BF=2FB1。
(1)证明:点C1在平面AEF内;
(2)若AB=2,AD=1,AA1=3,求二面角A EF A1的正弦值。
22.(本小题满分12分)
如图,正四面体V ABC的高VD的中点为O,VC的中点为M。
(1)求证:AO,BO,CO两两垂直;
(2)求〈,〉。
参考答案
1【解析】选D.向量,,满足||=||+||,所以C在线段AB之间,所以与同向.
2【解析】选A.|a+b|2=(a+b)2=a2+2a·b+b2=10,
|a-b|2=(a-b)2=a2-2a·b+b2=6,将上面两式左、右两边分别相减得4a·b=4,所以a·b=1.
3【解析】选A.=+=+=+(+)
=+=c+(-a+b)=-a+b+c.
4【解析】选D.由题意,可知B(1,0,0),C(0,1,0),P(0,0,1).取BC的中点M,则M.连接PM.
因为G为△PBC的重心,设G的坐标为(x,y,z),由=,得(x,y,z-1)=,从而得G.则=.
5【解析】选A.依题意,知p=8a+6b+4c=8(i+j)+6(j+k)+4(k+i)=12i+14j+10k,故向量p在基底{i,j,k}下的坐标是(12,14,10).
6【解析】选A.设===λ,则有a=λb(b≠0),所以a∥b,即正推成立;若b=0,恒有a∥b但,,均无意义,逆推不成立.
7【解析】选B.建立分别以DA,DC,DD1所在直线为x,y,z轴的空间直角坐标系,不妨设正方体的棱长为1,
则=(1,0,1),= (-1,1,0),E,F,=,所以·=0,·=0,所以EF⊥A1D,EF⊥AC.
8【解析】选D.由题设,=(-x,1,-z),=(-1,-1,1),=(2,0,1),因为PA⊥AB,PA⊥AC,所以·=0,·=0,所以解之得x-z=1.
9【解析】选ABC.因为n1=-n,n2=100n,n3=n,所以n1∥n,n2∥n,n3∥n,即n1、n2、n3都能作为α的法向量.
10【解析】选BD.根据向量数量积的定义及性质,可知a·b和c·a是实数,而c与b不共线,故(a·b)c与(c·a)b不一定相等,故A错误;因为[(b·a)c-(c·a)b]·c=(b·a)c2-(c·a)(b·c),所以当a⊥b,且a⊥c或b⊥c时,[(b·a)c-(c·a)b]·c=0,即(b·a)c-(c·a)b与c垂直,故C错误;易知BD正确.
11【解析】选BCD.A.左边为向量,右边为实数,显然不相等,不正确;B.左边=(4,2,2)·(-1,5,-3)=0,右边=(1,2,3)·(2,5,-4)=2+10-12=0,所以左边=右边,因此正确.C.a+b+c=(3,7,-1),左边=32+72+(-1)2=59,右边=12+22+32+32+0+(-1)2+(-1)2+52+(-3)2=59,所以左边=右边,因此正确.
D.由C可得:左边=,因为a-b-c=(-1,-3,7),所以|a-b-c|=,所以左边=右边,因此正确.综上可得BCD正确.
12【解析】选BC.如图,取A1C1的中点E,AC的中点F,并连接EF,则EB1,EC1,EF三条直线两两垂直,
则分别以这三条直线为x轴,y轴,z轴建立如图所示空间直角坐标系.
设AB=2,则AA1=2,所以A1(0,-1,0),C1(0,1,0),A(0,-1,2),C(0,1,2),B1(,0,0),所以=.
底面ABC的其中一个法向量为m=,
所以AC1与底面ABC所成角的正弦值为===,A错B对.
因为A1B1的中点K的坐标为,所以侧面AA1B1B的其中一个法向量为=,所以AC1与侧面AA1B1B所成角的正弦值为===,故C对D错.
13【解析】设直线PA与平面α所成的角为θ,则sin θ====,
所以直线PA与平面α所成的角为.
答案:
14【解析】据题意,得=(-1,-1,2),=(1,0,2).
设n=(x,y,z),若向量n是与共线的单位向量,则可得n=或n=.若n与平面ABC垂直,则即可得又因为|n|=,所以=,解得y=4或y=-4.当y=4时,x=-2,z=1;当y=-4时,x=2,z=-1.所以n =(-2,4,1)或n=(2,-4,-1)
答案:或
(-2,4,1)或 (2,-4,-1)
15【解析】DF为正三角形BCD的中线,E为中心,
所以=,+=,+=+=,
故+--=0.
答案: 0
16【解析】设=a,=b,=c,
根据题意,|a|=|b|=|c|且a·b=b·c=c·a=0,所以=b+c,=-c+b-a.所以·=-c2+b2=0.所以⊥,即CE与A′D垂直;因为=-a+c,所以||=|a|.又||=|a|,·=(-a+c)·=c2=|a|2,所以cos 〈,〉==,即异面直线CE与AC′所成角的余弦值为.
答案:垂直
17【解析】 不妨设正方体的棱长为1,=a,=b,=c,
则|a|=|b|=|c|=1,a·b=b·c=c·a=0,=a-c,=a+b。
所以·=(a-c)·(a+b)=|a|2+a·b-a·c-b·c=1。而||=||=,所以cos〈,〉==,又0°≤〈,〉≤180°,所以〈,〉=60°。因此异面直线A1B与AC所成的角为60°。
18【解析】 =++=(-)-+=--=a-b-c。故直线EF的一个方向向量为a-b-c。
19证明 如图,以A为原点,AB,AD,AP所在直线分别为x轴、y轴、z轴建立空间直角坐标系。
设PA=h,则A(0,0,0),B(4,0,0),C(4,3,0),D(0,5,0),E(2,4,0),P(0,0,h)。易知=(-4,2,0),=(2,4,0),=(0,0,h)。因为·=-8+8+0=0,·=0,所以CD⊥AE,CD⊥AP。因为AP∩AE=A,所以CD⊥平面PAE。
20证明 (1)如图,以A为原点,以AB,AD,AP所在直线为x,y,z轴建立空间直角坐标系,
设B(b,0,0),D(0,d,0),P(0,0,d),则C(b,d,0),因为M,N,Q分别是PC,AB,CD的中点,所以M,N,Q,
所以=。因为平面PAD的一个法向量为m=(1,0,0),
且·m=0,即⊥m。又MN 平面PAD,故MN∥平面PAD。
(2)=(0,-d,0),⊥m,又QN 平面PAD,所以QN∥平面PAD。
又因为MN∩QN=N,所以平面QMN∥平面PAD。
21解 设AB=a,AD=b,AA1=c,如图,以C1为原点,的方向为x轴正方向,建立空间直角坐标系C1xyz。
(1)证明:连接C1F,则C1(0,0,0),A(a,b,c),E,F,=,=,得=,因此EA∥C1F,即A,E,F,C1四点共面,所以点C1在平面AEF内。
(2)由已知得A(2,1,3),E(2,0,2),F(0,1,1),A1(2,1,0),=(0,-1,-1),=(-2,0,-2),=(0,-1,2),=(-2,0,1)。
设n1=(x,y,z)为平面AEF的法向量,则即
可取n1=(-1,-1,1)。设n2为平面A1EF的法向量,则同理可取n2=。因为cos〈n1,n2〉==-,所以二面角A EF A1的正弦值为。
22解 (1)证明:设=a,=b,=c,正四面体的棱长为1,
则=(a+b+c),=(b+c-5a),=(a+c-5b),=(a+b-5c),a·b=a·c=b·c,|a|2=|b|2=|c|2,所以·=(b+c-5a)·(a+c-5b)=(18a·b-9|a|2)=(18×1×1×cos 60°-9)=0,所以⊥,即AO⊥BO。同理,AO⊥CO,BO⊥CO。所以AO,BO,CO两两垂直。
(2)=+=-(a+b+c)+c=(-2a-2b+c),所以||==。又||==,·=(-2a-2b+c)·(b+c-5a)=,所以cos〈,〉==。
所以〈,〉=。
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知向量,,满足||=||+||,则有( )
A.=+ B.=--
C.与同向 D.与同向
2.设向量a,b满足|a+b|=,|a-b|=,则a·b等于( )
A.1 B.2 C.3 D.5
3.在长方体ABCD A1B1C1D1中,AC与BD的交点为M,设=a,=b,=c,则下列向量中与相等的向量是 ( )
A.-a+b+c B.a+b+c
C.a-b+c D.-a-b+c
4.已知三棱锥P ABC中,PA⊥平面ABC,AB⊥AC,且PA=AB=AC=1.如图建立空间直角坐标系Axyz.设G为△PBC的重心,则的坐标为( )
A. B.
C. D.
5.设{i,j,k}是单位正交基底,已知向量p在基底{a,b,c}下的坐标为(8,6,4),其中a=i+j,b=j+k,c=k+i,则向量p在基底{i,j,k}下的坐标是( )
A.(12,14,10) B.(10,12,14)
C.(14,12,10) D.(4,3,2)
6.若a=(a1,a2,a3),b=(b1,b2,b3),则==是a∥b的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
7.如图所示,在正方体ABCD A1B1C1D1中,E,F分别在A1D,AC上,且A1E=A1D,AF=AC,则( )
A.EF至多与A1D,AC之一垂直
B.EF⊥A1D,EF⊥AC
C.EF与BD1相交
D.EF与BD1异面
8.已知点A,B,C的坐标分别为(0,1,0),(-1,0,1),(2,1,1),点P的坐标为(x,0,z),若PA⊥AB,PA⊥AC,则x-z=( )
A. B.- C.- D.1
二、选择题:本题共4小题,每小题5分,共20分。在每小题给出的选项中,有多项符合题目要求。全部选对的得5分,有选错的得0分,部分选对的得2分。
9.若n=(2,-3,1)是平面α的一个法向量,则下列向量中能作为平面α法向量的是( )
A.n1=(-2,3,-1) B.n2=(200,-300,100)
C.n3=(2,-3,) D.n4=(-2,3,0)
10.设a,b,c是任意的非零空间向量,且它们互不共线,给出下列命题,其中正确的是( )
A.(a·b)c-(c·a)b=0
B.|a|-|b|<|a-b|
C.(b·a)c-(c·a)b一定不与c垂直
D.(3a+2b)·(3a-2b)=9|a|2-4|b|2
11.已知向量a=(1,2,3),b=(3,0,-1),c=(-1,5,-3),下列等式中正确的是( )
A.(a·b)c=b·c
B.(a+b)·c=a·(b+c)
C.(a+b+c)2=a2+b2+c2
D.|a+b+c|=|a-b-c|
12.正三棱柱ABC A1B1C1中,AA1=AB,则( )
A.AC1与底面ABC所成角的正弦值为
B.AC1与底面ABC所成角的正弦值为
C.AC1与侧面AA1B1B所成角的正弦值为
D.AC1与侧面AA1B1B所成角的正弦值为
三、填空题:本题共4小题,每小题5分,共20分。把答案填在题中横线上。
13.已知平面α的一个法向量n=,A∈α,P α,且=,则直线PA与平面α所成的角为________.
14.在△ABC中,A(1,-2,-1),B(0,-3,1),C(2,-2,1). 若向量n是与共线的单位向量,则向量n的坐标为________;若向量n与平面ABC垂直,且|n|=,则n的坐标为________.
15.在三棱锥A BCD中,若△BCD是正三角形,E为其中心,连接DE并延长交BC于点F,则=________,化简+--的结果为________.
16.如图,直三棱柱ABC A′B′C′中,AC=BC=AA′,∠ACB=90°,D,E分别为AB,BB′的中点.
则CE与A′D的位置关系是________;异面直线CE与AC′所成角的余弦值是________.
四、解答题:本题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17.(本小题满分10分)
如图所示,在正方体ABCD A1B1C1D1中,求异面直线A1B与AC所成的角。
18.(本小题满分12分)
如图所示,在三棱锥A BCD中,E,F分别是AD,BC的中点,设=a,=b,=c,以{a,b,c}为空间的一个基底,求直线EF的一个方向向量。
19.(本小题满分12分)
如图,在四棱锥P ABCD中,PA⊥平面ABCD,AB=4,BC=3,AD=5,∠DAB=∠ABC=90°,E是CD的中点。求证:CD⊥平面PAE。
20.(本小题满分12分)
如图所示,四边形ABCD为矩形,PA⊥平面ABCD,PA=AD,M,N,Q分别是PC,AB,CD的中点。
求证:(1)MN∥平面PAD;
(2)平面QMN∥平面PAD。
21.(本小题满分12分)
如图,在长方体ABCD A1B1C1D1中,点E,F分别在棱DD1,BB1上,且2DE=ED1,BF=2FB1。
(1)证明:点C1在平面AEF内;
(2)若AB=2,AD=1,AA1=3,求二面角A EF A1的正弦值。
22.(本小题满分12分)
如图,正四面体V ABC的高VD的中点为O,VC的中点为M。
(1)求证:AO,BO,CO两两垂直;
(2)求〈,〉。
参考答案
1【解析】选D.向量,,满足||=||+||,所以C在线段AB之间,所以与同向.
2【解析】选A.|a+b|2=(a+b)2=a2+2a·b+b2=10,
|a-b|2=(a-b)2=a2-2a·b+b2=6,将上面两式左、右两边分别相减得4a·b=4,所以a·b=1.
3【解析】选A.=+=+=+(+)
=+=c+(-a+b)=-a+b+c.
4【解析】选D.由题意,可知B(1,0,0),C(0,1,0),P(0,0,1).取BC的中点M,则M.连接PM.
因为G为△PBC的重心,设G的坐标为(x,y,z),由=,得(x,y,z-1)=,从而得G.则=.
5【解析】选A.依题意,知p=8a+6b+4c=8(i+j)+6(j+k)+4(k+i)=12i+14j+10k,故向量p在基底{i,j,k}下的坐标是(12,14,10).
6【解析】选A.设===λ,则有a=λb(b≠0),所以a∥b,即正推成立;若b=0,恒有a∥b但,,均无意义,逆推不成立.
7【解析】选B.建立分别以DA,DC,DD1所在直线为x,y,z轴的空间直角坐标系,不妨设正方体的棱长为1,
则=(1,0,1),= (-1,1,0),E,F,=,所以·=0,·=0,所以EF⊥A1D,EF⊥AC.
8【解析】选D.由题设,=(-x,1,-z),=(-1,-1,1),=(2,0,1),因为PA⊥AB,PA⊥AC,所以·=0,·=0,所以解之得x-z=1.
9【解析】选ABC.因为n1=-n,n2=100n,n3=n,所以n1∥n,n2∥n,n3∥n,即n1、n2、n3都能作为α的法向量.
10【解析】选BD.根据向量数量积的定义及性质,可知a·b和c·a是实数,而c与b不共线,故(a·b)c与(c·a)b不一定相等,故A错误;因为[(b·a)c-(c·a)b]·c=(b·a)c2-(c·a)(b·c),所以当a⊥b,且a⊥c或b⊥c时,[(b·a)c-(c·a)b]·c=0,即(b·a)c-(c·a)b与c垂直,故C错误;易知BD正确.
11【解析】选BCD.A.左边为向量,右边为实数,显然不相等,不正确;B.左边=(4,2,2)·(-1,5,-3)=0,右边=(1,2,3)·(2,5,-4)=2+10-12=0,所以左边=右边,因此正确.C.a+b+c=(3,7,-1),左边=32+72+(-1)2=59,右边=12+22+32+32+0+(-1)2+(-1)2+52+(-3)2=59,所以左边=右边,因此正确.
D.由C可得:左边=,因为a-b-c=(-1,-3,7),所以|a-b-c|=,所以左边=右边,因此正确.综上可得BCD正确.
12【解析】选BC.如图,取A1C1的中点E,AC的中点F,并连接EF,则EB1,EC1,EF三条直线两两垂直,
则分别以这三条直线为x轴,y轴,z轴建立如图所示空间直角坐标系.
设AB=2,则AA1=2,所以A1(0,-1,0),C1(0,1,0),A(0,-1,2),C(0,1,2),B1(,0,0),所以=.
底面ABC的其中一个法向量为m=,
所以AC1与底面ABC所成角的正弦值为===,A错B对.
因为A1B1的中点K的坐标为,所以侧面AA1B1B的其中一个法向量为=,所以AC1与侧面AA1B1B所成角的正弦值为===,故C对D错.
13【解析】设直线PA与平面α所成的角为θ,则sin θ====,
所以直线PA与平面α所成的角为.
答案:
14【解析】据题意,得=(-1,-1,2),=(1,0,2).
设n=(x,y,z),若向量n是与共线的单位向量,则可得n=或n=.若n与平面ABC垂直,则即可得又因为|n|=,所以=,解得y=4或y=-4.当y=4时,x=-2,z=1;当y=-4时,x=2,z=-1.所以n =(-2,4,1)或n=(2,-4,-1)
答案:或
(-2,4,1)或 (2,-4,-1)
15【解析】DF为正三角形BCD的中线,E为中心,
所以=,+=,+=+=,
故+--=0.
答案: 0
16【解析】设=a,=b,=c,
根据题意,|a|=|b|=|c|且a·b=b·c=c·a=0,所以=b+c,=-c+b-a.所以·=-c2+b2=0.所以⊥,即CE与A′D垂直;因为=-a+c,所以||=|a|.又||=|a|,·=(-a+c)·=c2=|a|2,所以cos 〈,〉==,即异面直线CE与AC′所成角的余弦值为.
答案:垂直
17【解析】 不妨设正方体的棱长为1,=a,=b,=c,
则|a|=|b|=|c|=1,a·b=b·c=c·a=0,=a-c,=a+b。
所以·=(a-c)·(a+b)=|a|2+a·b-a·c-b·c=1。而||=||=,所以cos〈,〉==,又0°≤〈,〉≤180°,所以〈,〉=60°。因此异面直线A1B与AC所成的角为60°。
18【解析】 =++=(-)-+=--=a-b-c。故直线EF的一个方向向量为a-b-c。
19证明 如图,以A为原点,AB,AD,AP所在直线分别为x轴、y轴、z轴建立空间直角坐标系。
设PA=h,则A(0,0,0),B(4,0,0),C(4,3,0),D(0,5,0),E(2,4,0),P(0,0,h)。易知=(-4,2,0),=(2,4,0),=(0,0,h)。因为·=-8+8+0=0,·=0,所以CD⊥AE,CD⊥AP。因为AP∩AE=A,所以CD⊥平面PAE。
20证明 (1)如图,以A为原点,以AB,AD,AP所在直线为x,y,z轴建立空间直角坐标系,
设B(b,0,0),D(0,d,0),P(0,0,d),则C(b,d,0),因为M,N,Q分别是PC,AB,CD的中点,所以M,N,Q,
所以=。因为平面PAD的一个法向量为m=(1,0,0),
且·m=0,即⊥m。又MN 平面PAD,故MN∥平面PAD。
(2)=(0,-d,0),⊥m,又QN 平面PAD,所以QN∥平面PAD。
又因为MN∩QN=N,所以平面QMN∥平面PAD。
21解 设AB=a,AD=b,AA1=c,如图,以C1为原点,的方向为x轴正方向,建立空间直角坐标系C1xyz。
(1)证明:连接C1F,则C1(0,0,0),A(a,b,c),E,F,=,=,得=,因此EA∥C1F,即A,E,F,C1四点共面,所以点C1在平面AEF内。
(2)由已知得A(2,1,3),E(2,0,2),F(0,1,1),A1(2,1,0),=(0,-1,-1),=(-2,0,-2),=(0,-1,2),=(-2,0,1)。
设n1=(x,y,z)为平面AEF的法向量,则即
可取n1=(-1,-1,1)。设n2为平面A1EF的法向量,则同理可取n2=。因为cos〈n1,n2〉==-,所以二面角A EF A1的正弦值为。
22解 (1)证明:设=a,=b,=c,正四面体的棱长为1,
则=(a+b+c),=(b+c-5a),=(a+c-5b),=(a+b-5c),a·b=a·c=b·c,|a|2=|b|2=|c|2,所以·=(b+c-5a)·(a+c-5b)=(18a·b-9|a|2)=(18×1×1×cos 60°-9)=0,所以⊥,即AO⊥BO。同理,AO⊥CO,BO⊥CO。所以AO,BO,CO两两垂直。
(2)=+=-(a+b+c)+c=(-2a-2b+c),所以||==。又||==,·=(-2a-2b+c)·(b+c-5a)=,所以cos〈,〉==。
所以〈,〉=。
