第2章 整式的加减复习与小结 课件(共17张PPT)
文档属性
| 名称 | 第2章 整式的加减复习与小结 课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-19 09:12:36 | ||
图片预览






文档简介
(共17张PPT)
第2章整式的加减复习与小结
人教版数学七年级上册
复习目标
1.能用含有字母的式子表示实际问题中的数量关系;
2.理解单项式、多项式、整式的定义;
3.能准确找出单项式的系数、次数、多项式的项和次数;
4.熟练进行整式的加减运算;
5.会求代数式的值.
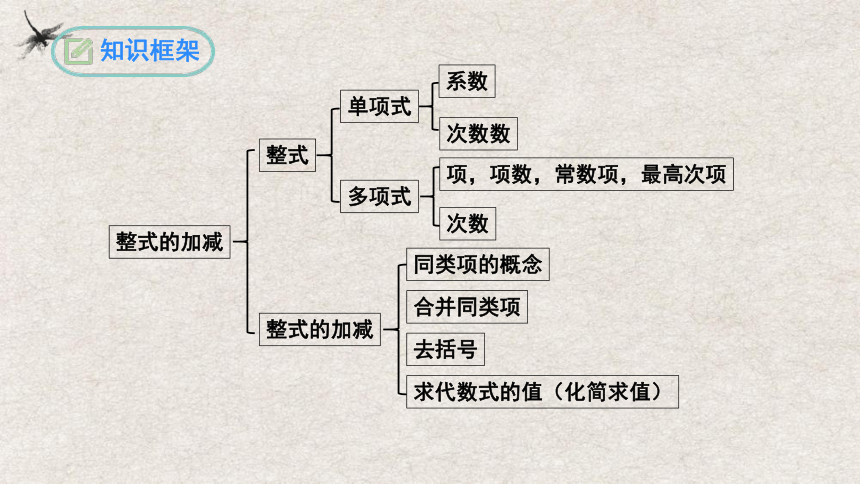
知识框架
整式的加减
整式
单项式
多项式
系数
次数
次数数
同类项的概念
整式的加减
合并同类项
去括号
项,项数,常数项,最高次项
求代数式的值(化简求值)
知识梳理
知识点一 整式的相关概念
1.都是数或字母的 ,这样的式子叫做单项式,单独的一个数或一个字母也是单项式.
2.单项式中的 叫做这个单项式的系数.
3.一个单项式中,所有字母的指数的 叫做这个单项式的次数.
积
数字因数
和
4.几个单项式的____叫做多项式.
5.多项式的次数:多项式里次数最高项的 ,叫做这个多项式的次数.
6.________________统称整式.
知识梳理
知识点一 整式的有关概念
和
单项式与多项式
次数
课堂检测
B
1.在式子3m+n,-2mn, p, ,0中,单项式的个数是( ) A.2 B.3 C.4 D.5
3
3.下列多项式次数为3的是( )
C
课堂检测
知识梳理
知识点二 同类项、合并同类项
1.所含字母______,并且相同字母的指数也______的项叫做同类项.几个常数项也是同类项.
2.把多项式中的 合并成一项,叫做合并同类项,即把它们的系数 作为新的系数,而字母及字母的指数 .
相同
相同
同类项
不变
相加
课堂检测
1.若5x3y与xmyn是同类项,则m= ,n= .
若单项式a3b与3am+nbn能合并,则m= ,n= .
3
1
2
1
2.若3xm+5y2与x4yn的和是单项式,求mn的值.
解:由题意得:m+5=4,n=2,
所以m=-1.
所以mn=(-1)2=1.
知识梳理
知识点三 去括号
去括号法则:
1.如果括号外的因数是 ,去括号后原括号内各项的符号与原来的符号 .
2.如果括号外的因数是 ,去括号后原括号内各项的符号与原来的符号 .
正数
相同
负数
相反
知识梳理
知识点三 去括号
【方法技巧】
去括号时应注意:
(1)括号前是“-”号,去括号时括号内各项要改变符号;
(2)运用乘法分配律时不要漏乘其中的项.
课堂检测
1.下列各项中,去括号正确的是( )
A.x2-(2x-y+2)=x2-2x+y+2
B.-(m+n)-mn=-m+n-mn
C.x-(5x-3y)+(2x-y)=-2x+2y
D.ab-(-ab+3)=3
C
课堂检测
2.已知A=x3+2y3-xy2,B=-y3+x3+2xy2,
求:(1)A+B;(2)2B-2A.
解:(1)A+B=(x3+2y3-xy2)+(-y3+x3+2xy2)
=x3+2y3-xy2-y3+x3+2xy2
=2x3+y3+xy2.
(2)2B-2A=2(-y3+x3+2xy2)-2(x3+2y3-xy2)
=-2y3+2x3+4xy2-2x3-4y3+2xy2
=6xy2-6y3.
1.有括号时先去括号;
2.找同类项,做好标记;
3.利用加法的交换律和结合律把同类项放在一起;
4.利用乘法分配律计算结果;
5.按要求按“升”或“降”幂排列.
找
搬
并
排
知识梳理
知识点四 整式的加减混合运算步骤
去
课堂检测
1.已知A=3x2-x+2,B=x+1,C= ,求3A+2B-36C的值,
其中x=-3.
当x=-3时,原式=-(-3)+24=3+24=27.
解:
2.化简后再求值:5x2-2y-8(x2-2y)+3(2x2-3y),其中|x+3|=0,y=2.
解:原式=5x2-2y-8x2+16y+6x2-9y=3x2-5y.
因为|x+3|=0,
所以x+3=0,
即x=-3,y=2,
所以,原式=27-10=17.
课堂检测
谢谢聆听
第2章整式的加减复习与小结
人教版数学七年级上册
复习目标
1.能用含有字母的式子表示实际问题中的数量关系;
2.理解单项式、多项式、整式的定义;
3.能准确找出单项式的系数、次数、多项式的项和次数;
4.熟练进行整式的加减运算;
5.会求代数式的值.
知识框架
整式的加减
整式
单项式
多项式
系数
次数
次数数
同类项的概念
整式的加减
合并同类项
去括号
项,项数,常数项,最高次项
求代数式的值(化简求值)
知识梳理
知识点一 整式的相关概念
1.都是数或字母的 ,这样的式子叫做单项式,单独的一个数或一个字母也是单项式.
2.单项式中的 叫做这个单项式的系数.
3.一个单项式中,所有字母的指数的 叫做这个单项式的次数.
积
数字因数
和
4.几个单项式的____叫做多项式.
5.多项式的次数:多项式里次数最高项的 ,叫做这个多项式的次数.
6.________________统称整式.
知识梳理
知识点一 整式的有关概念
和
单项式与多项式
次数
课堂检测
B
1.在式子3m+n,-2mn, p, ,0中,单项式的个数是( ) A.2 B.3 C.4 D.5
3
3.下列多项式次数为3的是( )
C
课堂检测
知识梳理
知识点二 同类项、合并同类项
1.所含字母______,并且相同字母的指数也______的项叫做同类项.几个常数项也是同类项.
2.把多项式中的 合并成一项,叫做合并同类项,即把它们的系数 作为新的系数,而字母及字母的指数 .
相同
相同
同类项
不变
相加
课堂检测
1.若5x3y与xmyn是同类项,则m= ,n= .
若单项式a3b与3am+nbn能合并,则m= ,n= .
3
1
2
1
2.若3xm+5y2与x4yn的和是单项式,求mn的值.
解:由题意得:m+5=4,n=2,
所以m=-1.
所以mn=(-1)2=1.
知识梳理
知识点三 去括号
去括号法则:
1.如果括号外的因数是 ,去括号后原括号内各项的符号与原来的符号 .
2.如果括号外的因数是 ,去括号后原括号内各项的符号与原来的符号 .
正数
相同
负数
相反
知识梳理
知识点三 去括号
【方法技巧】
去括号时应注意:
(1)括号前是“-”号,去括号时括号内各项要改变符号;
(2)运用乘法分配律时不要漏乘其中的项.
课堂检测
1.下列各项中,去括号正确的是( )
A.x2-(2x-y+2)=x2-2x+y+2
B.-(m+n)-mn=-m+n-mn
C.x-(5x-3y)+(2x-y)=-2x+2y
D.ab-(-ab+3)=3
C
课堂检测
2.已知A=x3+2y3-xy2,B=-y3+x3+2xy2,
求:(1)A+B;(2)2B-2A.
解:(1)A+B=(x3+2y3-xy2)+(-y3+x3+2xy2)
=x3+2y3-xy2-y3+x3+2xy2
=2x3+y3+xy2.
(2)2B-2A=2(-y3+x3+2xy2)-2(x3+2y3-xy2)
=-2y3+2x3+4xy2-2x3-4y3+2xy2
=6xy2-6y3.
1.有括号时先去括号;
2.找同类项,做好标记;
3.利用加法的交换律和结合律把同类项放在一起;
4.利用乘法分配律计算结果;
5.按要求按“升”或“降”幂排列.
找
搬
并
排
知识梳理
知识点四 整式的加减混合运算步骤
去
课堂检测
1.已知A=3x2-x+2,B=x+1,C= ,求3A+2B-36C的值,
其中x=-3.
当x=-3时,原式=-(-3)+24=3+24=27.
解:
2.化简后再求值:5x2-2y-8(x2-2y)+3(2x2-3y),其中|x+3|=0,y=2.
解:原式=5x2-2y-8x2+16y+6x2-9y=3x2-5y.
因为|x+3|=0,
所以x+3=0,
即x=-3,y=2,
所以,原式=27-10=17.
课堂检测
谢谢聆听
