三角形全等的条件[上学期]
文档属性
| 名称 | 三角形全等的条件[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 175.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-10-13 00:00:00 | ||
图片预览


文档简介
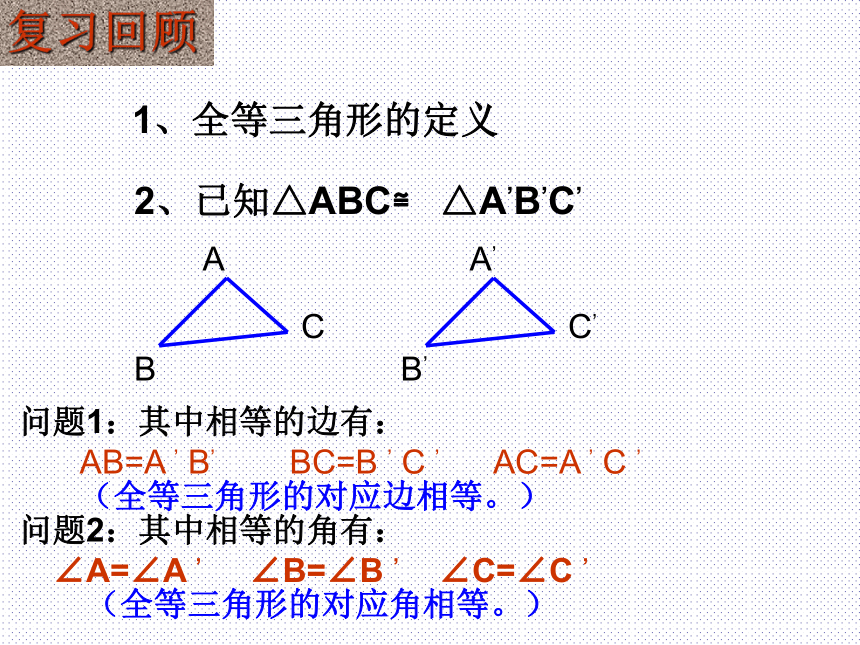
课件16张PPT。13.2 三角形全等的条件(1)复习回顾1、全等三角形的定义2、已知△ABC≌ △A’B’C’问题1:其中相等的边有:问题2:其中相等的角有:AB=A ’ B’BC=B ’ C ’AC=A ’ C ’∠A=∠A ’∠B=∠B ’∠C=∠C ’(全等三角形的对应边相等。)(全等三角形的对应角相等。)两个三角形全等三组对应边、三组对应角
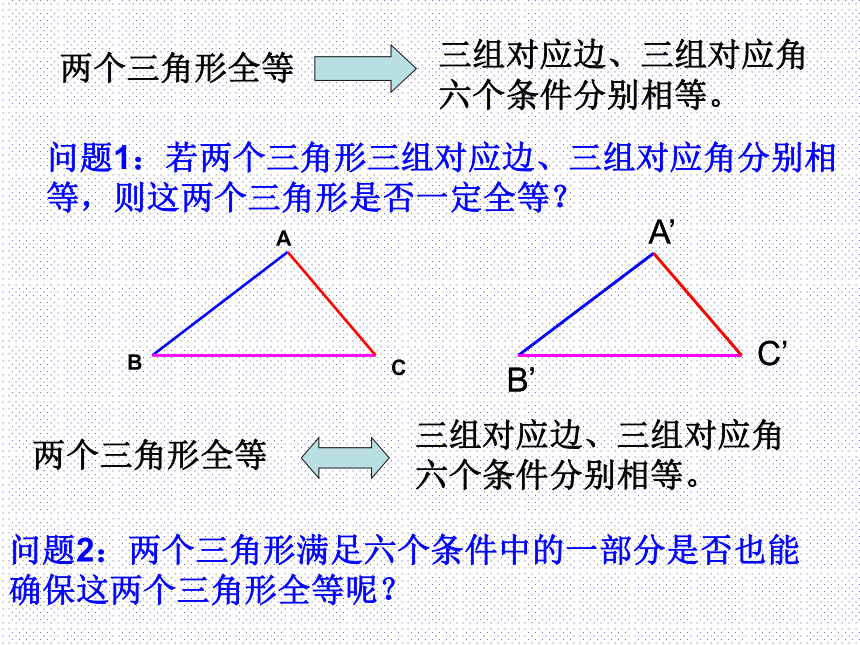
六个条件分别相等。问题1:若两个三角形三组对应边、三组对应角分别相等,则这两个三角形是否一定全等?两个三角形全等三组对应边、三组对应角
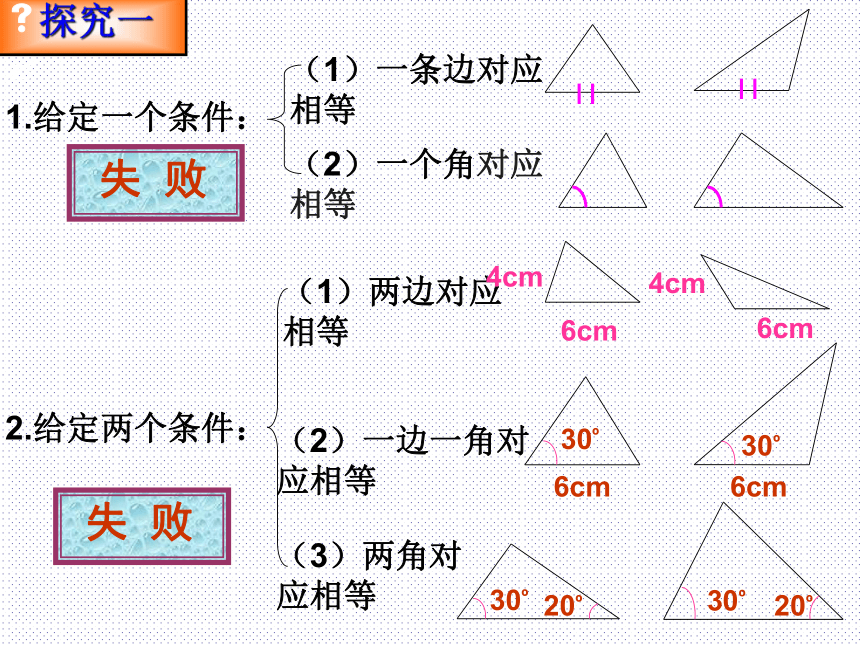
六个条件分别相等。问题2:两个三角形满足六个条件中的一部分是否也能确保这两个三角形全等呢??探究一 ? 1.给定一个条件:(1)一条边对应相等(2)一个角对应相等 失 败2.给定两个条件:(1)两边对应相等
(2)一边一角对应相等
(3)两角对应相等
失 败千万别泄气哦!俗话说:失败是成功之母!我们继续探究:?探究二 ? 给定三个条件:(1)三边对应相等
(2)两边一角对应相等
(3)一边两角对应相等
(4)三角对应相等
先任意画一个△ABC,再画一个△A’B’C’
使得A’B’=AB,B’C’=BC,A’C’=AC;
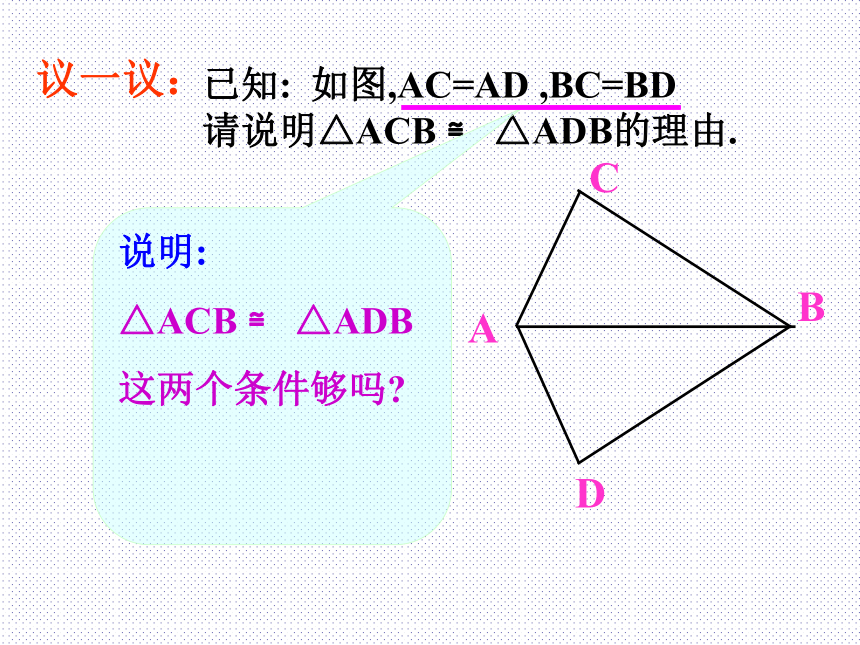
观察所得的两个三角形是否全等。[动手画一画] ? 三边对应相等的两个三角形全等。(可以简写成“边边边”或“SSS”)[想一想] 我们曾经做过这样的实验:将三根木条钉成一个三角形木架,这个三角形木架的形状、大小就不变了,即三角形具有稳定性,你能解释其中的道理吗?议一议:已知: 如图,AC=AD ,BC=BD 请说明△ACB ≌ △ADB的理由.
ABCD说明:
△ACB ≌ △ADB
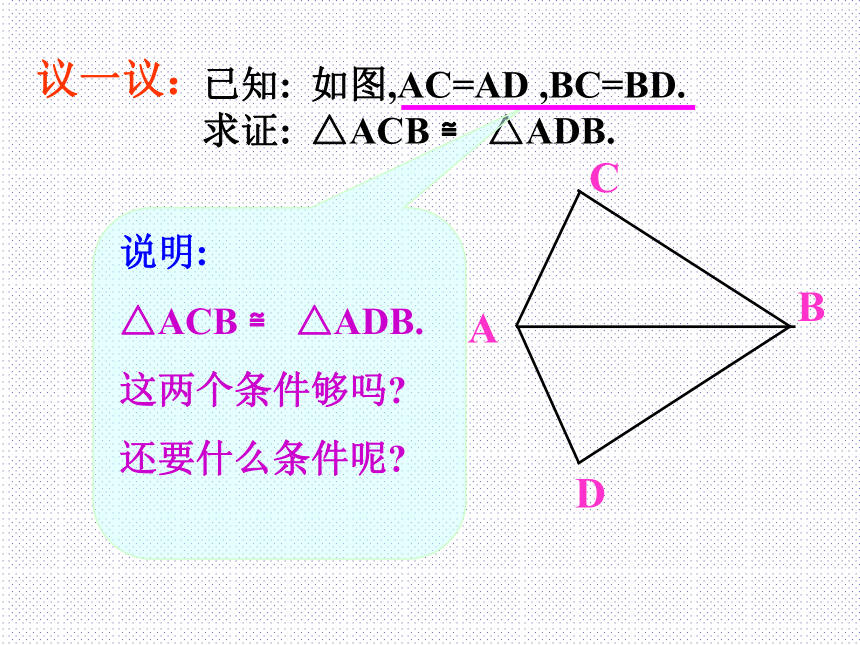
这两个条件够吗?已知: 如图,AC=AD ,BC=BD. 求证: △ACB ≌ △ADB.
ABCD说明:
△ACB ≌ △ADB.
这两个条件够吗?
还要什么条件呢?议一议:已知: 如图,AC=AD ,BC=BD. 求证: △ACB ≌ △ADB.
ABCD说明:
△ACB ≌ △ADB.
这两个条件够吗?
还要什么条件呢?还要一条边议一议:已知: 如图,AC=AD ,BC=BD. 求证: △ACB ≌ △ADB.
ABCD它既是△ACB的一条边,看看线段AB
又是△ADB的一条边
△ACB 和△ADB的公共边议一议:已知: 如图,AC=AD ,BC=BD. 求证: △ACB ≌ △ADB.
ABCD证明:在△ACB 和 △ADB中 AC = A D
BC = BD
A B = A B (公共边)∴△ACB≌△ADB(SSS)议一议:应用举例? 例1:如图所示,△ABC是一个钢架,AB=AC,AD是连接点A与BC中点D的支架。
求证:△ABD≌△ACD。证明:∵D是BC的中点∴BD=CD在△ABD和△ACD中AB=ACBD=CDAD=AD∴△ABD≌△ACD(SSS)像上述判断两个三角形全等的推理过程,
叫做证明三角形全等。(SSS)
如图,在四边形ABCD中
AB=CD,AD=CB,则∠A= ∠C
请说明理由。AB=CD (已知)AD=CB (已知)BD=DB(公共边)∴ ∠A= ∠C ( )
全等三角形的对应角相等知识连接练一练 ? 工人师傅常用角尺平分一个任意角,做法如下:如图,∠AOB是一个任意角,在边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与M、N重合,过角尺顶点C的射线OC便是∠AOB的平分线。为什么?已知如图所示,AC=FE,BC=DE,AD=FB,要用“边边边”证明△ABC≌△FDE,需要那些条件?如何证明??思考 ? 例2:如图,已知AB=CD,AD=CB,求证:∠B=∠D证明:连结AC,AB=CD(已知)AC=CA(公共边)CB=AD(已知)∴ △ ABC≌ △ CDA(SSS)∴ ∠B=∠D(全等三角形对应角相等)问:此题添加辅助线,若连结BD行吗?在原有条件下,还能推出什么结论?答:∠ABC=∠ADC,AB∥CD,AD∥BC在△ABC和△ ADC中小结:四边形问题转化为三角形问题解决。经过本节课的学习,你有哪些收获?小结
六个条件分别相等。问题1:若两个三角形三组对应边、三组对应角分别相等,则这两个三角形是否一定全等?两个三角形全等三组对应边、三组对应角
六个条件分别相等。问题2:两个三角形满足六个条件中的一部分是否也能确保这两个三角形全等呢??探究一 ? 1.给定一个条件:(1)一条边对应相等(2)一个角对应相等 失 败2.给定两个条件:(1)两边对应相等
(2)一边一角对应相等
(3)两角对应相等
失 败千万别泄气哦!俗话说:失败是成功之母!我们继续探究:?探究二 ? 给定三个条件:(1)三边对应相等
(2)两边一角对应相等
(3)一边两角对应相等
(4)三角对应相等
先任意画一个△ABC,再画一个△A’B’C’
使得A’B’=AB,B’C’=BC,A’C’=AC;
观察所得的两个三角形是否全等。[动手画一画] ? 三边对应相等的两个三角形全等。(可以简写成“边边边”或“SSS”)[想一想] 我们曾经做过这样的实验:将三根木条钉成一个三角形木架,这个三角形木架的形状、大小就不变了,即三角形具有稳定性,你能解释其中的道理吗?议一议:已知: 如图,AC=AD ,BC=BD 请说明△ACB ≌ △ADB的理由.
ABCD说明:
△ACB ≌ △ADB
这两个条件够吗?已知: 如图,AC=AD ,BC=BD. 求证: △ACB ≌ △ADB.
ABCD说明:
△ACB ≌ △ADB.
这两个条件够吗?
还要什么条件呢?议一议:已知: 如图,AC=AD ,BC=BD. 求证: △ACB ≌ △ADB.
ABCD说明:
△ACB ≌ △ADB.
这两个条件够吗?
还要什么条件呢?还要一条边议一议:已知: 如图,AC=AD ,BC=BD. 求证: △ACB ≌ △ADB.
ABCD它既是△ACB的一条边,看看线段AB
又是△ADB的一条边
△ACB 和△ADB的公共边议一议:已知: 如图,AC=AD ,BC=BD. 求证: △ACB ≌ △ADB.
ABCD证明:在△ACB 和 △ADB中 AC = A D
BC = BD
A B = A B (公共边)∴△ACB≌△ADB(SSS)议一议:应用举例? 例1:如图所示,△ABC是一个钢架,AB=AC,AD是连接点A与BC中点D的支架。
求证:△ABD≌△ACD。证明:∵D是BC的中点∴BD=CD在△ABD和△ACD中AB=ACBD=CDAD=AD∴△ABD≌△ACD(SSS)像上述判断两个三角形全等的推理过程,
叫做证明三角形全等。(SSS)
如图,在四边形ABCD中
AB=CD,AD=CB,则∠A= ∠C
请说明理由。AB=CD (已知)AD=CB (已知)BD=DB(公共边)∴ ∠A= ∠C ( )
全等三角形的对应角相等知识连接练一练 ? 工人师傅常用角尺平分一个任意角,做法如下:如图,∠AOB是一个任意角,在边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与M、N重合,过角尺顶点C的射线OC便是∠AOB的平分线。为什么?已知如图所示,AC=FE,BC=DE,AD=FB,要用“边边边”证明△ABC≌△FDE,需要那些条件?如何证明??思考 ? 例2:如图,已知AB=CD,AD=CB,求证:∠B=∠D证明:连结AC,AB=CD(已知)AC=CA(公共边)CB=AD(已知)∴ △ ABC≌ △ CDA(SSS)∴ ∠B=∠D(全等三角形对应角相等)问:此题添加辅助线,若连结BD行吗?在原有条件下,还能推出什么结论?答:∠ABC=∠ADC,AB∥CD,AD∥BC在△ABC和△ ADC中小结:四边形问题转化为三角形问题解决。经过本节课的学习,你有哪些收获?小结
